Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях

Подождите немного. Документ загружается.

∈

Ci, i = 0, n-1;

∈

Fi, i = 0, n;

Тогда вместо системы (3.32) мы должны рассмотреть систему

⎯

U = F , (3.33)

где

есть интервальная матрица, F = (F0,F1,...,Fn )т — интервальный вектор,

⎯

U — искомое

ешение. Запись (3.33) необходимо понимать так : требуется найти множество

⎯

U = { u = (u0,u1,...,un) | su = f , s

∈

S, f

∈

F},

⎯

Ui = { Priu | u

∈ ⎯

U }, i = 0,n.

Множество

⎯

U может иметь весьма замысловатую структуру. Интервально-аналитический

подход позволяет отыскать интервалы Ui такие, что

⎯

Ui Ui, i = 0,n . (3.34)

Как хорошо известно, решение системы (3.32) задается формулами

ui = xiui+1 + yi , i = n-1,n-2,...,0 (3.35)

un = yn ,

где коэффициенты xi , yi определяются соотношениями

x0 = - c0 / b0 , y0 = f0 / b0,

xi = - ci / (bi + aixi-1) , i = 1,n-1, (3.36)

yi = (fi - aiyi-1) / ( bi + aixi-1) , i = 1,n.

Покажем, что, переходя формально в формулах (3.35), (3.36) к интервалам, мы получим

интервальное решение Ui .

Тео

ема 3.6.

сть

B0 C0 0 0 0 ......................................0

A1 B1 C1 0 0 ...................................0

0 A2 B2 C2 0 ...................................0 = S

............................................................

0 .......................... 0 An-1 B n-1 C n-1

0 .......................................0 0 A n B n

Ui = XiUi+1 + Yi , i =1,n-1

, (3.37)

Un = Yn

причем

Xi , Yi

вычислены по формулам

Xi = - Ci / (Bi + AiXi-1) , i = 1,n-1

X0 = - C0 / B0

, (3.38)

Yi = (Fi - AiYi-1) / (Bi + AiXi-1) , i = 1,n

Y0 = F0 / B0

, (3.39)

в которых по предположению все выражения имеют смысл. Тогда имеет место включение

(3.34).

оказательство

Воспользуемся основной теоремой интервальной арифметики и методом

математической индукции. В силу указанной теоремы, если X0, Y0 найдены из (3.36) , то x0

X0 , y0 Y0. Предположим, что x i-1 X i-1, y i-1 Y i-1. Тогда

xi = - ci / (bi + aix i-1) - Ci / (Bi + AiXi-1) = Xi ,

yi = (fi - aiy i-1) / (bi + aix i-1) (Fi - AiYi-1)/(Bi + AiX i-1) = Yi. (3.40)

Отсюда по индукции получаем xi

∈

Xi, yi

∈

Yi при всех i ; в частности, yn = un

∈

Yn = Un.

Теперь из (3.40), (3.37), (3.35) на основании теоремы 3.4 вытекает включение ui

∈

Ui , i = n, n-

1,...,0. Так как коэффициенты ai, bi, ci, fi cистемы (3.32) произвольны, отсюда следует

справедливость (3.34).

Итак, формулы (3.37)-(3.38) дают интервальный вариант метода прогонки. Реализовать ее

можно лишь в том случае, если в соотношениях (3.38), (3.39) не встретится деление на

интервал, содержащий нуль.

3.1.7. Обращение интервальных матриц

Одним из способов решения системы уравнений (3.24)

вляется использование обратной

матрицы. Очевидно, что если нам известна матрица Т такая, что

то множество решений системы содержится в TF:

⎯

U TF.

Первый интервальный метод нахождения такой матрицы был предложен Хансеном.

Интервальная арифметика в нем используется в комбинации с априорными оценками

некоторых величин.

Выберем матрицу s*

∈

S (например, s* = m(S)) и вычислим каким-либо способом матрицу t -

приближение к *. Определим P равенством P = e - St, где e - единичная матрица.

едположим, что

<1. Тогда для любой вещественной мат

ицы

∈

P сп

аведливо

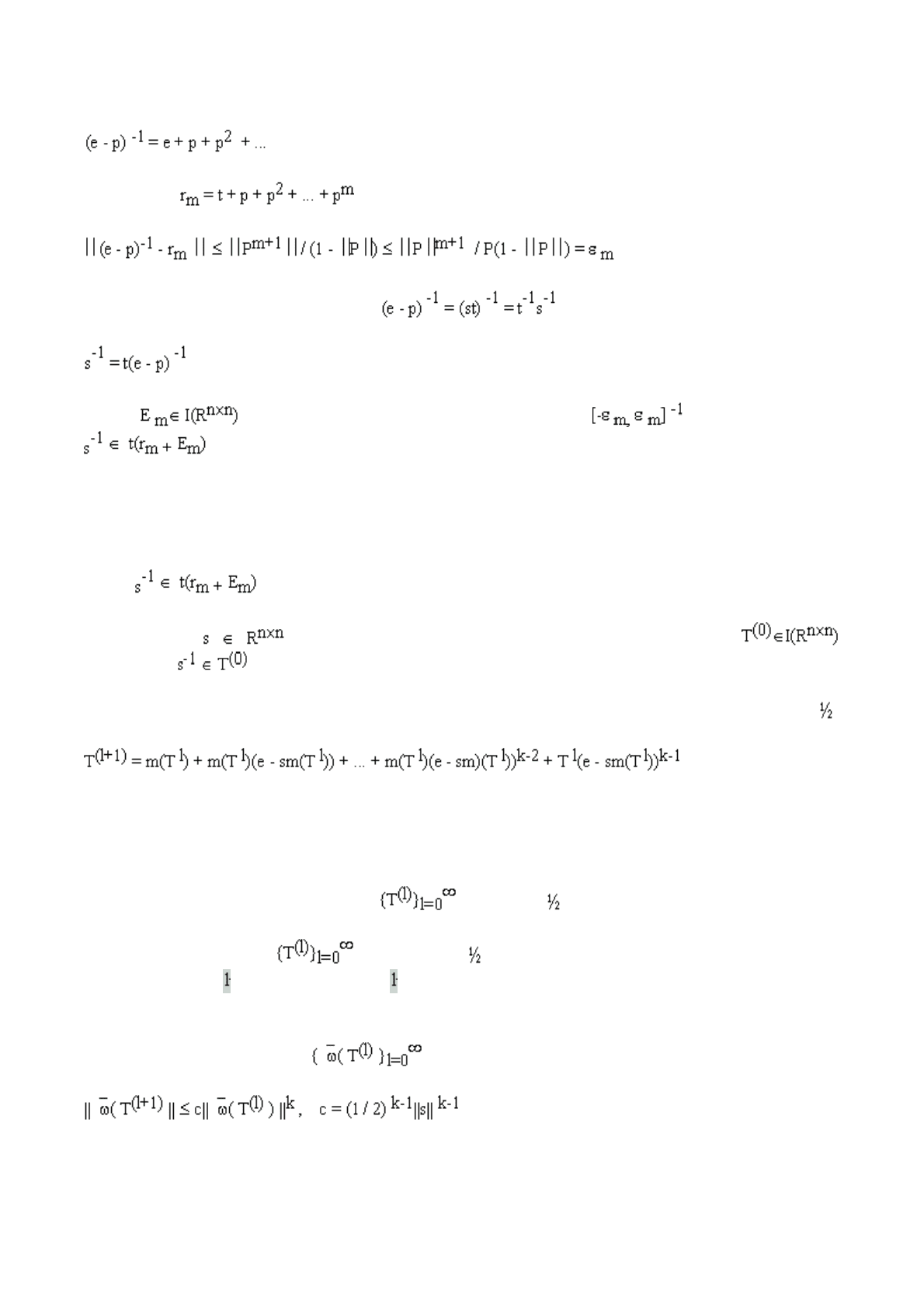
следующее представление:

Обозначим Имеет место неравенство

Если s

∈

S, то t - st = p

∈

P и, значит, , откуда

. (3.41)

Пусть - матрица, все элементы которой равны . Из (3.41) имеем

Определим интервальную матрицу Rm соотношением

Rm = ( ... ((P + e)P + e)P + ..) + e (m сложений).

Тогда для любой матрицы s

∈

Пусть теперь . - невырожденная вещественная матрица, а матрица

такова, что .

Рассмотрим итеративный процесс получения более точных интервальных приближений к s :

, k >1. (3.42)

Справедливы следующие утверждения.

Теорема 3.8 :

1. Каждый член последовательности содержит s .

2. Последовательность сходится к s тогда и только тогда, когда спектральный

адиус r(e - sm(T )) матрицы e - sm(T ) меньше единицы.

3. Если

| |.| |

монотонная мультипликативная матричная норма [312], то для

последовательности матриц выполняется оценка

где

⎯ ω

(

)

- мат

ица с элементами

(

Пусть опять s T(0) . Определим последовательность равенствами

, k >1.

. (3.43)

Теорема 3.9.

1. s T( ) при всех l = 0, 1, 2, ...

2. Последовательность сходится к s, если при всех t T( )спектральный радиус

матрицы

e - st

меньше единицы:

e - st

) <1. (3.44)

3. Если

| |

- монотонная мультипликативная матричная норма, то

Сформулируем достаточно простой критерий, когда выполняется (3.44). Пусть

такова, что s T и

| |

e - sm(T)

| |

1. Если

| | ⎯ ω

( T)

| |

< 2(1 -

| |

e - sm(T)

| |

) /

| |

, то для всех t T r(

e - st

) <1.

Для реализации методов, определяемых соотношениями (3.42), (3.43), необходимо знать

начальное приближение T(0), которое можно получить, например, интервальным методом

Гаусса. Приведем условия, достаточные для выполнения включения: s T.

Теорема 3.10.

1. Пусть матрица такова, что T(e - s) T - e. Тогда s T.

2. Если e - s - невырожденная и матрица T такова, что , то s T.

3.1.8. Интервальные итерационные методы для систем линейных

алгебраических уравнений

Применение интервальных методов гарантирует не только быструю сходимость решения за

счет обеспечения последовательного включения решений без особых затрат памяти ЭВМ, но

и возможность проверки существования и единственности решения нелинейных систем в

заданной области пространства и сходимости соответствующих итерационных процессов

[109]. Обычные вещественные итерационные методы типа метода Ньютона гарантированно

сходятся к решению лишь тогда, когда начальное приближение выбрано достаточно близко к

нему [109].

Пусть система линейных алгебраических уравнений записана в виде

x = a x + b

(

3.45

)

, причем относительно а и b известно , что a A, b B,

В качестве примера интервальных итерационных методов для (3.45) рассмотрим метод

простой итерации

Теорема 3.11.

Итерации

, k 0 , (3.46)

cходятся к единственной неподвижной точке уравнения

X = A X + B

при любом начальном тогда и только тогда, когда

r ( |A| ) < 1.

оказательство

Достаточность.

Прежде всего заметим, что

⎯

Далее, поскольку r ( |A| ) < 1 и |A| 0 (0- нулевой элемент из ), то существует и

Отсюда для произвольных k и m 1 получаем

Поскольку , последовательность

{X(k)}

является последовательностью Коши и,

значит, , откуда

X*=AX*+B

. Единственность X* следует из того, что

еобходимость

Пусть итерации , сходятся к X* при любом начальном

. Покажем, что r (|A|) < 1. Согласно теореме Перрона - Фробениуса вещественная

неотрицательная матрица |A| = (|Aij|) имеет неотрицательный собственный вектор,

соответствующий собственному значению

= r ( |A| ).

Из сходимости X(k) к X*при произвольном X(0) следует сходимость к

⎯ ω

(X*).

Выберем X (0) так, чтобы

⎯ ω

(X(0)) являлся собственным вектором |A|, соответствующим

r ( |A| ), и по крайней мере один из

компонентов

⎯ ω

(X(0)) был больше соответствующего

компонента

(

)

. Тогд

, п

едположив r

(

)

1, пол

чим

Переходя к пределу, имеем

⎯ ω

(X*)

⎯ ω

(X(0)), что противоречит выбору X (0). Теорема

доказана.

Нетрудно показать, что

⎯

. Кроме того Х*, оптимально в

следующем смысле: не существует интервального вектора такого, что

. В самом деле, из равенства X* = AX* + B следует, что

где

т.е. . Другими словами, х

⎯

х* { х|х=ах+b, a

A, b B}.

Если мы начинаем итерации по формуле (3.46) при произвольном , то несмотря на

авенство , нет гарантии, что X* , а значит, и того, что

⎯

X .

С другой стороны, такая гарантия будет , если выбран с условием X* .

Действительно, из монотонности по включению тогда следует, что

и по индукции X* и X* + B, а значит,

Отсюда вытекает видоизменение алгоритма (3.46). Выберем такое, что X* , и

положим

Из сказанного ранее следует, что X* при всех k = 1,2,... Если вычисления ведутся в

машиной интервальной арифметике, то эта последовательность сходится за конечное число

шагов, т.е. начиная с некото

ого , так что выполнение

авенства

может служить естественным критерием прекращения итераций.

Еще один подход к пострoению итерационных методов для системы (3.24) состоит в

следующем. Умножим обе части этого уравнения на невырожденную матрицу Y. Например,

и положим T = e - Ys. Если ||T||<1, то возьмем вектор такой, что

⎯

, и определим последовательность

. (3.47)

Справедлива следующая теорема.

Теорема 3.12.

Если для некоторой матрицы

справедливо неравенство

||e - Ys|| 1,

то, каковы бы ни были

s S, f F,

система имеет единственное решение и при любом

k 0

это решение содержится в интервальном векторе

U(k)

, найденном с помощью (3.47).

В качестве U(0) можно взять, например, вектор с компонентами

Как видно из библиографии [276] и работы [104] подавляющее большинство публикаций по

линейной алгебре в интервальном анализе посвящено исследованию вопроса о решении

системы интервальных уравнений

(3.48)

где , , - множества интервальных

матриц,

-векторов и чисел соответственно.

В интервальном анализе ищут обычно, так называемое,

поточечное решение

[271] системы

интервальных уравнений (3.48), т.е. множество

Такое понятие поточечного решения не удовлетворяет сложившейся концепции решения

уравнения, т.е. подстановка найденного

в (3.48) не дает равенства левой и правой частей

уравнений. Соответствующее этой концепции решение названо в [103] алгебраическим

интервальным решением , причем . Алгоритм получения этих решений подробно

изложен в [103].

Существуют также стандартные пакеты прикладных программ по решению систем уравнений

с интервальными матрицами коэффициентов [190]. Для линейной системы уравнений

существует интервальный аналог метода Ньютона-Гаусса-Зейделя (IGS) [325]. Этот

метод требует незначительных затрат по памяти и времени на каждом шаге, но может

медленно сходиться.

Симметрические методы [325] имеют более высокую скорость сходимости чем IGS. Эти

методы используют частичную упорядоченность на . Сходимость этих

методов доказывается с помощью интервальной арифметики с использованием теоремы о

включении [304].

Существует также целый ряд методов, основанных на использовании обратной матрицы .

Алефельдом и Херцбергером предложен итеративный процесс получения более точных

интервальных приближений к обратной матрице [109]. Множество решений

может состоять из одного или нескольких интервалов. В этом случае

указанный выше метод применяется для каждого из этих интервалов отдельно [109].

При наличии в задаче точных исходных данных интервальный анализ позволяет обеспечить

порождение границ и сходимость к решению при сравнительно слабых предложениях [8]. Не

обязательным для решения систем линейных алгебраических уравнений является и

требование, чтобы начальное приближение содержало в себе множество решений

линейной системы. В [109]описаны методы Румпа и Гея, для которых это включение

достигается в ходе итераций.

Современные методы интервального анализа кроме основных арифметических операций над

интервальными величинами содержат развитые средства для решения систем линейных и

нелинейных уравнений, методы решения дифференциальных уравнений и т.д. [48, 109, 247,

304, 323].

Целью интервального анализа при решении дифференциальных уравнений является

получение строгих верхних и нижних границ решения по заданным границам (интервалам)

исходных данных (начальных и граничных значений, коэффициентов уравнений и т.п.) [304].

Эти методы применимы для решения линейных и нелинейных обыкновенных

дифференциальных уравнений в частных производных [247, 304] и являются более

надежными, строгими и простыми по сравнению с классическими методами решения

дифференциальных уравнений. Кроме того, в них автоматически учитывается неточность,

связанная с ошибками округления ЭВМ.

Использование понятия интервальных ограничений и кода Hensel дало возможность [283]

создать специальные методы для ЭВМ, свободные от ошибок округления и применить их для

ешения целого ряда приложений (решение систем линейных уравнений, интервального

линейного программирования и т.д.). Наиболее подробная библиография работ по

интервальной математике (около 1700 работ) содержится в обзоре [276].

Общим недостатком применения интервальных методов является наличие в некоторых

случаях слишком широких интервальных оценок результата, что не всегда приемлемо для

проведения практических расчетов.

3.2. Особенности решения нечетких и интервальных

уравнений

Многие расчетные и оптимизационные задачи в условиях неопределенности приводят к

необходимости решения уравнений с нечеткими или интервальными коэффициентами и

переменными. К особенностям нечеткой и интервальной алгебры следует отнести нарушение

закона дистрибутивности

и кроме того .

Эти особенности создают значительные трудности при решении

-уравнений, поскольку их

нельзя упростить путем эквивалентных преобразований. В ряде работ предлагаются методы

частичного решения этой проблемы: "дополнительные" операции в [7], использование

квазилинейного пространства [247], мнимые интервалы [243], нестандартные вычитание и

деление [109], обобщенная и сегментная интервальные арифметики [109].

Одним из возможных путей решения этой

проблемы является введение понятия мнимого

интервала. В силу следствия теоремы 2.8 все определения вводятся для интервалов

вещественной оси, т.е. для пространства

I(R)

с интервальными операциями.

Если интервал , то

сопряженным интервалом

по отношению к

называют

мнимый интервал

. Множество мнимых интервалов

обозначим через

I*(R)

. Для перехода к сопряженному интервалу справедливы

следующие соотношения:

Алгебраические операции над сопряженными интервалами определяются следующим

образом [243]. Если то, согласно (2.76):

Тогда для сопряженных интервалов , вводятся

следующие соотношения:

Например, если , то .

Следовательно, , и .

С использованием введенных понятий решение линейного уравнения

записывается в виде . Для уравнения получаем .

Решениями таких уравнений могут быть и мнимые интервальные величины. В общем случае

ешение линейного уравнения

(3.49)

имеет вид .

Можно также показать, что если , то при замене нескольких или всех

полученный результат .

Рассмотрим следующее обобщение для решения нечетких уравнений с использованием

понятий сопряженного интервала и интервально-значного нечеткого множества.

Интервально-значное нечеткое множество

(

i-v

нечеткое множество)

, определенное на

множестве

, задается в виде [281]:

Интервально-значную функцию принадлежности можно записать в виде

Пример интервально-значной функции принадлежности приведен на рис. 3.4. Различные

операции с

i-v

нечеткими множествами могут выполняться аналогично соответствующим

операциям нечетких множеств для нижних и верхних граничных

функций принадлежности [149].

Обобщение для решения нечетких линейных уравнений типа (3.49) состоит в том, что для

каждого

-уровня исходных

-функций находится интервальное решение с помощью

обычной интервальной арифметики и решение с использованием сопряженных

интервалов. Таким образом, решение нечеткого уравнения получаем в виде интервально-

значной функции принадлежности .

Пример 3.11.

Рассмотрим решение уравнения . Пусть коэффициенты уравнения заданы

треугольными

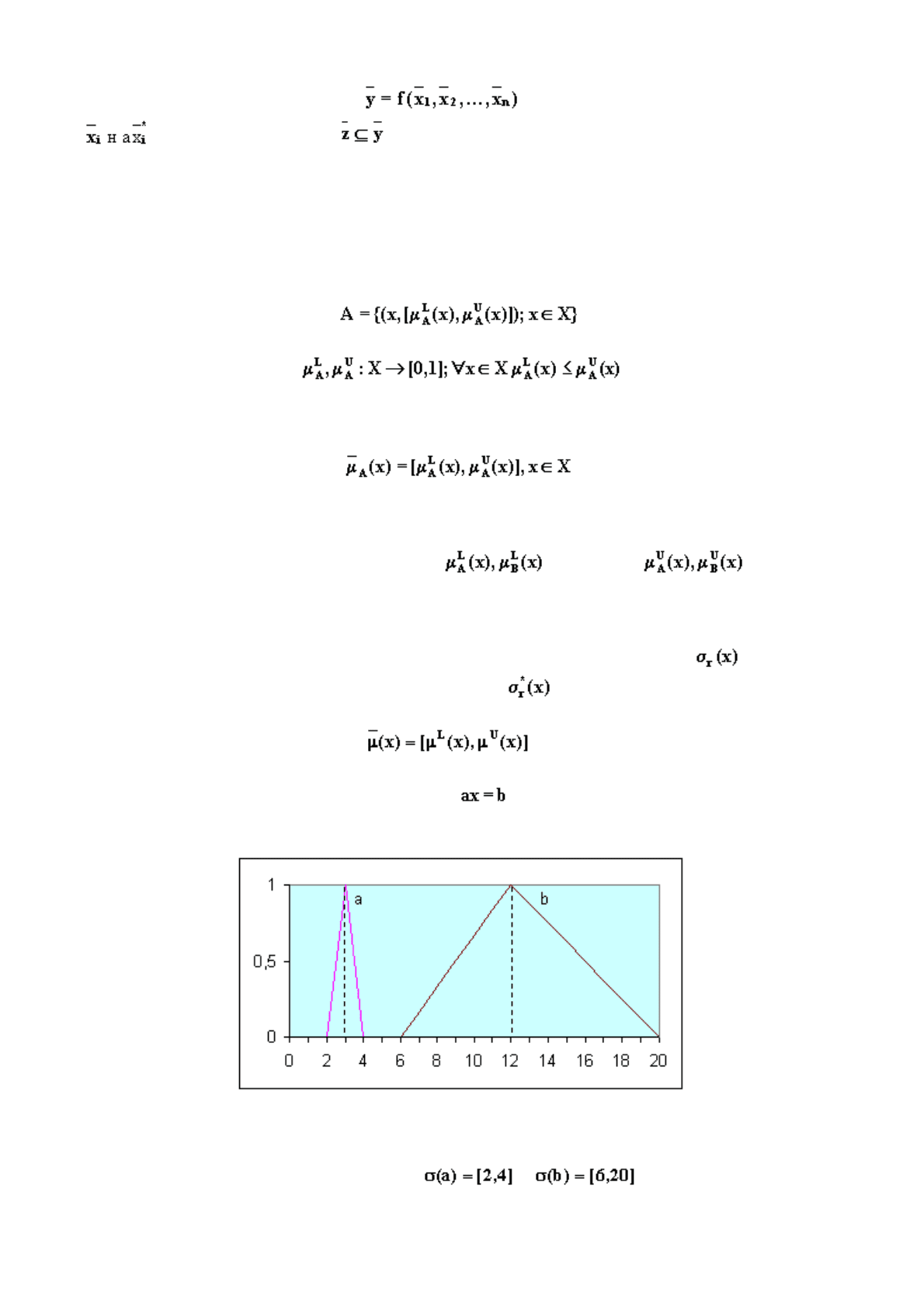
-функциями (рис. 3.3).

Рис 3.3.

Для носителей исходных

-множеств , находим интервальное

ешение