Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях
Подождите немного. Документ загружается.


.
Этот же результат был получен прямым методом в примере 2.17.
Рассмотренные аналитические методы построения функции принадлежности позволяют
получить результат операции сразу в аналитическом виде, что очень удобно для практических
приложений. Однако на практике могут встречаться более сложные аналитические
выражения для исходных
F
-величин, для которых имеются значительные трудности при
нахождении аналитического решения. К тому же, иногда возникает необходимость в
численных методах работы с дискретно заданными
F
-функциями. В этом случае
F
-
величина
A
°
B
также будет дискретной. Для практических приложений этого, как правило,
вполне достаточно. При необходимости полученное решение можно аппроксимировать
некоторой функциональной зависимостью.
2.6. Численные методы для операций с F- величинами
Будем рассматривать те
F
-величины из , для которых
F
-функция достигает на носителе
своей верхней грани.
Прямой метод
Для
F
-величин
при заданном числовом значении
z
0
, найти величину , определяемую соотношением
(2.3). Если
°
- есть операция деления, то
0 [c, d]
. Обозначим
l= min(a
°
c, b
°
c, a
°
d, b
°
d), m= max(a
°
c, b
°
c, a
°
d, b
°
d).
Тогда , т.е. достаточно рассматривать
z
0
из
[l, m]
. С помощью замены
переменных из уравнения связи (2.3) сводится к одномерной экстремальной задаче.
Рассмотрим каждую операцию в отдельности.
Сложение.
Уравнение связи имеет вид
x+y=z
0
,
т.е. одномерная задача записывается следующим образом
(2.60)
Поскольку откуда то получаем
(2.61)
В
ычитание.
С учетом уравнения связи
x-y=z
0
, одномерная задача запишется в виде
(
2.62
)

Из неравенств получаем, что (2.63)
Д
елени
е
.
С учетом уравнения связи
x/y=z
0
, одномерная задача запишется в виде
(2.64)
Поскольку
y [c, d]
, то
c x/z
0
d
. Отсюда, если
z
0
0
, то
z
0
c x z
0
d
и, если
z
0
<
0
, то
z
0
d
xc
. Окончательно, с учетом неравенства получаем:
если
z
0
0
, то (2.65)
если
z
0
<
0
, то (2.66)
Умножение.
С учетом уравнения связи
xy=z
0
, одномерная задача запишется в виде
(2.67)
Поскольку
y [c, d]
, то
cz
0
/x d
. Воспользуемся следующими свойствами неравенств: если
0<m n
или
mn<0
, то
1/m 1/n
. Рассмотрим два случая.
1. Пусть
B
или
B
. Тогда
1/d x/z
0
1/c
. Если
z
0
0
, то
z
0
/d x z
0
/c
, а если
z
0
<0
, то
z
0
/c xz
0
/d
. C учетом неравенства получаем:
(2.68)
(2.69)
2. Пусть
0 [c, d]
. Если
x 0
, то
xc z
0
,
xd z
0
или, с учетом знаков величин
c
и
d
, получим:
x z
0
/c
,
x z
0
/d
. Следовательно, если
z
0
0
, то
x z
0
/d
, а если
z
0
<0
, то
x z
0
/c
.
Аналогично, при
x<0
получим: если
z
0
0
, то
xz
0
/с
, а если
z
0
<0
, то
x z
0
/d
. Окончательно,
с учетом неравенства имеем:
(2.70)
(2.71)
Если, например,
A
, то
(2.72)
(
2.73
)

В практических приложениях чаще всего
A,B
. В этом случае множество
U
определяется по (2.68).
Пусть , где - зависимость, полученная из уравнения
связи . Для операции умножения установлено, что если
0 (a, b)
и
0 (c, d)
, то
F
-
величина
AB(z
0
)
с функцией принадлежности может быть невыпуклой,
но являться объединением выпуклых
F
-величин.
Пример 2.36
.
Пусть , . Тогд
а
.
Например, и
- невыпуклая, но является объединением выпуклых
F
-величин.
Методы решения одномерных экстремальных задач достаточно подробно освещены в
специальной литературе [41, 71, 163, 233], поэтому мы не будем касаться этого вопроса.
Обратный метод
Обратный численный метод нахождения результатов алгебраических операций первого типа
для
F
-величин из основывается на следствии теоремы 2.8, т.е. на соотношении
(2.57).
Пусть Зададим, например, равномерное разбиение отрезка
[0,
α Υ β
]
:
(2.74)
Тогда из решения уравнений
(2.75)
получим
отк
у
да

(2.76)
Таким образом, получаем дискретное представление
F
-величины
C
:
(2.77)
где значение принадлежит исходному разбиению (2.74).
Эффективность реализации данного метода во многом определяется возможностью решения
уравнений (2.75). Можно предложить следующий подход. Выбирается некоторый базовый
набор
F
-величин, для которых уравнения (2.75) решаются достаточно просто (аналитически
или численно). Кроме того, необходимо, чтобы с помощью теоретико-множественных
операций над элементами данного набора можно было бы с достаточной точностью
представить широкий класс
F
-величин. При этом важную роль в реализации данного подхода
играет принцип декомпозиции. Обратный численный метод является наиболее удобным из
всех алгебраических и численных методов, приведенных выше.
Матричные методы
Для решения характерных для практики задач большой размерности необходимо
использовать методы, обеспечивающие высокую скорость решения задач оперативного
контроля и управления в реальном масштабе времени. Такие методы могут быть созданы на
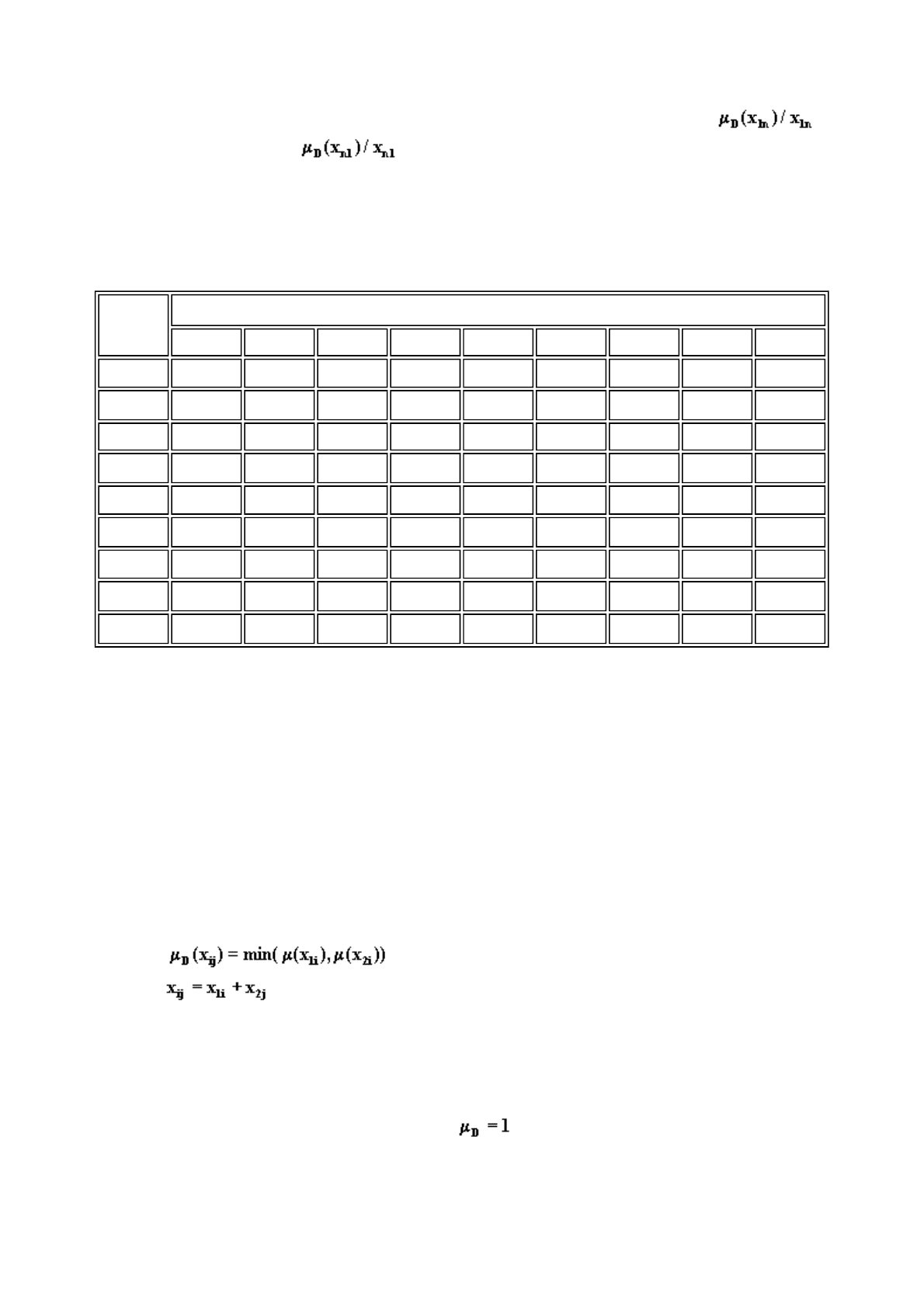
основе учета особенностей структуры элементов - матрицы, представляющей из себя
р
езультирующую матрицу для операции сложения в условиях, когда функция
принадлежности представлена
l
нечеткими дискретизированными величинами вида
.
Пример такой матрицы для
l = 2
приведен в таблице 2.1.
Исходные функции принадлежности располагаются в левом столбце и верхней строке
матрицы. Элементами этой матрицы являются дискретные нечеткие величины
, где ; .
Эта матрица получена для равномерной дискретизации по
х
. Анализ структуры этой матрицы
позволил разработать для операции сложения метод построения результирующей функции
принадлежности. Этот метод применим для выпуклых функций принадлежности, и в
р
езультате операции получается также выпуклая результирующая функция (теорема 2.7).
Программа построения результата операции сложения для
l
- функций принадлежности
приведена в [39]. Процедура построения результирующей функции начинается с элемента
и заканчивается элементом . Для элемента проводится
анализ соседних с ним элементов и и выбирается
р
ез
у
льти
ру
ющий элемент имеющий максимальное значение
фу
нкции п
р
инадлежности. Далее
процедура повторяется для вновь выбранного элемента. Для операции вычитания также
может быть применен этот алгоритм, но начинается он с элемента и
заканчивается элементом , соответственно изменяется и процедура изменения
индексов для определения соседних элементов. Однако построить аналогичные алгоритмы
поиска решений для операций умножения и деления в общем случае не удается.
Таблица 2.1.
Матрица принятия решения для двух подсистем
В результате проведенного анализа структуры результирующей матрицы было выяснено, что
она не содержит в полном объеме информации, необходимой для достаточно точного
построения результирующей дискретизированной функции принадлежности для всех
операций.
Поэтому был разработан новый матричный метод, применимый ко всем арифметическим
операциям. Он основан на дискретизации не по парамеру х, а по значениям функции
принадлежности - по r-уровням.
Пример матрицы с такой дискретизацией приведен в табл. 2.2.
В этой матрице две исходные функции принадлежности размещены также как и раньше - в
левом столбце и верхней строке. В каждой клетке матрицы в числителе записан результат
операции . В знаменателе размещены результаты для операции
сложения .
p
>p>Для выпуклых функций принадлежности, изменяющихся на носителе от 0 до 1,
р
езультирующая матрица имеет очень интересную структуру. В этой матрице четко
выделяются так называемые
иннеры
[346] - концентрические внутренние квадратные
подматрицы с одинаковым для всей подматрицы значением функции принадлежности.
Первый иннер есть одноэлементная матрица с , т.е. скаляр.
μ
D
(x
ij
)
μ
D
(x
ij
)
0,046/160 0,109/165 0,248/170 0,500/175 0,850/180 0,937/185 0,842/190 0,390/195 0,102/200
0,000/60 0,000/220 0,000/225 0,000/230 0,000/235 0,000/240 0,000/245 0,000/250 0,000/255 0,000/260
0,015/65 0,015/225 0,015/230 0.015/235 0,015/240 0,015/245 0,015/250 0,015/255 0,015/260 0,015/265
0,047/70 0.046/230 0,047/235 0,047/240 0,047/245 0^047/250 0,047/255 0,047/260 0,047/265 0,047/270
0,078/75 0,046/235 0,078/240 0,078/245 0,078/250 0,078/255 0.078/260 0,078/265 0,078/270 0,078/275
0,125/80 0,046/240 0.109/245 0,125/250 0,125/255 0,125/260 0,125/265 0,125/270 0,125/275 0,102/280
0,234/85 0,046/245 0,109/250 0,234/255 0,234/260 0,234/265 0.234/270 0,234/270 6,234/280 0,102/285
0,492/90 0,046/250 0,109/255 0,248/260 0,492/265 0,492/270 0,492/275 0,492/280 0,390/285 0.102/290
0.859/95 0,046/255 0,109/260 0,248/265 0,500/270 0,850/275 0,859/280 0,842/285 0,390/290 0,102/295
0,625/100 0,046/260 0,109/265 0,248/270 0,500/275 0,625/280 0,625/285 0,625/290 0,390/295 0,102/300

Таблица 2.2.
Учитывая следствие теоремы 2.8, а также особенности интервальных операций (2.76), можно
легко показать, что решения для результирующей функции располагаются в зависимости от
вида операции на одной из диагоналей матрицы: для сложения и умножения на диагонали А,
которая проходит из левого верхнего угла в правый нижний угол, для вычитания и деления -
на
другой диагонали В. В алгоритме рассмотрены также и все возможные варианты - наличие
отрицательных нечетких величин, принадлежность 0 к носителям нечетких величин и т.д.
Интересно также отметить, что на диагоналях можно получить не только поточечные, но и
алгебраические решения [103], т.е. такие функции принадлежности, которые при подстановке
в исходное уравнение позволяют
обеспечить равенство левой и правой части, а не только
включение. Так, например, для операции деления поточечное решение лежит на диагонали В,
а алгебраическое - на диагонали А. Этот факт полностью соответствует специальным
дополнительным операциям вводимым в интервальном анализе [247] и теории нечетких
множеств.
Для реализации нечетких алгоритмов можно с успехом использовать пакеты программ и
ЭВМ, в которых реализована интервальная арифметика, что связано с возможностью
представления
F
-величин через совокупность ее
r
-уровней и на следствии теоремы 2.8.
Методы расчета с применением интервальной арифметики в настоящее время развиваются
очень интенсивно [8, 48, 247, 276, 304, 323, 324]. Уже существуют ЭВМ, в которых
интервальная арифметика реализована аппаратно или микропрограммно [324], а для
универсальных ЭВМ разработан целый ряд пакетов программ для нечетких и интервальных
величин FUZZY, FUZZYC, ФСТДС, FAGOL, ЛПЛ, ACFITH, PASCAL-SC [6, 247, 304, 324].

Первые два пакета позволяют работать лишь с дискретными нечеткими величинами. Для
проведения нечетких теоретико-множественных операций можно также использовать систему
FSTDS (Fuzzy Sets Theoretic Data Structured), FLOU (Fuzzy Language of Osaca University) [8].
Основная сложность при работе с нечеткими величинами заключается в том, что даже в
случае простейших исходных функций принадлежности в результате элементарных операций
над ними получаются функции принадлежности сложной формы, требующие для своего
описания большого числа параметров. Поэтому во многих работах [65, 98, 265, 266, 268]
предлагается аппроксимировать исходные функции принадлежности и результаты операций
над ними определенным классом функций, зависящих от фиксированного числа параметров:
треугольных, экспоненциальных, трапециевидных и т.д. В этом случае имеется возможность
построения сравнительно простых основных операций, не выводящих за пределы избранного
класса функций [265].
Нечеткое число LR-типа
. Нечеткое число называется нечетким числом
LR
-типа или
LR
-
числом [266, 267, 268], если
где
L
и
R
- две непрерывные неотрицательные функции: ; , где
R
-
вещественная ось со следующими свойствами:
1. , .
2. , .
3.
L, R
не возрастают на
[0, + ]
.
4. , .
Таким образом, нечеткое число
LR
-типа характеризуется видом функций
L
и
R
, а также
тремя параметрами и может быть записано как .
Для нечетких
LR
-чисел арифметические операции записываются гораздо проще [268]:
;
;
;
;
;
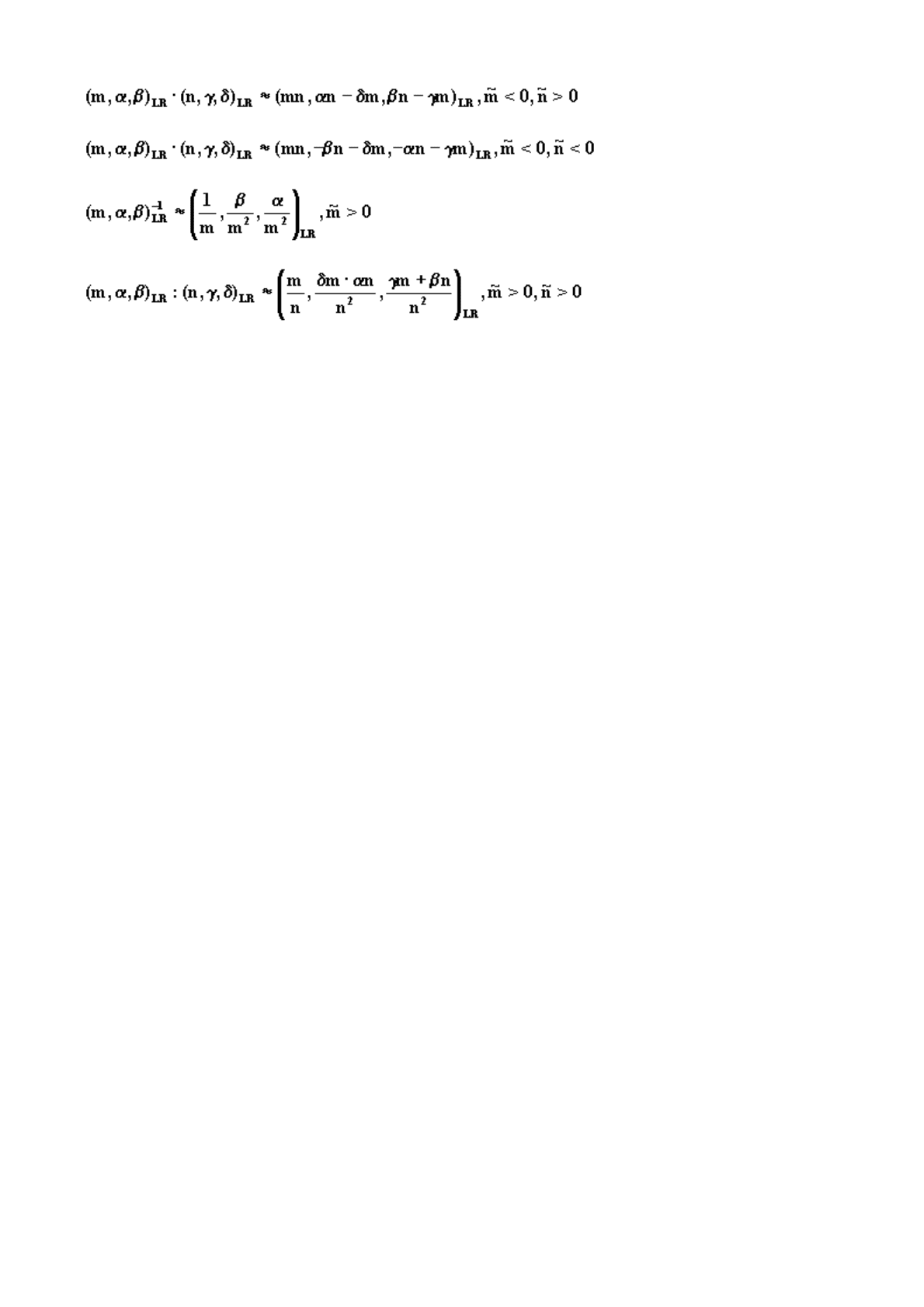
;
;
;
.
Формулы для операций умножения и деления зависят от знаков операндов, при этом носители
обоих операторов не должны содержать ноль.
Анализ влияния степени и вида нечеткости параметров для нескольких типов функций
принадлежности для представления нечетких чисел на чувствительность целевой функции
оптимизации проведен в работе [312]. Попытки создания универсальных высоко
транспортабельных структурированных пакетов программ для выполнения интервальных
вычислений на базе предпроцессора AUGMENT привели к резкому увеличению времени
выполнения операций по сравнению с традиционными (неинтервальными) вычислениями на
тех же примитивных объектах (числах с плавающей точкой фиксированной разрядности) в
зависимости от различных условий в 50-200 раз [8]. Наибольшая эффективность достигнута в
экспериментах с микропрограммным способом интерпретации для процессора РDР -11/40Е,
что позволило уменьшить коэффициент замедления до 1,8. В 1985 году в США принят
стандарт Р754 по вопросам реализации интервальных вычислений, который в настоящее
время практически стал международным. По этому стандарту работают, например,
микропроцессоры INTEL - 8087 (фирма INTEL), МС 68881 (фирма Motorola), WE 32106
(разработка BELL Labs) и т.д. [8].
Оригинальное расширение стандартного языка программирования для возможности работы с
нечеткими величинами путем введения переменных типа FUZZY приведено в работе [65].
Я
зык FAGOL позволяет оперировать с нечеткими величинами при аппроксимации их
F
-
функций треугольными функциями принадлежности.
Ведутся также работы по созданию лингвистических терминальных комплексов, состоящих
из универсальных микропроцессоров; ОЗУ, спецпроцессоров, ориентированных на
выполнение операций над нечеткими множествами; ПЗУ-термов, предназначенных для
хранения первичных терм-значений лингвистических переменных и других устройств [152].
Однако все эти методы используют аппроксимацию результирующих функций
принадлежности определенным классом функций, что ведет к потере информации и
у
величению области неоп
р
еделенности.

ГЛАВА 3. ОСОБЕННОСТИ РЕШЕНИЯ
НЕЧЕТКИХ И ИНТЕРВАЛЬНЫХ
УРАВНЕНИЙ
3.1. Анализ интервальных методов
При управлении различными технологическими процессами необходимо обеспечить в
р
еальном масштабе времени расчет и оптимизацию режима, который гарантированно будет
лежать в области допустимых режимов и будет реализуем системами автоматического
управления нижнего уровня иерархической системы управления. Стандартно применяемые
методы мало подходят для решения задач такого класса ввиду низких скоростей сходимости
вещественных итерационных методов типа метода Ньютона и возможности появления
произвольных неконтролируемых ошибок в результатах при наличии погрешностей в
исходных данных. Кроме того, в зависимости от имеющегося вида неопределенности при
принятии решений необходимо обеспечить проведение на ЭВМ расчетов с интервальными и
нечеткими величинами.
Например, особенности управления системами газоснабжения заключаются в том, что даже
р
едкие колебания давлений и расходов сверх определенных пределов (прежде всего
прочностных) могут привести к авариям. Поэтому при управлении такими системами
приходится ориентироваться на самое неблагоприятное (экстремальное) сочетание факторов
неопределенности и использовать понятие гарантированного результата [116, 137].
Наиболее перспективными для нахождения решений систем уравнений с учетом отмеченных
особенностей работы алгоритмов реального времени в условиях неопределенности являются
интервальные [109, 175, 277, 304, 323] и нечеткие [2, 166] методы. Эти методы получили
большое распространение при решении систем дифференциальных уравнений [109, 247, 304],
систем линейных и нелинейных уравнений [109, 175, 232, 234], задач глобальной
оптимизации [323].
Применение интервального анализа и различных минимаксных (гарантированных) подходов
[48, 49, 116, 133, 242, 304] обладает целым рядом преимуществ:
- не требуется знание вероятностных характеристик неопределенных факторов, которые
р
едко бывают точно известны на практике;
- при минимаксном подходе получают строгие оценки для самих искомых величин, а не для
вероятностей или математических ожиданий, что имеет большое значение при наличии
малого числа замеров параметров и одной или нескольких реализаций;
- cтатистические характеристики не могут гарантировать определенный исход одного
конкретного опыта;
- во всех случаях даются гарантированные двусторонние аппроксимации искомых решений.
При минимаксном подходе операции над неопределенными величинами сводятся к
соответствующим операциям над областями, однако даже в случае простых исходных
областей неопределенности в результате операций над ними получаются области сложной
формы, требующие для своего описания большого числа параметров [242]. Поэтому на
п
р
актике п
р
именяется апп
р
оксимация области неоп
р
еделенности классом областей,

зависящим от фиксированного числа параметров: параллелепипедами [247], эллипсоидами
[50, 242] и т.д. Ставятся и задачи минимизации объема результирующих областей
неопределенности [242].
В общем случае точность интервального результата полностью определяется следующими
четырьмя факторами [8]:
1. Неопределенностью в задании исходных данных.
2. Округлениями при выполнении операций, изменяющих или порождающих интервальные
объекты.
3. Приближенным характером используемого численного метода.
4. Степенью учета зависимостей между участвующими в вычислении интервальными
объектами (переменными и константами).
Увеличение точности расчетов (уменьшение ширины результирующего интервала)
достигается за счет компенсации влияния этих факторов. Задача получения для данного
множества машинно-представимых чисел самого узкого интервала, содержащего
объединенное расширение соответствующей рациональной функции, может ставиться как
оптимизационная.
Для уменьшения погрешности округления используются изменение разрядности чисел,
р
азличные способы машинного представления и специальное упорядочение цепочки
следующих друг за другом операций. А компенсация влияния четвертого фактора
осуществляется путем предварительной обработки исходного алгоритма, в процессе
вычислений и апостериорно [8].
Как отмечается в Добавлении А.Г.Яковлева к [8] широкое распространение интервальной
арифметики обусловлено фактическим отсутствием конкурентноспособных подходов к
построению надежного (в смысле гарантированности) и транспортабельности (по
включению) программного продукта для решения численных задач. Интервальный подход
позволяет навести математическую строгость в построении численных алгоритмов, которые
традиционно основывались на аппроксимации точного значения одним "достаточно близким"
к нему приближением. Для интервальных методов даются гарантированные двусторонние
аппроксимации искомых решений [48], имеющие смысл наихудшего случая с точки зрения
описания неопределенностей [249].
В связи с важностью понятий интервального анализа для теории нечетких множеств приведем
основные понятия и методы из [109].
3.1.1. Интервальная арифметика
Интервальные числа
Пусть – множество всех вещественных чисел. Под
интервалом
, всюду ниже,
если не оговорено противное, понимается замкнутое ограниченное подмножество вида
.
Множество всех инте
р
валов обозначим че
р
ез . Элементы б
у
дем записывать
