Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях

Подождите немного. Документ загружается.

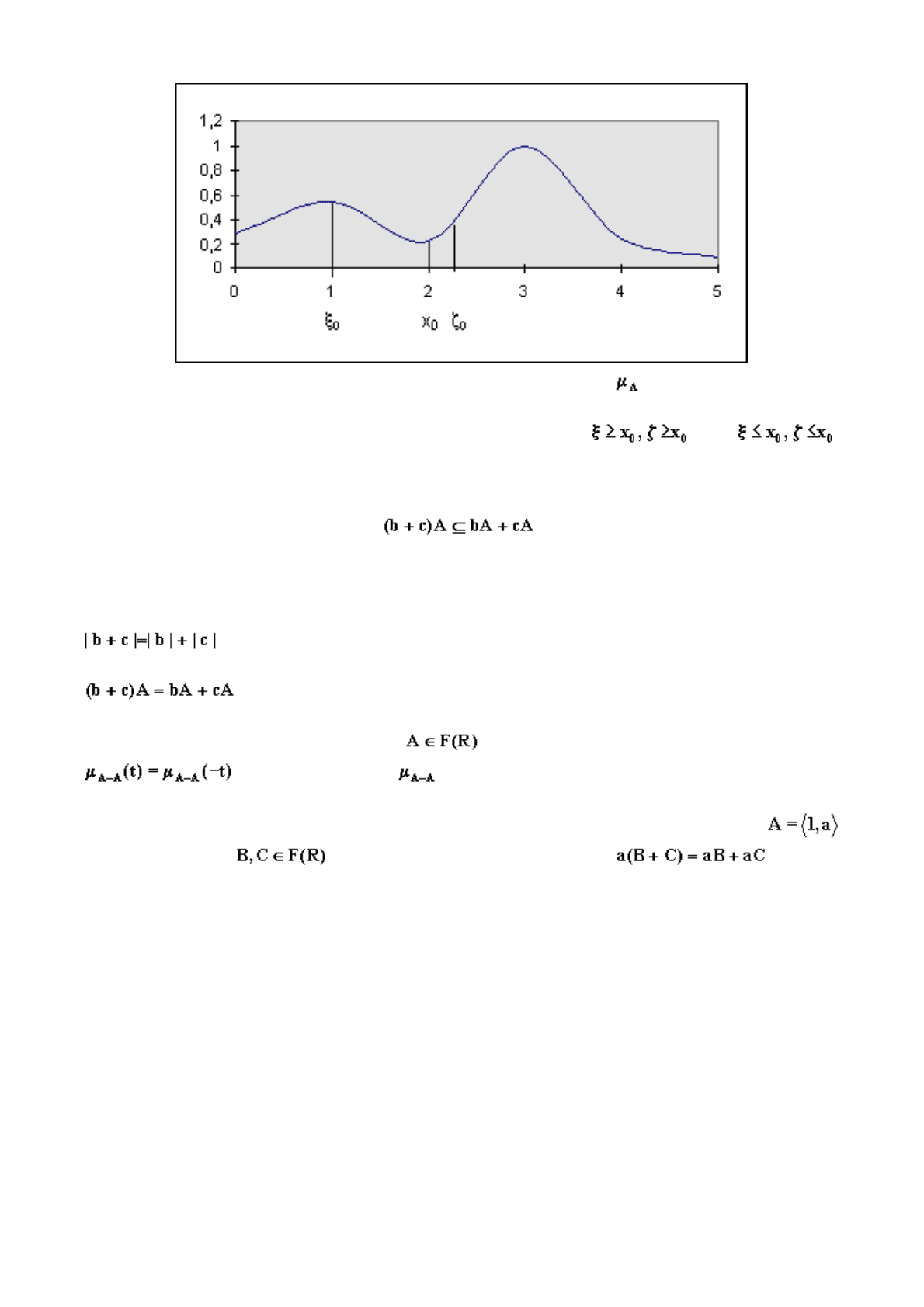
Рис.2.3. График для невыпуклой функции .

2. Пусть

разных знаков. Тогда из (2.16) следует, что или .

Проведя соответствующий анализ, нетрудно убедиться, что независимо от выпуклости

величины

выполняется соотношение

Таким образом, справедлива следующая теорема.

Теорема 2.5.

Если

- выпуклая

-величина и

такие вещественные числа, что

, то выполняется равенство

. (2.17)

Далее, из (2.15) для произвольной получаем следующее очевидное свойство

, (2.18) т.е. функция симметрична относительно нуля.

Последнее свойство, которое отметим в данном разделе, заключается в том, что при

для произвольных из (2.11) и (2.12) следует равенство . (2.19)

2.3. Алгебраические системы F-величин

Из определения алгебраических операций над

-величинами видно, что равенство

A-B=0

справедливо тогда и только тогда, когда

A=B=(1, a)

. Следовательно,

-величина не имеет

обратного элемента относительно сложения. Нетрудно показать, что аналогичное

утверждение справедливо и для операции умножения. Таким образом, в

F(R)

вычитание

необратно сложению, а деление необратно умножению. Учитывая дополнительно

коммутативность и ассоциативность сложения и умножения заключаем, что

F(R)

относительно каждой из данных операций образует абелеву (коммутативную) полугруппу и,

следовательно, не является полем.

Попытка классификации

F(R)

как векторного (линейного) пространства над

не приводит к

успеху в силу отмеченной выше особенности операции сложения и полученного в

едыд

щем

азделе ог

аничения на выполнения

авенства

Воспользуемся следующим понятием, введенным в интервальном анализе [247].

белева пол

гр

ппа

относительно сложения с нейтральным называется квазилинейным

пространством над полем

, если для любых и справедливы следующие

соотношения:

1. ;

2. , если ;

3. ;

4. ;

5. ;

6. .

сно, что класс

F(R)

в целом не является квазилинейным пространством, поскольку второй

пункт определения, как указывает теорема 2.5, выполняется только для выпуклых

-величин.

При этом дополнительном условии проанализируем выполнение двух последних пунктов

определения, поскольку справедливость оставшихся доказана или очевидна.

Пусть и . Тогда из (2.3) следует, что . Это значит, что

если потребовать единственность элемента , то первые пять пунктов определения для

подкласса выпуклых F-величин, которые обозначим через , с условием

Следующая теорема устанавливает критерий выполнения шестого пункта определения для

величин из .

Теорема 2.6.

Пусть и выполняются условия:

1. ;

2. ;

3. для каждой указанной пары и выполняются неравенства:

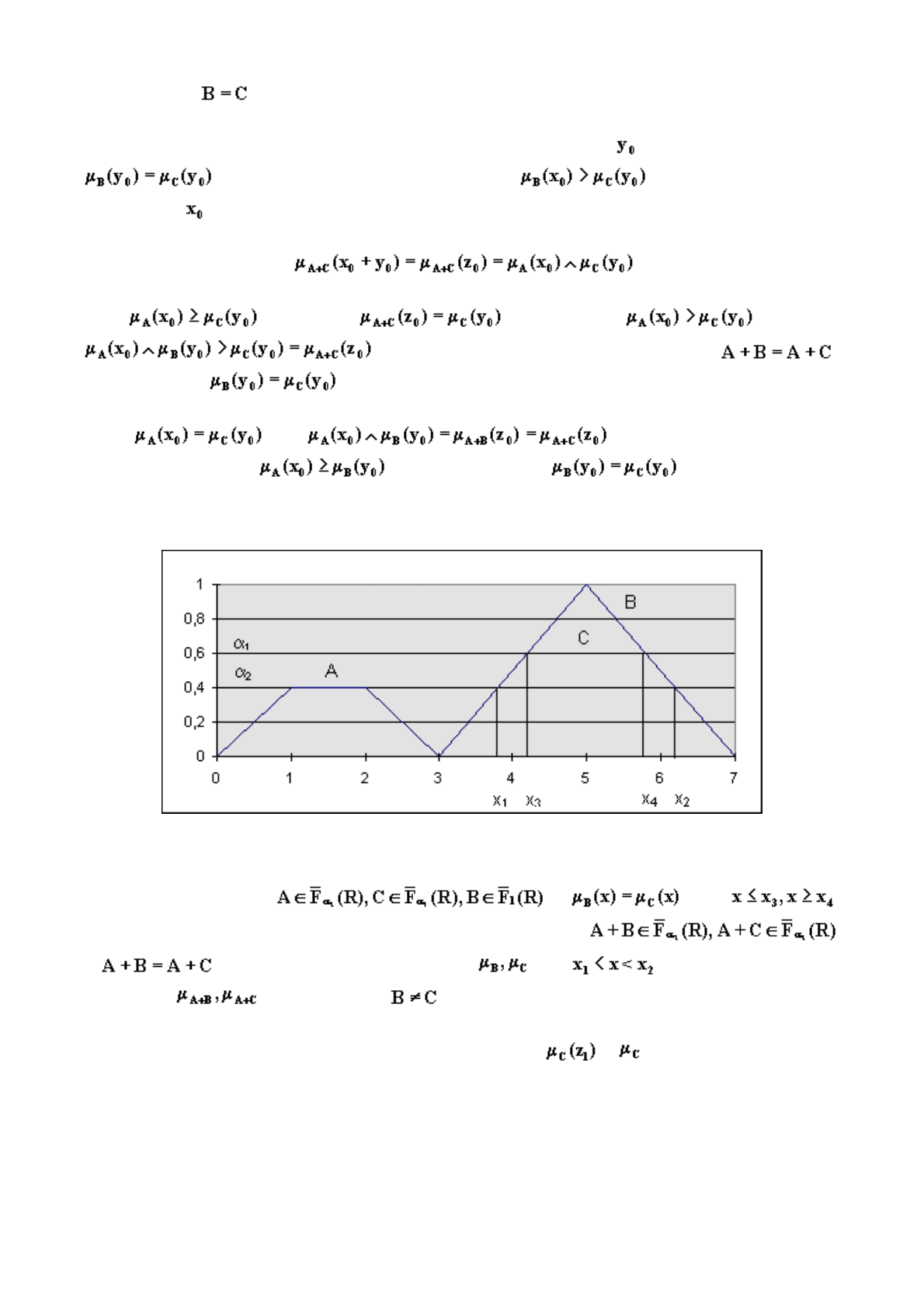
В этом случае .

оказательство

. Покажем, что для произвольного справедливо равенство

. Действительно, пусть, например, . Из условия теоремы

существует такое, что

и , т.е. . Пусть . Тогд

, что противоречит равенству ,

следовательно, .

Если , то , и, следовательно, должно

выполняться условие . Это возможно при . Теорема доказана.

Пример 2.7.

Графически

-величины

изображены на рис.2.4.

Рис. 2.4. Функции принадлежности для примера 2.7.

Из рисунка видно, что и , при .

Из определения операции сложения F-величин очевидно, что

и , поскольку поведение функций при не влияет на значение

F-функций . Тем не менее, .

име

2.8.

На

ис. 2.5 изоб

ажены г

ики

фу

нкций и .

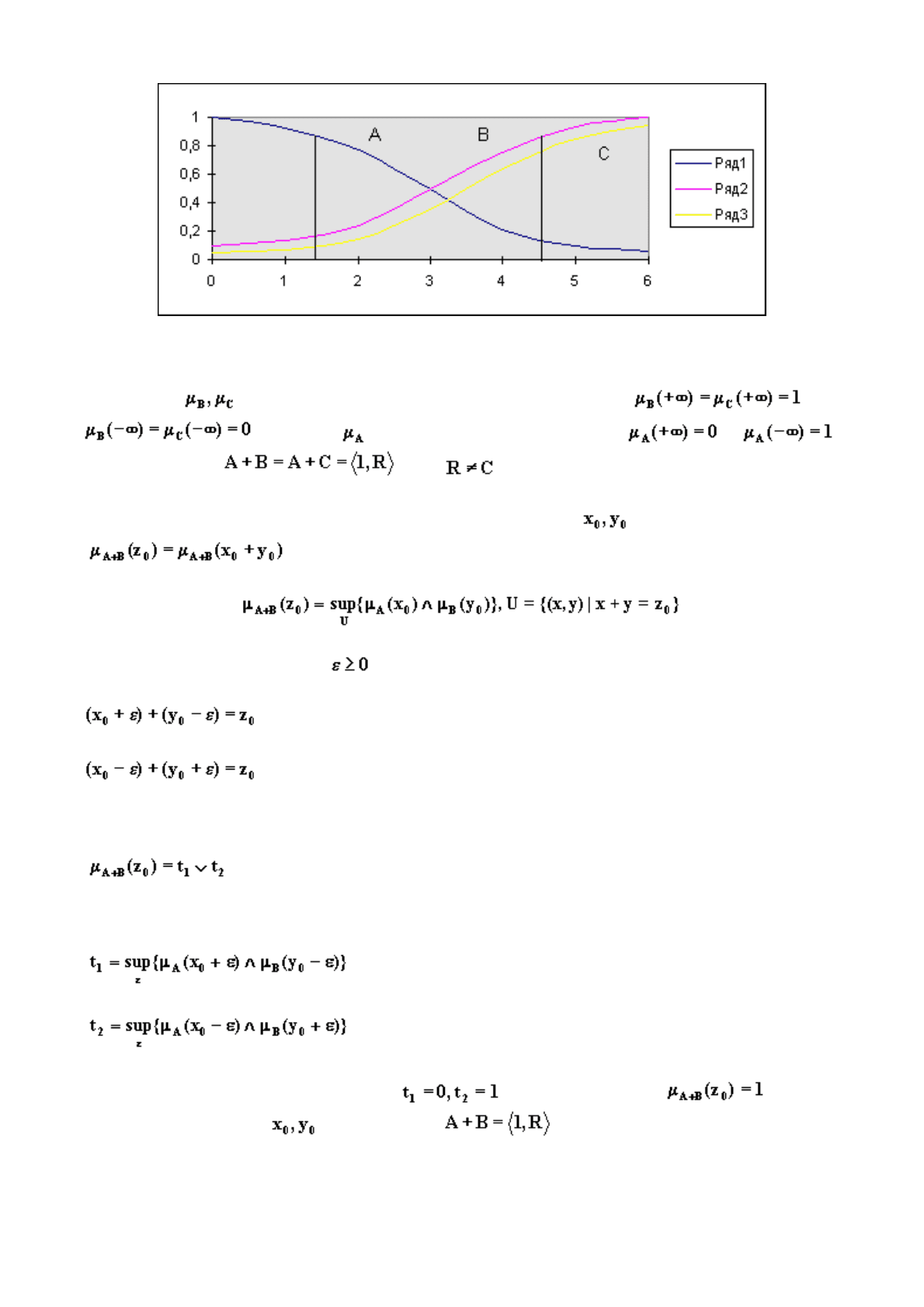
Рис. 2.5. Функции принадлежности для примера 2.8.

Функции монотонно возрастают на всей оси, и

. Функция монотонно убывает на всей оси и .

В данном случае , хотя .

Действительно, возьмем произвольную пару точек и найдем величину

. По определению имеем

Поскольку для произвольного выполняются соотношения

, (2.20)

, (2.21)

то можно записать

, (2.22)

где

, (2.23)

, (2.24)

Очевидно, что для нашего примера и, следовательно, . В силу

произвольности точек получим, что . Это же утверждение справедливо

для

- величин

Нет

ру

дно заметить, что для данного п

име

а не выполняются пе

вые два

словия тео

емы

2.6, т.е., например, для произвольного не существует такого, что

Пример 2.9.

Пусть F-величины А, В и С определяются следующим образом:

т.е. при всех

, кроме

х=2

, т.к. , а . Воспользовавшись

езультатами последующих разделов, имеем

хотя . В данном случае не выполняются те же условия теоремы 2.6, что и в

предыдущем примере.

Пример 2.10.

Пусть

Тогда имеем

хотя . В данном случае нарушено третье условие теоремы 2.6. Действительно,

, но и , но .

Следовательно, равенство не гарантирует равенства , что и показывает

данный пример.

амечани

. Указанное выше определение абелевой полугруппы взято из интервального

анализа, в котором интервальные величины образуют квазилинейное пространство. Этот факт

является очевидным следствием теоремы 2.6, поскольку интервальные величины являются

частным (предельным) случаем F-величин из вида .

2.4. Прямой аналитический метод нахождения результатов

алгебраических операций

Для нахождения результатов алгебраических операций над

- величинами используются

несколько аналитических и численных методов. Причем, если решение ищется для общего

вида записи задачи (2.5), то метод называют

“прямым”

. Если метод основан на некоторой

переформулировке исходной задачи с использованием

-уровней, то его называют

“обратным”

или методом

-уровневых сечений. Как и прежде, основное внимание будет

уделяться операциям первого типа, которые определяются посредством (2.3).

Умножение F-величин на скаляр.

Если

(

λ)

, то в силу взаимной однозначности

отображения

, из (2.3) получим

(2.25)

Если

, то очевидно, что

(2.26)

т.е. если A - нормальная F-величина, то .

Сложение F-величины со скаляром.

Аналогично предыдущему случаю, если

(

λ)

, и,

следовательно,

z=x+

, то

(2.27)

Этим самым осуществляется сдвиг функции вправо или влево по вещественной оси на

величину

Нетрудно проверить, что соотношения (2.25)-(2.27) справедливы и для алгебраических

операций второго типа.

Пример 2.11.

Пусть

(

1-(x-1)

, (0,1)

)

. Тогда, согласно (2.25) и (2.26) имеем

Из (2.27) получим

В разделе 2.2 было отмечено, что нахождение

-величины , т.е. нахождение ее

функции, сводится к решению параметрической экстремальной задачи (2.5). Причем, с

помощью замены из

ур

авнения связи данная задача п

еоб

аз

ется в задач

без

ограничений (2.7), т.е. для операций первого типа получим

. (2.28)

Из теории экстремальных задач [41, 71, 163, 233] хорошо известно, что нахождение

глобального максимума некоторой функции на заданном множестве

из

существенно

упрощается, если эта функция унимодальна, т.е. имеет на

единственный максимум.

Нетрудно заметить, что если

-величина

строго выпукла и функция достигает

на

своей верхней грани, то унимодальна на . Если

- выпуклая, то это уже не так. Тем

не менее, даже для выпуклой

-величины нахождение верхней грани ее

-функции

значительно проще, чем для

-величины с произвольной

-функцией.

Следовательно, предпочтительнее решать задачу (2.28) для выпуклых

-величин, поскольку

функция определяет

выпуклую

-величину. Исключение составляет

операция умножения, когда множества и содержат нуль в качестве внутренней

точки. Кроме того, для выпуклых

-величин справедливо следующее утверждение.

Теорема 2.7.

Если

- выпуклые, то - выпуклая

-величина.

оказательство

. Рассмотрим операцию сложения. Пусть , ,

и , . Тогда для произвольного

имеем

что и требовалось доказать.

Поскольку , а

(-В)

- выпуклая

-величина, то для операции вычитания

утверждение теоремы можно считать тоже доказанным.

Рассмотрим операцию умножения, т.е. . Пусть , ,

и , . Положим для определенности, что

, , . Тогда для произвольного найдутся и

с условием . Пусть , для которых

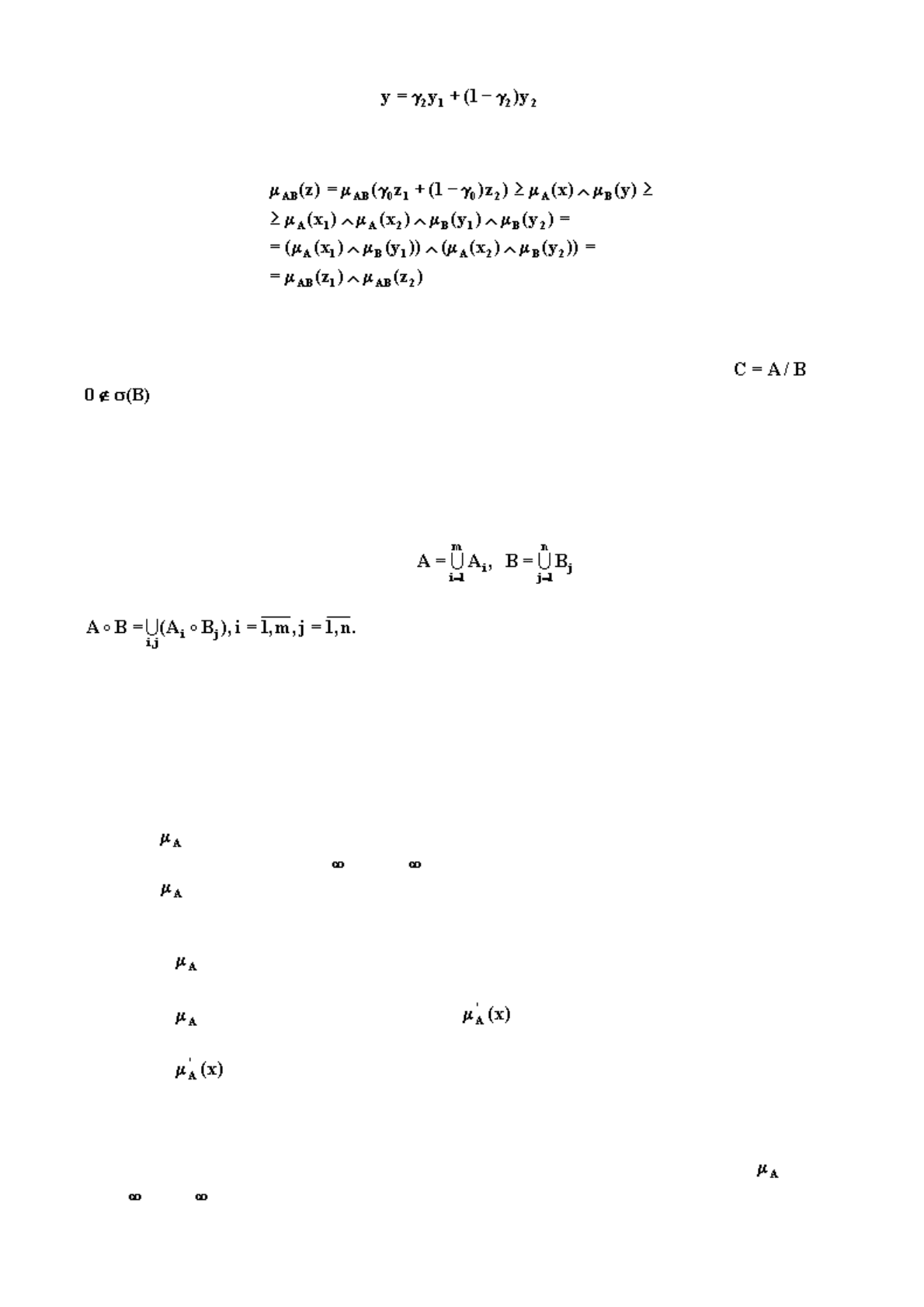
Тогда получим

что и требовалось доказать.

Для операции деления утверждение доказывается аналогично, причем, если , то

. Таким образом теорема доказана полностью.

Предположение о выпуклости

-величин обусловлено также тем, что большинство функций

принадлежности на практике являются выпуклыми. В некоторых случаях может оказаться

полезным следующий подход к решению задачи (2.5), который можно назвать

принципом

декомпозиции

. Если возникает ситуация, когда

- невыпуклые, то их можно представить

в виде объединения выпуклых

-величин. Из определения алгебраических операций над

величинами нетрудно заметить, что если , то

(2.29)

Следовательно, если

- невыпуклые, то представление их в виде объединения выпуклых

-величин в некоторых случаях может облегчить решение задачи (2.5). Имея ввиду все

отмеченные выше обстоятельства, в дальнейшем будем предполагать, что все используемые

F-

величины являются выпуклыми.

В основе прямого аналитического метода для бинарных операций лежит классический подход

к поиску точек экстремума функции на некотором множестве из

. Будем предполагать, что

функция всегда достигает своей верхней грани на

(A)

кроме тех случаев, когда верхняя

грань достигается в точках - или + . Тогда, как известно [41], точками экстремума

функции

(x)

на

(A)

могут быть лишь те точки, в которых выполняется одно из следующих

условий:

1. либо

(x)

терпит разрыв;

2. либо

(x)

непрерывна, но производная не существует;

3. либо существует и равна нулю;

4. либо

x=a

или

x=b

, если

(A)=[a, b]

Если множество

(A)

неограниченно, то нужно также изучить поведение функции

(x)

при

→

- или +.

Рассмотрим теперь каждую из операций над

-величинами.

Сложение F-величин.

В этом случае уравнение связи имеет вид

x+y=z

т.е. для произвольного фиксированного

величина равна верхней грани функции

для (2.3) на прямой в

с уравнением

y= z

-x

. Соотношение (2.28)

запишется в виде

(2.30)

Из (2.30) видно, что значениями функции являются верхние грани семейства F-величин

, зависящих от z как от параметра. Если в зависимости от

экстремальные точки

функции можно выразить в виде соотношений:

(z), x=

(z), ..., x=

n(z)

то получим

где

Следует отметить то обстоятельство, что точка глобального максимума функции

в некоторых случаях может быть получена непосредственно из решения

уравнения

Проиллюстрируем выше изложенное рядом простых примеров.

Пример 2.12.

Пусть , . Тогда из

уравнения имеем , откуда

, и, следовательно, ,

Делая соответствующие подстановки, после несложных преобразований получим

(

2.31

)

Поскольку , то , т.е. .

Пример 2.13.

Пусть и . Тогда из

уравнения

получаем

Делая подстановку , находим

Таким образом,

Пример 2.14.

Если и

, то по аналогии с предыдущим примером из анализа

уравнения

получим, что

(2.32)

Пример 2.15.

Пусть и , где