Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях
Подождите немного. Документ загружается.


методами теории нечетких множеств без привлечения аппарата теории вероятностей.
Получение во всех этих моделях решений в нечеткой форме позволяет довести до сведения
специалиста, принимающего решение, что если он согласен или вынужден довольствоваться
нечеткой формулировкой проблемы и нечеткими сведениями о модели, то он должен быть
удовлетворен и нечетким решением задачи.
1.4. Операции над F-множествами
Все приводимые операции над F-множествами определяются через действия над их F-
функциями.
Множества
А
и
В
из
F(X)
равны
(
А=В
) тогда и только тогда, когда для всех
x
X
.
Для
А
,
В F(X)
множество
А
является
подмножеством
В
(
A B
) тогда и только тогда,
когда для всех
x X
.
Например, если , то
AB
Рис.1.4. Функция принадлежности для нечеткого подмножества
А
Замечание
.
Если
A
и
B
четкие множества и , то , что для
F
-множеств не
обязательно.
Например, если , то ,
но .
Объединением
множеств
А
и
В
из
F(X)
называется множество ,
F
-функция которого
определяется следующим образом:
(1.5)
Объединение соответствует союзу
или
и более компактно записывается как
,

где символ обозначает операцию взятия
max
.
Следствие 1.1.
Множество
С
является
наименьшим
из множеств, содержащих одновременно
А
и
В
.
Д
оказательство
. Пусть
F
-множество и содержит
A
и
В
, т.е.
и т.е. .
Следовательно,
D=C
.
Пример 1.2.
Если , то
, т.е. .
П
ересечением
множеств
А
и
В
из
F(X)
называется множество ,
F
-функция которого
определяется следующим образом:
(1.6)
Пересечение соответствует союзу
и
, более компактно записывается как
,
где символ обозначает операцию взятия
min
.
Пример 1.3.
Если , то
, т.е. .
Следствие 1.2.
Множество
С
является
наибольшим
из множеств, содержащихся
одновременно в
А
и в
В
.
Д
оказательство
. Пусть
F
-множество и принадлежит
A
и
В
. Тогда
и одновременно т.е. .
Следовательно,
D=C
.
Известно, что операции объединения и пересечения четких множеств являются
коммутативными, ассоциативными и обладают свойствами дистрибутивности по отношению
друг к другу. Выявление аналогичных свойств для
F
-множеств сводится к анализу функций

где
Графически эти функции на плоскости при некотором фиксированном изображены
на рис.1.5, где сплошной линией показан график функции
g
, а пунктиром -
f
.
Таким образом,
f
и
g
являются кусочно-линейными и монотонно возрастающими функциями
по каждому из своих аргументов.
Рис. 1.5. Графики функций
Следующие соотношения, которые приводятся без доказательств,
я
вляются следствием
довольно очевидных свойств функций
f
и
g
.
Здесь
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.

Заметим, что если
А
и
В
четкие множества с характеристическими функциями ,
то можно представить в виде (1.2), что эквивалентно определению через
функции
min
и
max
.
Для
F
- множеств это уже не верно, так как
В этом случае следствия 1.1 и 1.2 не выполняются.
Существует несколько способов определения операций объединения и пересечения.
Например, для операции пересечения используют иногда алгебраическое произведение
функций принадлежности
.
Правомерность определения операций объединения и пересечения
F
-множеств в форме
отличной от (1.3) рассматривается в ряде работ [53, 54, 68] с точки зрения принятия решений.
В [60] отмечается, что в некоторых случаях можно задавать в виде среднего
геометрического и, следовательно,
Добавим, что можно описывать с помощью
F
-функции
и , соответственно, в виде
.
Все отмеченные альтернативные варианты объединения и пересечения
F
-множеств только с
определенной степенью точности соответствуют описанию посредством функций min и max.
Поэтому выбор того или иного подхода зависит от конкретной задачи, когда использование
операций min и max приводит к неадекватности модели реальной ситуации.
В принятых обозначениях следующие функции определяют четыре типа операций
пересечения и объединения
F
-множеств:
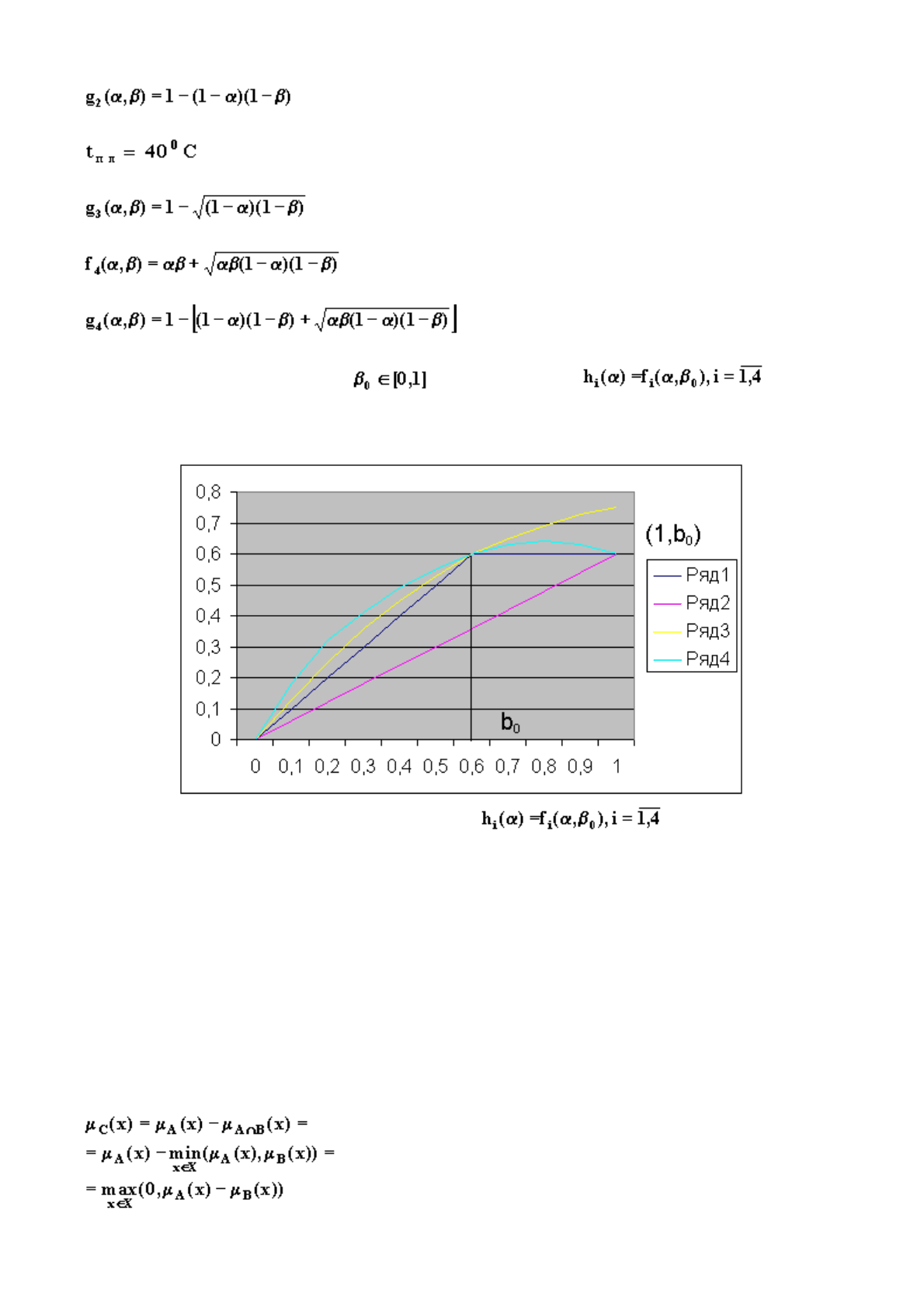
При некотором фиксированном графики функций показаны
на рис. 1.6. Они могут дать некоторое наглядное представление о свойствах отмеченных
типов операций пересечения
F
-множеств.
Рис. 1.6. Графики функций
Аксиоматический подход к определению операций объединения и пересечения
F
-множеств
посредством (1.5) и (1.6) рассматривается в работах [255, 274]. Очевидно, что если
объединить определение объединения со следствием
1.1, а определение пересечения со
следствием 1.2, то получим функции (1.5) и (1.6). Именно так и поступают Беллман и Заде в
р
аботе [54], предполагая минимальность объединения и максимальность пересечения
F
-
множеств в смысле следствий 1.1 и 1.2.
В соответствии с принятой выше индексацией функций
f
и
g
основное внимание в
дальнейшем будем уделять операциям первого типа над
F
-множествами.
Р
азностью
множеств
А
и
В
из
F(X)
называется множество
C=A\B
, с
F
-функцией вида:
(
1.7
)

Разность
X\A
называется
дополнением
F
-множества
A
и обозначается
A
'. Из (1.7) следует,
что
, т.к. .
Эта операция удобна, например, для перехода от нечеткого множества допустимых значений
к множеству недопустимых значений.
Замечание.
Если для четких множеств
А
и
В
из
X
всегда
то для
F
-множеств, вообще говоря, это не верно.
Нетрудно
проверить, что для
А
и
В
из
F(X)
, справедливы следующие соотношения:
1.
2.
3.
4.
5.
6.
7.
8.
Равенства 6 и 7 называются законами де Моргана и следуют, соответственно из тождеств:
1.5. Нечеткие отношения. Проекции
Для практических задач большое значение имеет понятия нечеткого
F
-отношения.
Пусть
X
1
,
X
2
, ...,
X
n
- некоторые множества. Тогда нечеткое
n-арное отношение
Q
определяется как нечеткое подмножество их декартового произведения
X= X
1
*X
2
∗...∗
X
n
, т.е.
Нап
р
име
р
,
фу
нкция
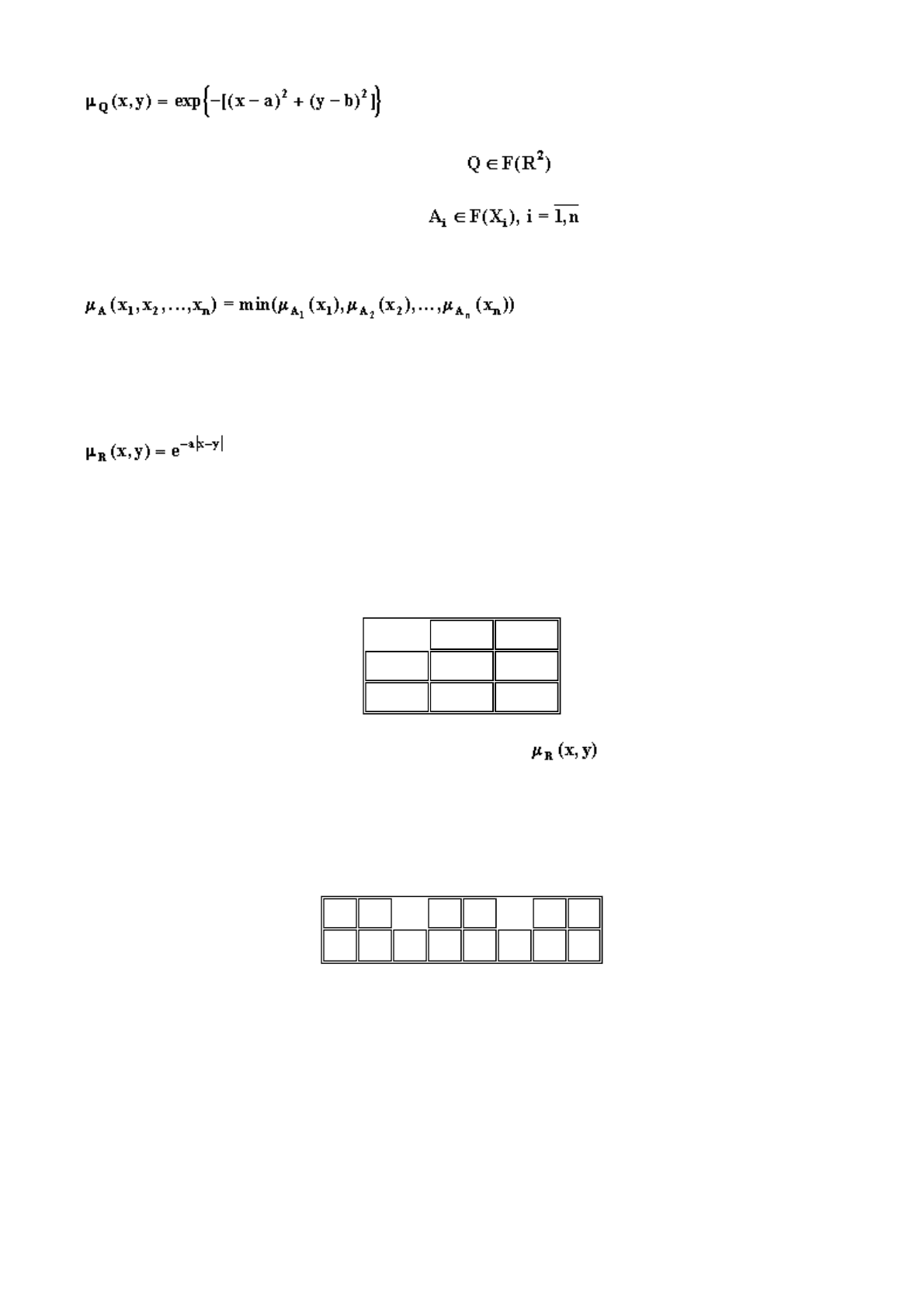
определяет бинарное
F
-отношение
Q
в
R
2
, т.е. .
Д
екартовым произведением
F
-множеств , называется
F
-множество
A= A
1
*A
2
*...
∗
A
n
из
F(X) = F(X
1
*
X
2
*...
∗
X
n
) c функцией принадлежности вида
. (1.8)
Распространенными примерами (бинарных) нечетких отношений являются
много больше чем,
имеет сходство, имеет отношение
и т.д. Например, функция принадлежности отношения
близко к
можно определить следующим образом:
Пример 1.4
. Предположим для примера, что
Х={брат, сестра}
,
Y={отец, мать}
, тогда
бинарное нечеткое отношение
сходства
можно записать в виде:
сходство
= 0,8/(б, о) + 0,6/(б, м) + 0,4/(с, о) + 0,9/(с, м).
Данное отношение можно представить также и в виде матрицы отношения:
в которой
(i,j)
-й элемент равен значению функции для
i
-го значения
х
и
j
-го
значения
у
.
Если множества значений переменных конечны, то матрица
композиции
(
произведения
)
отношений
R
°
S
равна
максиминному произведению
матриц отношений
R
и
S
. В
максиминном произведении матриц вместо операции сложения и умножения используются
операции
Υ
и
Υ
соответственно. Например,
Например, предположим, что
А
и
F
имеют вид:
А
= 0,2/1 + 1/2 +0,3/3
F
= 0,8(1,1) + 0,9(1,2) + 0,2(1,3) + 0,6(2,1) + 1(2,2) + 0,4(2,3)+ 0,5(3,1) + 0,8(3,2) + 1(3,3).
Выражая
А
и
F
с помощью матриц и образуя матричное произведение, получаем
отец
мать
брат
0,8 0,6
сестра
0,4 0,9
0,3 0,8 0,5 0,9 0,4 0,8
0,6 0,9
°
0,4 1 = 0,5 0,9
Важную роль в ТНМ играет понятие
проекции
F
-отношения. Дадим определение проекции
бинарного
F
-отношения.
Пусть - функция принадлежности
F
-отношения в
X
∗
Y
.
Проекции
Q
X
и
Q
Y
отношения
Q
на
X
и
Y
- есть множества в
X
и
Y
с функцией принадлежности вида:
, (1.9)
. (1.10)
Пример 1.5.
Пусть
X=Y=R
- числовая прямая и в
R
2
= X
∗
Y
задано
F
-отношение:
.
Найдем проекции
Q
X
и
Q
y
. Так как - дифференцируема по
x
и по
y
во всей
плоскости, то для любого фиксированного
x
из уравнения
находим, что доставляет максимум функции и, следовательно,
.
Из соображения симметрии .
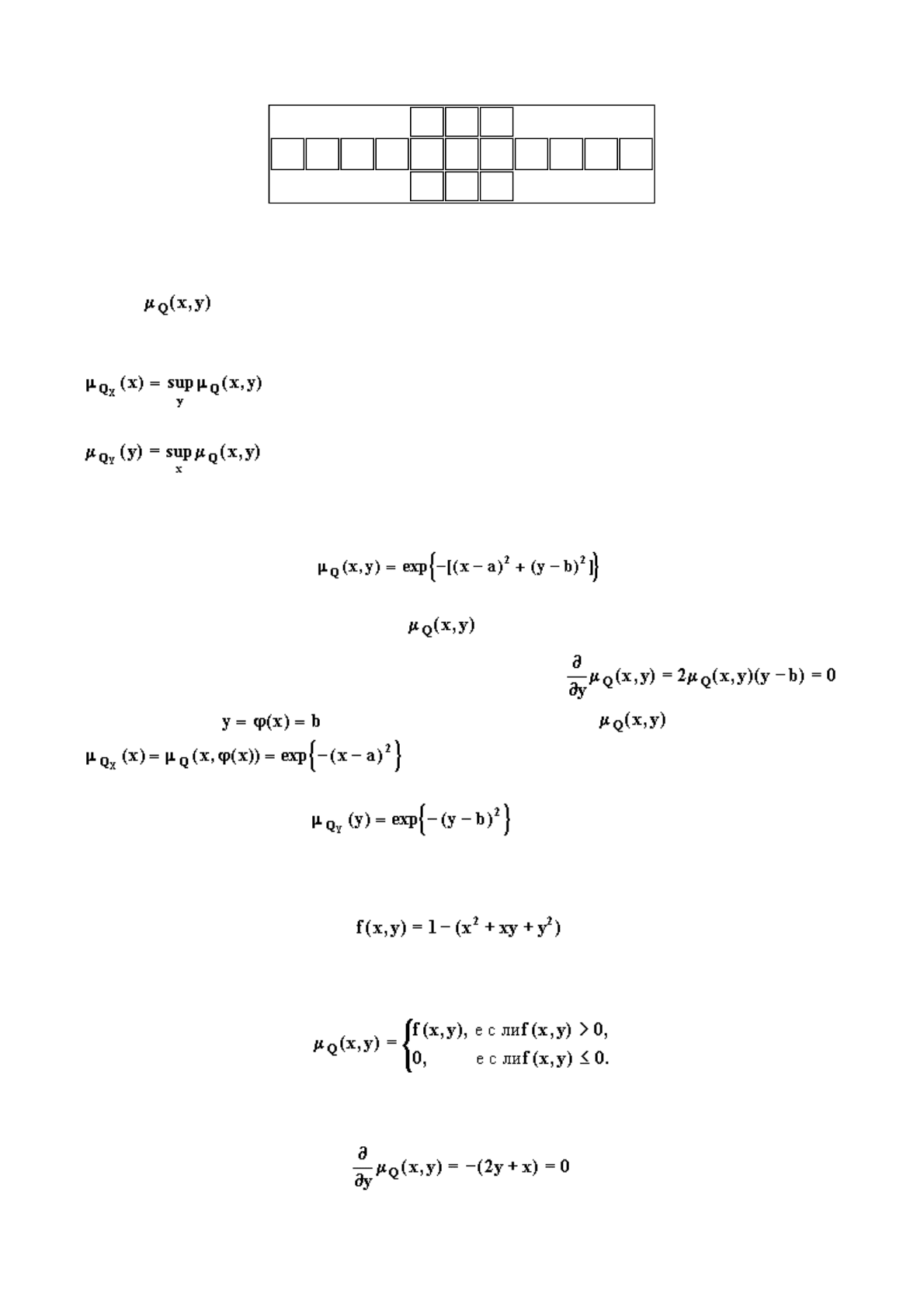
Пример 1.6.
Пусть на
R
2
задана функция:
.
Определим
F
-отношение
Q
в
R
2
следующим образом:
Из уравнения
0,8 0,9 0,2
0,2 1 0,3
°
0,6 1 0,4 = 0,6 1 0,4
0,5 0,8 1

имеем
и, следовательно,
,
Из соображения симметрии .
Условной проекцией
F
-отношения
Q
на
X
при произвольном фиксированном
называется множество с функцией принадлежности вида
. (1.11)
Аналогично определяется условная проекция на
Y
при заданном :
. (1.12)
Из данного определения видно, что проекции
Q
X
и
Q
y
не влияют на условные проекции
P
X
и
P
y
. соответственно. Дадим далее определение, которое учитывает их взаимосвязь.
Условные проекции второго типа
определяются следующим образом:
(1.13)
(1.14)
Если или , то полагаем, соответственно, что или
.
Замечание
. Поскольку для всех х и y выполняется
, , то в выражениях (1.13) и (1.14) ,
.
Кроме того, условные проекции первого типа содержатся в соответствующих проекциях
вто
р
ого типа.

1.6. Независимость проекций
Пусть
X
и
Y
- базовые множества,
Q
- нечеткое отношение в
X
∗
Y
и
Q
X
и
Q
y
- его проекции на
X
и
Y
соответственно.
F
-множества
Q
X
и
Q
y
называются
независимыми
, если
Q= Q
X
∗
Q
y
.
Следовательно, они независимы по первому типу, если
, (1.15)
и независимы по второму типу, если
(1.16)
В противном случае проекции
Q
X
и
Q
y
являются зависимыми (соответствующего типа).
Независимости второго типа можно дать следующую интерпретацию. Соотношения (1.13) и
(1.14) с учетом произвольности
х
0
и
у
0
перепишем в виде
, (1.17)
. (1.18)
Сравнивая (1.17) и (1.18) с (1.16) получаем, что для независимости второго типа необходимо и
достаточно выполнение условий:
, ,
где и - F-функции условных проекций второго типа.
Пример 1.7.
Пусть
X=Y=R
и F-отношение в
R
2
определяется функцией:
.
В этом случае
Следовательно, проекции
Q
X
и
Q
y
независимы как по первому так и по второму типу.
F
-
функции условных проекций первого типа равны
, ,
