Allman E.S., Rhodes J.A. Mathematical Models in Biology: An Introduction

Подождите немного. Документ загружается.

286 Infectious Disease Modeling

individual in the removed class throughout the duration of the model,

but otherwise still uses the basic SI R equations.

a. Explain why this model assumes all vaccinations occur before the

time t = 0.

b. Suppose with N = 100, we have I

= 1, with the removed class

composed of the fraction q of the population that was successfully

vaccinated. Give formulas for S

and R

. What value of q gives the

usual SIR model?

c. Use the MATLAB program sir to investigate the behavior of your

vaccination model for a variety of values of q. Let, for example,

N = 100, α = .001, and γ = .05, and only vary q from0to1.

Explain the qualitative behavior you see. Can you ﬁnd a value of q

that prevents an epidemic from occurring, regardless of the value of

? Estimate the smallest such q.

7.2. Threshold Values and Critical Parameters

To analyze the SIR model and gain some biological insight into the param-

eters in the model, we’ll rewrite the deﬁning equations:

S =−αS

I = α S

− γ I

R = γ I

We will say an epidemic occurs if I > 0 for some time t (i.e., if at some

time the number of infectives grows). If I ≤ 0 for all times, then the size

of the infective class does not increase and no wider outbreak of illness takes

place. The ﬁrst step in understanding disease dynamics, then, is to understand

the sign of I. Thus, we focus our attention on determining whether

I = αS

− γ I

= (αS

− γ )I

is positive, zero, or negative.

First notice from this formula that if I

= 0, then I = 0. This is no

surprise, since if the population is disease free (i.e., has no infectives), it will

remain that way. Having dispensed with this easy-to-understand case, we

can now assume that I

> 0. This means that I will be positive, zero, or

negative according to whether αS

− γ is. Because α>0, we can rephrase

7.2. Threshold Values and Critical Parameters 287

this as:

If S

, then I > 0.

If S

, then I = 0. (7.1)

If S

, then I < 0.

Notice that, from our original formulas, we have S ≤ 0 always, so we

know that S

cannot increase. This means that, if S

, then S

for all

t. Thus, if S

is below the value

, then I < 0 for all times, and the disease

decreases in the population. However, when S

, the number of infectives

will grow and an epidemic occurs.

For this reason, the ratio

is an example of a threshold value; the re-

lationship of S

is an important determinant of the dynamics of the

disease. Because

represents the removal rate γ relative to the transmission

coefﬁcient α, we call it the relative removal rate and denote it by

ρ =

Comparing the initial number of susceptibles S

to the threshold value ρ,we

can determine if an epidemic will occur.



A larger value of γ results in a larger value of the threshold ρ. Does this

make sense? Explain, in terms of the meaning of γ . What affect does a

larger value of α have on ρ? Explain.

A slightly different approach to the same threshold behavior involves re-

writing the equation for I as:

I = γ



− 1



A similar sign analysis of I , using the above expression, shows the impor-

tant question is how the quantity

compares with 1. Mathematical epide-

miologists call the expression

the basic reproduction number of the infection. Sometime you may see this

called the basic reproductive rate or basic reproductive ratio, though, so you

need to be careful about terminology when reading epidemiological studies.

We’ll use the term “basic reproduction number” exclusively. Most impor-

tantly, if R

> 1, then I > 0 and an epidemic occurs.

288 Infectious Disease Modeling

Let’s consider the basic reproductive number R

= (αS

)(

) from

a more biological viewpoint, in order to understand both its name and its con-

ceptual importance. In the SIR model, the term αS

measures the number

of individuals that become infected at the outset of an epidemic. If we divide

by I

, we obtain a “per-infective” measurement: αS

is the number of indi-

viduals who become infected by contact with a single ill individual during

the initial time step.

Actually, if we introduce one infective into an otherwise wholly susceptible

population S

, this ill individual may eventually infect many more than αS

others, since an infective may remain contagious for many time steps. For

example, suppose a young child remains contagious with chickenpox for

about 7 days. Then, using a time step of 1 day, this child would infect about

(αS

)(7) susceptibles over the course of a week.

Moreover, if the period of contagion lasts 7 days, then each day we expect

roughly

or approximately 14% of the total number of infectives to move

from the infective class I

into the removed class R

. Because the removal

rate γ measures the fraction of the infective class “cured” during a single

time step, we have found a good estimate for γ ; we take γ =

≈ .1429. At

the same time, we have found a good interpretation for

: it is the average

duration of the infectious period. In fact, we can estimate γ for real diseases

by observing infected individuals and determining the mean infectious period

ﬁrst.

We have made progress in understanding R

by thinking about this exam-

ple, but we need to summarize a bit:

(

αS

)







no. of new cases arising from one

infective per unit time



average duration

of infection



Thus, R

is interpreted as the average number of secondary infections that

would be produced by one infective in a wholly susceptible population of size

Note that, from this point of view, the threshold value of R

= 1 makes

good biological sense. If R

> 1, then a primary case of disease spawns more

than one secondary case of the illness, the size of the infective class increases,

and an epidemic results. If R

= 1, then a diseased individual produces only

one new case of the disease, and no epidemic can occur; there can be no growth

in the number of infectives. When R

< 1, the disease dies out. In short, an

epidemic occurs if and only if the basic reproduction number R

> 1.

Because the basic reproduction number has such a meaningful interpre-

tation, epidemiologists try to ﬁnd an expression for R

for any model they

7.2. Threshold Values and Critical Parameters 289

propose. Although a complicated model, such as one for a sexually transmit-

ted disease, might include many additional parameters, some combination of

them should be interpretable similarly to R

here. The basic reproduction

number plays a role in public health decisions, because a disease preven-

tion program will be effective in preventing outbreaks only when it ensures

≤ 1.

The severity and duration of epidemics. Once we know a model predicts

that an epidemic will occur, we also want to be able to predict its severity.

Suppose, for a certain disease, one infective is introduced into a population of

500 susceptible individuals. We’ll assume the SIRmodel, and that using time

steps of 1 day is adequate for describing this disease. Suppose, additionally,

that data indicate that the likelihood a healthy individual becomes infected

from a contact with an infective is .1% and that, once taken ill, an infective

is contagious for 10 days.



Justify the calculation of α = .001 and γ = .1intheSIR model.

For these parameter values, we ﬁnd that ρ =

.001

= 100. This means

that we expect about

100

of the susceptibles, or

= .01S

= (.01)500 = 5

individuals to become infected with the illness as a result of contact with the

original sick person. Moreover, because R

= 5 > 1, we expect an epidemic

to occur. In fact, with such a large value of R

, we might expect a rather de-

vastating epidemic to occur.



Notice that I

= αS

+ (1 − γ )I

= .001(500)(1) + .9(1) = 1.4.

Why were there not ﬁve new cases of the disease?



What would the basic reproduction number be if S

= 50? Would an

epidemic occur? Explain.

Using a computer, we can trace the course of the epidemic over a series of

60 days as in Figure 7.1.



Which of the curves represents S

? I

? R

? How can you tell by focusing

on the values at t = 0 and t = 60?

According to the graph, the number of infectives peaks at I

≈ 250 at about

t ≈ 21 or 22 days. As half the population is ill at this time, this is a severe

epidemic, as anticipated.

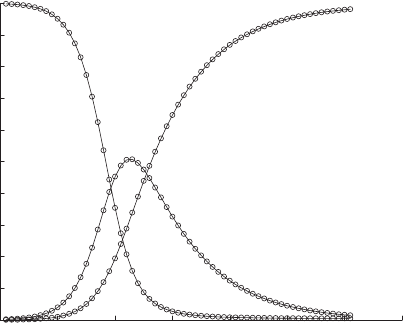
290 Infectious Disease Modeling

0 10203040506070

100

150

200

250

300

350

400

450

500

Figure 7.1. SIR model simulation.

Mathematically, we can determine information about an epidemic’s peak

by noting that the maximum number of infectives occurs exactly when the

sign of I changes from positive to negative. That is, the infective class

will be largest when the number of infectives stops increasing and begins

to decline. Because we have already analyzed the sign of I in Eq. (7.1),

we again see the importance of the relative removal rate as a critical value.

When S

>ρ, the infective class grows. Once S

<ρ, the epidemic will sub-

side. Returning to our example, we calculated that ρ = 100. Consequently,

the epidemic begins to subside when S

= 100, or by the time four-ﬁfths of

the population has contracted the disease. We can verify our calculation by

referring to our graph – indeed, the susceptible population numbers 100 some-

where between the twenty-ﬁrst and twenty-second day after the epidemic be-

gins, and I

peaks just at this time.

Another interesting phenomena can be detected by examining the values

of S

and I

in Table 7.1 that were used to produce Figure 7.1.

Notice that even after the disease has ravaged the population for 100 days,

there are still about two people who have remained disease free. In fact, after

150 days, there are no infectives but two disease-free citizens. Apparently,

two lucky individuals escape the illness, despite the fact that they have no

special immunity to the disease. We can express this long-term behavior, that

as time increases S

approaches a limiting value, by

lim

t→∞

= 2.15.

7.2. Threshold Values and Critical Parameters 291

Table 7.1. S I R Model Simulation

Day 0 1 2 3 ... 20 21 22 23

500 499.50 498.80 497.82 ... 135.59 102.38 76.42 56.99

11.40 1.96 2.74 ... 244.91 253.62 254.23 248.23

Day ... 50 75 100 125 150

... 2.64 2.18 2.15 2.15 2.15

... 20.17 1.54 .12 .01 .00

Perhaps surprisingly, with the SIR model, it is usually the case that

lim

t→∞

= 0. Although the precise value of lim

t→∞

depends on the values of

the parameters α, γ , S

, and I

, it is generally not zero. This means that,

for a disease described well by the SIR model, we should expect some

individuals to never fall prey to the disease, even though they lack any special

immunity.



Does this seem reasonable to you? Can you explain why in intuitive

terms?



Does an epidemic end due to a lack of susceptibles or a lack of infec-

tives? Explain.

Since the SIR model is just a special case of a multiple population model,

it is informative to draw a phase plane plot, just as we did earlier for other

nonlinear models of interaction. Though there are three classes to track, plot-

ting only two of the three classes is sufﬁcient to tell how the third behaves,

because S + I + R = N is constant. We choose to focus on S and I , placing

S on the horizontal axis and I on the vertical one. In Figure 7.2, three orbit

diagrams are shown for the SI R model for various values of the parameters α

and γ . One of the orbits O

corresponds to our example above with α

= .001

and γ

= .1. The parameter values of α

= .002 and γ

= .1 are used for a sec-

ond orbit O

, and α

= .0007 and γ

= .1 for a third orbit O



Which way do the trajectories go along these phase plane plots? Left to

right, or right to left?



Which of the plots is O

? O

? Which epidemic is the most

severe?

The plot in the phase plane gives added insight into the three epidemics

and the SIR model. From the plot of the second orbit O

, the most severe

292 Infectious Disease Modeling

0 50 100 150 200 250 300 350 400 450 500

100

150

200

250

300

350

400

Susceptibles

Infectives

Figure 7.2. SI phase plane for the SIR model.

epidemic, you can tell that the number of infectives increases rapidly at the

onset of the epidemic. In fact, just before the epidemic peaks, I

is increasing

by approximately 80 individuals per time step. In a population of only 500,

this is extreme growth. Of course, a transmission coefﬁcient of α = .002 is

quite large for a population of that size.

Note that you can approximate the relative removal rate ρ from the graphs

of the three orbits, since we know ρ is the value of S

when I

begins to dec-

line. Because S

is also easily read from the graph, once we know ρ, we can

ﬁnd R



Determine from the graph of the orbits approximate values for ρ and

. Do these values match what you would calculate from the values

of the parameters γ and α?

We can make intelligent guesses about the equilibrium points of the SIR

model from the phase plane, too: Each epidemic follows a wave, progressing

toward a point on the horizontal axis. You will see in the problems that the

SIR model has a set of equilibria, including all the points along that axis.

Problems

7.2.1. The SIR model has many equilibria.

a. To ﬁnd the equilibria, why is it not necessary to ﬁnd when R = 0,

if we ﬁnd points where S = 0 and I = 0?

7.2. Threshold Values and Critical Parameters 293

b. Algebraically, ﬁnd the equilibrium points S

∗

, I

∗

for the SIRmodel.

Give a common-sense explanation of why the values you ﬁnd are

equilibria.

c. Are these equilibria stable? Explain intuitively why they should or

should not be.

7.2.2. Suppose the mean infectious period for a certain disease is 37

days.

a. What is the removal rate γ , if time steps of 1 day are used?

b. What is the removal rate γ , if time steps of 1 week are used?

7.2.3. With α = .0008, γ = .1428, and a variety of choices of N , S

, and I

in the SI R model, use a computer program to estimate the value of

at which this epidemic peaks. Now use the formula for the relative

removal rate to determine the value of S

at which the peak of the

epidemic occurs. Do your two answers agree exactly? Explain any

discrepancy.

7.2.4. In Chapter 1, the per-capita growth rate was used to understand the

logistic model. In this problem, we explore the “per-infective” growth

rate.

a. In the SIR model, give a formula for the per-capita growth rate of

the infective class I

b. Plot this relative growth rate as a function of S for the ﬁxed val-

ues of α = .0001 and γ = .2. Place the per-capita rate I /I on

the vertical axis and S on the horizontal axis. Use your graph

to ﬁnd the threshold value S for S

(i.e., ﬁnd the value S such

that an epidemic occurs if S

> S and no epidemic occurs if S

≤ S).

7.2.5. An isolated island population of 100 individuals is exposed to a dis-

ease. The disease is particularly deadly; an infected individual remains

contagious until overcome by death after 4 days. We want to predict

the diseases’s effect on the community on a daily basis. Suppose ini-

tially one individual is stricken with the disease.

a. What is the removal rate γ ?

b. For what values of the relative removal rate ρ will an epidemic

occur? Use this to determine for what values of the transmission

coefﬁcient α an epidemic will occur.

c. Use a computer program such as sir to estimate the number of

days until the epidemic peaks for the values of α = .003, .005, .01,

and .0125, presenting your data in a table. How does the magnitude

of α relate to the time until the peak?

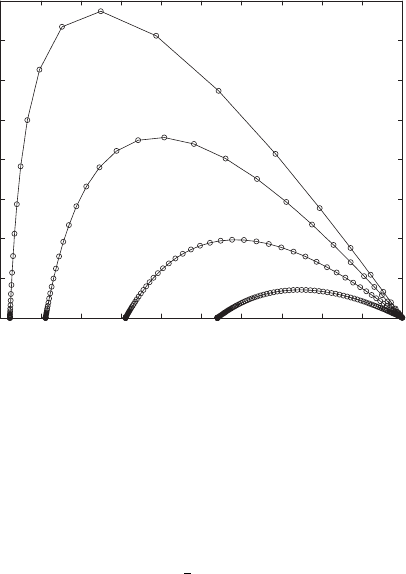
294 Infectious Disease Modeling

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

500

1000

1500

2000

2500

3000

3500

4000

Susceptibles

Infectives

Figure 7.3. SI phase plane for the SIR model.

d. Calculate the basic reproduction numbers and the relative removal

rates for the values of α above, adding that information to your

table.

7.2.6. In a population of 10,000 individuals, a new disease strikes. Once ill,

an infective is contagious for 3

days.

a. Give the removal rate γ , assuming time steps of 1 day.

b. Examine the phase plane in Figure 7.3 for four possible epidemics

with the value of γ determined above. Estimate the relative re-

moval rate ρ and the transmission coefﬁcient α for each of the four

epidemics graphed. Then ﬁnd the basic reproduction numbers for

each of the epidemics. Give your answers in a table.

c. Extend your table in part (b) by including the number of time

steps T until the epidemic peaks, and the number of susceptibles

∞

= lim

t→∞

remaining after the disease dies out. Explain the

effect of increasing α on the virulence of an epidemic. Does this

make biological sense?

7.2.7. A disease strikes a small town of 10,000 individuals. Suppose 10

individuals are infected initially and that the transmission coefﬁcient

has been estimated to be α = .00008.

a. For each of the four possible epidemics plotted in Figure 7.4, esti-

mate the relative removal rate ρ, the removal rate γ , and the mean

time of infectivity. Then calculate the basic reproduction number

for each of the epidemics. Tabulate your answers.

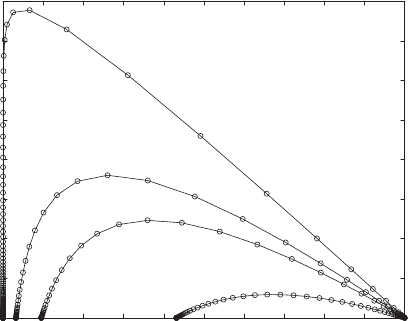
7.2. Threshold Values and Critical Parameters 295

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

1000

2000

3000

4000

5000

6000

7000

8000

Susceptibles

Infectives

Figure 7.4. SI phase plane for the SIR model.

b. Extend your table in part (a) by including the number of tme steps

T until the epidemic peaks, and the number of susceptibles S

∞

lim

t→∞

remaining after the disease dies out. Explain the effect of

increasing γ on the virulence of an epidemic. Does this make

biological sense?

7.2.8. The text claimed that, for the SIR model, there is no epidemic of a

disease if I ≤ 0. For I = 0, you might expect that there is no net

change in the infective class, and so the number of incidences of the

disease should remain constant and the disease would be endemic in

society.

a. Investigate the I = 0 situation experimentally. For instance, set

α = .000035 and γ = .175, and pick values of S

and I

so that

I = 0 initially. Then use a computer program to follow the

growth or decay of the susceptible and infective classes. Record

what you notice. Repeat this for some other choices of the param-

eters for which I = 0.

b. Give a common-sense explanation of why the disease ultimately

dies out when I = 0 initially.

c. Reconsider the difference equations for S and I , and mathe-

matically explain why the disease dies out if I = 0 initially. You

will have to think about two time steps.

7.2.9. In Chapter 3, you learned to draw and interpret nullclines in a phase

plane. Draw a coordinate system with S on the horizontal axis and I

on the vertical axis.