Allman E.S., Rhodes J.A. Mathematical Models in Biology: An Introduction

Подождите немного. Документ загружается.

316 Curve Fitting and Biological Modeling

most important feature of the data, and perhaps eventually lead to a deeper

understanding of the mechanism producing the pattern. Thus, ﬁtting curves to

data is useful in data-driven ﬁelds even when our understanding is too limited

to produce more detailed models.

In this chapter, we will explore some of the basic ideas in curve ﬁtting,

including the most heavily used technique, called least squares. Though the

computations necessary for basic curve ﬁtting are readily performed by most

data analysis software, understanding the mathematical ideas behind them is

helpful in using such software effectively.

8.1. Fitting Curves to Data

As medical researchers develop a new drug, an important issue to be under-

stood is how the concentration of the drug in the bloodstream changes as the

drug is metabolized. To study this, a researcher might administer an initial

dose to bring the concentration to the level of 200 mg/l, and then monitor the

changing concentration over the next few days. Data such as that recorded in

Table 8.1 might be obtained. Notice that no measurement was recorded for

day 2; perhaps the patient missed an appointment or the laboratory work was

botched.

Suppose for therapeutic value, the concentration of drug in the blood needs

to be kept at a level above 100 mg/l. Then, because the table shows the level

dropping below that sometime between 1 and 3 days after the initial dose, the

new dose should be administered sometime in that time period. Unfortunately,

the missing data for day 2 makes it hard to pin down more closely when the

100 mg/l level is crossed.



Based on the available data, do you think the level that would have been

measured on day 2 is greater than or equal to 100 mg/l? How would

you try to persuade someone who disagreed with you?

One approach to answering this question begins with the observation that

the drop in level between times 0 and 1 is much larger than that between times

3 and 4. This might indicate that each passing day produces a smaller drop

Table 8.1. Concentration y of

Drug in the Bloodstream t Days

After Dosage

t (day) 0 1234

y (mg/l) 200 129 — 58 33

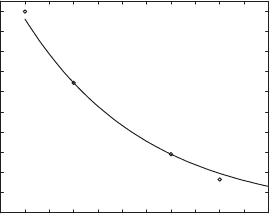
8.1. Fitting Curves to Data 317

100

120

140

160

180

200

t (days)

y (mg/l)

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

Figure 8.1. Data from Table 8.1 with an exponential decay trend.

in level, and so the measurement on day 2 would be lower than the midpoint

between the day 1 and day 3 measurements. Since (129 + 58)/2 = 93.5,

probably the day 2 measurement would have been less than 100 mg/l.

Although this sort of reasoning is ﬁne as far as it goes, it’s inadequate for

answering more reﬁned questions. For instance, what is the best estimate of

the level on day 2? This is a question of interpolating the data to estimate

values between entries in the table. If, instead, we wanted to estimate the level

on day 5, then we need to extrapolate, because we have data entries on only

one side of that day.

Plotting the above data produces the points marked in Figure 8.1. The

data points appear to cluster along an exponential decay curve like the one

shown. Finding a formula for that curve, or a similar one that ﬁts the data

well, would enable us to both describe the data and estimate unknown values

easily. Interpolating and extrapolating could be performed by simply plugging

time values into the formula for the curve. A curve that describes the data

well overall, though perhaps not in all its particulars, serves as a model for the

data. Because exponential decay curves are described by formulas of the form

f (t) = ae

with k < 0, our goal is to ﬁnd the best choice of the parameters

a and k to ensure a good ﬁt between the data and the model.

You might imagine that just collecting more data, by taking more frequent

measurements over a longer time, would be preferable to ﬁtting a curve to the

data we have. Even if we collect more data, though, we would still ﬁnd it useful

to ﬁt a curve to it. Finding a formula that describes the overall trend in the data

would give a succinct description of it, and might give us more insight than the

raw numbers that were collected. Also, we should expect minor ﬂuctuations in

the data around its overall trend, due to measurement errors and the speciﬁcs

318 Curve Fitting and Biological Modeling

of the patient’s activities during the period of the study. Fitting a simple curve

to the data is, like most models, a way of focusing attention on main features

and ignoring details we consider less important.

Our ﬁrst approach to ﬁnding a and k is a simple one. We can use the data

points to get relationships between the parameters by plugging the points into

the equation f (t) = ae

. For instance, the data point (1, 129) gives

129 = ae

With two unknowns in this equation, we cannot yet solve, so considering

another data point, say (3, 58), gives

58 = ae

Now, the ﬁrst equation gives a = 129e

−k

, which can be substituted into the

second to obtain

58 = (129e

−k

= 129e

Thus

129

= e

so taking a natural logarithm, we ﬁnd

k =

129

≈−.3997.

Now, because a = 129e

−k

, using this value of k to solve for a gives a ≈ 192.4.

Thus, our ﬁrst attempt at ﬁtting an exponential curve to the data yields

(t) = 192.4e

−.3997t

This curve is the one that was graphed in Figure 8.1.



What does this curve indicate as the amount of drug in the patient at

time t = 2? At time t = 5?

Looking at the ﬁgure carefully, we notice that the graph of y = f

(t) passes

through exactly two of the data points, but is only near the others. We should

have expected this, because we used only two data points to solve for a and

k. We have completely ignored 2 of the 4 measurements that were taken. This

is, of course, a signiﬁcant drawback to our approach.



Suppose another researcher chooses the ﬁrst two data points and solves

for the constants a and k. How would the resulting curve compare with

the one above? Do you think it would be a better model?

8.1. Fitting Curves to Data 319

If different researchers propose different curves as good ﬁts to the data, an

objective way of measuring the ﬁt is needed. A start at measuring goodness of

ﬁt between a curve y = f

(t) and data is to look at the difference between the

y-coordinates of the data and the y-coordinates of f

(t). We can gather these

differences into an error vector e. For the data and curve y = f

(t) above, we

ﬁnd the error is

≈ (200, 129, 58, 33) − (192.4, 129.0, 58.00, 38.89)

≈ (7.6, 0, 0, −5.89).

Note that a data point below the curve produces a negative error and that one

above produces a positive error. As already observed, at the two points used

in ﬁtting the curve, the individual errors are zero, or at least very close to zero

due to rounding.

A major ﬂaw in our ﬁrst curve-ﬁtting attempt is that it only used some of

the data points in ﬁnding an equation. One possible way around this problem

is to ﬁt the data to a curve with more parameters. For instance, with the data

above, ﬁtting an exponential of the form g(t) = ae

+ b would use three data

points because of the three parameters a, k, and b. The resulting curve g(t)

will pass exactly through those three points, making three entries in the error

vector be equal to zero.

Although the idea of including more parameters in the curve seems attrac-

tive at ﬁrst, it could be a real mistake. For instance, as one of the exercises

will show, there is a theoretical model that justiﬁes why a curve of the form

f (t) = ae

is really the appropriate one for dealing with the metabolization

of a drug. Even in situations where no such theory exists, it is often better to

use simple formulas to ﬁt data rather than complicated ones. After all, some

of the details in the data may be due to experimental artifacts and random

variations, and are not really part of the trend we hope to capture. A simple

curve that comes close to all data points may therefore be a more valuable

description than a complicated curve that exactly hits all points.

Semilog and log–log graphs. As a second attempt to ﬁtting a curve f (t) =

to the data above, we will try to use all the data points. Of the two unknown

parameters, a and k, we might think that k is more important because it

indicates the rate of decay. This suggests that we should focus on a technique

of ﬁnding the decay rate k using all of the data points.

A clever way to estimate k is to use a semilog plot. For the moment,

view our four data points as approximated by ordered pairs of the form

(t, y) = (t, ae

). If we transform the data by taking natural logarithms of the

320 Curve Fitting and Biological Modeling

Table 8.2. Semilog Transformation of

the Data in Table 8.1

t01234

ln y 5.298 4.860 — 4.060 3.497

y-coordinates, we obtain ordered pairs of the form (t, ln y) = (t, kt + ln a).

Notice that the new second coordinates of these points have a simpler pat-

tern; they are now linear functions of t, because they have the form kt + ln a,

where k and ln a are just constants. If we could ﬁnd the slope of the line

relating these transformed data points, then that would be a good estimate for

k, the decay rate.

In a semilog plot, we graph the transformed data (t, ln y). The name refers

to the fact that we take a logarithm of only one of the coordinates. (Although

it is also possible to form a different type of semilog plot using (ln t, y), that

would not help us here, since our goal is to estimate k as best we can.)

The semilog transformation of the data of Table 8.1 gives Table 8.2 and

Figure 8.2. The ﬁgure shows how a semilog transformation converts nearly

exponential data into nearly linear data.

Although Figure 8.2 might lead us to guess that k ≈−.5, it’s best to per-

form a calculation with all the data points to estimate the slope. A reasonable

idea is to ﬁrst ﬁnd the slopes of the line segments joining adjacent transformed

data points and then use the average of those three slopes as an estimate for k.

The slope between the ﬁrst two transformed data points is m ≈ (4.860 −

5.298)/(1 − 0) =−.438. Similarly, we ﬁnd the slopes between the other pairs

of consecutive points as −0.400 and −0.563. Finally, taking the average of

these slopes, we estimate k ≈ (−.438 − .400 − .563)/3 =−.467.

3.5

4.5

5.5

t (days)

ln(y)

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

Figure 8.2. Semilog plot of the data in Table 8.1: (t, ln y).

8.1. Fitting Curves to Data 321

Note that this estimate of the growth rate k is slightly different from that

found in our ﬁrst attempt at curve ﬁtting in which we used only two data

points. Although we still do not know if this estimate of k is better, we might

suspect that it is because we used all the data in the estimation procedure.

To ﬁnish ﬁnding the equation f

(t) = ae

−.467t

that models the data, we

must pick a value for a. A quick way is to use one of the data points to solve

for a. We will choose one of the middle data points, (1, 129), in the hope that

its central location in the data set might make the curve f

(t) ﬁt the data the

best. Substituting t = 1 and y = 129 and solving, we obtain a ≈ 205.8, and

(t) = 205.8e

−.467t



How might you better estimate a in a way that uses all of the data?

The idea of transforming data with a logarithm was useful here because it

converted exponential decay into linear behavior. A similar approach is useful

when we believe a curve given by a power function y = ax

should ﬁt our

data. For this particular curve, taking a logarithm of both x and y is useful,

because

y = ax

is equivalent to ln y = n ln x + ln a.

This means that a graph of the points (ln x, ln y) = (ln x, ln a + n ln x) will

form a line, with slope n. Such a plot is called a log–log plot. If a log–log

plot of data looks close to linear, then a good estimate of the slope of the line

will be a good estimate for the degree of the correct power function to ﬁt.

Indeed, if we can ﬁnd a good estimate for the equation of the line relating

ln x and ln y, say ln y ≈ m ln x + b for some m and b, then exponentiating

this equation gives y ≈ e

, which is a power function ﬁtting the data.

Signiﬁcantly, semilog and log–log transformations allow us to reduce the

problem of ﬁtting either exponential or power functions to data to that of ﬁtting

a line to transformed data. If we develop a means of ﬁnding good models for

linear relationships between variables, then by using various transformations

on our data if necessary, we will also know how to ﬁnd good models of certain

other types of relationships.

Measures of error. So far, we have used two ad hoc methods to ﬁt an

exponential curve to four data points. Both

(t) = 192.4e

−.3997t

and f

(t) = 205.8e

−.467t

are reasonable candidates for exponential curves ﬁtting the data, but which

is better? Although we suspect that the second curve f

(t) = 205.8e

−.467t

probably describes the data better than f

(t) = 192.4e

−.3997t

, since we at

322 Curve Fitting and Biological Modeling

least used all the data in ﬁnding it, we need to be precise about what “better”

means. Using graphical perception or vague suspicions to choose which graph

is superior is too subjective; a different viewer might choose differently.

Earlier, we determined that the vector of errors for f

(t) was given by

≈ (7.6, 0, 0, −5.89).

Each of these numbers measures the vertical displacement between a data

point (t

, y

) and the point (t

, f

)) on the graph of f

(t) with the same t

value. Calculating the error vector e

for f

(t)’s ﬁt to the data gives







200

129







−







205.8e

−.467(0)

205.8e

−.467(1)

205.8e

−.467(3)

205.8e

−.467(4)







≈







−5.8

7.3

1.22







Note that only one of the entries of e

is zero. Also, whereas e

had two zero

entries, it also has an entry larger than any of those in e

. Apparently, there

has been a sort of trade-off, where ﬁtting perfectly at two points produces a

worse ﬁt at others.

Instead of comparing corresponding entries in error vectors one at a time,

the individual errors can be combined into a single scalar that measures the

overall ﬁt. To compute a measure of the total error for each of the ﬁtting

curves, we might try adding the components of the error vector. Unfortunately,

because some of the components of the error vectors are positive and some

are negative, there would be some cancellation. The number computed would

give too small a measure of the total error.

A better idea is to sum the absolute value of the errors. This is called the

total deviation for the ﬁt of the curve to the data. For the error between f

and the data,

TD( f

) =|7.6|+|0|+|0|+|−5.89|=13.49,

whereas for f

TD( f

) =|−5.8|+|0|+|7.3|+|1.22|=14.32.

Total deviation, therefore, gives a quantitative reason to say that f

ﬁts the

data better than f

A second way to overcome the cancellation problem is to square each of

the entries of the error vector. This is called the sum of squares for error.

SSE( f

) = (7.6)

+ 0

+ (−5.89)

= 92.4521

SSE( f

) = (−5.8)

+ (0)

+ (7.3)

+ (1.22)

= 88.4184

8.1. Fitting Curves to Data 323

Note that using SSE to measure total ﬁt indicates that f

was a better ﬁt than

As this example shows, SSE and TDgive genuinely different criteria for

determining which ﬁt is best. Although both are reasonable measures of total

error in ﬁtting a curve to data, one must be chosen so that we have a standard

way of comparing. The SSE measure of ﬁt is the one most heavily used by

scientists, and the one on which we will focus. As some of the exercises will

indicate, TD has some unpleasant properties that make it a poorer choice.

The use of SSE can also be grounded in statistical models of error.

But, even if we decide to use SSE to measure total ﬁt, there might be an

exponential curve that ﬁts the data even better than f

does. We have found

two particular curves, based on two approaches that happened to come to

mind, yet there may be a still better curve that we have not thought of. How

we can ﬁnd the best curve will be a question for the next section.

Problems

8.1.1. Find a formula for the exponential f (t) = ae

that passes through

the ﬁrst two data points in Table 8.1. Then compute the error vector,

measuring its ﬁt to the data. Is it a better or worse ﬁt than the function

(t) found in the text when the total error is measured by TD? Than

(t) when total error is measured by SSE?

8.1.2. In the second approach of this section to ﬁnding an exponential curve

to ﬁt the data in Table 8.1, all data points were used to estimate k,but

only one to estimate a.

a. Invent a scheme that uses all points to estimate a (after k has been

estimated) and carry it out.

b. Use SSE to determine if the curve you found in part (a) is a better

or worse ﬁt than y = f

(t).

8.1.3. Consider the three data points: (2, 7.6), (5, 15.3), (10, 32.1). Three

candidates for best-ﬁt line for this data are

y = 2.9x + 1.9, y = 2.9x + 2, y = 3x + 1.1.

a. Plot the data points and the three lines on the same graph. (In MAT-

LAB this can be done with the commands like: x=[2,5,10],

y=[7.6,15.3,32.1], plot(x,y,'o'), hold on, L1=

3*x+1.1, plot(x,L1).) Which of the three appears to be the

best ﬁt?

324 Curve Fitting and Biological Modeling

b. For each line, compute the error vector and SSE. Which of the three

lines ﬁts the data points best by giving the smallest SSE?

c. By looking at your graphs and making informed guesses, try to

ﬁnd a line that produces a smaller SSE than any of the three given

ones.

8.1.4. Drug levels in the bloodstream are typically observed to decay expo-

nentially with time from the administration of a dose. A difference

equation model that describes this (and gives further reason to try to

ﬁt the data of Table 8.1 to an exponential curve) is y

t+1

= (1 −r )y

where r is the percentage of the drug that is absorbed by tissue or

broken down by metabolization during one time step.

a. If the initial amount of the drug is y

, explain why this model leads

to y

= y

(1 − r )

b. Letting k = ln(1 − r) and a = y

, show this is equivalent to y

c. Explain why 0 < r < 1 for this model, and then why k < 0.

8.1.5. You might think that the four data points in Table 8.1 could be modeled

well with a straight line.

a. Using only the two middle data points, ﬁt a straight line y = mt + b

to the data. Compute the error and SSE. Is your line a better or worse

ﬁt than y = f

(t)?

b. Invent a scheme to ﬁnd a straight line that ﬁts the data better than

the line you found in part (a). Compute its SSE. Is it a better or

worse ﬁt than y = f

(t)?

8.1.6. At times t = 1, 2, 3, 4, 5, and 6 seconds, data values y

= 3, 7, 17,

37, 82, and 182 are recorded.

a. Plot the data. (In MATLAB, after storing the t and y values in

vectors, use plot(t,y,'o').) From this graph, do you think

a linear, exponential, or power function is the best model for the

data?

b. Produce a semilog plot and use it to roughly estimate the growth

rate k for a model of the data given by a curve of the form y = ae

(In MATLAB, plot(t,log(y),'o') will produce the plot.)

c. Produce a log–log plot and use it to roughly estimate the degree n

of a power function, for a model of the data of the form y = at

. (In

MATLAB, plot(log(t), log(y),'o') will produce the

plot.)

8.1.7. Using TDto measure total error can sometimes ignore a piece of data,

as this problem will show.

8.2. The Method of Least Squares 325

Consider the three points (0, 0), (1, C), and (2, 0), where C > 0,

and the problem of ﬁnding the best horizontal line y = b to ﬁt these

points.

a. Explain why any horizontal line below all three points cannot be

the best ﬁt, by drawing a plot and imagining what happens to TD

as the line is moved upward.

b. Explain similarly why any horizontal line above all three points

cannot be the best ﬁt.

c. Explain why, if a horizontal line is below the middle point and

above the others, then TDcan be decreased by lowering the line to

go through the bottom two points.

d. Conclude y = 0 is the best-ﬁt horizontal line when TDis used as

a measure of total error. Because this result does not depend on C,

the value of C has no effect on the line.

e. For a challenge, explain why y = 0 is the best-ﬁt line (horizontal

or not) for the three data points.

8.1.8. Using TD to measure total error does not always produce a single

best-ﬁt curve; there can be many curves that are all equally good.

To see how this can happen, consider the four points (0, 0), (1, 1),

(2, 1), and (3, 0), and the problem of ﬁnding the best horizontal line

y = b to ﬁt these points.

a. As in the previous problem, explain why the best-ﬁt horizontal line

cannot lie above all the points or below all the points.

b. Explain why any horizontal line above the two bottom points and

below the two top points will have TD= 2.

c. Conclude from parts (a) and (b) that there may not be a unique

solution to the problem of ﬁtting a curve to data, if total error is

measured using TD. (If total error is measured by SSE, there is a

unique best-ﬁt line.)

8.2. The Method of Least Squares

While exploring the idea of ﬁtting curves to data in the last section, we

discovered that even ﬁtting an exponential curve to data could be reformulated,

through the use of semilog graphs, as a problem of ﬁtting a straight line.

In fact, the most common curve-ﬁtting problems experimentalists face are

usually those of straight line ﬁts. Data are collected, a plot is made (using

a transformation if necessary), and the data points often appear to cluster in

a roughly linear manner. Then, the best-ﬁt line to describe the data must be

chosen.