Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems
Подождите немного. Документ загружается.


C HALLENGE 10
Corollary 4. If the unstable manifold of p in Proposition 3 enters two other
basins B
2
and B
3
(where bas(Q),B
2
, and B
3
are pairwise disjoint), then every
boundary point of bas(Q) is also in the boundary of B
2
and B
3
, and thus bas(Q)
is a Wada basin.
Remark. In the basin picture for the pendulum in Chapter 2, the three
basins shown are disjoint and each has a basin cell. Figure 10.30 depicts basin
cells for each of the three basins. The orbits that generate each of these cells have
unstable manifolds that enter all three basins. Hence, the boundary of each basin
equals the boundary of all three basins.
439

S TA B LE M ANIFOLDS AND C RISES
E XERCISES
10.1. Prove that the stable manifold and unstable manifold is invariant under a diffeo-
morphism f.
10.2. Let f be a one-to-one linear map of
⺢
2
. Describe the possible stable and unstable
manifolds of 0.
10.3. Figure 10.12 shows part of the stable and unstable manifolds of a saddle p of a planar
diffeomorphism.
(a) Show that if x is a transverse homoclinic point, then f(x)andf
⫺1
(x)are
transverse homoclinic points.
(b) Extend the stable and unstable manifolds shown in the figure to include
three forward and three backward iterates of each homoclinic point shown.
10.4. Let f(x, y) ⫽ (x 2, 2y ⫺ 7x
2
). Verify that 兵(x, 4x
2
):x 僆 ⺢其 is on the stable manifold
of the fixed point (0, 0). Why can you then conclude that 兵(x, 4x
2
):x 僆 ⺢其 is the
stable manifold?
10.5. Let f(x, y) ⫽ (x
2
⫺ 5x ⫹ y, x
2
). What information does the Stable Manifold Theo-
rem give about the fixed points of f? In particular, plot the fixed points and indicate
in the sketch the action of the map in a neighborhood of each fixed point.
10.6. Assume that f is an invertible map of the plane. Use the Stable Manifold Theorem
to show that a stable manifold of a saddle has no endpoints and that it does not
cross itself. (Of course, the same properties hold for an unstable manifold, as well.)
10.7. For the map f(x, y) ⫽ (x ⫹ y(mod1),x⫹ 2y(mod1)), describe the unstable manifold
of (0, 0). Show that the stable and unstable manifolds meet at right angles.
10.8. State a Stable Manifold Theorem in the case that f is a diffeomorphism of
⺢
n
.
10.9. Let f be a horseshoe map defined on the unit square which is linear for (x, y)in
[0, 1] ⫻ ([0, 1 3] 傼 [2 3, 1]). To be specific, define
f(x, y) ⫽
(x 3, 3y)if0ⱕ y ⱕ 1 3
(1 ⫺ x 3, 3 ⫺ 3y)if2 3 ⱕ x ⱕ 1.
For (x, y)in[0, 1] ⫻ (1 3, 2 3), define f in such a way that f is one-to-one and
smooth. (The picture to keep in mind is the standard horseshoe image.) Notice
that (0, 0) is a fixed-point saddle of f. Calculate explicitly the stable manifold and
unstable manifold of (0, 0) (at least the parts that lie within the unit square—there
will be many parts).
440
L AB V ISIT 10
☞ L AB V ISIT 10
The Leaky Faucet: Minor Irritation or Crisis?
O
NE OF THE EARLIEST physical experiments to exhibit interesting dynam-
ical behavior was the leaky faucet. Here is an experiment you can try at home.
Some faucets work better than others; it helps to use a metal sink or in some other
way exaggerate the noise of the falling drip. You should be able to just barely open
the faucet and establish a pattern of drops evenly spaced in time. Now increase
the flow rate slightly. The drops will speed up but remain evenly-spaced in time. If
you can increase the flow rate finely enough, you should eventually reach a stage
where the pattern changes qualitatively: the drops come in pairs, a short followed
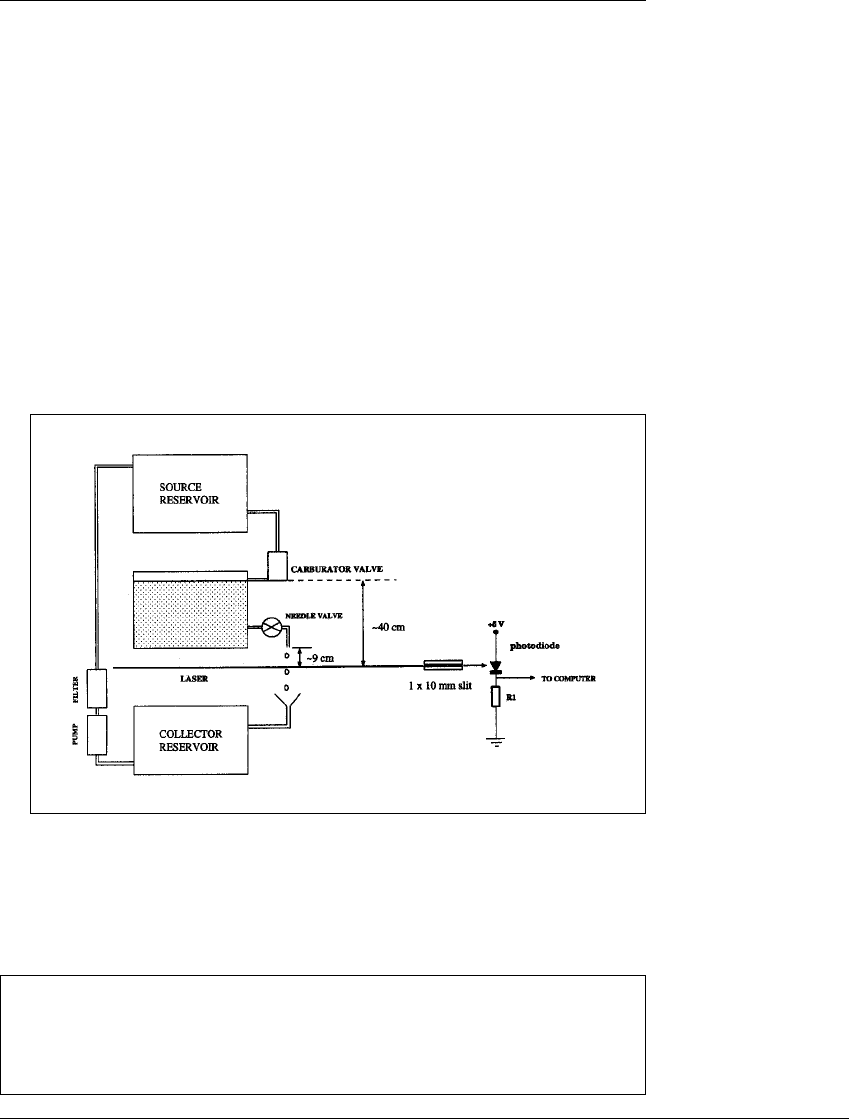
Figure 10.31 Diagram of the leaky faucet apparatus.
A carburetor valve is used to keep the main reservoir filled to a constant level,
which holds the pressure at the needle valve constant. Drops are recorded when
they break the laser beam which falls on the photodiode.
Martien, P., Pope, S. C., Scott, P. L., Shaw, R. S. 1985. The chaotic behavior of the
leaky faucet. Physics Letters A 110: 399–404.
Sartorelli, J. C., Goncalves, W. M., Pinto, R. D. 1994. Crisis and intermittence in a
leaky-faucet experiment. Physical Review E 49: 3963–3975.
441

S TA B LE M ANIFOLDS AND C RISES
by a long. Each short-long pair will take about as much time as two evenly-spaced
drips before the transition. The change you have witnessed is a period-doubling
bifurcation.
With laboratory equipment, a more quantitative study can be made, which
uncovers a great variety of dynamical phenomena. Two groups, one from Santa
Cruz, California, and one from Sao Paulo, Brazil, have done controlled experi-
ments of the leaky faucet. The setups are similar. A reservoir of distilled water is
kept at constant pressure at a needle valve, which can be controlled with great
precision. Drips from the valve are detected by a laser beam trained on the drip
stream and recorded by computer. Figure 10.31 shows the Sao Paulo apparatus;
the Santa Cruz version is similar, although they used a carburetor valve from a
Model A Ford automobile.
The period-doubling bifurcation we described above can be seen graphically
in Figure 10.32, taken from the Santa Cruz experiment. The measured quantity
in the experiments is the time interval T
n
between drips. Each part of the figure
Figure 10.32 Scatter plots of successive interdrip intervals.
Pairs of form (T
n
,T
n⫹1
) are plotted. (a) Period-one. (b) Period-two. (c) Period-four.
(d) Chaos.
442

L AB V ISIT 10
Figure 10.33 A bifurcation diagram for the leaky faucet.
Each vertical slice is 1024 dots corresponding to interdrip intervals. A period-three
window (I3), an interior crisis (I), and a boundary crisis (B) are identified.
shows a scatter plot of ordered pairs (T
n
,T
n⫹1
). A simple rhythmic drip pattern
corresponds to equal interdrip intervals T
n
⫽ T
n⫹1
⫽ T
n⫹2
⫽ ..., so that the
scatter plot of (T
n
,T
n⫹1
) is reduced to a single point. Figure 10.32(a) shows this
simple dynamics. Each interdrip interval is approximately . 094 seconds.
The result of gradually increasing flow rate from the needle valve is the be-
ginning of a period-doubling cascade of bifurcations. Figure 10.32(b) and (c) show
period two and four behavior, respectively. Figure 10.32(d) exhibits a more com-
plicated relationship between successive intervals which presumably corresponds
to chaotic dynamics. This plot cannot exactly be compared to a one-dimensional
map T
n
→ T
n⫹1
, since there appear to be two distinct bands of points (T
n
,T
n⫹1
)
over a range of T
n
values.
Figure 10.33 shows a bifurcation diagram made by the Sao Paulo group. The
bifurcation parameter, the flow rate at the needle valve, was set at 208 different
values to make this plot. At each parameter value, a total of 1024 drips were
recorded, and the interdrip time intervals plotted. The resulting diagram shows a
period-three window, denoted I3, and two other interesting bifurcations denoted
by I and B in the figure.
Event I identifies an interior crisis. As this parameter value is passed, the
dynamical behavior changes from erratic to a period-one rhythm. The average
interdrip time interval does not change appreciably with event I, but is more or
less constant across the break. A scatter plot of (T
n
,T
n⫹1
) changes significantly
as the transition is crossed, as shown in Figure 10.34.
443

S TA B LE M ANIFOLDS AND C RISES
Figure 10.34 Scatter plots of successive time-interval pairs near the interior
crisis.
(a) Complicated dynamics before the crisis parameter value I is followed by simpler
dynamics in (b) and (c) as the flow rate is slowly increased.
Event B identifies a boundary crisis. Now the interdrip time interval changes
abruptly, as a chaotic regime shifts into a periodic cycle of period five. The five
states are close together; the points on the bifurcation diagram to the right of
value B lack sufficient clarity to show the five separate states. Figure 10.35 shows
the transition to a periodic orbit more clearly. Note the abrupt change of average
interdrip time interval from 38.6msecto26.0 msec. This destruction of a basin
of one attractor, resulting in movement to an alternative attractor perhaps far
away in state space, is characteristic of a boundary crisis.
Figure 10.35 Scatter plots near a boundary crisis.
(a) Complicated dynamics before the transition yields to periodic behavior as the
basin boundary of the original attractor is destroyed in (b) and a periodic attractor
results in (c).
444

L AB V ISIT 10
Figure 10.36 Transition from chaotic to periodic pattern.
A motion picture recorded at 30 frames per second shows the change from chaotic
(first five frames) to period-five (last five frames) behavior.
445

C HAPTER E LEVEN
Bifurcations
O
F ALL POSSIBLE motions in dynamical systems, a fixed point or equilibrium is
the simplest. If the fixed point is stable, the system is likely to persist in that state,
even in the face of minor disturbances.
But systems change. Figure 1.6 of Chapter 1 shows that varying the param-
eter in the logistic family from a ⫽ 2.9toa ⫽ 3.1 results in the preferred system
behavior changing from a fixed population to an oscillation between high and
low populations. This change is called a bifurcation. We saw this type of bifur-
cation again in the experiment of Lab Visit 1. Further system parameter changes
are shown to result in even more extreme changes in behavior, including higher
periodicities, quasiperiodicity and chaos. The forced, damped pendulum settles
into periodic motions when the amplitude of the forcing function is small. When
447

B IFURCATIONS
the amplitude is increased to moderate levels, chaotic motions develop. At still
higher amplitudes, periodicity returns.
Just as it is helpful to classify the different types of motion in a system,
it is helpful to categorize the ways that the motion can change as the system
is modified. In fact, as a system parameter varies, these changes cannot occur
capriciously, but only in a limited number of prescribed ways. This limited set
of bifurcations is universal in the sense that it is the same for a large variety of
systems. For this reason, bifurcation theory is a useful and widely studied subfield
of dynamical systems. With the discovery of chaotic dynamics, the theory has
become even more important, as researchers try to find mechanisms by which
systems change from simple to highly complicated behavior. In Chapter 11 we
will describe the most common bifurcations.
11.1 SADDLE-NODE AND PERIOD-DOUBLING
BIFURCATIONS
In Chapter 1 we introduced the one-parameter family of logistic maps g
a
(x) ⫽
ax(1 ⫺ x) and investigated its dynamical properties at various fixed values of the
parameter a. We found that at certain parameter values, including 0 ⬍ a ⬍ 2,
g
a
has a fixed-point attractor; for larger a values, g
a
can have periodic or chaotic
attractors; finally, for a ⬎ 4, the logistic map g
a
has infinitely many periodic
points, but no attracting sets, and almost all orbits diverge to ⫺
⬁
. If fixed points
or periodic points exist at a certain parameter value and not at another, what
has happened to the system at parameter values in between to cause the birth or
death of these orbits? We call a parameter value at which the number or stability
of fixed points or periodic points changes a bifurcation value of the parameter,
and the orbit itself a bifurcation orbit.
Definition 11.1 A one-parameter family of maps on ⺢
n
is a set of maps
f
a
(v), one for each value of a parameter a belonging to an interval I of real
numbers. We refer to ⺢
n
as the state space and to I as the parameter space,and
say f depends on a scalar parameter a 僆 I.
An alternate notation for f
a
(v)isf(a, v), which we use when we want to
emphasize the dependence of the family on the parameter. However, there is a
difference between the parameter a and the state variable v. In order to calculate
an orbit of a map f
a
in such a family, the parameter a is fixed and successive iterates
are calculated in state space for that fixed value of a. We concentrate in particular
448
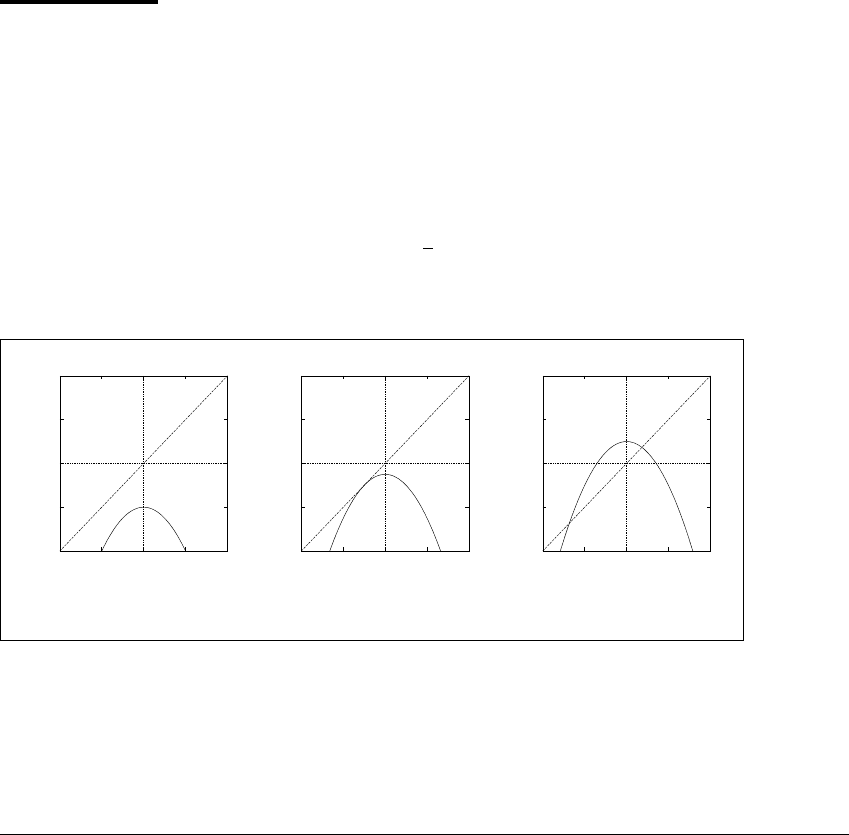
11.1 SADDLE-NODE AND P ERIOD-DOUBLING B IFURCATIONS
on maps with state space ⺢
1
and ⺢
2
. For families of one-dimensional maps, we
write f
a
for the derivative of f
a
with respect to x. For families of two-dimensional
maps, we write Df
a
for the Jacobian matrix of partial derivatives of f
a
taken with
respect to the state space variables (usually x and y).
Two types of bifurcations are most basic. In the first, called a saddle-node
bifurcation, fixed points are born. The second is called a period-doubling bifur-
cation, where a fixed point loses its stability and simultaneously, a new orbit
of doubled period is created. Both of these basic bifurcations occur in the one-
dimensional quadratic family.
E XAMPLE 11.2
Let f
a
(x) ⫽ f(a, x) ⫽ a ⫺ x
2
, where a is a scalar (one-dimensional) param-
eter. When a ⬍⫺1 4, there are no fixed points. At a ⫽⫺1 4, the graph of f
a
is
tangent to the line y ⫽ x. There is exactly one fixed point at x ⫽⫺1 2. For each
a strictly larger than ⫺1 4, the graph of f
a
crosses the line y ⫽ x in two points,
giving rise to two fixed points of f
a
. Figure 11.1 illustrates the three possibilities.
The point (a, x) ⫽ (⫺1 4, ⫺1 2) is a bifurcation point for the map f since the
number of fixed points, as a function of a, changes at a ⫽⫺1 4. When a ⫽ 1 2,
the map f has a repelling fixed point at x ⫽ (⫺1 ⫺
3) 2 and an attracting fixed
-2
-1
0
1
2
-2 -1 0 1 2
-2
-1
0
1
2
-2 -1 0 1 2
-2
-1
0
1
2
-2 -1 0 1 2
(a) (b) (c)
Figure 11.1 A saddle-node bifurcation.
The graph of the quadratic family f(a, x) ⫽ a ⫺ x
2
before, at, and following a saddle-
node bifurcation is shown. (a) At a ⫽⫺1, the graph does not intersect the dotted
line y ⫽ x. (b) At a ⫽⫺0.25, the graph and the line y ⫽ x intersect in one point,
the point of tangency; for a ⬎⫺0.25, they intersect in two points. (c) At a ⫽ 1 2,
f has a repelling fixed point and an attracting fixed point.
449
