Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems
Подождите немного. Документ загружается.


10.3 CRISES
Figure 10.18 A crisis in which a two-piece H
´
enon attractor hits the stable
manifold of a saddle.
The stable manifold of a saddle is shown together with the chaotic attractor for the
same parameters as in Figure 10.17.
➮ COMPUTER EXPERIMENT 10.2
Recreate Figure 10.17 so that each picture includes the plot of only the
even-numbered iterates of some initial point, p, f
2
(p), f
4
(p),....
➮ COMPUTER EXPERIMENT 10.3
Create additional pictures of the two-piece H
´
enon attractor in Figure 10.17.
Then make a graph of the distance between the two pieces as a function of a near
the crisis value. Use this graph to give an estimate of the crisis value.
419

S TA B LE M ANIFOLDS AND C RISES
Other outcomes are possible. If, in particular, p is on the boundary of the
basin of
a
for a ⱕ a
c
(in this case one branch of U(p) is not in the basin of
a
),
we say there is a boundary crisis at a ⫽ a
c
. In this case there are points on U(p)
that go to another attractor (perhaps infinity). Then for a slightly greater than a
c
,
the attractor (and its basin) no longer exist. However, for a only slightly larger
than a
c
, typical orbits spend many iterates on the “ghost” of
a
before escaping to
the other attractor. Figure 10.19 illustrates this phenomenon in the orbit of one
map f
r
for r ⫽ 1.01, in the Ikeda family
f
r
(z) ⫽ r ⫹ 0.9z exp
i
0.4 ⫺
6.0
1 ⫹ |z|
2
,z僆 C,
right after a boundary crisis at r ⫽ r
c
⬇ 1.00. For r ⬍ r
c
, the stable manifold of a
fixed point p (not shown) forms the boundary between the basins of a fixed-point
sink (shown in the upper center of the figure) and another attractor (which is
observed to be chaotic for many r values less than r
c
). In this parameter range,
one branch of
U(p) goes to the chaotic attractor, and the other branch goes to
the fixed-point attractor. For r ⬎ r
c
, the chaotic attractor no longer exists. The
orbit shown in Figure 10.19 spends many iterates on what was the structure of
the chaotic attractor. Then it crosses the stable manifold
S(p) and converges to
7.5
y
⫺4
⫺1.5 x 8
Figure 10.19 Transient chaos.
One orbit of the Ikeda map f
r
(z) ⫽ r ⫹ 0.9ze
i(0.4⫺
6.0
1⫹|z|
2
)
is plotted. The parameter
value is r ⫽ 1.003, immediately following a crisis at which the chaotic attractor
disappears. The orbit spends many iterates on the “ghost” of what was the chaotic
attractor before escaping and converging to a fixed-point attractor. The closer the
parameter to the crisis value, the longer the orbit appears to be chaotic.
420
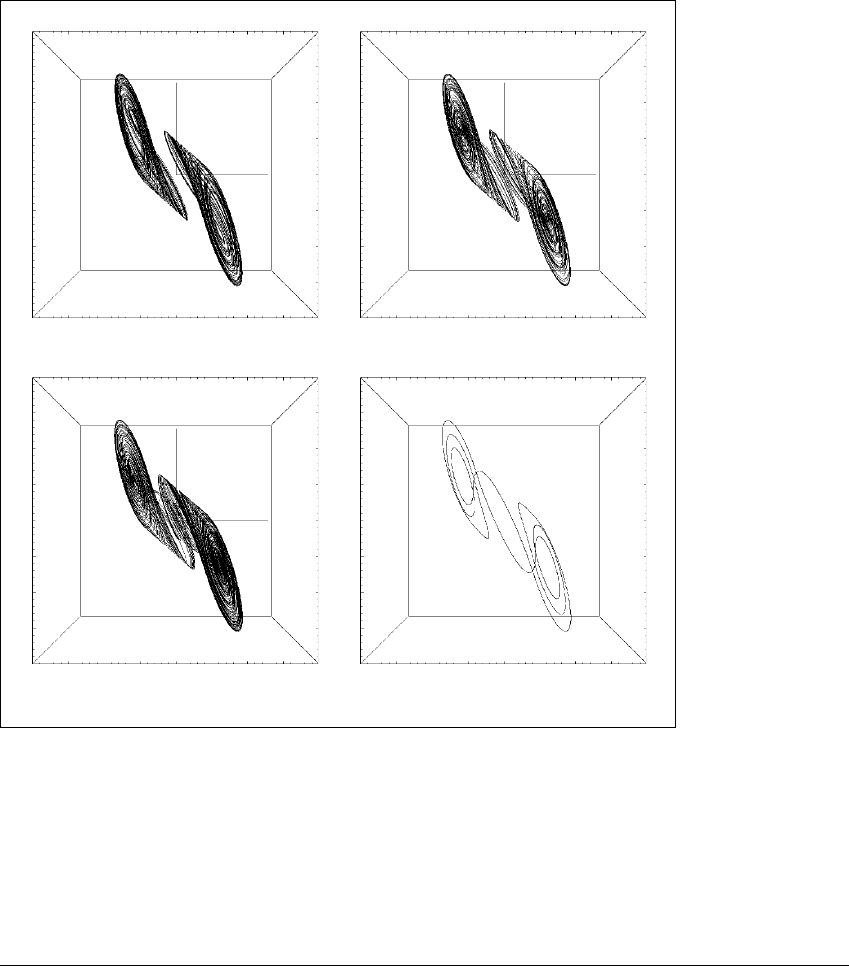
10.3 CRISES
the fixed-point attractor. This behavior is called transient chaos. The closer the
parameter to the crisis value, the longer the orbit appears to be chaotic. See Figure
9.5 for an example of transient chaos in the Lorenz attractor.
As a final example, Figure 10.20 illustrates crises in the Chua circuit system
(9.6). The crises are described as a parameter a is decreased. In (a) there are two
(a) (b)
(c) (d)
Figure 10.20 Interior crisis and boundary crisis in the Chua circuit.
Fixed parameters are c
1
⫽ 15.6, c
2
⫽ 1, m
0
⫽⫺8 7, m
1
⫽⫺5 7. The attracting
set changes as parameter c
3
changes. (a) c
3
⫽ 32, two coexisting chaotic attractors
with separate basins. (b) c
3
⫽ 31.5, the attractors move toward one another, but
do not yet touch (although their projections to the plane overlap). (c) c
3
⫽ 31,
the attractors have merged into a single attractor. (d) c
3
⫽ 30, a boundary crisis
has caused a periodic orbit to attract the basin of the previous chaotic double-scroll
attractor. As c
3
is decreased further, the double-scroll attractor reappears.
421

S TA B LE M ANIFOLDS AND C RISES
distinct chaotic attractors, which approach each other in (b) (overlapping only
in the two-dimensional projection), and then merge in (c). Due to symmetries in
the system, this crisis is similar to the interior crisis of the H
´
enon family shown
in Figure 10.17. A boundary crisis follows, where the chaotic (double scroll)
attractor moves into the basin of a periodic attractor, as shown in (d).
One-dimensional families can also undergo crises as a parameter is varied.
See, for example, Figure 6.3(a), the bifurcation diagram of the logistic family.
(Several other bifurcation diagrams appear in Chapters 11 and 12.) Chaotic
attractors are observed to jump in size or suddenly appear or disappear. For one-
dimensional maps, basin boundary points are repelling fixed points or periodic
points or pre-images of these points. Interior and boundary crises occur as an
attractor collides with a repelling fixed point or periodic orbit. For example, in
the logistic family g
a
(x) ⫽ ax(1 ⫺ x), 1 ⱕ a ⱕ 4, the points x ⫽ 0andx ⫽ 1
form the boundary between points with bounded orbits and those in the basin
of infinity. At a ⫽ 4 the chaotic attractor has grown to fill the unit interval and
contains these boundary points. For a ⬎ 4, there are no (finite) attractors. Thus
there is a boundary crisis at a ⫽ 4.
10.4 PROOF OF THE STABLE
MANIFOLD THEOREM
A fixed-point saddle of a planar diffeomorphism has a stable manifold and an
unstable manifold, which are smooth one-dimensional curves (that is, one-
manifolds). In this section we prove that the stable manifold is a one-dimensional
curve, although we do not discuss its smoothness. The proof of smoothness is rather
technical and is not within the scope of this book. We direct the interested reader
to (Devaney, 1986). The existence of the unstable manifold as a one-dimensional
curve follows by applying the result to the inverse of the map.
Recall that a point v ⫽ (x
1
,x
2
) is in the stable manifold of a fixed point p ⫽
(p
1
,p
2
)iff
n
(v) → p as n →
⬁
. As Figure 10.21 illustrates, given a neighborhood
B of p, the stable manifold may enter and leave B many times. In fact, when there
is a homoclinic point, the stable manifold S (p) intersects B in infinitely many
pieces. We focus on the one piece of the intersection which contains p, and call
this (connected) piece the local stable manifold of p in B. We will show in the
proof of the Stable Manifold Theorem that there exists a neighborhood B such
422
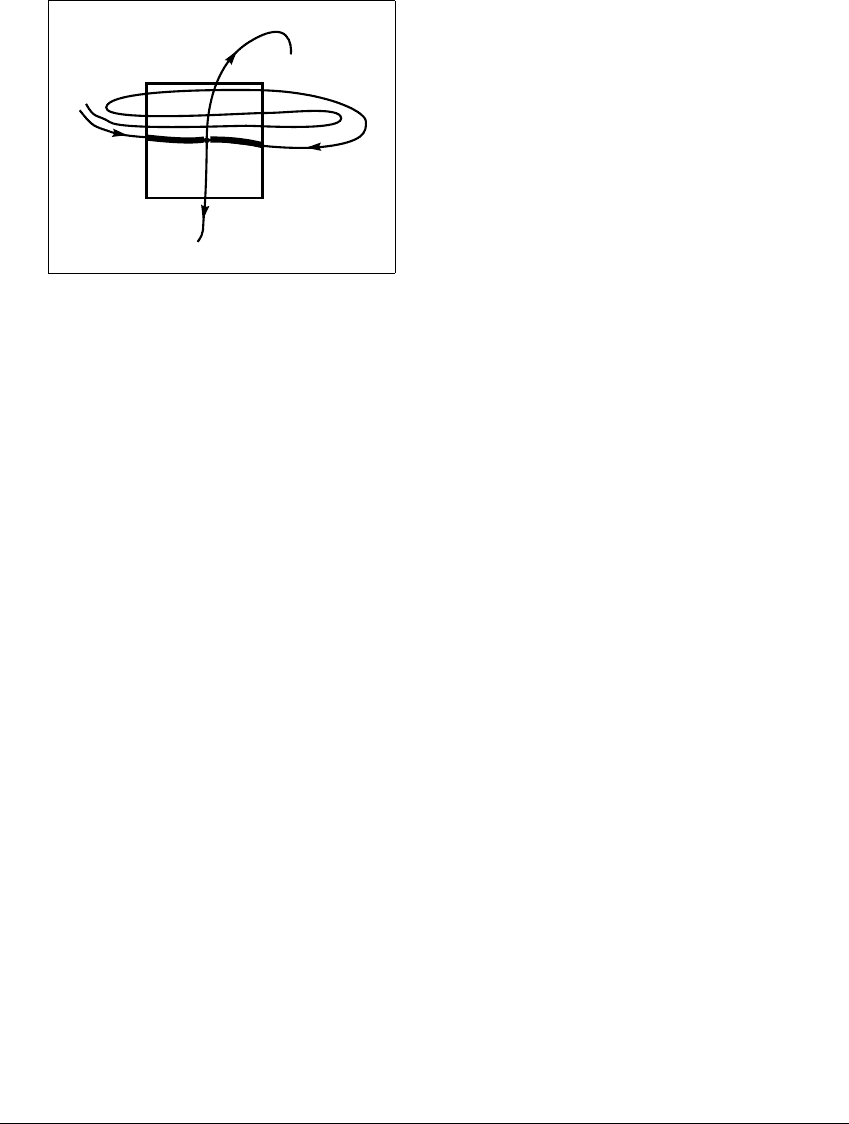
10.4 PROOF OF THE S TA BLE M ANIFOLD T HEOREM
S
B
B
Figure 10.21 The local stable manifold.
For a sufficiently small neighborhood B of p, the local stable manifold
S
B
is the set
of points v in the stable manifold of p such that f
n
(v)isinB, for all n ⫽ 0, 1, 2,....
that the local stable manifold of p in B can be characterized as the set
S
B
⫽ 兵v : f
n
(v) 僆 B, for all n ⫽ 0, 1, 2,..., and f
n
(v) → p其,
that is, the set of points whose entire forward orbits remain in B and tend to P.
For the purposes of this proof, we call the set
S
B
the local stable set of p in B, and
show that it has the properties desired of the local stable manifold.
To analyze the behavior near a saddle, we choose coordinates so that (0, 0)
is the fixed point, and (1, 0) and (0, 1) are eigenvectors of Df(0). The eigenvector
(1, 0) has eigenvalue s, with |s| ⬍ 1, and (0, 1) has eigenvalue u,with|u| ⬎ 1.
We prove the following restatement of Theorem 10.1. Recall that a map f is called
“twice differentiable” if all the first- and second-order partial derivatives of f exist
and are continuous.
Theorem 10.10 Let f be a diffeomorphism of the plane that is twice differen-
tiable. In the coordinate system given above, there exists a number
␦
⬎ 0 and a square
neighborhood B ⫽ [⫺
␦
,
␦
] ⫻ [⫺
␦
,
␦
] of (0, 0) in which the local stable set S
B
of (0, 0)
is given by the graph of a continuous function; that is, there is a continuous function
on [⫺
␦
,
␦
] such that
S
B
⫽ 兵(x,
(x)) : x 僆 [⫺
␦
,
␦
]其.
Furthermore,
(0) ⫽ 0.
Theorem 10.10 says that the curve
S
B
extends through a neighborhood
of (0, 0). In order to show that the entire stable manifold is a curve (with no
423

S TA B LE M ANIFOLDS AND C RISES
self-intersections and no endpoints), see Exercise 10.6. The proof of Theorem
10.10 is given in seven lemmas. In the first, we choose a square neighborhood
of the origin on which we can estimate how much the function differs from its
derivative.
From our hypothesis, Df(0) ⫽
s 0
0 u
. Call this matrix A. Since
f(p) ⫺ f(0) ⬇ Df(0)(p)andf(0) ⫽ 0,
we can say that f(p) is approximated by Ap. We now choose a square centered
at the origin to be small enough that Ap is a good approximation to f(p)and
A(q ⫺ p) is a good approximation to f(q) ⫺ f(p).
Lemma 10.11 For any
⑀
⬎ 0, there is a
␦
⬎ 0suchthat
|f(q) ⫺ f(p) ⫺ A(q ⫺ p)| ⱕ
⑀
|q ⫺ p|,
for all p, q in the box B ⫽ [⫺
␦
,
␦
] ⫻ [⫺
␦
,
␦
].
This result should seem quite reasonable to the reader. The proof, however,
is quite technical. We recommend postponing a careful reading of the proof until
the structure of the proof is clear. (In fact, we recommend skipping all proofs on
first reading of this chapter.)
Proof: We can estimate how f(q) ⫺ f(p) compares with q ⫺ p, provided
p and q are close to the origin. From the two-dimensional Taylor’s Theorem, we
have
|f(q) ⫺ f(p) ⫺ Df(p)(q ⫺ p)| ⱕ C
1
|q ⫺ p|
2
,
for some positive constant C
1
. Since f is twice differentiable, the matrix Df(p),
which is the derivative of f at p, and the derivative Df(0) differ by a matrix whose
norm (and the entries in the matrix) differ by a quantity at most proportional to
|p ⫺ 0| ⫽ |
|. That is,
|Df(p)(q ⫺ p) ⫺
s 0
0 u
(q ⫺ p)|
ⱕ
Df(p) ⫺
s 0
0 u
|q ⫺ p|
ⱕ C
2
|p||p ⫺ q|,
424
10.4 PROOF OF THE S TA BLE M ANIFOLD T HEOREM
for some positive constant C
2
. Hence
f(q) ⫺ f(p) ⫺
s 0
0 u
(q ⫺ p)
ⱕ C
2
|p||p ⫺ q| ⫹ C
1
|p ⫺ q|
2
⫽ |p ⫺ q|
C
2
|p| ⫹ C
1
|p ⫺ q|
. (10.3)
Let B be the square [⫺
␦
,
␦
] ⫻ [⫺
␦
,
␦
]. Then for p and q in the square B,
the right-hand side multiplier of |p ⫺ q| in Equation (10.3) is no bigger than
2
2C
1
␦
⫹
2C
2
␦
. We choose
␦
small enough that this quantity is less than
⑀
.
We now have a bound on how much f(p) ⫺ f(q) can differ from the linear
approximation A(p ⫺ q), for p and q in B. For the remainder of the proof assume
that p and q are points in B. We use subscripts to denote the x-andy- coordinates
of vectors; (q ⫺ p)
x
and (q ⫺ p)
y
mean, respectively, the x-andy- coordinates of
q ⫺ p.
We say p and q are horizontally aligned if
|
(q ⫺ p)
x
|
ⱖ
(q ⫺ p)
y
and vertically aligned if
|
(q ⫺ p)
x
|
ⱕ
(q ⫺ p)
y
.
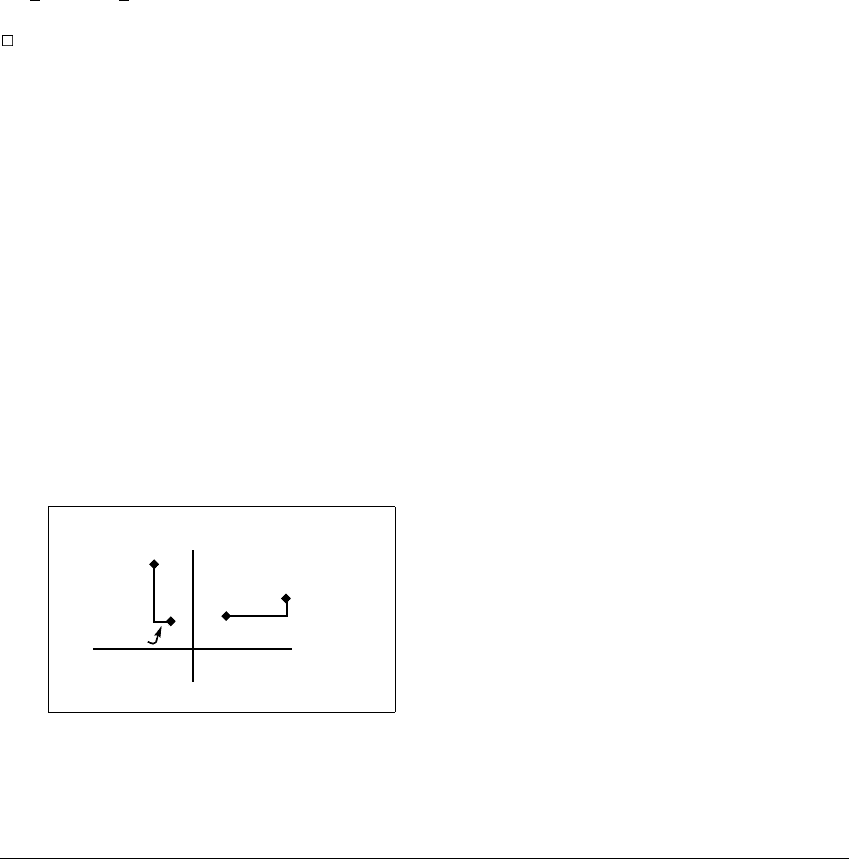
In Figure 10.22 the points p and q are horizontally aligned and points r and s are
vertically aligned. We will assume throughout the remainder of this section that
x
y
r
s
q
p
|(q - p)
y
|
|(q - p)
x
|
|(r - s)
x
|
|(r - s)
y
|
Figure 10.22 Horizontal and vertical alignment.
The points s and r are vertically aligned since the x-component of r ⫺ s is smaller
than the y-component; the points p and q are horizontally aligned since the y-
component of p ⫺ q is smaller than the x-component.
425

S TA B LE M ANIFOLDS AND C RISES
the eigenvalues u and s are positive. The proofs of the remaining lemmas can be
adapted easily for the general case.
In Lemma 10.12, we show that there is a neighborhood B of the origin
such that if two points are vertically aligned and in B, then their images are also
vertically aligned.
Lemma 10.12 Let
ˆ
u ⫽
u⫹1
2
⬎ 1and
ˆ
s ⫽
s⫹1
2
⬍ 1. There exists a square
neighborhood B of (0, 0), B ⫽ [⫺
␦
,
␦
] ⫻ [⫺
␦
,
␦
], such that the following prop-
erties hold for all p, q 僆 B:
1. If p and q are vertically aligned, then
(f(q) ⫺ f(p))
y
ⱖ
ˆ
u
(q ⫺ p)
y
.
2. If p and q are horizontally aligned, then |(f(q) ⫺ f(p))
x
| ⱕ
ˆ
s|(q ⫺ p)
x
|.
3. If p and q are vertically aligned, then so are f(p)andf(q).
Before studying the proof, the reader should first check that (1), (2), and
(3) hold in the special case f(p) ⫽ Ap, and that they also hold if f(p) ⫽ A
1
p, for
a matrix A
1
sufficiently close to A.
Proof: Let
⑀
⬍ min兵
u⫺1
2
,
1⫺s
2
其, and let
␦
and B be given (for this
⑀
, as
in Lemma 10.11). Notice with this choice of
⑀
⬎ 0thatu ⫺
⑀
2 ⬎
ˆ
u and
s ⫹
⑀
2 ⬍ 1.
We begin with the proof of (1). Lemma 10.11 implies that each coordinate
of f(q) ⫺ f(p) differs from (s(q ⫺ p)
x
,u(q ⫺ p)
y
)byatmost
⑀
q ⫺ p. We assume
p ⫽ q. Since p and q are vertically aligned, it differs by at most
⑀
2 |(q ⫺ p)
y
|.
Therefore,
|u(q ⫺ p)
y
| ⫺ |(f(q) ⫺ f(p))
y
| ⱕ |u(q ⫺ p)
y
⫺ (f(q) ⫺ f(p))
y
|
ⱕ
⑀
2 |(q ⫺ p)
y
|,
which implies
|(f(q) ⫺ f(p))
y
| ⱖ u|(q ⫺ p)
y
| ⫺
⑀
2 |(q ⫺ p)
y
|
⫽ (u ⫺
⑀
2)|(q ⫺ p)
y
|
⬎
ˆ
u|(q ⫺ p)
y
|.
The second inequality follows from the choice of
⑀
. The proof of (2) is similar.
426

10.4 PROOF OF THE S TA BLE M ANIFOLD T HEOREM
To prove (3), we continue to assume that p and q are vertically aligned and
refer to (1). Then
|(f(q) ⫺ f(p))
x
| ⫺ s|(q ⫺ p)
x
| ⱕ |(f(q) ⫺ f(p))
x
⫺ s(q ⫺ p)
x
|
ⱕ
⑀
2 |(q ⫺ p)
y
|,
which implies
|(f(q) ⫺ f(p))
x
| ⬍ s|(q ⫺ p)
x
| ⫹
⑀
2|(q ⫺ p)
y
|
ⱕ s|(q ⫺ p)
y
| ⫹
⑀
2|(q ⫺ p)
y
|
ⱕ (s ⫹
⑀
2)|(q ⫺ p)
y
|
⬍ |(q ⫺ p)
y
|
⬍
ˆ
u|(q ⫺ p)
y
|
ⱕ |(f(q) ⫺ f(p))
y
|.
Therefore, f(q)andf(p) are vertically aligned.
In Lemmas 10.13–10.16, let B be defined as in Lemma 10.12.
Lemma 10.13 If f
n
(p)isinB for all n ⫽ 0, 1, 2,..., then p is in the
local stable set
S
B
.
Proof: We need to show that f
n
(p) → 0, as n →
⬁
. If p ⫽ 0, we are
done. Thus assume p ⫽ 0. First, we argue that f
n
(p)and0 are horizontally
aligned for all n ⬎ 0. Suppose otherwise: Assume there exists a k such that f
k
(p)
and 0 are vertically aligned. Since p ⫽ 0, f
k
(p)
y
⫽ 0, and by Lemma 10.12 (1),
|f
m
(p)
y
| ⬎
ˆ
u
m⫺k
|f
k
(p)
y
|, for all m ⬎ k. Hence |f
m
(p)
y
| →
⬁
as m →
⬁
. But f
n
(p)
is in B, for all n, a contradiction. Thus f
n
(p)and0 are horizontally aligned, for
all n.
Now, by Lemma 10.12(2), |f
n
(p)
x
| → 0. Since f
n
(p)and0 are horizontally
aligned, |f
n
(p)
x
| ⱖ |f
n
(p)
y
| ⱖ 0, for each n. Therefore, f
n
(p) → 0. .
Lemma 10.14 Every pair of points in
S
B
is horizontally aligned.
Proof: Let p and q be in
S
B
. Suppose instead that p and q are vertically
aligned. Then, by Lemma 10.12 (1) and (3), the y-coordinates of forward iterates
of p and q separate until at least one orbit leaves B, contradicting the definition
of
S
B
.
427
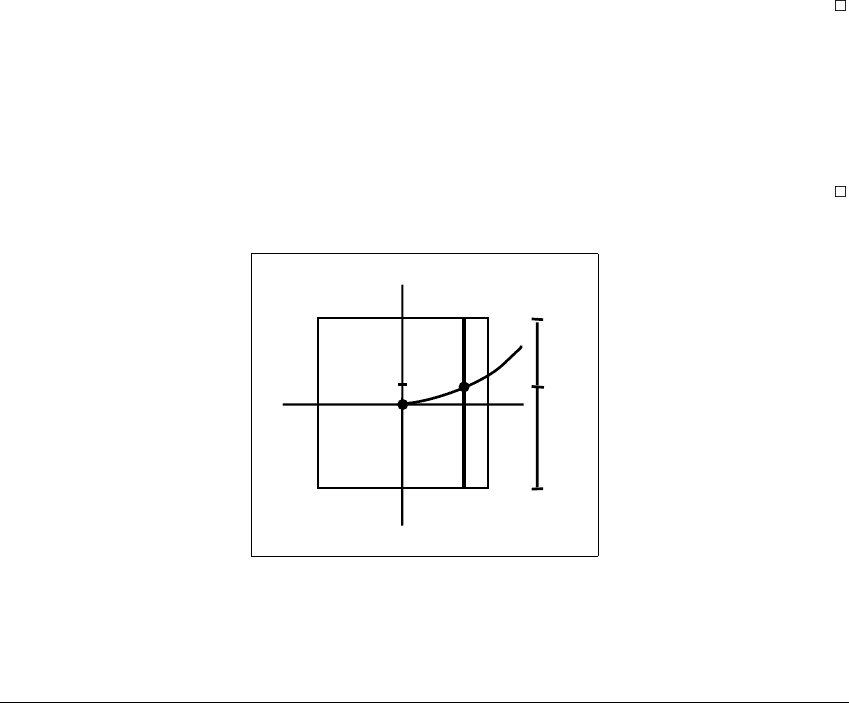
S TA B LE M ANIFOLDS AND C RISES
Lemma 10.15 For each x in [⫺
␦
,
␦
], there is exactly one value y ⫽
(x)
such that (x,
(x)) is in S
B
.
Proof: Let L
x
⫽ 兵(x, y):⫺
␦
⬍ y ⬍
␦
其 傺 B be the vertical line segment
through x, as shown in Figure 10.23. Let T
x
be the set of points in L
x
whose
orbits eventually leave B through the top of B, (whose y-coordinates become
greater than
␦
), and let B
x
be the set of points in L
x
whose orbits eventually leave
B through the bottom of B, (whose y-coordinates become smaller than ⫺
␦
).
Notice that T
x
and B
x
are both nonempty. Then if p is in T
x
, there is an
⑀
⬎ 0
such that points in N
⑀
(p) 傽 L
x
are also in T
x
. Therefore, T
x
is the union of a
finite number of open intervals. So is B
x
.SinceT
x
and B
x
are disjoint, there must
be a point q in L
x
such that q is neither in T
x
nor in B
x
. (For example, we could
take q ⫽ inf T
x
.)
Now all points whose orbits leave B must leave through the top or bottom.
Therefore, f
n
(q) 僆 B, for all n ⬎ 0. By Lemma 10.13, q is in S
B
. From Lemma
10.14, there is only one point on L
x
whose orbit stays in B.Let
(x) ⫽ q
y
.
Lemma 10.16 The function
is continuous.
Proof: Let a be a number in [⫺
␦
,
␦
]. Suppose lim
x→a
(x) ⫽
(a). Then
there exists
⑀
⬎ 0 and a sequence x
n
→ a such that |
(x
n
) ⫺
(a)| ⬎
⑀
, for each
n. Let x
k
be an element of the sequence such that |x
k
⫺ a| ⬍
⑀
. Then (x
k
,
(x
k
))
and (a,
(a)) are not horizontally aligned, contradicting Lemma 10.14.
T
x
B
x
x
q
L
x
B
Figure 10.23 Illustration for the Proof of Lemma 10.15.
Points on the vertical line segment L
x
through x are either in T
x
, if the orbit of the
point leaves the box B through the top, or in B
x
, if it leaves through the bottom.
The point q stays in B for all forward iterates.
428
