Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

10.2 HOMOCLINIC AND H ETEROCLINIC P OINTS

than 10

⫺12

. Usually 10

⫺4

is smaller than the diameter of a dot. Ignoring the “10

rule”, however, will probably give excellent longer plots. Also, the use of 10

⫺6

and

⫺12

are very conservative; in practice, one can usually use |a ⫺ b| ⬇ 0.1. This

method is most successful when the unstable manifold is bounded; reﬁnements

are necessary otherwise. See (You, Kostelich, and Yorke, 1991).

10.2 HOMOCLINIC AND HETEROCLINIC

POINTS

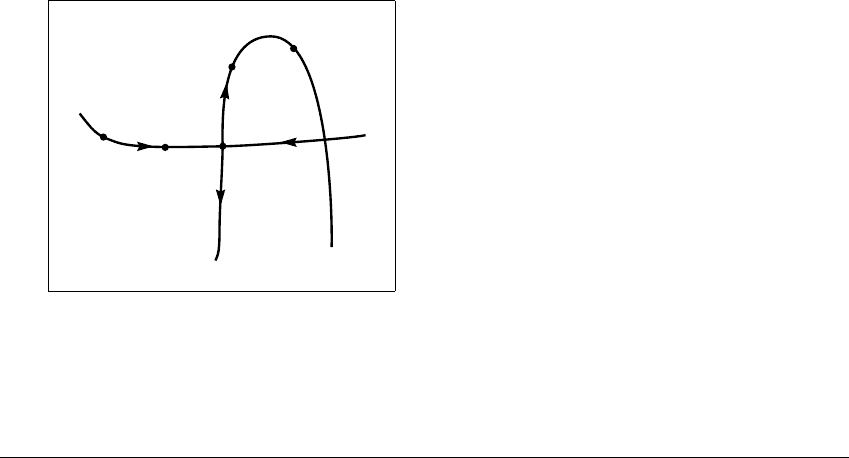
At ﬁrst glance, the picture of crossing stable and unstable manifolds shown in

Figure 10.9 looks bizarre, if not impossible. Perhaps drawing the manifolds as

curves makes us incorrectly think of them as solutions of differential equations

which, by uniqueness of solutions through a given point (Theorem 7.14 of Chapter

7), can never cross. For diffeomorphisms, however, stable and unstable manifolds

are each composed of inﬁnitely many orbits, some of which can belong to both

invariant manifolds. Suppose, for example, that x is a point belonging to both

the stable and unstable manifolds of a ﬁxed point p. According to the deﬁnitions,

both forward and backward iterates of x converge to p.

Deﬁnition 10.6 Let f be an invertible map of ⺢

, and let p be a ﬁxed

point saddle. A point that is in both the stable and the unstable manifold of p

and that is distinct from p is called a homoclinic point.Ifx is a homoclinic point,

f(r)

f(q)

Figure 10.9 Crossing stable and unstable manifolds.

The stable manifold

S and unstable manifold U of a saddle ﬁxed point or periodic

point p cross at a homoclinic point x. If q is a point on

S, then f(q)isalsoonS;if

r is a point on

U, then f(r)isalsoonU. The “homoclinic” point x is on both S

and U.

409

S TA B LE M ANIFOLDS AND C RISES

then f

(x) → p and f

⫺n

(x) → p, as n →

⬁

. The orbit of a homoclinic point is

called a homoclinic orbit. A point in the stable manifold of a ﬁxed point p and

in the unstable manifold of a different ﬁxed point q is called a heteroclinic point.

The orbit of a heteroclinic point is called a heteroclinic orbit.

✎ E XERCISE T10.2

Show that homoclinic points map to homoclinic points under f and f

⫺1

The existence of homoclinic orbits has complex and profound conse-

quences. We explore a few of these consequences in the remainder of this section.

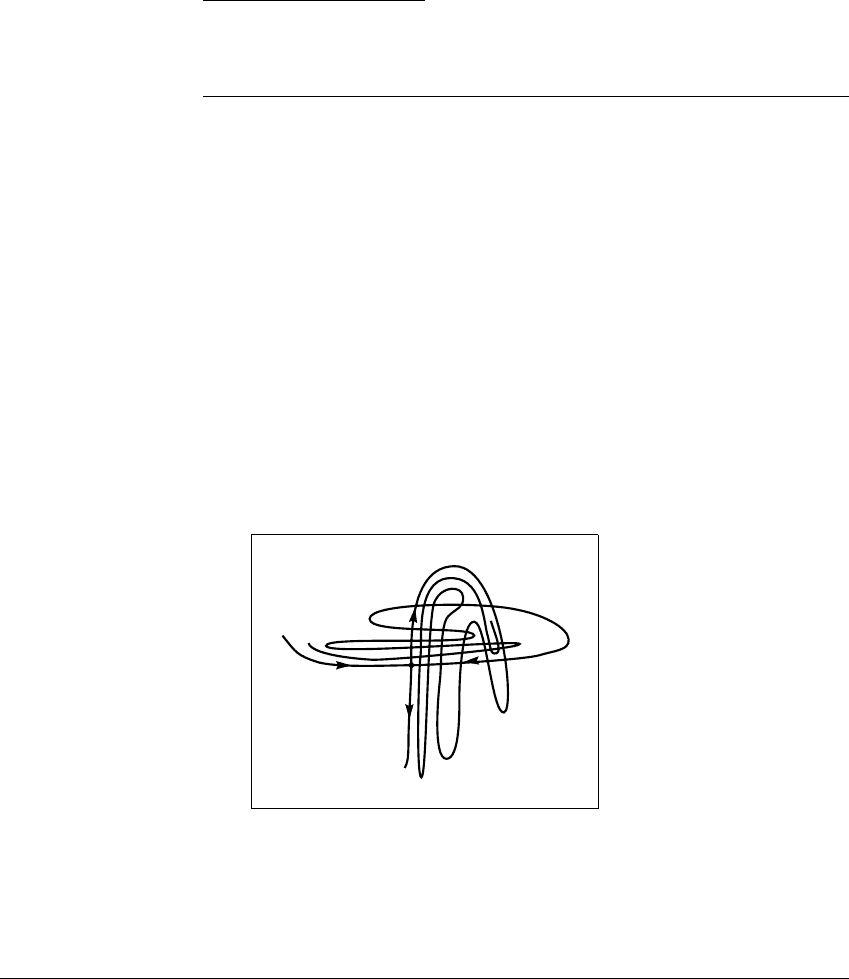
A point where stable and unstable manifolds cross maps to another such point;

its pre-image is also a crossing point. We can only begin to indicate the intricate

web of these crossings, as in Figure 10.10. Certainly Poincar

e appreciated the

complicated dynamics implied here. S. Smale’s celebrated work on the horseshoe

map in the 1960s (Smale, 1967) greatly simpliﬁed the understanding of these

dynamics.

In Chapter 5 we described the prototype or ideal horseshoe map. In that

discussion we alluded to the fact that in order for a map of the plane, such as the

enon map, to have exactly the dynamics of the ideal horseshoe, there must be

uniform stretching and contraction at points in the invariant set. Smale showed

that the presence of homoclinic points implies the existence of a hyperbolic

Figure 10.10 Tangle of stable and unstable manifolds implied by homoclinic

points.

If the stable and unstable manifolds of a ﬁxed-point saddle or periodic point p cross

in one homoclinic point, then they cross inﬁnitely many times: each forward and

backward iterate of a homoclinic point is a homoclinic point.

410

10.2 HOMOCLINIC AND H ETEROCLINIC P OINTS

horseshoe, a horseshoe that is identical (after a change in coordinates) to the

one in Chapter 5. In particular, the set of points that remain in the horseshoe

under both forward and backward iteration of the appropriate map is a Cantor

set, an uncountable set with no connected subsets (except individual points).

This invariant Cantor set will be in one-to-one correspondence with the set of

bi-inﬁnite binary sequences, as in Chapter 5.

The construction of a horseshoe near a homoclinic orbit is indicated in

Figure 10.11. Start with a box R containing a ﬁxed point p of an invertible

map f. Under iterates of f,Rstretches out along the unstable manifold of p;under

iterates of f

⫺1

, it stretches out along the stable manifold. In particular, there are

numbers l and k such that f

⫺l

(R) extends along the stable manifold to include a

homoclinic point x, and f

(R) extends along the unstable manifold to include x,

as shown in Figure 10.11. Thus f

k⫹l

is a horseshoe map with domain f

⫺l

(R)and

its image f

(R). Geometrically, this construction is clear. What is not so easy to

see is just how small R and how large k and l must be in order to have the uniform

contraction and expansion necessary for a hyperbolic horseshoe.

We summarize Smale’s result in Theorem 10.7. A stable manifold and an

unstable manifold are said to cross transversally if the two manifolds intersect

with a positive angle between them; if the angle between lines tangent to the

two manifolds at the point of crossing is nonzero. If the curves are tangent at

their crossing, then the angle between them is zero and the curves do not cross

transversally. Figure 10.12 illustrates transversal and nontransversal intersections.

-l

(R)

Figure 10.11 Construction of a horseshoe near a homoclinic point.

The stable and unstable manifolds of a saddle p intersect in a homoclinic point x.

A rectangle R is centered at p. Then for some positive integers k and l, k forward

iterates of R and l backward iterates of R intersect at x, so that f

k⫹l

forms a horseshoe.

411

S TA B LE M ANIFOLDS AND C RISES

Figure 10.12 Transversal and nontransversal crossings of stable and unstable

manifolds.

The crossing at x

is a transversal crossing, while the crossing at x

is not, since the

stable and unstable manifolds have the same tangent line at x

Theorem 10.7 Let f be a diffeomorphism of the plane, and let p be a ﬁxed

point saddle. If the stable and unstable manifolds of p cross transversally, then there is

a hyperbolic horseshoe for some iterate of f.

Many of the computer representations of stable and unstable manifolds

in this book indicate homoclinic points. Figure 10.1 shows apparent transversal

crossings of the manifolds in the time-2

␲

map of the forced, damped pendulum.

They are also apparent in the time-2

␲

map of the forced, damped Dufﬁng system,

as described in the following example.

E XAMPLE 10.8

We return to the Dufﬁng equation of Example 10.4—this time adding

damping, and then external forcing, to the system. Figure 10.13 shows the stable

and unstable manifolds of a saddle ﬁxed point under the time-2

␲

mapofthe

damped Dufﬁng equation

x ⫹ 0.1

x ⫺ x ⫹ x

⫽ g(t), (10.2)

ﬁrst with no external forcing (g (t) set equal to 0) in (a), and then with g(t) ⫽

0.3sint in (b). In the presence of damping (represented by the nonzero

x term),

the connecting arcs of the undamped system (Figure 10.6) have split into dis-

tinct stable and unstable manifolds. With g(t) ⫽ 0, each branch of the unstable

manifold of 0 spirals into one of two ﬁxed point sinks.

412

10.3 CRISES

(a) (b)

Figure 10.13 Stable and unstable manifolds for the time-2

␲

map of the

damped and periodically forced Dufﬁng equation.

(a) Motion is governed by the autonomous equation

x ⫹ 0.1

x ⫺ x ⫹ x

⫽ 0. Stable

and unstable manifolds of the ﬁxed point 0 (marked with a cross) under the time-2

␲

map are shown. Each branch of the unstable manifold converges to one of two ﬁxed

point sinks. The stable manifold of 0 forms the boundary between the basins of

attraction of these sinks. In (b) stable and unstable manifolds cross, as an external

force is added to the system, now governed by the equation

x ⫹ 0.1

x ⫺ x ⫹ x

⫽

0.3sint. The ﬁxed point saddle (marked with a cross) has moved from the origin.

When a periodic force g(t) ⫽ 0.3sint is applied to the system, orbits that

previously converged to the sinks may no longer converge. Figure 10.13(b) shows

the stable and unstable manifolds of a saddle ﬁxed point (moved slightly from the

origin shown in (a)), which appear to cross transversally at transverse homoclinic

points. By Theorem 10.7, these points imply the system has chaotic orbits. A

numerically observed chaotic attractor for this system is shown in Chapter 9.

10.3 CRISES

Much of the theory of dynamical systems describes changes that can occur in

the dynamics as a parameter is varied past critical values. How are the signiﬁ-

cant features of a dynamical system affected when the system undergoes a slight

perturbation—as, for example, when the parameters in a map are varied? A hy-

perbolic ﬁxed point may move slightly, but it will persist as long as it remains

413

S TA B LE M ANIFOLDS AND C RISES

hyperbolic. In this section, we turn our attention to chaotic attractors and show

how small variations in a map can result in sudden drastic changes in an attrac-

tor. These changes are called crises and can include the sudden appearance or

disappearance of the attractor or a discontinuous change in its size or shape.

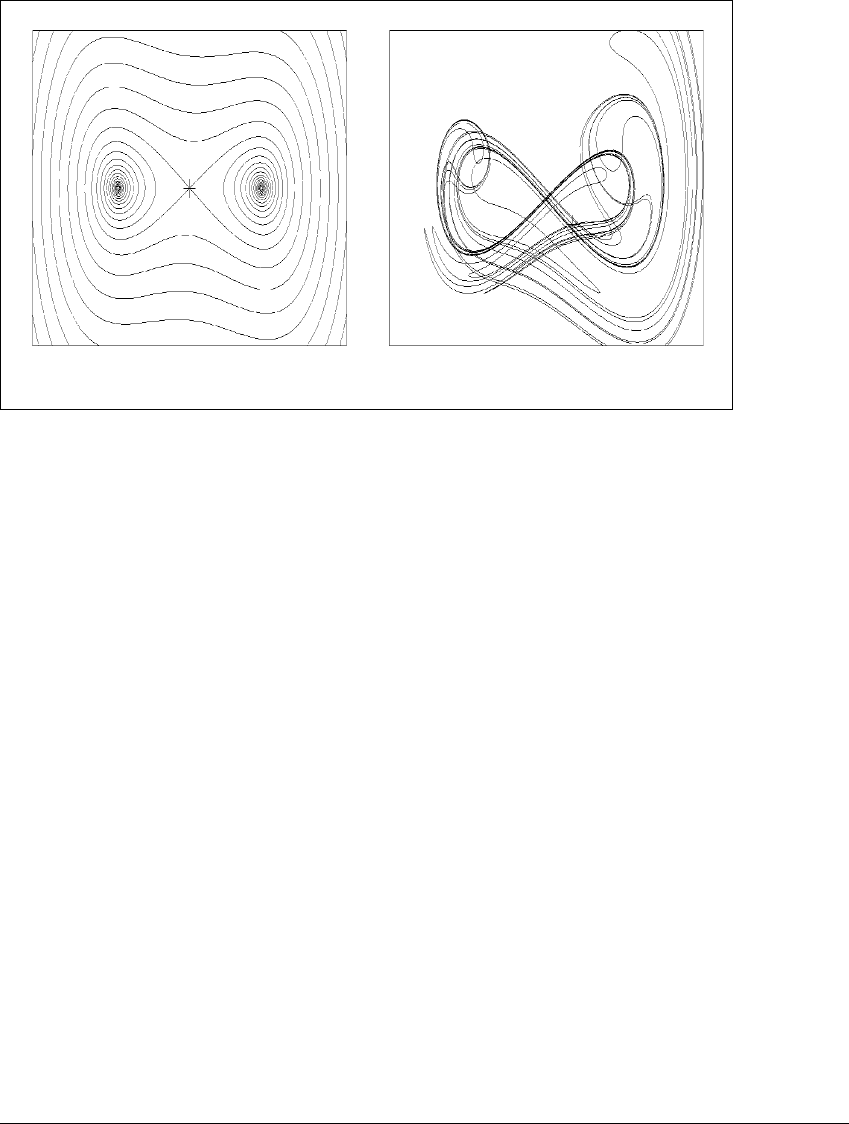
Figure 10.14 shows numerically observed chaotic attractors for the one-

parameter Ikeda family

(z) ⫽ 0.84 ⫹ 0.9z exp





0.4 ⫺

1 ⫹ |z|





,z僆 C,

at a ⫽ 7.1 in (a) and a ⫽ 7.3 in (b). The key to writing this map in (x, y)-

coordinates (where z ⫽ x ⫹ iy) is to use the fact that e

⫽ cos r ⫹ i sin r, for any

real number r.

✎ E XERCISE T10.3

Find the inverse of f

(z).

The shape of the attractor varies only slightly from that shown in (a) for

a in the range 7.1 ⬍ a ⱕ a

⬇ 7.24. For a ⬎ a

, however, the attractor in this

(a) (b)

Figure 10.14 Chaotic attractor of the Ikeda map.

The shape of the attractor observed for a range of parameters up to and including

the crisis value a ⫽ a

is shown in (a). For all a strictly greater than and near a

,the

attractor is signiﬁcantly larger, as shown in (b). Notice that the attractor in (b) has

a dark central part that is similar to the attractor in (a).

414

10.3 CRISES

region of the plane is suddenly much larger. Figure 10.14(b) shows the extent of

the larger attractor for a ⫽ 7.3.

➮ COMPUTER EXPERIMENT 10.1

Create at least six additional plots of the chaotic attractor of the Ikeda map

for six values of a near a

. Plot 10

points of a trajectory on the attractor for each.

Then describe what you can see concerning how the smaller attractor in Figure

10.14(a) changes discontinuously into the larger one in (b). Warning: there is

another attractor—a ﬁxed point.

The structure of the smaller attractor is still apparent in Figure 10.14(b).

It appears darker, since orbits spend a larger percentage of iterates in this region.

Surprisingly, the attractor does not continuously increase in size as a passes a

The closer a ⬎ a

is to the crisis parameter value a

, however, the longer orbits

typically stay on the smaller structure before bursting free. The time the trajectory

stays in the new region is largely independent of a for a ⫺ a

small.

What happens at a crisis value, such as a

in this example? We observe

a saddle periodic orbit p that exists for all a near a

: for a ⬍ a

, this periodic

orbit is not in the attractor

␪

, but as a approaches a

(from below), the distance

between them goes to 0, and at a ⫽ a

, the attractor and the periodic orbit collide.

The periodic orbit is in no way affected by this collision. To understand why the

attractor in our example suddenly increases in size for a ⬎ a

, we want to examine

carefully what happens when the attractor crosses a stable manifold—in this case,

the stable manifold of the orbit p. This step is provided by Theorem 10.9. Recall

that one curve crosses another transversally if the angle between them at the

point of intersection is nonzero.

Theorem 10.9 (The Lambda or Inclination Lemma.) Let f be a diffeomor-

phism of the plane, and let p be a hyperbolic ﬁxed-point saddle of f. Suppose that a

curve L crosses the stable manifold of p transversally. Then each point in the unstable

manifold of p is a limit point of



n⬎0

(L).

The proof of Theorem 10.9 can be found, for example, in (Palis and de

Melo, 1982). When L is a segment of the unstable manifold itself, for example

when there is a transverse crossing of the stable and unstable manifolds of p,

then Theorem 10.9 says that each segment of

U(p) has other segments of U(p)

415

S TA B LE M ANIFOLDS AND C RISES

(L)

f(L)

(L)

Figure 10.15 Illustration of the Lambda Lemma.

A curve L crosses the stable manifold of p transversally. Forward iterates of L limit

on the entire unstable manifold of p. Speciﬁcally, the Lambda Lemma says that for

each point q on the unstable manifold of p and for each

⑀

-neighborhood N

⑀

(q),

there are points of f

(L)inN

⑀

(q), if n is sufﬁciently large.

limiting on it (see Figure 10.15). Speciﬁcally, the Lambda Lemma says that for

each point q on the unstable manifold of p and for each

⑀

-neighborhood N

⑀

(q),

there are points of f

(L)inN

⑀

(q), if n is sufﬁciently large. Of course, in this case,

each f

(L) is a different segment of U(p). Recall that each point in a Cantor set

is a limit point of (other points in) the set. Hence, typical cross sections of the

unstable manifold will have a Cantor set structure. An analogous result holds for

curves that cross the unstable manifold.

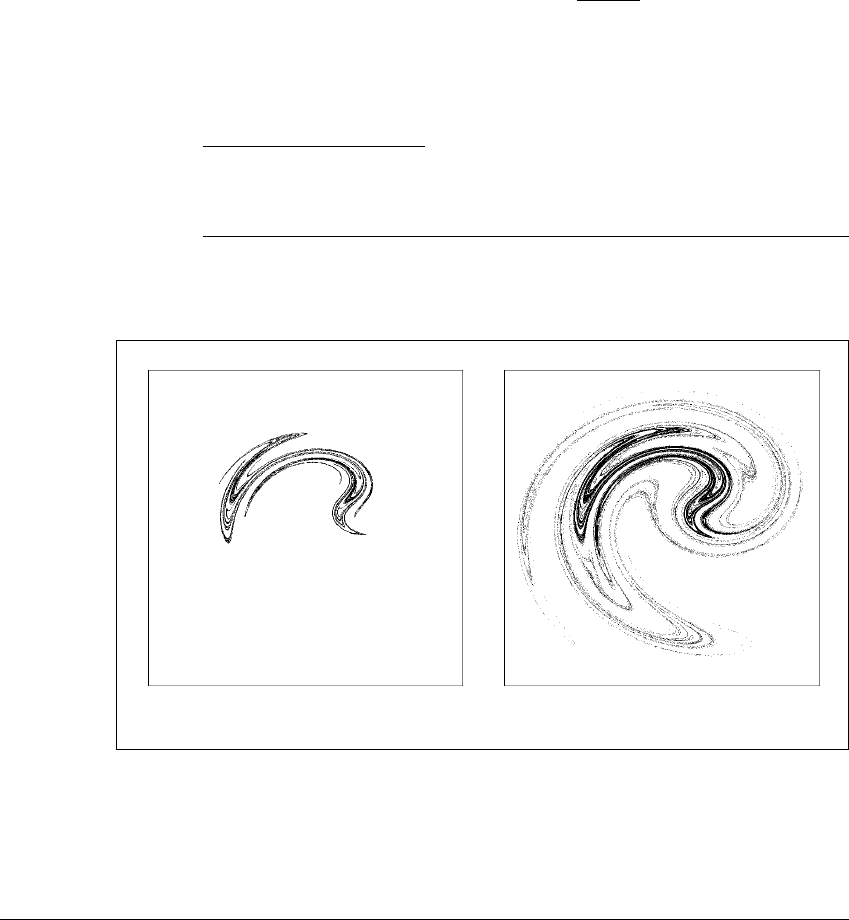
Using Theorem 10.9, we can interpret the crisis in the Ikeda example above.

Figure 10.16 shows that as a parameter a nears a crisis value a

, the attractor

␪

approaches the stable manifold of a period-ﬁve point p

. At a

, the outer edge of

␪

is tangent to this stable manifold; for every a ⬎ a

␪

has crossed the stable

manifold. See Figure 10.16. Once there is a crossing, the

␭

-Lemma tells us that

forward iterates of portions of

␪

limit on the entire unstable manifold of the

periodic point p

. Thus for each a ⬎ a

␪

contains both branches of U(p

). We

see a jump in the size of the attractor as

␪

ﬁlls out to U(p

). It is important that

U(p

) is contained in the basin of attraction of

␪

for a near a

. In this case we

say that there is an interior crisis at a ⫽ a

. Speciﬁcally, at an interior crisis, the

attractor jumps discontinuously in size. As a passes a

, the attractor collides with

a saddle ﬁxed point or periodic point p and suddenly incorporates the outward

branch of the unstable manifold of p.

416

10.3 CRISES

(a)

(b)

(c)

(d)

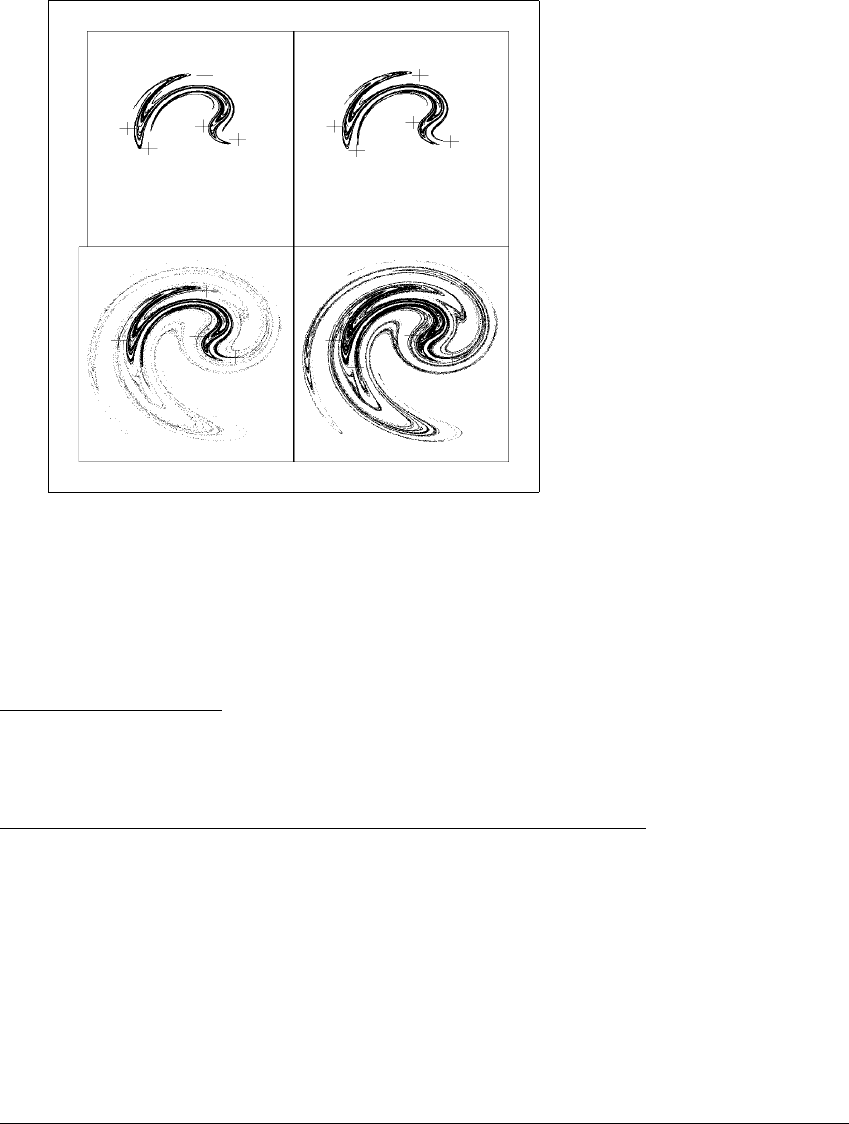
Figure 10.16 Crisis of the Ikeda attractor.

The numerically observed chaotic attractor of the Ikeda map is plotted for parameter

values (a) a ⫽ 7.1(b)a ⫽ 7.2(c)a ⫽ 7.25 (d) a ⫽ 7.3. One million points are

plotted in each part. The crisis parameter value occurs between (b) and (c). The

ﬁve crosses in each picture show the location of a period-ﬁve saddle with which the

attractor collides at the crisis. Another version of (c) appears in Color Plate 1.

✎ E XERCISE T10.4

Let p be a ﬁxed point or periodic point. Show that if a point v 僆 S(p)isa

limit point of an attractor

␪

, then p is also a limit point of

␪

Sometimes one branch of an unstable manifold is not in the basin of the

attractor

␪

for a ⬍ a

, but then crosses the basin boundary for a ⬎ a

and is drawn

into

␪

. Such is the case in the crises shown in Figure 10.17, in which the pieces

of a two-piece chaotic attractor are observed to merge. The result is an interior

crisis in which each piece (under the second iterate of the map) suddenly jumps

in size. Prior to the crisis, each branch of the unstable manifold of the boundary

saddle goes to a distinct piece of the attractor. After the crisis, both branches of

the unstable manifold are contained in the resulting one-piece attractor. Exercise

T10.5 refers to Figures 10.17 and 10.18.

417

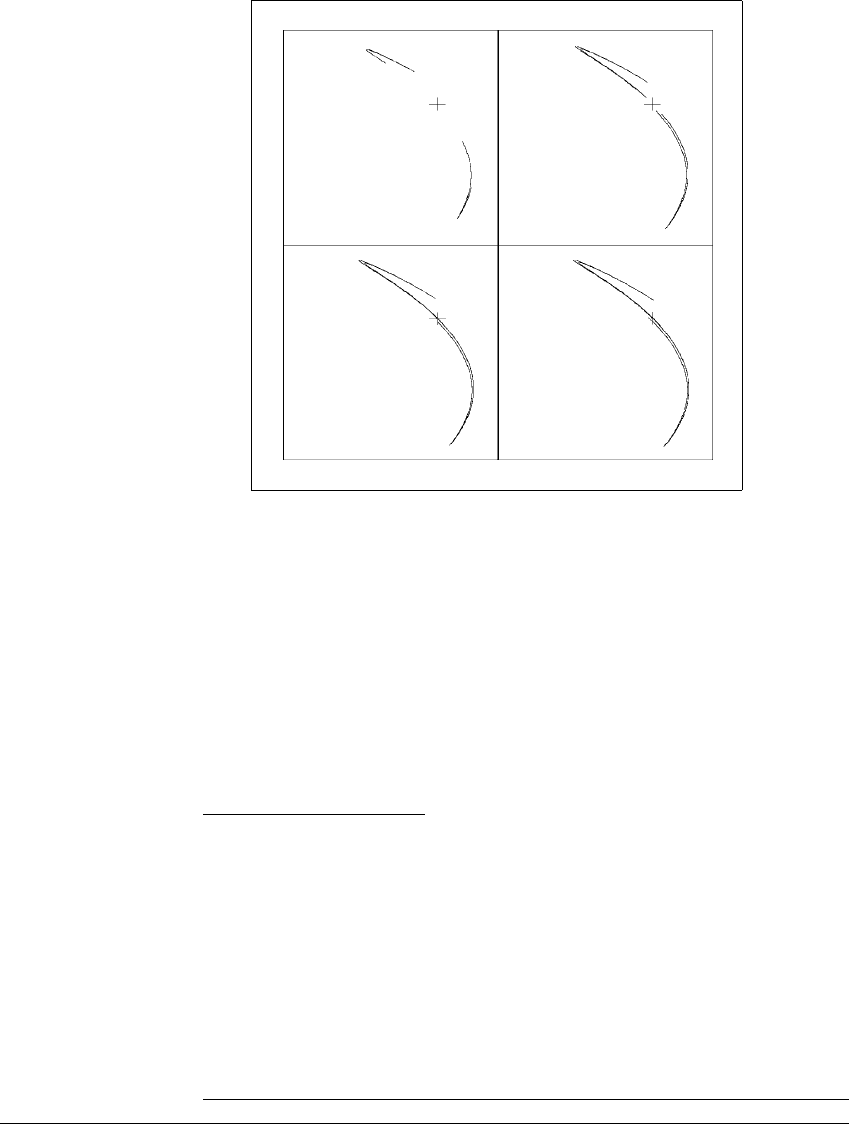
S TA B LE M ANIFOLDS AND C RISES

Figure 10.17 Crisis of a two-piece H

enon attractor.

Numerically observed chaotic attractors of the H

enon map are shown for parameter

values a ⫽ 2.00, 2.01, 2.02, 2.03. Each ﬁgure is created by plotting a single trajectory.

A ﬁxed point saddle is also plotted. The two pieces of the attractor join when the

pieces simultaneously collide with the saddle.

✎ E XERCISE T10.5

Figure 10.17 shows what is numerically observed to be a chaotic attractor

for the H

enon map f

(x, y) ⫽ (a ⫺ x

⫺ 0.3y, x), at parameter values a ⫽

2.00, 2.01, 2.02, and 2.03. The attractor has two pieces for a ⬍ a

⬇ 2. 018.

Then the two pieces merge into one at a ⫽ a

. Although the attractor

appears to change continuously, there is a crisis at a

at which point the

two pieces of the attractor collide with a ﬁxed point p ⬇ (.91,.91). Figure

10.18 shows the attractor together with p and

S(p). Describe the evolution

of the attractor as it passes through the crisis.

418