Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

10.4 PROOF OF THE S TA BLE M ANIFOLD T HEOREM

y = x

y = kx

y = -kx

y = -x

Figure 10.24 Cones containing the stable manifold.

The proof of Lemma 10.17 shows that for any k ⬎ 0 the local stable set enters the

cone determined by the lines y ⫽⫾kx.

Lemmas 10.13–10.16 show (among other properties) that S

is contained

within the cone determined by the lines y ⫽⫾x. See Figure 10.24. If we decrease

the magnitude of the slope of these lines, we can similarly show that there is a

(perhaps smaller) square B

such that S

lies in the cone determined by y ⫽⫾kx,

0 ⬍ k ⬍ 1. Thus

␾

(x)

→ 0, as x → 0. This is the idea behind the proof of Lemma

10.17.

Lemma 10.17

␾



(0) ⫽ 0.

Proof: Given k ⬎ 0, choose

␦

⬎ 0 (the width of the square B

)small

enough so that

⑀

⬍ (u ⫺ 1) 2

1 ⫹

. (Recall that

␦

and

⑀

are related as in

Lemma 10.11.) Let p ⫽ (x, y) be a point in B

but outside the y ⫽⫾kx cone. The

vertical position of f(p) can be approximated by Lemma 10.11, as follows:

|f(p)

| ⱖ u|y| ⫺

⑀



⫹ y

ⱖ u|y| ⫺

⑀

⫹ y

⫽ |y|



u ⫺

⑀

⫹ 1



⬎ |y|



u ⫺

(u ⫺ 1)



⫽ |y|



u ⫹ 1



⫽ |p



u ⫹ 1



429

S TA B LE M ANIFOLDS AND C RISES

Therefore, points outside the y ⫽⫾kx cone have y-coordinates that in-

crease by a factor of

u⫹1

⬎ 1 per iteration, and so eventually move out of the

␦

-box B

. By the deﬁnition of local stable set, S

is in the y ⫽⫾kx cone.

The deﬁnition of derivative of

␾

(x) at 0 is lim

x→0

␾

(x)

. Since this ratio is

bounded between ⫺k and k for x near 0, for arbitrarily small k ⬎ 0, the limit exists

and equals 0.

10.5 STABLE AND UNSTABLE MANIFOLDS

FOR

HIGHER DIMENSIONAL MAPS

The Stable Manifold Theorem which is proved in Section 10.4 is for saddles in

the plane. Actually, any hyperbolic periodic point has a stable and an unstable

manifold. Recall that a periodic point of period k is called hyperbolic if Df

the point has no eigenvalues with absolute value 1. The deﬁnitions of stable and

unstable manifolds for these points are identical to Deﬁnition 2.18 for saddles in

the plane.

Deﬁnition 10.18 Let f be a smooth one-to-one map on ⺢

, and let p be

a hyperbolic ﬁxed point or hyperbolic periodic point for f.Thestable manifold

of p, denoted

S(p), is the set of points x 僆⺢

such that |f

(x) ⫺ f

(p)| → 0 as

n →

⬁

.Theunstable manifold of p, denoted

U(p), is the set of points x such

that |f

⫺n

(x) ⫺ f

⫺n

(p)| → 0 as n →

⬁

The other two types of hyperbolic ﬁxed points for maps of the plane are

sinks and sources. For a ﬁxed point p in the plane, if both eigenvalues of Df(p)are

of absolute value less than one, then p is a sink, and the stable manifold contains

a two-dimensional

⑀

-neighborhood of p. In this case, the entire stable manifold

is a “two-dimensional manifold”. In general, a k-dimensional manifold in ⺢

(or

a k-manifold) is the image of a smooth, one-to-one function of ⺢

into ⺢

. Thus

a two-manifold is a smooth surface.

The unstable manifold of a sink p in ⺢

is only the point p itself (a 0-

dimensional manifold). In the case of a repeller in ⺢

, in which Df(p) has two

eigenvalues outside the unit circle, the stable manifold is only p itself, while the

unstable manifold is a two-manifold (which in this case is a two-dimensional

subset of the plane).

430

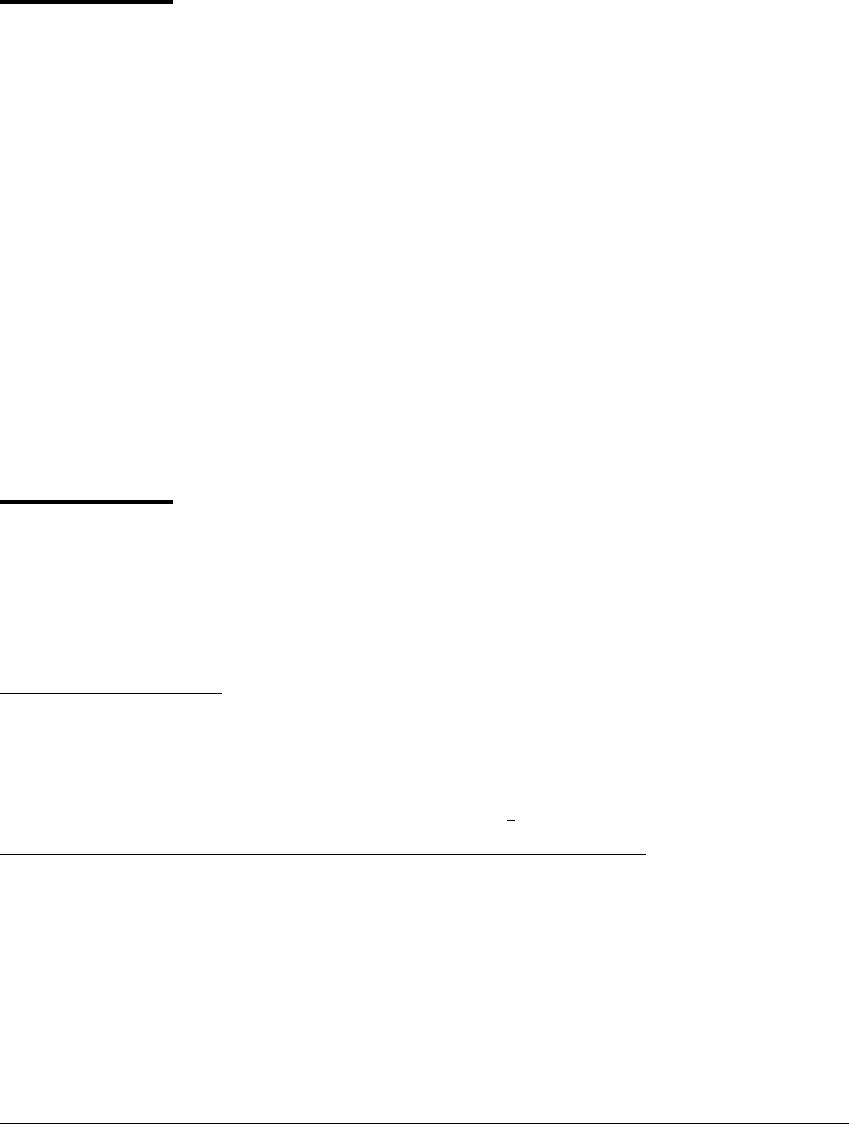
10.5 STA B L E A N D U NSTABLE M ANIFOLDS FOR H IGHER D IMENSIONAL M APS

E XAMPLE 10.19

Let f(x, y, z) ⫽ (⫺3x, .5y, ⫺.2z). Notice that f

(0,y,z) ⫽ (0, (.5)

(⫺.2)

z). Therefore, lim

k→

⬁

(0,y,z)| ⫽ 0, and the stable manifold of the

ﬁxed point (0, 0, 0) is seen to be the (y, z)-plane. The unstable manifold is the

x-axis, since f

⫺k

(x, 0, 0) ⫽ ((⫺3)

⫺k

(x), 0, 0).

There is a higher-dimensional version of Theorem 10.1. For a hyperbolic

ﬁxed point p of a higher-dimensional map, the stable manifold will have the same

dimension as the subspace of ⺢

on which the derivative contracts; that is, the

dimension is equal to the number of eigenvalues of Df(p) that have absolute value

strictly smaller than 1, counted with multiplicities. This subspace, the eigenspace

corresponding to these eigenvalues, will be tangent to the stable manifold at p.

Similarly, the unstable manifold has dimension equal to the number of eigenvalues

of Df(p) with absolute value strictly larger than 1, counted with multiplicities;

the linear subspace on which Df(p) expands is tangent to the unstable manifold

at p.

E XAMPLE 10.20

Let f(x, y, z) ⫽ (.5x, .5y, 2z ⫺ x

⫺ y

). The origin is the only ﬁxed point

of f, and its eigenvalues are 0.5, 0.5, and 2. The linear map Df(0) is contracting

on the (x, y)-plane and expanding on the z-axis. The (x, y)-plane, however, is

not the stable manifold for 0 under the nonlinear map f, as Exercise 10.6 shows.

✎ E XERCISE T10.6

Let f(x, y, z) ⫽ (.5x, .5y, 2z ⫺ x

⫺ y

(a) Show that

U(0)isthez-axis.

(b) Show that

S(0) is the paraboloid 兵(x, y, z):z ⫽

⫹ y

)其.

431

S TA B LE M ANIFOLDS AND C RISES

☞ C HALLENGE 10

The Lakes of Wada

ONSIDER THE TWO open half-planes L ⫽ 兵(x, y):x ⬍ 0其 and R ⫽ 兵(x, y):

x ⬎ 0其. Each of the two regions has a set of boundary points consisting of the

y-axis. Therefore, any boundary point of either of the two regions is a boundary

point of both regions. Can the same thing be done with three regions? It means

getting each boundary point of any one of the three regions to be a boundary

point of both of the others as well. A little thought should persuade you that such

sets will be a little out of the ordinary.

In 1910 the Dutch mathematician L.E.J. Brouwer gave a geometric con-

struction of three regions such that every boundary point is a boundary point of

all three regions. Independently, the Japanese mathematician Yoneyama (1917)

gave a similar example. Yoneyama attributed the example to “Mr. Wada”. This

example is described in (Hocking and Young, 1961); they called the example the

“Lakes of Wada”.

The ﬁrst three steps in the construction of this fractal are shown in Figure

10.25. Start with an island of diameter 1 mile. The ﬁrst lake is the exterior, white

region, and the other two are shaded gray and black. Now the excavation begins.

From the exterior region, dig a canal so that every point of land (the island) lies

Figure 10.25 Lakes of Wada.

432

C HALLENGE 10

no more than 1 2 mile from the white canal. Second, dig a gray canal so that no

land lies more than 1 3 mile from it. Third, dig a black canal so that no land lies

more than 1 4 mile from black water. Next, go back and extend the ﬁrst (white)

canal so that no land lies more than 1 5 mile from it (we have not shown this

step). Continue in this way. Of course, the three lakes must never intersect. Be

sure to pay the bulldozer operator by the amount of dirt moved and not by the

mileage traveled by the bulldozer. In the limit of this process, the area of the

remaining land is 0. Each shore point of any of the lakes is also a shore point for

both of the other lakes.

As originally presented, the Lakes of Wada have nothing to do with dy-

namical systems. Although we have seen basins of attraction with extremely

complicated, even fractal, boundaries, it is hard to imagine that such a conﬁgura-

tion of three basins could exist for any but the most contrived dynamical systems.

In this challenge, we present special trapping regions, called basin cells, whose

boundaries are formed by pieces of stable and unstable manifolds, to show that

“Wada basins” appear to exist in simple dynamical processes. We begin with a

few deﬁnitions of topological terms.

Let A be a subset of ⺢

. (Later concepts will pertain only to subsets of the

plane.) The boundary of A, denoted bd(A), is the set of points that have both

points in A and points not in A arbitrarily close to them. Speciﬁcally, x is in

bd(A) if and only if for every

⑀

⬎ 0, the neighborhood N

⑀

(x) contains points in

A and points not in A. Boundary points may be in A or not. For example, the

sets D

⫽ 兵x : |x|

ⱕ 1其 (the closed unit disk) and D

⫽ 兵x : |x|

⬍ 1其 (the open

unit disk) both have the same boundary; the unit circle C ⫽ 兵x : |x|

⫽ 1其. The

interior of A, denoted int(A), is the set of points in A that have neighborhoods

completely contained in A. Speciﬁcally, x is in int(A) if and only if there is an

⑀

⬎ 0suchthatN

⑀

is a subset of A. Notice that int(A)andbd(A) are disjoint

sets.

✎ E XERCISE T10.7

Show: int(D

) ⫽ D

AsetA is called open if it is equal to its interior. An open set does not

contain any boundary points. Assuming that A is an open set, we say a point y

in bd(A)isaccessible from A if there is a curve J such that y is an endpoint of

J, and all of J except y is in A. For our example of the disk, all points in bd(D

)

are accessible from D

. A somewhat more interesting example is shown in Figure

10.26. There the boundary of the open set U is shown to wind around two limit

433

S TA B LE M ANIFOLDS AND C RISES

Figure 10.26 The open set

winds around the circles inﬁnitely many times.

The point shown is accessible from U since it is the end of a curve contained in U.

Every point on the boundary of U is accessible except for those points on the limit

circles (the dashed circles).

circles. (The ﬁgure is intended to represent an inﬁnite number of windings of the

boundary around these limit circles.) All points on the boundary, except the limit

circles, are accessible from U. The circles, while in bd(U), contain no points

accessible from U.

Now we introduce dynamics to the situation. Let F be a one-to-one smooth

map of the plane. Recall that a trapping region is a bounded set Q, with int(Q)

not the empty set, with the property that F(Q) is a subset of Q and F(Q)isnot

equal to Q.Thebasin of a trapping region Q, denoted bas(Q), is the set of all

points whose trajectories enter int(Q). Those trajectories then remain in int(Q).

Step 1 Show that if Q is a trapping region, a trajectory that enters Q must

stay in Q for all future iterates. [Hint: If a set A is a subset of B,theF(A)isa

subset of F(B).]

Step 2 Prove two topological properties of basins:

(1) Show that bas(Q) is an open set. [Hint: Given x in bas(Q), let j be a

positive integer such that F

(x)isinint(Q). Use the continuity of F

to obtain

the result.]

(2) A set A is called path connected if, given any two points x and y in A,

there is a path contained in A with endpoints x and y. (Recall that a path is

a continuous function s :[0, 1] → ⺢

.) Show that if Q is path connected, then

bas(Q) is path connected.

434

C HALLENGE 10

(a) (b)

Figure 10.27 Basin cells.

In (a) a period-two orbit 兵p

其 “generates” the cell, while in (b) a period-three

orbit 兵q

其 generates the cell. Notice that basin cells cannot exist if there are

no homoclinic points.

The deﬁnition of basin cell is illustrated in Figure 10.27, where we see a

four-sided cell with a period-two point on the boundary and a six-sided cell with

a period-three point on its boundary. A cell is a region Q (homeomorphic to a

disk) whose boundary is piecewise smooth and consists of a ﬁnite number of pieces

of stable and unstable manifold of some orbit. Speciﬁcally, for a periodic orbit p

of period k, a cell is a planar region bounded by 2k sides: included among these

sides are pieces of both branches of the k stable manifolds as they emanate from

the k points in the orbit together with k pieces of unstable manifolds, one from

each of the k points in p. We denote by Q

the union of the points in p together

with points on the pieces of stable manifolds in the boundary of Q, and by Q

the union of points in pieces of unstable manifolds in the boundary that are not

already points of Q

. Then Q

and Q

are disjoint sets whose union is bd(Q).

In order to be able to verify whether a cell is a trapping region, the following

is useful and almost obvious, but is not easy to show:

If F(bd(Q)) is in Q,thenF(Q)isinQ.

Step 3 Show that a cell Q is a trapping region if and only if F(Q

)isa

subset of Q. Sketch an example of a cell that is not a trapping region.

A cell that is a trapping region is called a basin cell. From now on, we assume

that Q is a basin cell and investigate bas(Q) and its boundary. The concept of

basin cell was introduced and developed in (Nusse and Yorke, 1996).

435

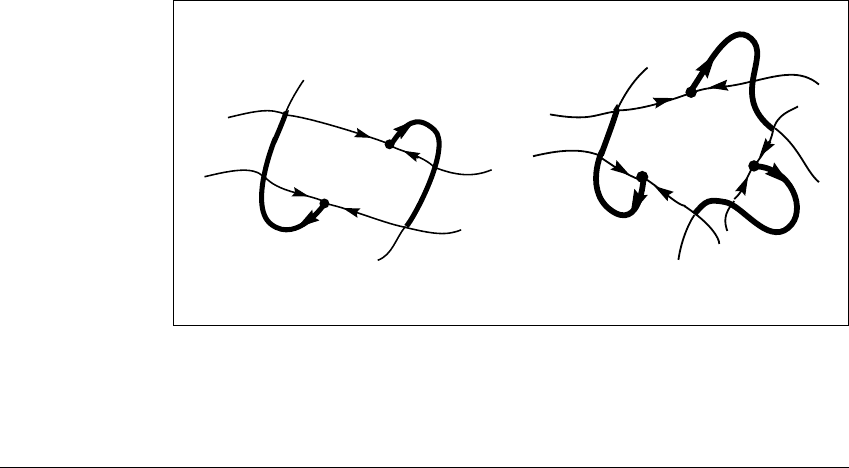
S TA B LE M ANIFOLDS AND C RISES

Proposition 1 describes the fundamental structure of basin boundaries.

When there are accessible periodic orbits, then all the accessible boundary points

are on stable manifolds. Although we prove the theorem only for basins with

basin cells, the result holds for a large class of planar diffeomorphisms. See, for

example, (Alligood and Yorke, 1992).

Proposition 1. Let Q be a basin cell and let x be in bd(bas(Q)). If x is accessible

from bas(Q), then x is on the stable manifold of p.

The proof of Proposition 1 is given in Steps 4, 5, and 6.

Step 4 Let x be in bd(bas(Q)) and denote F

(x)byx

. Show that x is

accessible from bas(Q) if and only if each x

,n⫽ 1, 2, 3,...,is accessible from

bas(Q). (The fact that bd(bas(Q)) is invariant under F should be included in the

proof.)

We can assume x is not a point of the orbit p, since such points are trivially

in the stable manifold of p. Let U be the union of the segments of unstable

manifold that are on bd(Q)(thesetQ

) together with the pieces of unstable

manifold that connect these segments to the orbit p. (See Figure 10.28.) We

assume further that x is not in U. (If it is, then for some positive integer n,the

point x

is not in U, and we can prove the result for x

(a) (b)

Figure 10.28 The sets

formed by pieces of unstable manifolds.

Segments of the unstable manifolds in the boundary of a cell, together with the

pieces of the manifolds needed to connect them to the periodic points make up the

set U.

436

C HALLENGE 10

Step 5 Since x is accessible from bas(Q), there is a curve J that is con-

tained in bas(Q) except for its endpoint which is x. Show that J can be chosen

so that it does not intersect U. Then prove that F

(J) does not intersect U, for

n ⫽ 0, 1, 2,....

Step 6 Let y denote a point in bas(Q)andinJ. We can choose n so that

(y) is in the interior of Q. (Why can we do this?) Show then that the entire

curve F

(J)isinQ for this n. Conclude that F

(x) is on the stable manifold of p.

Proposition 2. The accessible points are dense in the boundary of bas(Q).

Step 7 Prove Proposition 2. [Hint: On the straight line between a basin

point and a boundary point, there is an accessible (boundary) point.]

Proposition 3. If the unstable manifold of the orbit p that generates the cell Q

enters another basin B

, then every point in the boundary of bas(Q)isalsointhe

boundary of B

⫺0.4

⫺0.7

0.65 0.95

(a)

⫺1.5

01.5

(b)

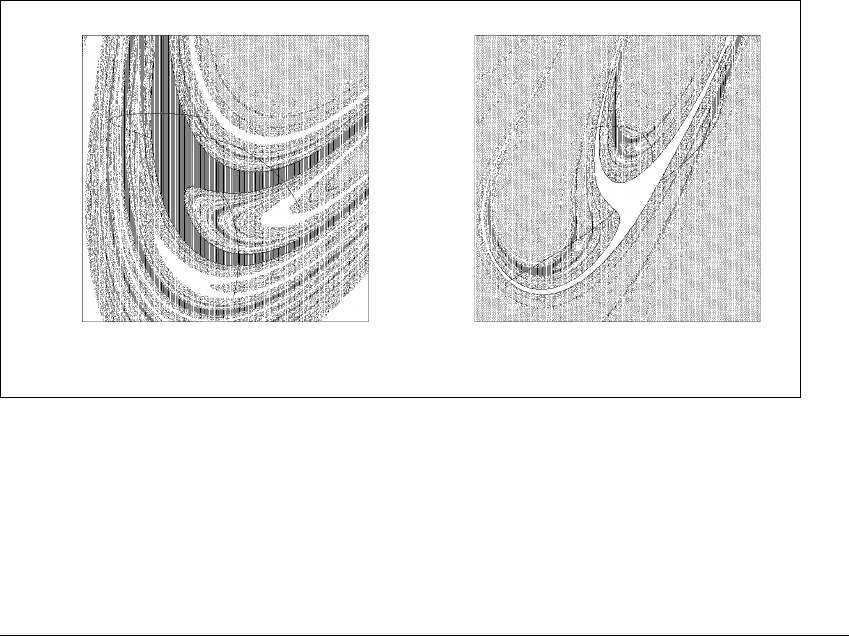
Figure 10.29 Basin cells for H

enon maps.

Parameters are set at a ⫽ 0.71 and b ⫽ 0.9. In (a) initial segments of unstable

manifolds emanating from a period-three accessible orbit are shown. The orbit is

accessible from the dark gray basin. The unstable manifolds intersect each of two

other basins, shown in light gray and white. Therefore, the gray basin is a Wada

basin. In (b) a similar conﬁguration is shown for the basin indicated in white. The

boundary of the white basin is also the boundary of the dark gray and the light gray

basins.

437

S TA B LE M ANIFOLDS AND C RISES

Figure 10.30 Three basin cells for the time-2

␲

map of the forced, damped

pendulum.

The white basin has one accessible periodic orbit of period two; the basin cell shown

has four sides. Similarly, the light gray basin has a four-sided basin cell. The dark

gray basin has one accessible periodic orbit of period three, producing a six-sided

cell.

Step 8 Prove Proposition 3. [Hint: First show, by the Lambda Lemma,

that the stable manifold of p is in the boundary of B

; then use Proposition 2 to

show that all of the boundary of bas(Q) is in the boundary of B

Finally, we say that a basin B is a Wada basin if there are two other basins

and B

such that every point in the boundary of B is also in the boundary of

and B

. We assume here that B, B

, and B

are pairwise disjoint. Wada basins

for H

enon maps are shown in Figure 10.29. The natural occurrence of the Lakes

of Wada phenomena in dynamical systems is described in (Kennedy and Yorke,

1991).

438