Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems
Подождите немного. Документ загружается.


B IFURCATIONS
We investigate the subject of generic bifurcations at greater length in Sec-
tion 11.4 and in Chapter 12. There we will see that the only “generic” bifurcations
are saddle-nodes and period-doubling bifurcations. Both Examples 11.4 and 11.5
contain nongeneric bifurcations. We can verify that they are atypical by showing
that the effect of adding a nonzero constant is to cause the map to revert to
a generic bifurcation. For example, add a constant b to the function g
a
to get
g
a
(x) ⫽ ax(1 ⫺ x) ⫹ b. It can be shown that for all b values but b ⫽ 0, the only
bifurcations of fixed points are saddle-node and period-doubling bifurcations.
Similarly, by adding a constant to the function f
a
in Example 11.5, obtaining
f
a
(x) ⫽ x
3
⫺ ax ⫹ b, we can say that fixed points come in through saddle nodes
for all b except 0. These facts are summarized in Exercise T11.3.
✎ E XERCISE T11.3
(a) Let g
a
(x) ⫽ ax(1 ⫺ x) ⫹ b. Show that when b ⫽ 0isfixedanda is
varied, the fixed points of g are born in saddle-node bifurcations.
(b) Let f
a
(x) ⫽ x
3
⫺ ax ⫹ b. Show that when b ⫽ 0, the fixed points
of f are born in saddle-node bifurcations.
11.3 CONTINUABILITY
In the bifurcation diagrams shown in Section 11.2, there are many intervals of
parameter values where the fixed or periodic points lie on a one-dimensional path
above the parameter axis. By a “path”, we mean a single-valued function of a.In
this case, there is one fixed point (or periodic point) for each value of a in an
interval. The paths are occasionally interrupted by bifurcation points.
For example, assume that f
a
is a family of one-dimensional maps, and assume
that x
a
is a fixed point of f
a
. In this section we will see that a path of fixed points
x
a
must continue as a is varied, without stopping or branching into two or more
paths, as long as f
a
(x
a
) does not equal 1. In the next section, we will see the
converse: that if f
a
(x
a
) crosses 1, then there must be extra fixed points in the
vicinity.
Definition 11.6 Let f
a
be a one-parameter family of maps on ⺢
n
. We
say a fixed point
v of f
a
is locally continuable, or simply continuable, if the fixed
points of f
a
for a near a lie on a continuous path (the graph of a continuous
function). More precisely, the set of fixed points of f in some neighborhood
460
11.3 CONTINUABILITY
(a ⫺ d, a ⫹ d) ⫻ N
⑀
(v) is the graph of a continuous function g from (a ⫺ d, a ⫹ d)
to N
⑀
(v):
兵(a, g(a)) : a 僆 (
a ⫺ d, a ⫹ d)其.
This definition is illustrated in Figure 11.13(b). A fixed point (a
c
, v
c
)onthepath
containing (
a, v) is called the continuation of (a, v)ata ⫽ a
c
.
We encountered examples of fixed points that are not locally continuable
in Section 11.1. The saddle-node bifurcation point (a, x) ⫽ (⫺1 4, ⫺1 2) of the
quadratic map f(a, x) ⫽ f
a
(x) ⫽ a ⫺ x
2
, shown in Figure 11.2, does not lie on a
path of fixed points which extends to values of a smaller than ⫺1 4, and thus does
not satisfy Definition 11.6. The map f has a period-doubling bifurcation at (
a, x) ⫽
(3 4, 1 2). As we shall see from Theorem 11.7, this point is locally continuable as
a fixed point of f because f
3 4
(
1
2
) ⫽⫺1. But it is not locally continuable as a fixed
point of f
2
, since the set of fixed points of f
2
in any neighborhood of (a, x) does
not form a one-dimensional path. Notice that the derivative of f
a
at the saddle
node x ⫽⫺1 2isf
⫺1 4
(⫺1 2) ⫽⫺2(⫺1 2) ⫽⫹1. The derivative of f
2
at the
period-doubling bifurcation is (f
2
3 4
)
(1 2) ⫽ f
3 4
(1 2)f
3 4
(1 2) ⫽ (⫺1)
2
⫽ 1.
x
xx + h - h
x - h
x + h
z
1
z
2
a
a
( a, x )
a
1
a
2
( a
1
, z
1
)
( a
2
, z
2
)
(a) (b)
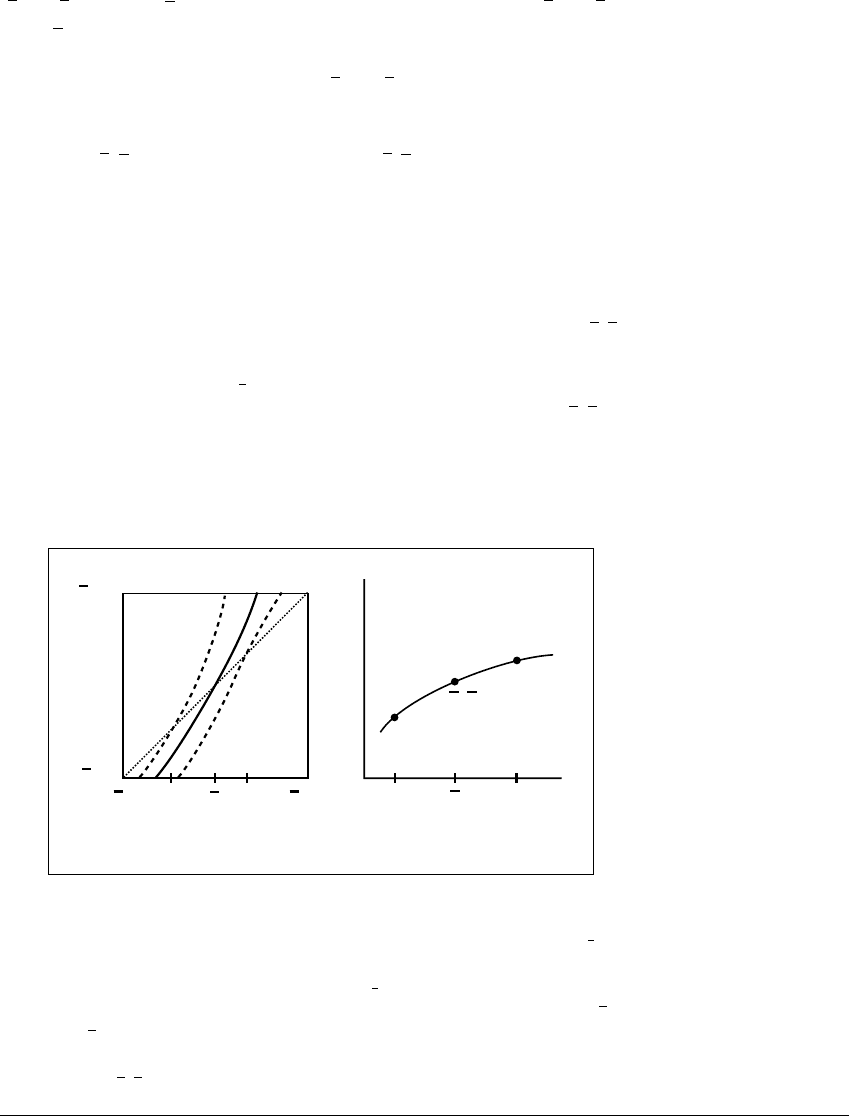
Figure 11.13 Graph of a scalar map
f
with a hyperbolic fixed point.
(a)Anintervalonwhichf
a
⬎ 1 is shown. For small perturbations of f
a
(small
changes in a) the graph and derivatives of points near the fixed point remain close
to those of the original map. The graph of f
a
is indicated with a solid curve. The
dashed curves are the graphs of maps f
a
1
and f
a
2
, where a
1
and a
2
are near a, and
a
1
⬍ a ⬍ a
2
. The map f
a
1
has one fixed point at z
1
, and the map f
a
2
has one fixed
point at z
2
. (b) The bifurcation diagram shows a continuous path of fixed points
through (
a, x).
461

B IFURCATIONS
When the derivative at a fixed point is not ⫹1, the fixed point is con-
tinuable. This is the content of Theorem 11.7. Assume for example that f
a
⬎ 1.
Then f
a
is below the diagonal to the left of x, above the diagonal to the right of
x, and the slope is strictly greater than one. If these three key facts are true for f
a
,
and if f
a
is continuous in the parameter a, then these three facts will also hold for
all f
a
where a ⫺ d ⬍ a ⬍ a ⫹ d, for some d ⬎ 0. The conclusion is that there is a
single fixed point for f
a
whenever a is near a; these fixed points together form a
continuous path in the parameter a.
We prove only part (a), the one-dimensional case, and illustrate part (b)
in Example 11.8 following the proof. Theorem 11.7 is really a special case of the
implicit function theorem. See, for example, (Fitzpatrick, 1996).
Theorem 11.7 (a) Let f be a smooth one-parameter family of maps defined
on a subset of ⺢.If
x is a fixed point of f
a
and if the derivative f
a
(x) is not ⫹1, then
(
a, x) is continuable.
(b) Let f be a smooth one-parameter family of maps defined on a subset of
⺢
n
,n ⬎ 1.Ifv is a fixed point of f
a
and if ⫹1 is not an eigenvalue of Df
a
(v), then
(
a, v) is continuable.
Proof of (a): Assume that f
a
(x) ⬎ 1. The case f
a
(x) ⬍ 1 is analogous.
The fixed point satisfies f
a
(x) ⫽ x. Because f is continuously differentiable in the
two variables a and x, the fact that f
a
(x) ⬎ 1 implies that f
a
(x) ⬎ 1 for a and x in
some square [
a ⫺ h, a ⫹ h] ⫻ [x ⫺ h, x ⫹ h], where h ⬎ 0. Furthermore, because f
is continuous in a and both
f
a
(x ⫺ h) ⫺ (x ⫺ h) ⬍ 0andf
a
(x ⫹ h) ⫺ (x ⫹ h) ⬎ 0,
we know that
f
a
(x ⫺ h) ⫺ (x ⫺ h) ⬍ 0andf
a
(x ⫹ h) ⫺ (x ⫹ h) ⬎ 0
for all a in a perhaps smaller interval of parameters [a ⫺ d, a ⫹ d], where d ⬎ 0.
Now we are in the situation of Figure 11.13(a). For all a in a small interval,
the function f
a
has slope greater than one over a small interval of x, and straddles
the diagonal. Thus for each a in the interval [
a ⫺ d, a ⫹ d] there is a unique fixed
point p
a
of f
a
in the interval [x ⫺ h, x ⫹ h].
Since the function f
a
changes continuously with the parameter a, the fixed
points p
a
form a continuous path in a. To see this, let a be any point in the interval
and let a
i
→ a be a sequence such that lim
i→
⬁
p
a
i
⫽ p
ⴱ
. Then the continuity of f
a
462
11.3 CONTINUABILITY
implies that
f
a
(p
ⴱ
) ⫽ lim
i→
⬁
f
a
i
(p
a
i
) ⫽ lim
i→
⬁
p
a
i
⫽ p
ⴱ
.
Therefore p
ⴱ
is the unique fixed point p
a
, and the path is continuous.
In the following example we investigate the set of fixed points of the
H
´
enon family of Example 11.3 via the Implicit Function Theorem. Not only is
this theorem the mathematical basis of Theorem 11.7(b), but it also shows us
that finding out whether an orbit has an eigenvalue of ⫹1 reduces to checking
the singularity of a 2 ⫻ 2 matrix.
E XAMPLE 11.8
Fix the parameter b and let h : ⺢
3
→ ⺢
2
be given by
h(a, x, y) ⫽ (a ⫺ x
2
⫹ by, x). (11.2)
Recall that the set of fixed points of h is the same as the set Z of zeroes of
the related function k(a, x, y) ⫽ (x, y) ⫺ h(a, x, y). As in the proof of Theorem
11.7, it turns out to be easier to deal with zeroes than with fixed points. Let
(
a, v) ⫽ (a, x, y)beazeroofk (fixed point of h). Now ⫹1 is not an eigenvalue of
Dh(
a, v) if and only if 0 is not an eigenvalue of Dk(a, v), if and only if Dk(a, v)
is nonsingular. Then the Implicit Function Theorem says that there is a three-
dimensional neighborhood V of (
a, v)suchthatZ 傽 V is a (one-dimensional)
path in a. In other words, (
a, v) is a continuable fixed point of k. This is just a
restatement of Theorem 11.7(b).
In order to investigate Jacobian matrices containing various combinations
of partial derivatives in this example, we write D
(a,x,y)
for the 2 ⫻ 3 matrix of
partial derivatives with respect to a, x, and y. The notations D
(x,y)
, D
(a,x)
, and
D
(a,y)
represent the Jacobian matrices of partial derivatives with respect to the
two variables indicated. For (
a, x, y)inZ,
D
(a,x,y)
k(a, x, y) ⫽
1 ⫺1 ⫺ 2
xb
01⫺1
.
Since D
(x,y)
k(a, x, y) is singular for 1 ⫹ 2x ⫽ b, there is a path that can be
parametrized by a through each point in Z except (
a, x, y) ⫽ (⫺
1
4
(1 ⫺ b)
2
, ⫺(1 ⫺
b) 2, ⫺(1 ⫺ b) 2), at which point there is a saddle node bifurcation. We can
solve for the solution (x, y) for a greater than ⫺
1
4
(1 ⫺ b)
2
; namely,
463
B IFURCATIONS
(x, y) ⫽
⫺(1 ⫺ b) ⫹
(1 ⫺ b)
2
⫹ 4a
2
,
⫺(1 ⫺ b) ⫹
(1 ⫺ b)
2
⫹ 4a
2
(11.3)
Sometimes you may want to consider a coordinate other than a as the
parameter. Since the 2 ⫻ 2 matrix D
(a,x)
is nonsingular for all values of (a, x, y),
the entire set of zeroes can be parametrized by y; namely,
(a, x) ⫽ (y
2
⫹ (1 ⫺ b)y, y) (11.4)
Also since D
(a,y)
is nonsingular everywhere, the entire set Z can be written as a
function of x.
11.4 BIFURCATIONS OF ONE-DIMENSIONAL
MAPS
We continue to investigate what can happen in a bifurcation diagram. We
have just seen that paths of fixed points must continue unless the derivative
passes through ⫹1. In this section, we investigate the converse question for one-
dimensional maps. If the derivative does pass through ⫹1 along a path of fixed
points, must there be a bifurcation? The answer is yes. Moreover, if the deriva-
tive passes through ⫺1, there must be a period-doubling bifurcation, since the
derivative of f
a
2
passes through ⫹1.
To begin, we describe conditions on specific partial derivatives which imply
the existence of a saddle-node bifurcation.
Theorem 11.9 (Saddle-node bifurcation.) Let f
a
be a smooth one-parameter
family of one-dimensional maps. Assume that
x is a fixed point of f
a
such that f
a
(x) ⫽ 1.
Assume further that
A ⫽
f
a
(
a, x) ⫽ 0 and D ⫽
2
f
x
2
(a, x) ⫽ 0.
Then two curves of fixed points emanate from (
a, x). The fixed points exist for a ⬎ a
if DA ⬍ 0 and for a ⬍
aifDA⬎ 0.
Proof: We will use Theorem 11.7, but with the roles of x and a reversed.
Consider the map g(a, x) ⫽ f(a, x) ⫹ a ⫺ x. Note that (1) g(a, x) ⫽ a if and only
if f(a, x) ⫽ x,(2)g(
a, x) ⫽ a and (3)
g
a(a, x) ⫽ A ⫹ 1 ⫽ 1 by hypothesis.
Theorem 11.7 implies that fixed points of a → g(a, x), and therefore the fixed
464
11.4 BIFURCATIONS OF O NE-DIMENSIONAL M APS
x
xx + h - h
x - h
x + h
z
1
z
2
a
( a, x )
a
1
a
2
( a
2
, z
2
)
( a
2
, z
1
)
(a) (b)
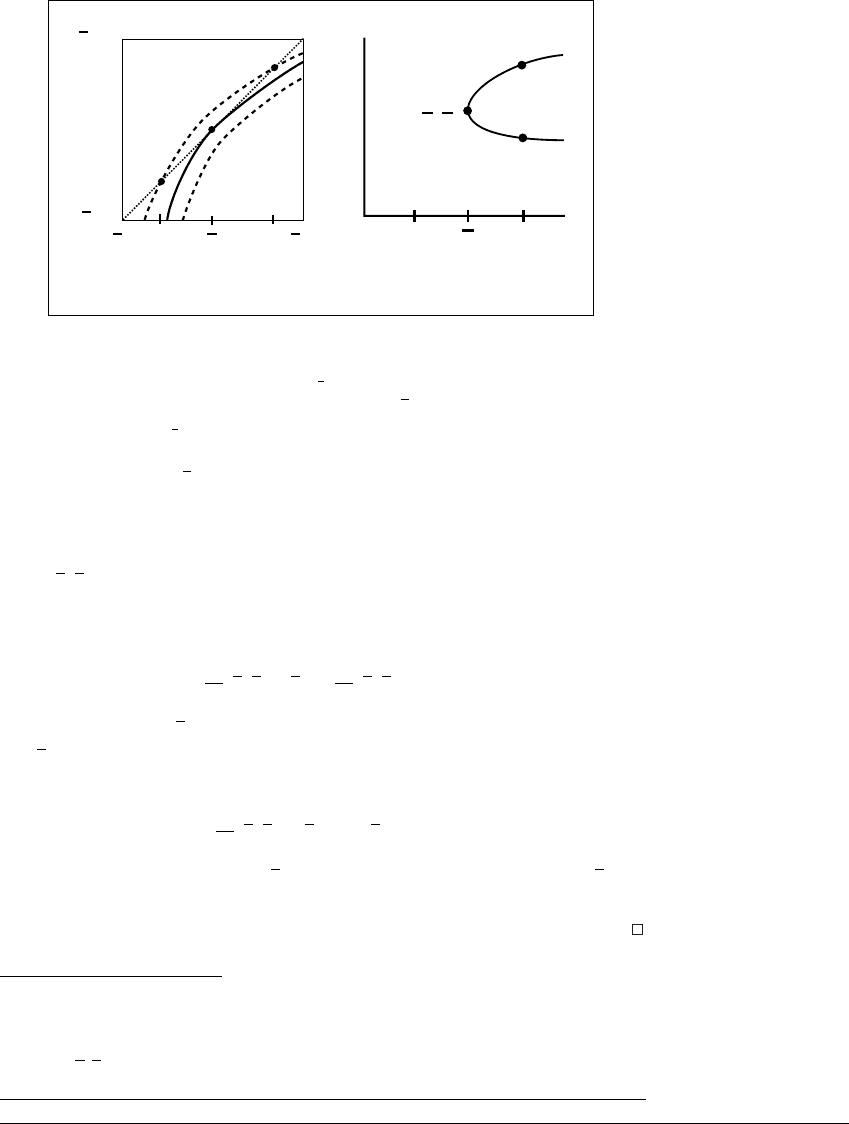
Figure 11.14 Graphs of a family of maps near a saddle-node bifurcation.
(a) The solid curve is the graph of f
a
, and the dashed curves show the graphs of
maps f
a
1
and f
a
2
for a
1
and a
2
near a, and a
1
⬍ a ⬍ a
2
. The map f
a
1
has no fixed
points, the map f
a
has one fixed point (the bifurcation point), and the map f
a
2
has
two fixed points, z
1
and z
2
. (b) In the bifurcation diagram, two paths of fixed points
are created at a ⫽
a.
points of x → f(a, x), can be continued in a path parametrized by x through the
point (
a, x). Such a path is shown in Figure 11.14(b).
We will call the path (p(x),x)in(a, x)-space. The fact that they are fixed
points of f
a
is written as f(p(x),x) ⫽ x. By the chain rule, we calculate
f
a
(
a, x)p
(x) ⫹
f
x
(
a, x) ⫽ 1, (11.5)
which implies that p
(x) ⫽ 0. Therefore the curve a ⫽ p(x) has a critical point at
x ⫽
x, also shown in Figure 11.14(b).
Taking one more derivative of (11.5) with respect to x yields
f
a
(
a, x)p
(x) ⫹ f
a
(x) ⫽ 0. (11.6)
Therefore DA ⬍ 0 means that p
(x) ⬎ 0, so that p(x) is concave up at x ⫽ x.The
path opens up to the right, as in Figure 11.14(b). If DA ⬎ 0, the path is reversed.
✎ E XERCISE T11.4
Show that the saddle-node bifurcation of fixed points for f (a, x) ⫽ a ⫺ x
2
at (a, x) ⫽ (⫺1 4, ⫺1 2) opens to the right as in Figure 11.14(b).
465

B IFURCATIONS
Theorem 11.10 Let f
a
be a smooth one-parameter family of one-dimensional
maps, and assume that there is a path of fixed points parametrized by a through (
a, x).If
f
a
(x) evaluated along the path crosses ⫹1 at (a, x), then every neighborhood of (a, x)
in ⺢ ⫻ ⺢ contains a fixed point not on the path.
Proof: For ease of exposition, we assume that the fixed points on the path
have x-coordinate 0. Otherwise, replace (a, x)by(a, u), where u ⫽ x ⫺ x(a).
Notice then that
df
du
(a, 0) ⫽
df
dx
(a, x(a)).
We argue the case in which f
a
(0) ⬎ 1 for a ⬍ a,andf
a
(0) ⬍ 1 for a ⬎ a.
(The proof in the other case is analogous.) Then, as shown in Figure 11.15, there
is an h ⬎ 0suchthat
f
a⫺h
(h) ⫺ h ⬎ 0andf
a⫹h
(h) ⫺ h ⬍ 0,
and also
f
a⫺h
(⫺h) ⫺ (⫺h) ⬍ 0andf
a⫹h
(⫺h) ⫺ (⫺h) ⬎ 0.
Since f
a
(x) is continuous in a, there exist a
1
and a
2
in the interval [a ⫺ h, a ⫹ h]
satisfying f
a
1
(h) ⫽ h and f
a
2
(⫺h) ⫽⫺h.Sinceh can be chosen as small as desired
0 h
- h
- h
0
h
a
( a, x )
a
1
a
2
(a
1
, h)
(a
2
, - h)
(a) (b)
Figure 11.15 A family of maps where the derivative crosses 1.
(a) The dashed curves denote f
a⫺h
and f
a⫹h
in Theorem 11.10. The open circles
straddle the diagonal, implying that f
a
has fixed points other than 0 for parameter a
between
a ⫺ h and a ⫹ h. (b) In the bifurcation diagram, a continuous path of fixed
points bifurcates into paths of new fixed points. This is one of several possibilities
when the derivative along a path of fixed points crosses 1.
466
11.4 BIFURCATIONS OF O NE-DIMENSIONAL M APS
but is nonzero, there are fixed points of f
a
as near to (a, x) as needed. In fact, our
argument shows that there are fixed points above and below the path.
A word of caution: It is possible that the new fixed points in the conclusion
of Theorem 11.10 exist for the single parameter value a ⫽
a. For example, the
family f
a
(x) ⫽ ax satisfies the hypotheses for the bifurcation value a ⫽ 1. It is true
that every neighborhood of (
a, x) ⫽ (1, 0) has fixed points other than 0, all of
them occurring at
a ⫽ 1 because every point is a fixed point for f
1
(x).
The transcritical bifurcation diagram of Figure 11.10 is an illustration of
Theorem 11.10. For example, pick either of the paths in Figure 11.10 and follow
it toward the bifurcation point. The map is f
a
(x) ⫽ ax(1 ⫺ x)andsof
a
(x) ⫽
a(1 ⫺ 2x). On the path of fixed points x ⫽ 0, the derivative f
a
(0) ⫽ 1 is reached
at parameter value a ⫽ 1. In every neighborhood of this point there are points
from the other path of fixed points. The pitchfork bifurcation of Figure 11.12 is
another illustration of Theorem 11.10.
Theorem 11.11 Let f be a smooth one-parameter family of maps. Assume
that
x is a fixed point of f
a
such that f
a
(x) ⫽⫺1.Iff
a
(x) evaluated along the path of
fixed points through (
a, x) crosses ⫺1 at (a, x), then every neighborhood of (a, x) (in
⺢ ⫻ ⺢ ) contains a period-two orbit.
Proof: Define g
a
⫽ f
2
a
and apply Theorem 11.10. The chain rule shows
that the derivative of g
a
passes through 1 at a ⫽ a. Therefore g
a
has fixed points
other than the fixed point of f
a
in any neighborhood of (a, x). Since f
a
(x) ⫽⫺1,
the fixed point
x is continuable, so the others must be period-two points of f
a
.
Table 11.1 summarizes information about the bifurcations we have de-
scribed. If we follow a path of fixed points of a one-dimensional map, bifurcations
can occur when the derivative becomes 1 or ⫺1. Saddle-node and period-doubling
Bifurcation
f
x
(
a,x
)
f
a
(
a,x
)
saddle node 1 ⫽ 0
pitchfork, transcritical 1 0
period-doubling ⫺1 ⫽ 0
Table 11.1 Identification of common bifurcations in one-dimensional maps.
When the derivative at the fixed point is 1 or ⫺1, the type of bifurcation depends
on other partial derivatives.
467

B IFURCATIONS
bifurcations are the “generic”, or commonly expected bifurcations, according
to the table, because they don’t depend on anything special happening at the
bifurcation point. A pitchfork bifurcation can only happen if the bifurcation
point (
a, x) coincides with a point where
f
a(a, x) ⫽ 0, a low probability event.
However, certain special conditions that are forced on the family by symmetry
and other reasons, can cause pitchfork bifurcations to occur, as in Example 11.5.
✎ E XERCISE T11.5
Let f
a
be a family of one-dimensional maps, and assume that (a, x)isafixed
point that is either a pitchfork bifurcation point or a transcritical bifurcation
point. Then the set Z of fixed points of f
a
cannot be expressed as a (single-
valued) function either of a or of x in any neighborhood of (
a, x). We have
seen that since Z is not locally continuable as a path in a, the derivative
f
a
(a, x) ⫽
f
x(a, x)mustbe⫹1. Show that, in addition, since Z is not
locally continuable as a path in x, the derivative
f
a(a, x)is0.
There is no end to the variety of behavior that can be seen in nongeneric
bifurcations. As a mild indication, in Exercise T11.6, four fixed points are created
at the bifurcation point.
✎ E XERCISE T11.6
Let f
a
(x) ⫽ x
4
⫺ 3ax
2
⫹ x ⫹ 2a
2
.Sketchthegraphoff
a
for a ⬍ 0anda ⬎ 0
and conclude that (
a, x) ⫽ (0, 0) is a bifurcation point. Find the four fixed
points of f
a
for a ⬎ 0. Calculate the partial derivatives of Table 11.1 to
determine in which ways this bifurcation fails to be generic.
11.5 BIFURCATIONS IN PLANE MAPS:
A
REA-CONTRACTING CASE
Many of the ideas we presented in Section 11.4 of this chapter carry over to
the study of bifurcations in one-parameter families of two-dimensional maps.
To illustrate this idea, we look at a simple extension of the logistic family to
468

11.5 BIFURCATIONS IN P LANE M APS:AREA-CONTRACTING C ASE
two-dimensions:
f
a
(x, y) ⫽ (g
a
(x), 0.2y),
where g
a
(x) ⫽ ax(1 ⫺ x). The Jacobian D
v
f
a
(x, y) has eigenvalues e
1
⫽ g
a
(x)and
e
2
⫽ 0.2. Again, the notation D
v
f
a
, which we will sometimes simplify to Df
a
,
denotes the matrix of partial derivatives with respect to the coordinates x and y
(the coordinates of the v vector), not a.
The version of Theorem 11.7 for one-parameter families of two-dimensional
maps says that a bifurcation of fixed points can only occur when ⫹1 is an eigen-
value of Df
a
. For f
a
this means that such bifurcations can only occur when g
a
is
⫹1. Of course, because of the special form of the map, bifurcations of f
a
occur
at precisely those parameter values at which g
a
has bifurcations. The hyperbolic
fixed points of f
a
are different than in the one-dimensional case: f
a
has only at-
tractors and saddles, whereas g
a
has only attractors and sources. At a saddle-node
bifurcation of f
a
one branch of attractors and one branch of saddles emanate from
the bifurcation orbit. At a period-doubling bifurcation, the eigenvalue e
1
goes
through ⫺1. A branch of fixed-point attractors changes to a branch of saddles as
two branches of period-two attractors (one branch for each point of the orbit)
bifurcate. These are the bifurcations pictured in Figure 11.8.
✎ E XERCISE T11.7
Let h
a
(x, y) ⫽ (g
a
(x), 3y). Classify the types of hyperbolic fixed points and
periodic orbits of h
a
. Which hyperbolic orbits make up the branches ema-
nating from saddle-node and period-doubling bifurcations?
Again, as in the one-dimensional case, we think of a periodic orbit as
one entity. Recall (from Chapter 2) that for a period-k orbit the eigenvalues of
Df
k
⫽ D(f
k
) are the same when the Jacobian is evaluated at any of the k points
in the orbit.
✎ E XERCISE T11.8
(a) Let A ⫽
m
11
m
12
m
21
m
22
. Show that the eigenvalues e
1
and e
2
are
continuous functions of the variables m
11
,m
12
,m
21
,m
22
. (b) Let f be a
smooth map of ⺢
2
. Show that the eigenvalues of Df
k
a
(v) depend continu-
ously on (a, v).
469
