Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

B IFURCATIONS

Describing saddle-node and period-doubling bifurcations for arbitrary fam-

ilies of two-dimensional maps is complicated by the fact that ﬁxed and periodic

points can have both contracting and expanding directions. Although the pre-

vious example is clearly a special case, the property of having one eigenvalue

with absolute value smaller than 1 at all points (or, analogously, one eigenvalue

with absolute value greater than 1 at all points) is one that holds for a large and

important class of maps. For such maps, the types of bifurcations that can occur

are limited to those seen in one-dimensional maps.

Deﬁnition 11.12 Let f be a smooth map of ⺢

, and let Df(v)bethe

Jacobian matrix of partial derivatives of f with respect to the v coordinates

evaluated at a point v 僆⺢

. We say f is area-contracting if | det Df(v)| ⬍ 1 for

all v 僆⺢

. The map f is area-preserving if | det Df(v)| ⫽ 1 for all v 僆⺢

It is a fact from advanced calculus that the number | det Df(v)| determines

thechangeinareaeffectedbythemapf near the point v.Infact,ifS is a region

in ⺢

,then

Area(f(S)) ⫽



| det Df(v)|dv.

See (Fitzpatrick, 1995).

Area-contracting maps represent an important class of dynamical systems.

Included in this class are time-T maps of dissipative systems of differential equa-

tions. An example is the time-2

␲

map of the forced, damped pendulum with

equation of motion

x ⫹ c

x ⫹ sin x ⫽ b cos t. We saw in Example 9.5 that with

damping c ⬎ 0, the Jacobian determinant is e

⫺2

␲

⬍ 1 for each x and

✎ E XERCISE T11.9

For which values of a and b is the H

enon map f(x, y) ⫽ (a ⫺ x

⫹ by, x)

area-contracting?

Let p be a periodic orbit of period k. We use the phrase “eigenvalues of p”to

refer to the eigenvalues of D

(p). For maps of the plane, D

(p) has eigenvalues

and e

. The area-contracting hypothesis implies |e

| ⬍ 1. In particular, at

least one of 兵e

其 must be inside the unit circle in the complex plane. The

unit circle is the set of complex numbers u ⫹ iv with modulus u

⫹ v

⫽ 1.

Thus the area-contracting hypothesis restricts the types of periodic orbits that

can occur. There are only two types of hyperbolic orbits: attractors or sinks (both

eigenvalues inside the unit circle) and saddles (one eigenvalue greater than ⫹1or

470

11.6 BIFURCATIONS IN P LANE M APS:AREA-PRESERVING C ASE

smaller than ⫺1). In Chapter 12, we need to distinguish between regular saddles

(one eigenvalue greater than ⫹1) and ﬂip saddles (one eigenvalue less than ⫺1).

Notice that the unstable orbits are all saddles, regular or ﬂip. There are no repellers

for area-contracting maps.

Similarly, the types of nonhyperbolic orbits are restricted by the area-

contracting hypothesis. There are only two types: orbits with one eigenvalue equal

to ⫹1, and orbits with one eigenvalue equal to ⫺1. As in the one-dimensional

case, the most frequently seen bifurcations are saddle-nodes and period-doublings.

The difference in the two-dimensional area-contracting case is that what were

paths of repellers in the one-dimensional case are replaced by paths of saddles,

ﬂip or regular, here. We discuss why the saddle-node and period-doubling bifur-

cations are those typically seen for families of one-dimensional maps and families

of area-contracting maps of the plane in Chapter 12.

➮ COMPUTER EXPERIMENT 11.1

Plot the period-6

␲

attracting orbit of the driven double-well Dufﬁng oscil-

lator

x ⫹ 0.1

x ⫺ x ⫹ x

⫽

␳

sin t for

␳

⫽ 5.9. Next, increase

␳

and locate the two

period-doubling bifurcations that occur for 5.9 ⬍

␳

⬍ 6.

11.6 BIFURCATIONS IN PLANE MAPS:

REA-PRESERVING CASE

In previous sections we saw that bifurcations of ﬁxed points or periodic points can

occur only at parameter values for which the derivative or an eigenvalue of the

orbit has absolute value one. For one-dimensional families, saddle nodes or period-

doubling bifurcations can occur when the derivative is 1 or ⫺1, respectively. For

families of maps of two or more (real) variables, there can be eigenvalues of

absolute value (magnitude) 1 which are not real numbers.

✎ E XERCISE T11.10

Let f be a map of ⺢

, and let p be a ﬁxed point of f.

(a) Show that if a ⫹ bi is an eigenvalue of Df(p), then the complex

conjugate a ⫺ bi is also an eigenvalue.

471

B IFURCATIONS

(b) Show that a bifurcation of a period-k orbit from a ﬁxed point can

only occur at a bifurcation orbit that has an eigenvalue that is a kth root of

unity.

In fact, a bifurcation of period-k orbits from a ﬁxed point can only occur

when a primitive kth root of unity is an eigenvalue. In families of one-dimensional

maps this means k ⫽ 1ork ⫽ 2. Bifurcations of higher-period orbits are similarly

ruled out for families of area-contracting maps of the plane. If, however, we

drop the area-contracting hypothesis, then bifurcations of higher-period orbits

(k ⬎ 2) can occur for families of two-dimensional maps. Unless there are special

symmetries or restrictions on the Jacobian (as in the case of area-preserving maps),

such bifurcations are rare compared to saddle nodes or period doublings. As we

discuss in Chapter 12, the latter two bifurcations are “generic”, in the sense that

most one-parameter families possess only these bifurcations.

To investigate how and when bifurcations of higher periods occur, we begin

with a family of two-dimensional linear maps.

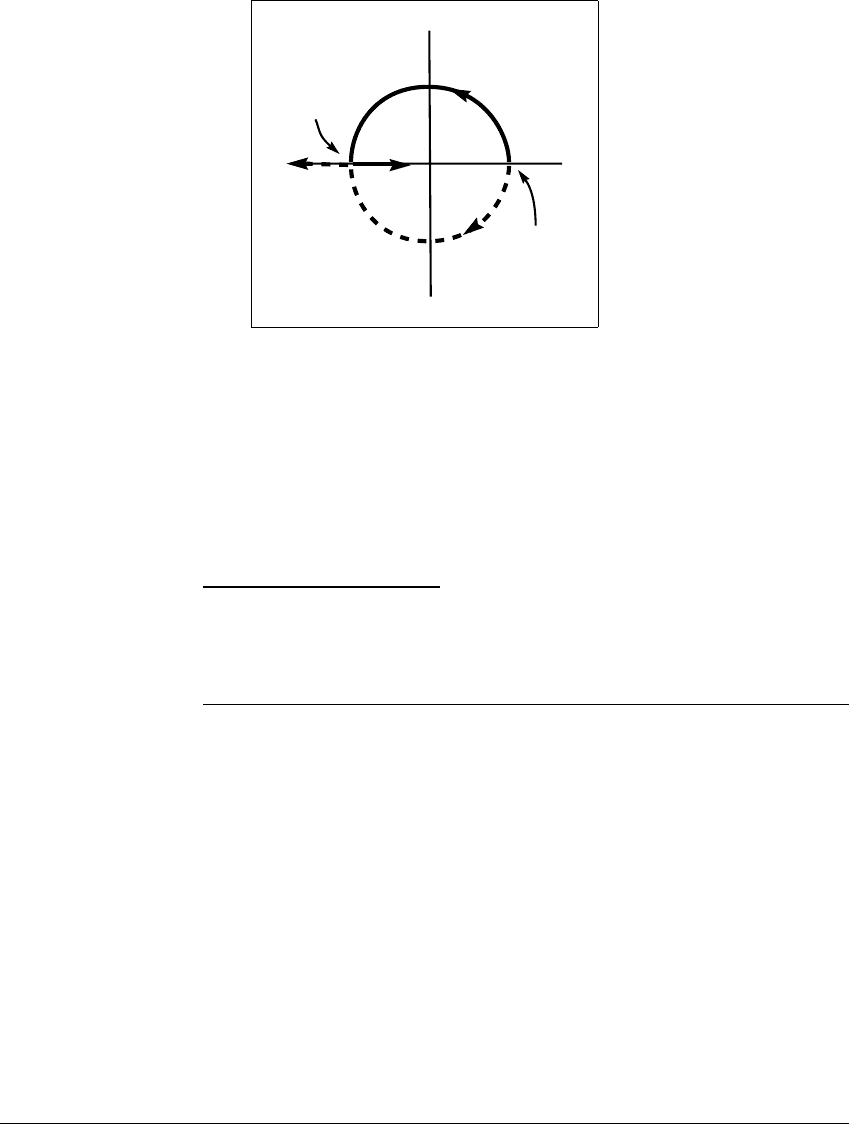
E XAMPLE 11.13

Let f

(x, y) ⫽ (

x ⫺



x ⫹

y), for a ⬎ 0, and x, y in ⺢. When

a ⫽ 1, the map rotates all nonzero vectors through an angle of

␲

 3. The origin is

ﬁxed. When the eigenvalues of a ﬁxed point all lie on the unit circle, it is called an

elliptic ﬁxed point. The origin is elliptic for a ⫽ 1. Although an elliptic ﬁxed point

of a linear map is not attracting, it is stable, meaning that for each neighborhood

␧

, there is a (perhaps smaller) neighborhood N

␦

such that all orbits beginning

in N

␦

remain in N

␧

. Orbits that start close stay close. For nonlinear maps, elliptic

ﬁxed points may or may not be stable.

It is worthwhile here to think of a “path” e(a) of eigenvalues (parametrized

by a); speciﬁcally, e(a) ⫽ a(

⫹ i



), which for 0 ⬍ a ⬍ 1 begins inside the unit

circle and crosses the unit circle when a ⫽ 1 at a sixth root of unity. Another

path of eigenvalues consists of the complex conjugate of e(a), for each a ⬎ 0. For

0 ⬍ a ⬍ 1, the origin is a sink; for a ⬎ 1, the origin is a source; and at a ⫽ 1,

the origin is an elliptic point around which all other points rotate on invariant

circles through an angle of

␲

 3. In the last case, all other points are period-six

points.

For a one-parameter family f

of nonlinear planar maps, we know that the

eigenvalues of Df

are the key to detecting changes of stability that might result

in bifurcations. To locate bifurcations of period-k orbits along a path of ﬁxed

472

11.6 BIFURCATIONS IN P LANE M APS:AREA-PRESERVING C ASE

points, we look for points at which a path e(a) of eigenvalues crosses the unit

circle at a kth root of unity. If the path crosses the unit circle with nonzero speed

(if the derivative de da is nonzero), then a family of invariant closed curves will

bifurcate from the path of ﬁxed points. The family of closed curves may all occur

at one parameter value, such as the invariant circles in the previous linear case, or

they may occur in a path that emanates from the bifurcation parameter through

either smaller or larger parameter values. We do not discuss the dynamics that

occur on the invariant closed curves except to say that near the bifurcation point,

on each closed curve, points rotate near the rate given by the Jacobian at the

bifurcation orbit.

In Example 11.14, we investigate a bifurcation in the H

enon family which

produces a family of invariant closed curves as we pass from area-contracting to

area-expanding maps.

E XAMPLE 11.14

Let h

(x, y) ⫽ (⫺.75 ⫺ x

⫹ by, x). Recall that ⫺b is the Jacobian deter-

minant: h is area-contracting or area-expanding according to whether |b| is less

than or greater than 1. For b ⫽⫺1, there is a ﬁxed point at (⫺1 2, ⫺1 2) with

eigenvalues e ⫽

⫾



i, (two sixth-roots of unity). Figure 11.16 shows a neigh-

borhood of this ﬁxed point (or its continuation) as b varies from ⫺.9to⫺1.1.

The ﬁxed point goes from sink (Figure 11.16(a)) to source (Figure 11.16(b)). In

particular, Figure 11.16(c) shows invariant curves encircling the ﬁxed point at

b ⫽⫺1. Notice that the crossing stable and unstable manifolds of a nearby ﬁxed

point saddle form the boundary of the “elliptic” behavior at the original ﬁxed

point. There are no invariant closed curves for |b| ⫽ 1. (See Exercise T11.11

below.)

✎ E XERCISE T11.11

Show that an invertible map of ⺢

which is either area-contracting or

area-expanding can have no invariant closed curves (except points).

Families of area-preserving planar maps (see Defn. 11.12) can possess an

extremely rich bifurcation structure. We still see periodic saddle orbits in these

maps, but no sinks or sources. The stable orbits must be elliptic: Both eigenvalues

are on the unit circle.

473

B IFURCATIONS

(a) (b)

(c)

Figure 11.16 The continuation of two ﬁxed points in the H

enon family.

Various orbits of the map h

(x, y) ⫽ (⫺.75 ⫺ x

⫹ by, x) are shown for (x, y)in

[⫺2.5, 5.0] ⫻ [⫺2.5, 5.0]. (a) At b ⫽⫺0.9, the map is area-contracting and there

is an attracting ﬁxed point. The stable and unstable manifolds of a nearby saddle

ﬁxed point are depicted. One branch of the unstable manifold spirals into the

attractor. (b) At b ⫽⫺1.1, the map is area-expanding and there is a repelling ﬁxed

point (the continuation of the elliptic point at this parameter). Now the stable

manifold of the saddle is shown to spiral out of the repeller. (c) At the in-between

value b ⫽⫺1.0, the map is area-preserving and there is an elliptic ﬁxed point (the

continuation of the attractor at this parameter). The stable and unstable manifolds

of the saddle now cross in inﬁnitely many homoclinic points.

474

11.6 BIFURCATIONS IN P LANE M APS:AREA-PRESERVING C ASE

✎ E XERCISE T11.12

Show that there are no hyperbolic periodic or ﬁxed sinks or sources for

area-preserving maps of the plane.

We investigate the H

enon family again—this time ﬁxing b at ⫺1and

varying a. Each map in the resulting family is an area-preserving map.

E XAMPLE 11.15

Let h

(x, y) ⫽ (a ⫺ x

⫺ y, x). Verify that for each a, the plane map h

area-preserving. For a ⬍⫺1 there are no ﬁxed points. When a ⫽⫺1, a ﬁxed point

appears at (⫺1, ⫺1). This orbit has a double eigenvalue of ⫹1. For a ⬎⫺1, there

are two ﬁxed points: one that is unstable (a saddle) and one that begins as a stable

elliptic orbit for a near ⫺1. We follow the orbits along the second, stable path.

As a increases slightly beyond ⫺1, eigenvalues of these orbits are constrained

to the unit circle in the complex plane. Since for any ﬁxed parameter the two

eigenvalues must be complex conjugates, the two paths of eigenvalues move (with

increasing a) around the unit circle. One moves along the top (imaginary part

positive), and the other moves along the bottom (imaginary part negative) as

shown in Figure 11.17. When a ⫽ 3, the two paths of eigenvalues join at ⫺1,

where there is a period-doubling bifurcation. What type of behavior do you expect

near the elliptic ﬁxed point as a increases from ⫺1to3?

Our ﬁnal example of this section is called the standard map. Like the

enon family, it has been studied extensively as a prototype—in this case,

as a model for understanding nonlinear phenomena in area-preserving maps.

While Poincar

e maps for dissipative systems of differential equations are area-

contracting, Poincar

e maps for conservative systems are area-preserving.

E XAMPLE 11.16

(Standard map.) Let

(x, y) ⫽ (x ⫹ y(mod2

␲

),y⫹ a sin(x ⫹ y)(mod2

␲

)), (11.7)

for x 僆 [⫺

␲

], y 僆 [⫺

␲

]. Notice that the standard map S

is periodic with

period 2

␲

in both variables. That is, S

(x ⫹ 2

␲

,y) ⫽ S

(x, y)andS

(x, y ⫹ 2

␲

) ⫽

(x, y). Therefore, like the cat map of Challenge 2, only the values of x and y

modulo 2

␲

are important, and we can consider the phase space to be a torus.

475

B IFURCATIONS

a = 3

a = -1

Figure 11.17 Complex eigenvalues for a family of elliptic ﬁxed points.

Paths of eigenvalues in the complex plane for the continuation of an elliptic ﬁxed

point of the area-preserving H

enon family h(a, x, y) ⫽ (a ⫺ x

⫺ y, x) are depicted

schematically. The elliptic point is born at a ⫽⫺1, at which point both eigenvalues

are ⫹1. Then the paths split and move around the unit circle as complex conjugates.

The paths join at a period-doubling bifurcation when a ⫽ 3. There the ﬁxed point

loses stability, becoming a saddle, as one path of eigenvalues moves outside the unit

circle.

✎ E XERCISE T11.13

Let S

denote the standard map. Show that det(DS

(x, y)) ⫽ 1. Therefore,

is a one-parameter family of area-preserving maps.

When the parameter a is zero, the torus is ﬁlled with invariant closed curves

(one for each y value). In Figure 11.18, both axes are [⫺

␲

], so that one can

imagine the right and left boundaries to be glued together, and the same for the

top and bottom boundaries, to form the torus. The center of the square is the

origin, which is a ﬁxed point for the standard map.

The closed curves in Figure 11.18(a) are called KAM curves. KAM curves

ﬁgure importantly in understanding stability within area-preserving maps. This

stability analysis is the subject of KAM theory, a ﬁeld whose major advances are

due to the three mathematicians A. Kolmogorov, V. Arnold, and J. Moser. On

each of these curves, all points move with the same rate of rotation, called the

rotation number. The rotation number of a circle increases with y.

As the parameter a is increased from 0, other closed curves form that do

not wrap all the way around the torus. These KAM curves appear as oval-shaped

476

11.6 BIFURCATIONS IN P LANE M APS:AREA-PRESERVING C ASE

(a) (b)

(e) (f)

Figure 11.18 Standard maps at selected parameters.

Typical orbits of the standard family of maps S

(x, y) ⫽ (x ⫹ y mod 2

␲

, y ⫹ a sin(x ⫹

y)mod2

␲

) are shown for (x, y)in[⫺

␲

] ⫻ [⫺

␲

] and parameter values (a) a ⫽

0(b)a ⫽ 0.3(c)a ⫽ 0.6(d)a ⫽ 0.9(e)a ⫽ 1.2and(f)a ⫽ 7.0. In all but (f),

several orbits are plotted. In (f), one orbit is shown.

477

B IFURCATIONS

islands in Figure 11.18(b)–(e). Points on the closed curves are constrained to

map to the same closed curve. Each island in Figure 11.18(b)–(e) was made by

plotting a single orbit, which ﬁlls the curve densely. The KAM curves eventually

give way to irregular orbits. The last KAM curve that wraps around the torus can

be seen in the lower half of Figure 11.18(d). It disappears at a ⬇ 0.97.

✎ E XERCISE T11.14

Let S

denote the standard map.

(a) Show that for a ⬎ 0, the origin (0, 0) is a saddle ﬁxed point.

(b) For what values of a is (

␲

, 0) an elliptic ﬁxed point?

As a increases from zero, the invariant circles near y ⫽ 0 break up. We

see the stable and unstable manifolds of the saddle (0, 0) forming the boundary

between the closed curves surrounding the elliptic point and the closed curves

encircling the cylinder. A further increase in a shows regions of chaotic behavior

developing around these stable and unstable manifolds. New elliptic orbits come

into existence and disappear as chaotic regions expand to ﬁll an increasingly

larger space. Figure 11.18(f), at a ⫽ 7.0, shows no regions of stability. Only one

orbit is plotted.

➮ COMPUTER EXPERIMENT 11.2

The standard map can be made area-contracting by altering one term.

Deﬁne

a,b

(x, y) ⫽ (x ⫹ y(mod2

␲

),by⫹ a sin(x ⫹ y)(mod2

␲

)). (11.8)

Investigate S

a,b

for a ⫽ 4.0andb ⫽ 0.98. How many attracting periodic orbits

can you ﬁnd? (More than 100 exist for periods ⱕ 5.)

11.7 BIFURCATIONS IN DIFFERENTIAL

EQUATIONS

The main tool for analyzing the stability of periodic solutions of differential

equations is the Poincar

e map, which we ﬁrst deﬁned in Chapter 2. Let v be a

point in ⺢

, let f be a map deﬁned on ⺢

, and let

␥

be a periodic orbit of the

478

11.7 BIFURCATIONS IN DIFFERENTIAL E QUATIONS

autonomous differential equation

˙v ⫽ f(v). (11.9)

For a point v

␥

, the Poincar

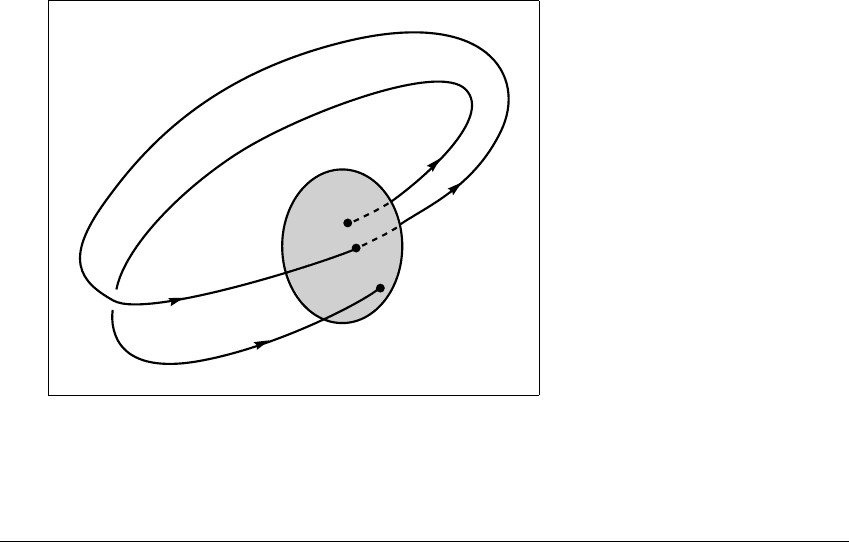
emapT is deﬁned on an n ⫺ 1 dimensional

disk D transverse to

␥

at v

. Figure 11.19 shows a periodic orbit for a ﬂow of

⺢

with a two-dimensional disk D. If v

is a point sufﬁciently close to v

on D,

then the solution through v

will follow close to

␥

until it intersects D again (the

ﬁrst return to D) at a point v

. This fact follows from continuous dependence

on initial conditions, Theorem 7.16. Let T(v

) ⫽ v

. (We may have to restrict

the domain of T to a smaller disk centered at v

in order to have the solution

hit D upon ﬁrst return.) For a periodic orbit of a planar differential equation, the

cross-sectional disk is a line segment transverse to the periodic orbit.

Notice that v

is a ﬁxed point or periodic point of T if and only if v

is on

a periodic orbit of (11.9). Thus we can investigate the stability of periodic orbits

through a linear analysis of T, by looking at the eigenvalues of D

T(v

Deﬁnition 11.17 The eigenvalues of the (n ⫺ 1) ⫻ (n ⫺ 1) Jacobian

matrix D

T(v

) are called the (Floquet) multipliers of the periodic orbit

␥

= T(v

)

Figure 11.19 A Poincar

emap.

The Poincar

e map, called T here, is deﬁned on a surface D which is transverse to

the ﬂow direction on a periodic orbit. The point v

on the periodic orbit maps to

itself under the Poincar

e map, while v

maps to v

479