Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

C ASCADES

main focus will be families of one-dimensional maps, such as the quadratic family,

and families of area-contracting planar maps, such as the H

enon family.

Cascades consist of stable periodic orbits and so are experimentally ob-

servable. An experimenter will only be able to see a few of these stages. Some

state-of-the-art examples of cascades in experiments are shown in Lab Visit 12.

Renormalization theory has been extremely successful in showing that it is

possible for the full inﬁnite sequence to exist. There are a number of regularities of

cascades, yielding universal numbers that are frequently observed in both physical

and numerical experiments. The chapter begins with the Feigenbaum constant,

one of these universal numbers. Challenge 12 is a more in-depth exploration of

this remarkable universal behavior.

12.1 CASCADES AND 4.669201609...

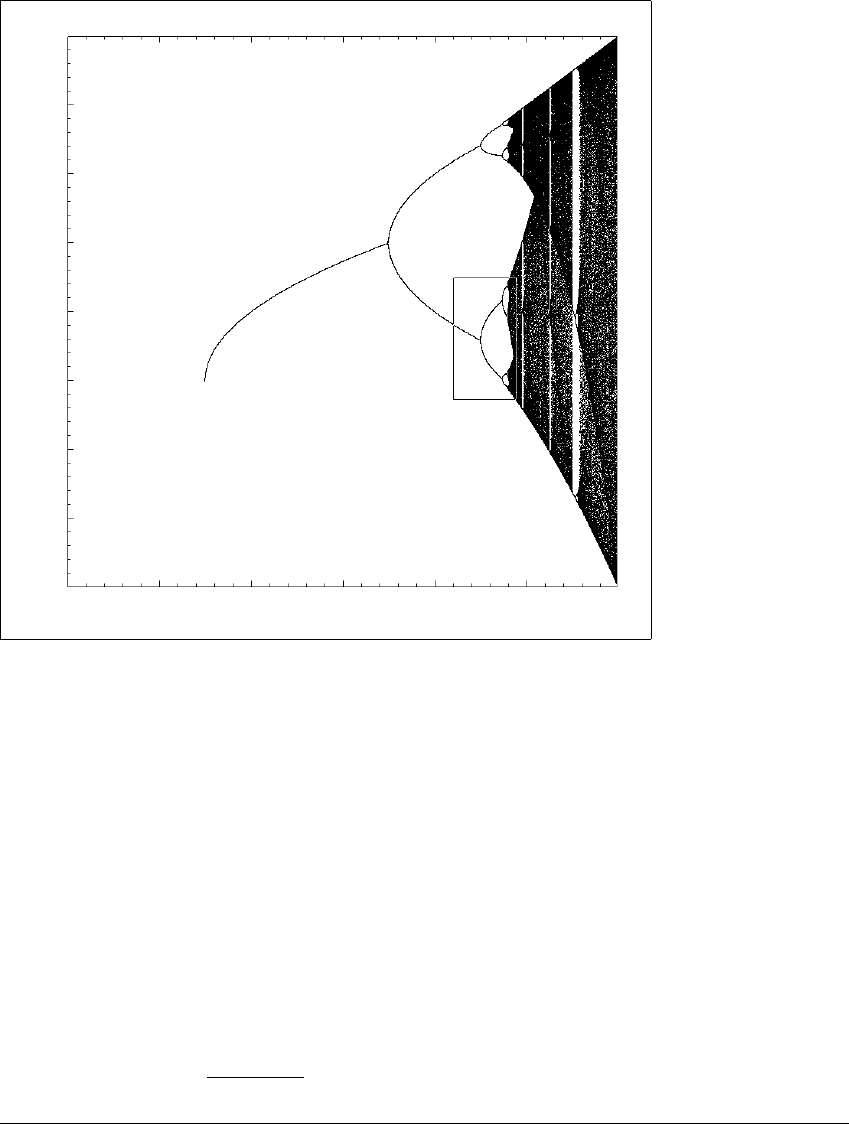
Figure 12.1 hints at the complexity present within a single bifurcation diagram.

The one-dimensional map used to generate the diagram is f

(x) ⫽ a ⫺ x

. Stable

periodic orbits of periods one, two, four, and eight are clearly visible in the

computer simulation. Factors of 2 beyond 8 are visible when the diagram is

magniﬁed.

In addition to the period-doublings that we can see in Figure 12.1, there are

inﬁnitely many that are not visible. Evidence of some of them can be seen in the

magniﬁcations of Figure 12.2. At a period-doubling bifurcation from a period-k

orbit, two branches of period-2k points emanate from a path of period-k points.

When the branches split off, the period-k points change stability (going from

attractor to repeller, or vice versa). This change is detected in the derivative of

which, when calculated along the path of ﬁxed points, crosses ⫺1.

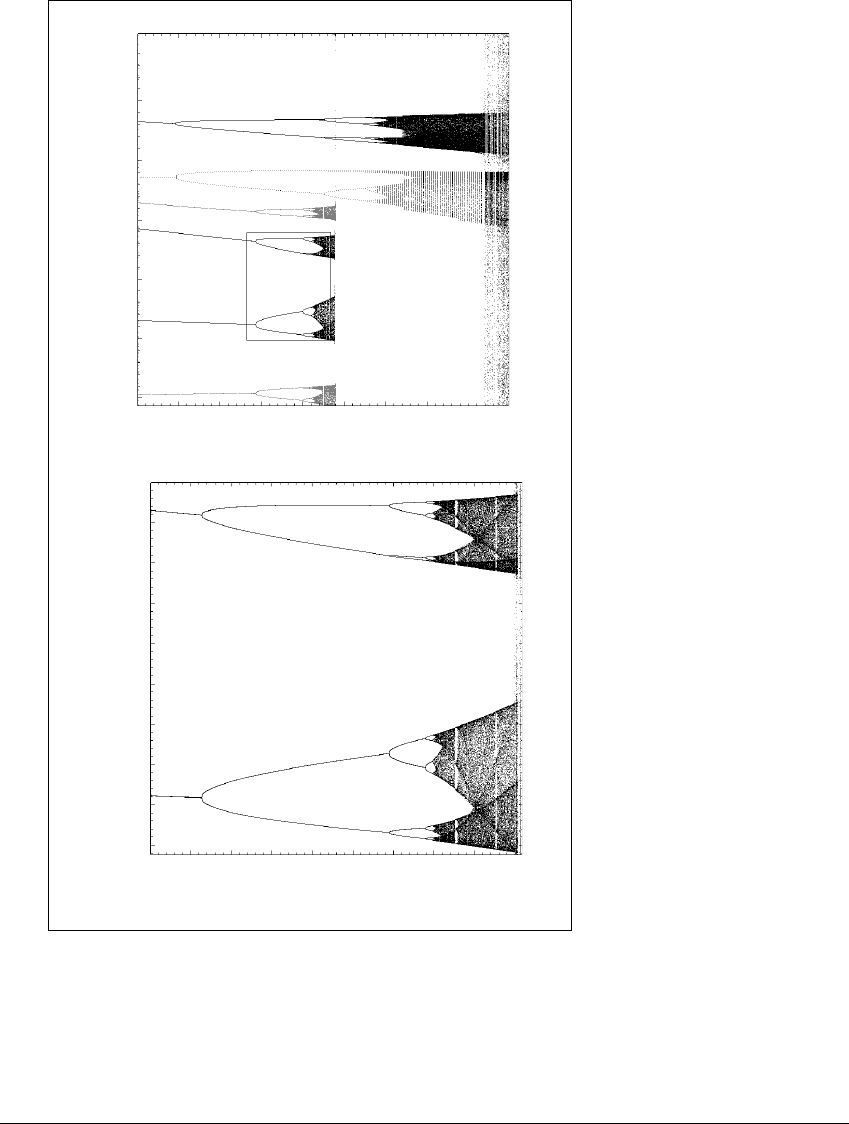
Figure 12.2(a) shows a magniﬁed view of the box drawn in Figure 12.1, and

together with the further magniﬁcation in Figure 12.2(b), shows period-doubling

bifurcations up to period 64. A period-doubling cascade can also occur from a

periodic orbit of higher period. Magniﬁcations of the period three window of

Figure 12.1 are shown in Figure 12.2(c) A cascade beginning with sinks of periods

3, 6, 12,...can be seen. In Figure 12.2, the period ﬁve cascade exhibits sinks of

periods 5, 10, 20,....

The series of bifurcation diagrams shown in Figure 12.1, 12.2(a) and (b)

suggests a scaling behavior in the cascade of the quadratic map. In 1978, M. Feigen-

baum noted that the ratios of parameter distance between two successive period-

500

12.1 CASCADES AND 4.669201609. . .

⫺2

⫺1 a 2

Figure 12.1 Bifurcation diagram for the one-dimensional quadratic family

(

) ⴝ

ⴚ

The variable x is on the vertical axis, and the bifurcation parameter a is on the

horizontal axis. When a is ﬁxed at a value less than ⫺1 4, the orbits of all initial

conditions diverge to ⫺

⬁

. There is a saddle-node bifurcation at a ⫽⫺1 4, at which

a period-one sink is created. It persists for ⫺1 4 ⬍ a ⬍ 3 4. At a ⫽ 3 4, the period-

one sink loses stability and is replaced with a period-two sink in a period-doubling

bifurcation. Higher values of a show further bifurcations that create more complex

attractors. For a ⬎ 2 there are no attractors.

doublings approach a constant as the periods increase to inﬁnity. Moreover, this

constant is universal in the sense that it applies to a variety of dynamical systems.

Speciﬁcally, if the nth period-doubling occurs at a ⫽ a

, then

lim

n→

⬁

n⫺1

⫺ a

n⫺2

⫺ a

n⫺1

⫽ 4.669201609 ..., (12.1)

501

C ASCADES

0.25

⫺0.636

1.1 a 1.45

(a)

0.037

⫺0.121

1.383 a 1.406

(b)

⫺2

1.74 a 1.8

(c)

1.62 a 1.64

(d)

Figure 12.2 Universal behavior in the quadratic family.

(a) The box drawn in Figure 12.1 is enlarged to show many similarities to the full-

size diagram. Cascades occur on increasingly ﬁne scales. (b) Enlargement of the box

in (a). (c) The period-three window in the quadratic family shows period-doubling

cascades. (d) The period-ﬁve window.

a number now known as Feigenbaum’s constant. Surprisingly, the limit is the

same for any one-parameter family of unimodal maps with negative Schwarzian

derivative. The ﬁrst proof that this limit exists was given in (O. Lanford, 1982).

Table 12.1 shows a list of the parameters at which period-doublings occur

in the quadratic map f(x) ⫽ a ⫺ x

. The ﬁxed point bifurcates into a ﬁxed saddle

502

12.1 CASCADES AND 4.669201609. . .

Period Parameter

Ratio

2 0.75

4 1.25

8 1.3680989 4.2337

16 1.3940462 4.5515

32 1.3996312 4.6458

64 1.4008287 4.6639

128 1.4010853 4.6682

256 1.4011402 4.6689

Period Parameter

Ratio

3 1.75

6 1.7685292

12 1.7772216

24 1.7792521 4.2810

48 1.7796964 4.5698

96 1.7797923 4.6363

192 1.7798129 4.6524

Table 12.1 Feigenbaum’s constant in the quadratic map.

(a) A list of parameters a

at which the nth period-doubling bifurcation occurs in

the period-one cascade, along with the ratio (a

n⫺1

⫺ a

n⫺2

) (a

⫺ a

n⫺1

). (b) Same

for a period-three cascade of the quadratic map.

and a period-two attractor at a ⫽ 0.75, followed by a cascade of period-doublings.

Also shown are the bifurcation values for the period-three cascade of the quadratic

map.

A computer program to ﬁnd the bifurcation parameter values uses a binary

search method. To begin the determination of a period-doubling bifurcation value,

say from period four to period eight, two values of the parameter a are chosen

that bracket the bifurcation point. The period of the orbit at the midpoint of

the bracketing interval is determined using the following simple method. First,

a long trajectory is created, in order to approach the current attracting orbit as

closely as possible. The period of the orbit is tested by comparing the current

point to later iterates of the point, within a small tolerance. When the period is

determined, either four or eight, the midpoint becomes a new endpoint of the

bracketing interval, replacing the endpoint that has the same period. The length

of the bracketing interval has been cut in two. By repeating this process, accurate

estimates of the bifurcation values of a cascade can be determined.

Table 12.2 contains a list of bifurcation values for two other cascades. Note

that the ratio (12.1) is repeated for the one-dimensional logistic family as well

as for the two-dimensional H

enon family. This version of the H

enon map, given

by f(x, y) ⫽ (a ⫺ x

⫺ 0.3y, x), is orientation-preserving (has positive Jacobian

determinant).

503

C ASCADES

Period Parameter

Ratio

2 3.0000000

4 3.4494896

8 3.5440903 4.7514

16 3.5644073 4.6562

32 3.5687594 4.6683

64 3.5696916 4.6686

128 3.5698913 4.6692

256 3.5699340 4.6694

Period Parameter

Ratio

2 1.2675000

4 1.8125000

8 1.9216456 4.9933

16 1.9452006 4.6337

32 1.9502644 4.6516

64 1.9513504 4.6630

128 1.9515830 4.6678

256 1.9516329 4.6688

Table 12.2 Feigenbaum’s constant in the logistic map and H

enon map.

(a) Parameter values of period-doubling bifurcations for f(x) ⫽ ax(1 ⫺ x). (b) The

ratio also approaches Feigenbaum’s constant for the H

enon map.

➮ COMPUTER EXPERIMENT 12.1

Locate the period-doubling cascade for the orientation-reversing H

enon

map f(x, y) ⫽ (a ⫺ x

⫹ 0.3y, x). Start with a ⫽ 0 and the ﬁxed point (x, y) ⫽

(0, 0). Calculate the ratio of successive period-doubling intervals as in Table 12.2.

12.2 SCHEMATIC BIFURCATION DIAGRAMS

Figure 12.3 shows cascades in the development of four distinct chaotic attractors

occurring in the Poincar

e map of the forced, damped pendulum. Notice that

the attractors are simultaneously present for a certain range of the parameter.

Studying the dynamics here is complicated by the fact that we have no explicit

formula for the underlying Poincar

e map. Our aim in this section is to develop a

methodology for efﬁcient analysis of bifurcation diagrams—to give a road map of

essential features, even when the underlying equations are unknown.

It is convenient to think of a schematic “tinker toy” model, consisting

of “sticks” and “sockets”, for the periodic orbits in our bifurcation diagrams.

The “sticks” are paths of hyperbolic orbits, all of one type—stable or unstable,

while the “sockets” are bifurcation orbits. For the remainder of this chapter, we

characterize hyperbolic orbits as stable or unstable, allowing the reader to translate

these words within the particular system of interest. For one-parameter families

of one-dimensional maps, the stable hyperbolic orbits are periodic sinks, while

504

12.2 SCHEMATIC B IFURCATION D IAGRAMS

␲

⫺

␲

2.60 2.78

(a)

⫺0.211

⫺2.040

2.653 2.693

(b)

Figure 12.3 Period-doubling cascades in the forced, damped pendulum.

(a) The development of four chaotic attractors is shown, in four varying shades

of gray/black. Each of two period-two sinks at the bottom of the diagram evolve

through period-doublings to a two-piece chaotic attractor. Two ﬁxed-point sinks at

the top evolve to one-piece chaotic attractors. Several crises can be observed. (b) A

magniﬁcation of the one of the cascades beginning from a period-two sink is shown.

505

C ASCADES

the unstable hyperbolic orbits are periodic repellers. For one-parameter families

of area-contracting planar maps, stable orbits are periodic sinks, while unstable

orbits are saddles. These two examples are the primary settings in which we

observe cascades in this chapter.

We will ﬁnd our bookkeeping simpliﬁed by considering the several points

of a periodic orbit as a single entity. This point of view sacriﬁces little, since our

primary focus is on the stability of the orbit, which is a collective property. Recall

that in order to determine the stability of a periodic orbit, all points in the orbit—

together with their derivatives (or Jacobian matrices)—must be calculated. For

example, assume that x

is a period-two point of f: f(x

) ⫽ x

and f(x

) ⫽ x

In order to ﬁnd out the stability of the orbit, we must compute the eigenvalues of

) ⫽ Df(x

)Df(x

). Lemma 2 in Appendix A implies that the eigenvalues

of Df(x

)Df(x

) are identical to the eigenvalues of Df(x

)Df(x

) ⫽ Df

). In

the one-dimensional case (see, for example, the Stability Test for periodic orbits

in Section 1.4), the derivative (f

)



is the same when evaluated at any of the k

points in a period-k orbit.

Therefore, we will think of a periodic orbit as a single object, with all points

in the orbit being represented by one point in our schematic model. The phrase

“derivative of a periodic orbit” will refer to the derivative of f

with respect to x

evaluated at any point in the orbit. (For phase space dimensions greater than one,

this phrase will have to be interpreted appropriately as an eigenvalue of D

We always take k to be the minimum period of the orbit.

Figure 12.4 is a guide to the various types of periodic orbits we will encounter

in cascades. An unstable periodic point p of period k is called a regular repeller

if (f

)



(p) ⬎ 1; it is called a ﬂip repeller if (f

)



(p) ⬍⫺1. In other words, we

have partitioned the set of hyperbolic periodic orbits into three subsets: stable,

regular unstable, and ﬂip unstable. We call these sets S (for stable), U

⫹

(for

regular unstable), and U

⫺

(for ﬂip unstable). Deﬁnition 12.1 makes precise what

the “sticks” are in our tinker-toy model.

Deﬁnition 12.1 A maximal path of hyperbolic ﬁxed points or periodic

orbits is called a schematic branch (or just branch). In the case of a schematic

branch of periodic orbits, one point on the branch represents all points in one

orbit.

Figure 12.4(b) shows the bifurcation diagram of a family of maps with

a period-three saddle node and a period-doubling bifurcation from the path of

stable period-three orbits. A schematic bifurcation diagram representing the same

family appears in (c), with the bifurcation orbits drawn as circles. The saddle node

bifurcation is indicated schematically by a circle with a plus sign (⫹) inside it,

506

12.2 SCHEMATIC B IFURCATION D IAGRAMS

Saddle-node bifurcation

Period-doubling bifurcation

Branch of stable orbits

Branch of regular unstable orbits

Branch of flipped unstable orbits

e = +1

|e| < 1

e > 1

e < -1

e = -1

DESCRIPTIONNOTATION EIGENVALUE

(a)

(b) (c)

Figure 12.4 Elements of schematic diagrams.

(a) A saddle-node bifurcation is indicated schematically by a circle with a plus sign

(⫹) inside it. The saddle node orbit has derivative ⫹ 1 (or one eigenvalue equal

to ⫹1, in two or more dimensions). A period-doubling bifurcation is drawn with

aminussign(⫺). The map has derivative ⫺1 (or one eigenvalue equal to ⫺ 1) at

this orbit. Solid segments represent branches of stable orbits or branches of regular

unstable orbits, with the branches of stable orbits directed with an arrow pointed to

the right and the branches of regular unstable orbits directed to the left. All points

in an orbit are represented by one point in the schematic diagram. The dashed

schematic branch represents the three paths of ﬂip unstable orbits. Regular unstable

orbits have exactly one eigenvalue larger than ⫹1, while ﬂip unstable orbits have

exactly one eigenvalue smaller than ⫺1. The absolute values of all eigenvalues of

a stable orbit are smaller than 1. (b) The bifurcation diagram of a family of one-

dimensional maps with a period-three saddle node at a ⫽ a

and a period-doubling

bifurcation at a ⫽ a

from the stable period-three orbit is shown. A stable period-six

orbit appears at a

. (c) A schematic bifurcation diagram representing the family in

(b). The number next to a schematic branch represents the period of orbits on the

branch.

507

C ASCADES

representing the ⫹1 derivative of that orbit, while the period-doubling bifurcation

is drawn with a minus sign (⫺). A saddle node of period three occurs in the logistic

family for a slightly less than 3.83. The bifurcation diagram for this family is given

in Figure 1.7(b).

Notice that emanating from the saddle node in Figure 12.4(c) there are

two solid schematic branches: one branch, with an arrow directing it to the right,

represents all three paths of stable period-three orbits in (b); the other branch,

directed to the left represents the three paths of unstable U

⫹

orbits in (b).

Emanating from the period-doubling bifurcation orbit in (c) is a solid schematic

branch directed to the right, representing the six paths of stable period-six orbits

in (b). (The rationale for putting arrows on the branches is not apparent now,

but will become clear in Section 12.3.) The dashed schematic branch represents

the three paths of U

⫺

orbits in (b).

✎ E XERCISE T12.1

Why do the three period-doubling bifurcation points in Figure 12.4(b) occur

at the same parameter value?

In schematic diagrams, such as Figure 12.4, points on the branches represent

ﬁxed points or periodic orbits that are isolated. As we saw in Chapter 11, if p is a

hyperbolic ﬁxed point of f, then there is a neighborhood N in phase space that

excludes other ﬁxed points. What about higher-period orbits? Since p is also a

ﬁxed point of f

, and (f

)



(p) ⫽⫹1, there is a neighborhood N

in phase space

(perhaps smaller than N)suchthatp is the only ﬁxed point of f

in N

;thatis,

there are no period-k points in N

✎ E XERCISE T12.2

Assume that p is a hyperbolic ﬁxed point. Let 兵p

其 be a sequence of periodic

points such that p

→ p, and, for each n, let t

be the (minimum) period of

. Explain why lim

n→

⬁

⫽

⬁

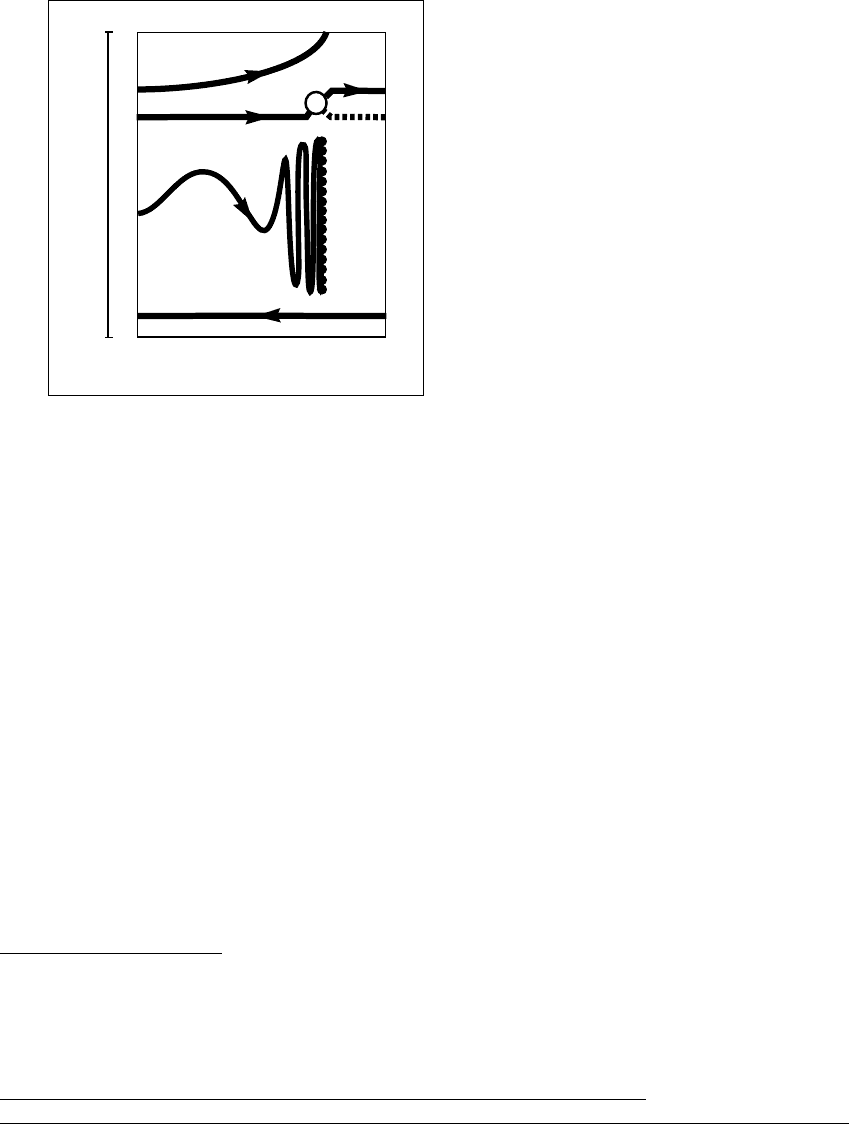
How do schematic branches end? Suppose we try to follow the branch

containing a particular hyperbolic ﬁxed point at a ⫽ a

. Let G be the portion

of this branch in [a

⬁

) ⫻ ⺢. Figure 12.5 shows portions of four such schematic

branches. Now assume that there exists a parameter value a

, with a

⬎ a

, such

that G does not extend to a

. What can happen to G between a

and a

?One

possibility is that G may become unbounded in x-space. In other words, the

508

12.2 SCHEMATIC B IFURCATION D IAGRAMS

Figure 12.5 How schematic branches can end.

Schematic branch G

leaves the compact region V ⫻ [a

] through the boundary

of V;branchG

ends in a period-doubling bifurcation; branch G

ends in a line

segment of ﬁxed points; and G

extends through the parameter interval [a

absolute values of points on G go to inﬁnity as or before G reaches a

. Otherwise,

there exists a bounded set V in x-space such that G remains in V; G 傺 [a

] ⫻ V.

Since G is a path, it is deﬁned as the graph of a function

␾

: J → V, where

J is an interval of real numbers. That is, G ⫽ 兵(a,

␾

(a)) : a 僆 J其. It follows that

there exists a parameter value a

such that [a

) 傺 J 傺 [a

]. We argue that

J is open-ended on the right side. Suppose, on the contrary, that J contains the

endpoint a

. Then G has at least one ﬁxed point p at a ⫽ a

, according to Exercise

T12.3. Since p is hyperbolic, G must extend beyond a

(by Deﬁnition 11.6 and

Theorem 11.7, Chapter 11), a contradiction.

The “half-branch” G must have at least one limit point at a

. By continuity

of the map, this point (or points) is ﬁxed. By the above argument, any limit

points of G that are not in G must be nonhyperbolic. Depending on the map,

these nonhyperbolic ﬁxed points may or may not be bifurcation orbits.

✎ E XERCISE T12.3

(a) Show that if G is a path of ﬁxed points deﬁned on [a

), and if

G is bounded, then G has at least one limit point at a ⫽ a

. (b) Show that

any limit points of G are ﬁxed points.

509