Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems
Подождите немного. Документ загружается.


C ASCADES
Figure 12.5 shows the fate of several schematic branches in a closed,
bounded region [a
0
,a
1
] ⫻ V:(1)G
1
leaves [a
0
,a
1
] ⫻ V through the boundary
of V;(2)G
2
ends in a bifurcation orbit from which other branches emanate;
(3) G
3
ends in an interval of fixed points; and (4) G
4
extends through the pa-
rameter interval [a
0
,a
1
]. We will concentrate below on families of maps where
the nonhyperbolic fixed points and periodic orbits are all saddle-node or period-
doubling bifurcations, thereby ruling out the fate of branch G
3
.
12.3 GENERIC BIFURCATIONS
The word “generic” refers to behavior that is typical—behavior that we normally
expect to see. In this section we explain the fact that for families of smooth maps
on the real line, it is a generic property that the map has only saddle-node and
period-doubling bifurcations. The point is that these two are the most commonly-
seen bifurcations, and that other “nongeneric” bifurcations such as the pitchfork
bifurcation occur rarely.
We will say that a property of smooth functions is generic if the set of
functions that have the property is dense. This means that for each smooth f,
whether it has the property or not, arbitrarily small perturbations of f have the
property. We caution the reader that the term “generic” is often used in a more
specialized form in the mathematical literature; consult a topology book for more
details. In any case, the specialized usage implies the usage in this book.
An example of a generic property of smooth functions f :[0, 1] → ⺢ is that
the function has at most a finite number of zeros. (A zero of f is a number x for
which f(x) ⫽ 0.) Not every smooth function has this property: The identically zero
function has uncountably many. But functions arbitrarily close to the identically
zero function, namely the constant functions f(x) ⬅
⑀
for small
⑀
, have no zeros.
To show that this property is generic we need to find that these neighbors exist
for any smooth function.
Before we check this fact, we mention another generic property. Let x
0
be
a number in [0, 1], and consider functions f with the following property:
(G
0
) f :[0, 1] → ⺢ and f
(x
0
) ⫽ 0 whenever f(x
0
) ⫽ 0.
Note that if f(x
0
) ⫽ 0andf
(x
0
) ⫽ 0, then there is some neighborhood of x
0
in
which it is the only zero. In fact, the Mean Value Theorem implies that
f(x) ⫽ f(x) ⫺ f(x
0
) ⫽ f
(c)(x ⫺ x
0
) ⫽ 0
for x close to but not equal to x
0
,sincec is trapped between x and x
0
,and
f
(x
0
) ⫽ 0.
510

12.3 GENERIC B IFURCATIONS
Notice that (G
0
) implies that f has at most a finite number of zeros in a
bounded set. If there were infinitely many zeros, we could choose a sequence x
i
of
zeros that converges to some point
x in [0, 1], which would also have to be a zero
by the continuity of f. Because f satisfies (G
0
), f(x) ⫽ 0andf
(x) ⫽ 0, so that
there must be some neighborhood of
x in which it is the only zero, a contradiction.
It remains to explain why (G
0
) is a generic property. This follows from
Theorem 12.2, which can be found in (Hirsch, 1976). For a smooth function f,a
critical point c satisfies f
(c) ⫽ 0.
Theorem 12.2 (Sard’s Theorem) Let f :[0, 1] → ⺢ be a smooth function,
and let C denote the set of critical points of f. Then f(C) has measure zero.
In this terminology, a function has the property (G
0
) if and only if 0 does not
belong to f(C). The function g
⑀
(x) ⫽ f(x) ⫹
⑀
has the same critical points as f(x).
Since f(C) has measure zero, g
⑀
has property (G
0
) for almost every real number
⑀
, including values of
⑀
arbitrarily near 0. Therefore functions g
⑀
arbitrarily near
f are in (G
0
), even if f isn’t. This proves that property (G
0
) is a generic property
of smooth functions.
✎ E XERCISE T12.4
Let g : ⺢ → ⺢ be a smooth map, and assume that for each x, g(x) ⫽ 0
implies g
(x) ⫽ 0. Show that there are at most finitely many zeroes (points
x for which g(x) ⫽ 0) in any bounded interval.
Another generic property for smooth functions h is
(G
1
) h :[0, 1] → ⺢ and h
(x
0
) ⫽ 0 whenever h
(x
0
) ⫽ 0.
Such a function h always has the property that there are only a finite number of
x
0
for which h
(x
0
)is0.
Next we look at a slightly different class:
(G
2
) k :[0, 1] → ⺢ and k
(x
0
) ⫽ 0 whenever k
(x
0
) ⫽ 1.
We can use this property to study certain bifurcation diagrams. Notice that if
k(x) satisfies (G
2
), then h(x) ⫽ x ⫺ k(x) satisfies (G
1
). Also (G
2
) guarantees that
there are at most finitely many points x
0
at which k
(x
0
) ⫽ 1.
We can also talk about generic properties of functions k
a
(x) that depend on
a parameter. Define
k
a
(x) ⫽ x ⫹ a ⫺ h(x),
511
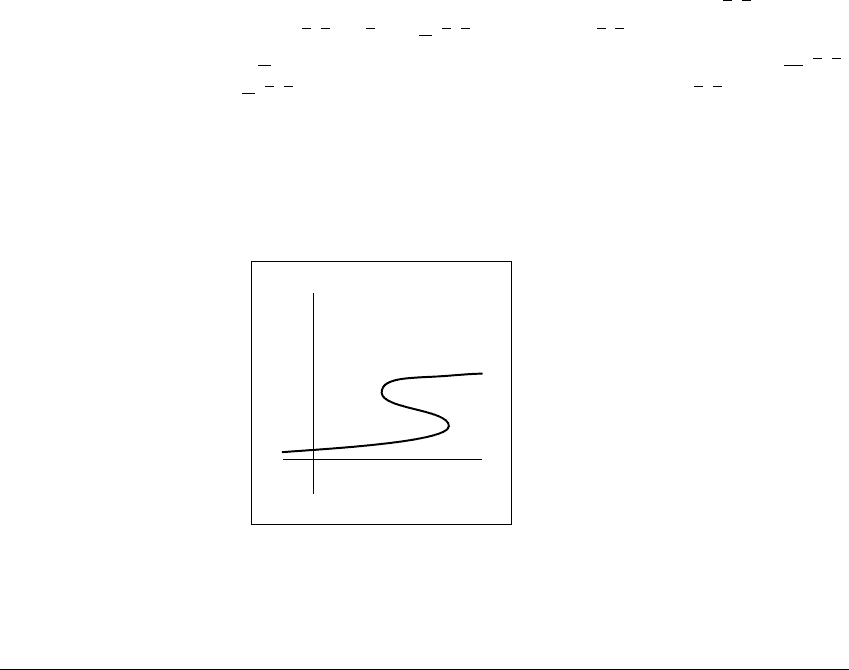
C ASCADES
where h satisfies (G
1
). This is a rather special map depending on a parameter
because a enters in a very simple way. Nonetheless, it is instructive because we
can determine what the bifurcation diagram for fixed points of k must look like.
In the bifurcation diagram, we plot the set 兵(a, x)其 of points at which k
a
(x) ⫽ x.
This set is just 兵(h(x),x)其, the graph of h(x) reflected about the 45
◦
line:
If we set a ⫽ h(x) for a particular x, then (a, x) is on the graph of h and also
k
a
(x) ⫽ x. (Here we are ignoring all periodic orbits of period greater than 1.)
At the saddle-node bifurcation points (a, x),k
a
(x) ⫽ x and the partial derivative
k
a
x(x) ⫽ 1. Figure 12.6 shows the bifurcation diagram of fixed points for the
function k, when h(x) ⫽ x
3
⫺ 9x
2
⫹ 24x ⫺ 12. Notice that the saddle nodes of k
are the relative maximum and/or minimum points of h on the graph of a ⫽ h(x).
Since h satisfies (G
1
), there are only a finite number of these points in a bounded
region of (a, x)-space.
We have described one generic property of bifurcation orbits—namely,
that there cannot be infinitely many (fixed-point) saddle nodes in a bounded
region—and that argument is given for only a special set of maps. More generally,
let f : ⺢ ⫻ ⺢ → ⺢ be a smooth family of scalar maps, and let (
a, x) be a point
for which f(
a, x) ⫽ x and
f
x
(a, x) ⫽ 1; that is, (a, x) satisfies the conditions on
f and
f
x
necessary for a saddle node. If we specify further that both
2
f
x
2
(a, x)
and
f
a
(a, x) are nonzero, then there is a neighborhood of (a, x) in which it is
the only (fixed-point) saddle node. (This property is verified in Theorem 11.9.)
There are also conditions on the partial derivatives of f that guarantee that a
given period-doubling bifurcation point will be similarly isolated from other such
bifurcations of the same or lower period. (See Exercise 11.9 for these conditions.)
a
x
Figure 12.6 The bifurcation diagram of fixed points of
k
a
(
x
) ⴝ
x
ⴙ
a
ⴚ
h
(
x
)
,
where
h
(
x
) ⴝ
x
3
ⴚ 9
x
2
ⴙ 24
x
ⴚ 12
.
The saddle node fixed points of k are the local maximum and minimum points of
a ⫽ h(x).
512

12.3 GENERIC B IFURCATIONS
Thus we can conclude that having only a finite number of fixed point saddle-node
and period-doubling bifurcations in a bounded region of (a, x)-space is a generic
property. In particular, any smooth one-parameter family either has this property
or can be closely approximated by a family that has it. By “closely approximated”,
we mean that a family g can be chosen so that sup
(a,x)僆⺢⫻⺢
| f(a, x) ⫺ g(a, x) |
is as small as we like. The proof that the set of one-parameter families described
below is generic (within the class of maps whose orbits have at most one unstable
direction) is due to (Brunovsky, 1969).
Recall that a branch of orbits is a maximal path (in a) of hyperbolic fixed
points or periodic orbits and that branches end only in nonhyperbolic orbits. For
one-dimensional maps, nonhyperbolic fixed points have derivatives equal to ⫹1
or ⫺1. We denote these sets of orbits by B
⫹
and B
⫺
, respectively. For higher-
dimensional maps, the set B
⫹
contains fixed points with exactly one eigenvalue
equal to ⫹1 and no other eigenvalues on or outside the unit circle, whereas the set
B
⫺
contains fixed points with exactly one eigenvalue equal to ⫺1 and no other
eigenvalues on or outside the unit circle. (By restricting B
⫹
and B
⫺
in maps of
dimensions greater than one in this way, we are saying that nonhyperbolic fixed
points can have at most one eigenvalue of absolute value greater than or equal
to one.) So far we have ignored the cases in which an orbit is in B
⫹
or B
⫺
and a
bifurcation does not occur, or the cases where nonhyperbolic fixed points are not
isolated.
By assuming the following hypotheses, we require that all nonhyperbolic
fixed points be either saddle-node or period-doubling bifurcations.
Definition 12.3 (Generic Bifurcation Hypotheses.)
(1) When p is in B
⫹
, then p is a saddle-node bifurcation orbit. Specifically,
at an orbit in B
⫹
two branches of orbits emanate: one branch of orbits in S
(stable orbits) and one branch of orbits in U
⫹
(regular unstable orbits). Orbits
on both branches have the same period as the bifurcation orbit. In a bifurcation
diagram (representing a compact subset of the domain), for each k, there are only
finitely many orbits in B
⫹
. Schematic diagrams of all the generic saddle-node
bifurcations are shown in Figure 12.7.
(2) When p is in B
⫺
, then p is a period-doubling bifurcation orbit. At an
orbit in B
⫺
, three branches of orbits emanate. See Figure 12.4. Orbits on one of
the branches have twice the period of the bifurcation orbit. Orbits on the other
two branches have the same period: One of these two branches has orbits in S
(stable orbits) and the other has orbits in U
⫺
(flip unstable orbits). Again, in
the bifurcation diagram, for each k, there are only finitely many orbits in B
⫺
.
Schematic diagrams of all the generic period-doubling bifurcations are shown in
Figure 12.10.
513

C ASCADES
k
k
U
+
S
+
k
k
U
+
S
+
(a) (b)
Figure 12.7 The generic saddle-node bifurcations.
At a period-k saddle node, two branches of orbits emanate: one branch contains
stable (S) orbits and the other contains regular unstable (U
⫹
) orbits. All orbits on
both branches are period-k orbits. (a) The two branches appear to the right of the
bifurcation parameter a ⫽ a
⫹
; orbits on the branches exist for a greater than (and
near) a
⫹
. (b) The two branches appear to the left of a
⫹
.
We will call a one-parameter family of maps generic if it satisfies these
restrictions on orbits in B
⫹
and B
⫺
. The saddle-node and period-doubling bifur-
cations are called generic bifurcations.
Generic maps form a large set in that they are dense in the set of one-
parameter families of maps. Although other situations are possible (such as pitch-
fork bifurcations or orbits in B
⫹
or B
⫺
not being bifurcation orbits), they are not
likely to occur. And if they do, there will be closely approximated by a family
whose only bifurcations are saddle-node and period-doubling bifurcations.
For one-dimensional families, saddle-node bifurcation orbits connect
schematic branches of stable orbits and regular unstable orbits. What types of
schematic branches emanate from period-doubling bifurcation orbits? Following
a path of fixed points through a period-doubling bifurcation, the derivative (or
an eigenvalue) goes through ⫺1 (either smaller to larger or vice versa) at the
bifurcation orbit. Therefore, one branch of fixed points is stable (derivative has
absolute value smaller than one) and the other is flip (derivative smaller than
⫺1). To determine the third branch, the doubled-period branch, we appeal to a
description of the graph of the function f
2
a
near the bifurcation point, as shown
in Figure 12.8. As a branch of stable fixed points nears a period-doubling bifur-
cation (Figure 12.8(a)), the derivative of f
2
a
evaluated at orbits along the branch
approaches ⫹1. After the derivative has crossed ⫹1 (Figure 12.8(b)), there are
three fixed points. From the direction that the graph crosses the line y ⫽ x, we see
that there are two new paths of stable fixed points. Suppose, on the other hand,
that a single branch of flip fixed points approaches a period-doubling bifurcation
514
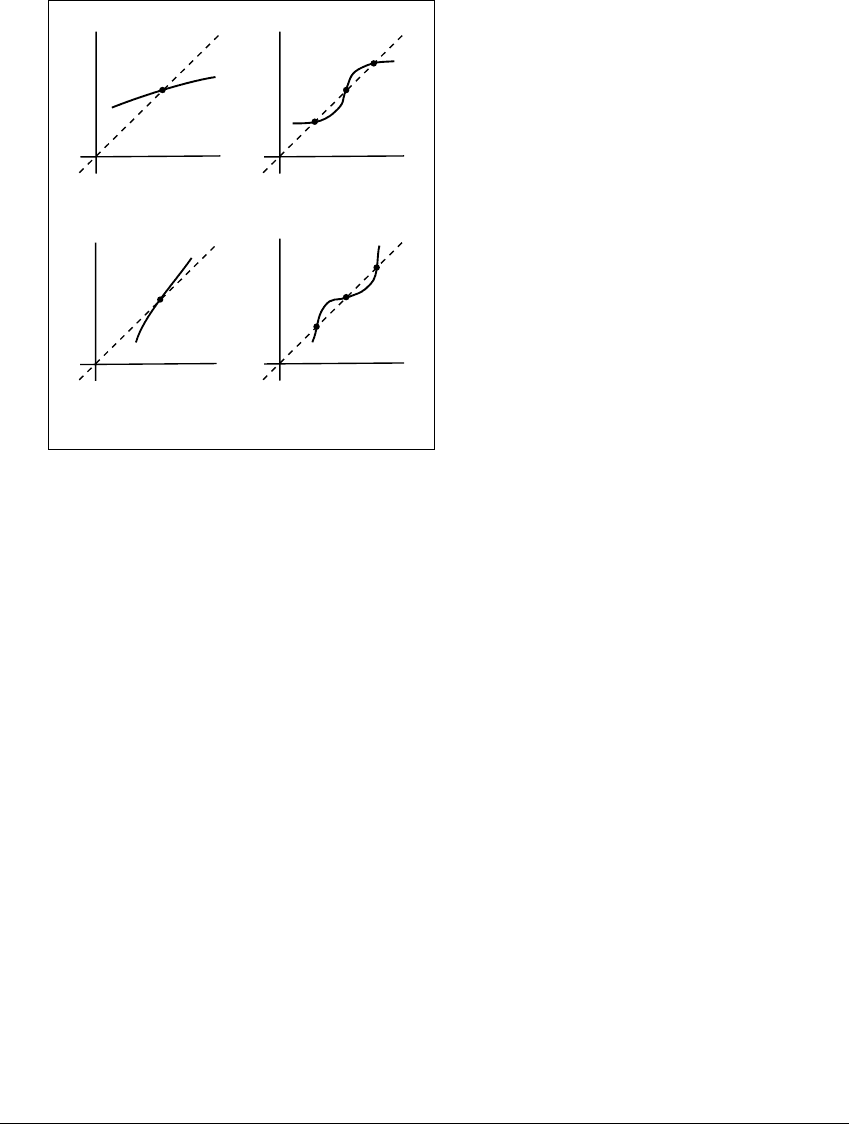
12.3 GENERIC B IFURCATIONS
x
y
x
y
(a) (b)
x
y
x
y
(c) (d)
Figure 12.8 Graphs of
f
2
a
as the function undergoes period-doubling bifurca-
tions.
Since the map f
a
has slope ⫺1 at a period-doubling bifurcation, the slope of the
second iterate f
2
is ⫹1. If the parameter value a is chosen on one side of the
bifurcation, as shown in (a), then the graph of f
2
looks like (b) for parameter values
on the other side of the bifurcation. Similarly, the graph of f
2
may change from (c)
to (d) at the bifurcation point.
(Figure 12.8(c)). Looking again at the graph of f
2
a
and at its direction of crossing
at each intersection with the line y ⫽ x, we conclude that the continuation of
the branch of flip fixed points after the bifurcation (Figure 12.8(d)) is a stable
branch, while the two new paths of fixed points are regular unstable orbits.
We summarize these facts in Lemma 12.4.
Lemma 12.4 (Exchange of Stability Principle.) At a period-doubling
bifurcation orbit of period k occurring at a ⫽ a
b
, one period-k branch emanating
from the bifurcation orbit contains flip unstable orbits and the other period-k
branch consists of stable orbits; for one branch, a ⬍ a
b
, and for the other, a ⬎ a
b
.
If the period-2k branch lies on the same side as the period-k stable branch, then it
has regular unstable orbits, while if it lies on the opposite side, it has stable orbits.
Although we do not prove this lemma, justification for one-dimensional
families follows from diagrams of the possible generic period-doublings shown in
Figure 12.9. For two-dimensional families, index theory is needed.
515
C ASCADES
k
2k
k
S
S
U
-
k
2k
k
S
S
U
-
(a) (b)
k
2k
k
S
U
-
U
+
k
2k
k
S
U
-
U
+
(c) (d)
Figure 12.9 The generic period-doubling bifurcations for families of one-
dimensional maps.
Bifurcation diagrams of all possible generic period doublings from period-k to period-
2k are shown. A single point of each period-k orbit appears, together with two points
for each period-2k orbit. The arrows indicate whether nearby points move toward
or away from the periodic points.
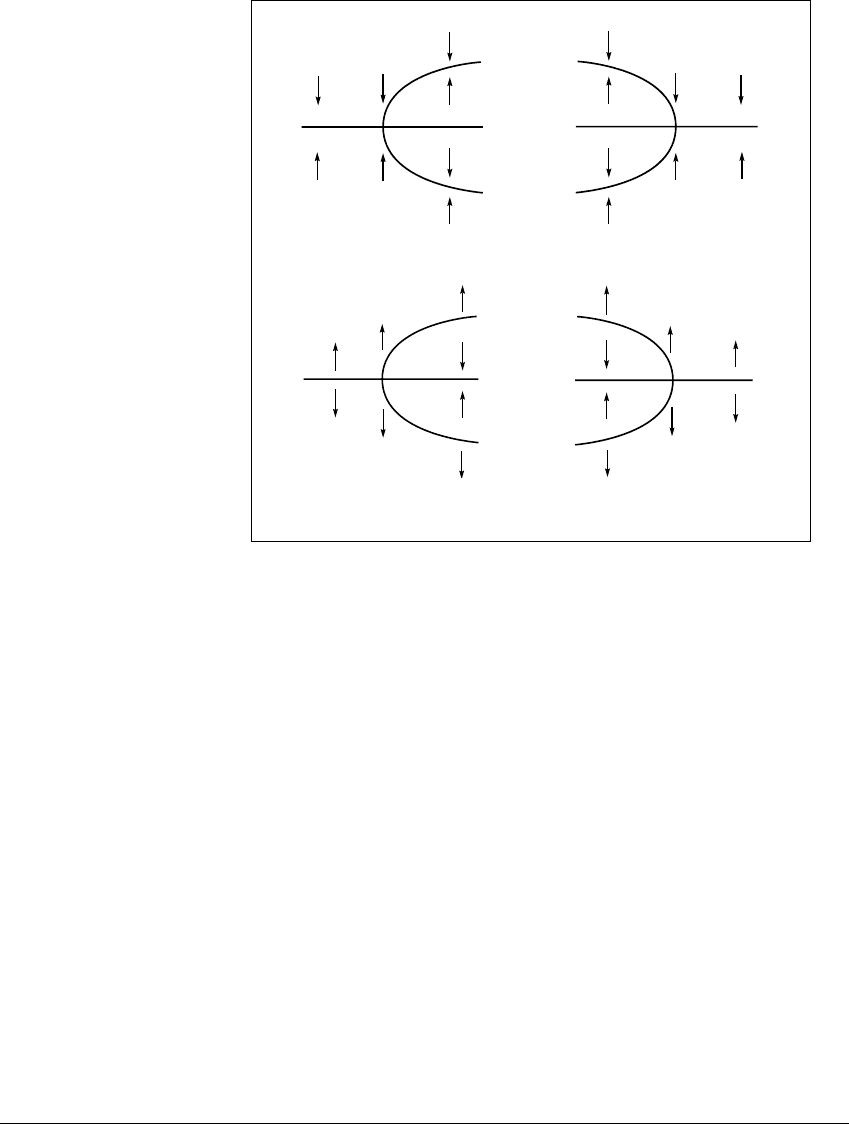
Figure 12.10 shows the possible period-doubling bifurcations under the
Generic Bifurcation Hypotheses of Definition 12.3. Again, branches of orbits
in S are represented by solid line segments with arrows directed to the right,
while branches of orbits in U
⫹
are represented by solid line segments with arrows
directed to the left. Branches of orbits in U
⫺
are represented by dashed line
segments. In Figure 12.10(a), for example, one branch (a period-k branch) is
directed toward the bifurcation orbit, one branch (a period-2k branch) is directed
away, and one branch is not directed.
Corollary 12.5 At each generic bifurcation orbit there is one branch
that is directed toward the bifurcation orbit and one branch that is directed away.
516

12.3 GENERIC B IFURCATIONS
k
2k
k
-
S
S
U
-
2k
k
-
S
U
-
S
k
(a) (b)
k k
2k
-
U
+
U
-
S
2k
k
k
-
U
-
U
+
S
(c) (d)
Figure 12.10 Schematic diagrams of the four generic period-doubling bifurca-
tions.
Schematic diagrams of the bifurcations in Figure 12.9 are shown. These bifurcations
are the only generic period-doubling bifurcations for families of one-dimensional
maps or for families of two-dimensional area-contracting maps.
Proof: Lemma 12.4 admits only four possibilities of generic period-
doubling bifurcations, and these are shown in Figure 12.10. Examining these
cases gives the result for period-doubling bifurcations. For saddle-node bifurca-
tions, Exercise 11.8 of Chapter 11 gives generic conditions under which there are
two branches, both on the same side, with oppositely directed arrows, as shown
in Figure 12.7.
✎ E XERCISE T12.5
Use the exchange of stability principle to verify that all the (generic) period-
doubling bifurcations for a family of one-dimensional maps are shown in
Figure 12.10.
In summary, our tinker-toy model for generic one-parameter maps contains
“sockets”, which are saddle-node and period-doubling bifurcations and “sticks”,
which are S branches, U
⫹
branches, or U
⫺
branches. Each schematic branch that
begins or ends within the given parameter range does so at a generic bifurcation
orbit. Figure 12.11 shows a schematic bifurcation diagram illustrating these ideas.
In the next section, we use the theory of schematic diagrams to explain
how chaos develops in one-parameter families of maps.
517

C ASCADES
k
2k
k
k
2k
2k
4k
+
2k
k
4k
16k
8k
+
2k
k
-
-
-
-
-
-
-
-
a
0
a
1
2k
4k
8k
2k
k
k
k
-
Figure 12.11 Schematic model of a bifurcation diagram.
The interconnections of branches of orbits are potentially quite complicated, even
in generic cases. Here we show one such diagram, using only saddle-nodes and
period-doubling bifurcations. Although we have included only a finite number of
bifurcation points, in principle, we could have had period doublings (and even
saddle nodes) of all the periods k, 2k, 4k, 8k,....
12.4 THE CASCADE THEOREM
Poincar
´
e was the first to give a complete mathematical description of a period-
doubling bifurcation, and (Myrberg, 1962) first described a cascade. Cascades
became well known with the applications of (May, 1976). Figures 12.1 and 12.2
show cascades for the one-dimensional quadratic map, and Figure 12.3 shows
cascades for the two-dimensional Poincar
´
e map of the forced damped pendulum.
Many distinct cascades are seen or are hinted at in this picture. Numerical stud-
ies reveal that cascades occur not in isolation but in great profusion, sprinkled
throughout chaotic regimes.
518

12.4 THE C ASCADE T HEOREM
The purpose of this section is to give an explanation of why cascades occur,
and why they must occur in great profusion. The explanation is adequate only
for chaotic systems that have at most one unstable direction at each point (at
most one positive Lyapunov exponent). Indeed there seems to be no reason
to expect to find many cascades in highly chaotic systems that are unstable in
more than one direction. As an example of a class of systems with at most one
positive Lyapunov exponent, we described two-dimensional dissipative systems
in Chapter 11. A dissipative map satisfies | det Df| ⱕ b ⬍ 1, so that the two
Lyapunov numbers of each trajectory satisfy L
1
L
2
ⱕ b. The H
´
enon map (for
fixed |b| ⬍ 1) and the Poincar
´
e map of the forced, damped pendulum are two
examples of dissipative systems with constant Jacobian determinants. In these
cases, L
1
(x)L
2
(x) ⫽ |det Df|, for each initial point x. Although other settings
may satisfy the restriction that there be at most one unstable direction at each
point, the primary applications of the Cascade Theorem will be to families of
one-dimensional maps and families of two-dimensional dissipative systems.
The description is given in terms of a process of orbit creation followed by
stability shedding and builds on two well-known phenomena: the coexistence of
huge numbers of unstable periodic orbits in a chaotic attractor (for a fixed param-
eter value), and the general bifurcation phenomenon known as “the exchange
of stabilities” (Lemma 12.4). As the parameter is increased, the collection of
periodic orbits changes. For example, it might change from a single stable orbit
at parameter value a
0
to the infinite hoard of unstable orbits one expects in a
chaotic attractor at a
c
. We will argue here that the only way in which these
unstable orbits can arise (given the absence of stable orbits at a
c
) is through the
process of cascade formation. Close to half the orbits in a typical chaotic attractor
are regular unstable (U
⫹
) orbits. (See Exercise 12.4.) We will show that for each
of these U
⫹
orbits there must be a distinct cascade occuring in some parameter
range. Therefore, in changing from a single stable periodic orbit to a chaotic
attractor, the system must have had not just one cascade but, in fact, infinitely
many cascades.
We will assume throughout the remainder of this section that f is generic.
While genericity is not a necessary assumption for the result we prove, it does
significantly simplify the arguments. Any map that is not generic can be approx-
imated by a generic map f. The approximation techniques needed to extend our
arguments to the case without genericity assumptions can be found in (Yorke and
Alligood, 1985).
Recall that all orbits on a branch (as shown in Figure 12.4) are the same
type: either all stable S, all regular unstable U
⫹
, or all flip unstable U
⫺
. These
branches end at bifurcation orbits, and the bifurcation orbits serve to connect the
519
