Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

S TAT E R ECONSTRUCTION FROM DATA

of distinguishing between the upswings through 800 and downswings through

800, since they represent two different states of the system. The secret is to make

use of delay coordinates. Instead of trying to represent the state by S(t) alone,

use the pair (S(t),S(t ⫺ 0.03)). If we use the current velocity S(2) ⫽ 800 and

the time-delayed velocity S(1.97) ⫽ 1290 to identify the state at t ⫽ 2, we can

identify the point as in a downswing. On the other hand, for t ⫽ 1.8, the pair

(S(1.8),S(1.77)) ⫽ (825, 560), which we identify as an upswing through 800.

The two different states corresponding to S(t) ⫽ 800 are separately identiﬁed by

the delay plot in Figure 13.1(b).

Figure 13.2 shows how to predict the future. Starting at t ⫽ 2, we collect

analogues from the past, by which we mean states of form (S(t),S(t ⫺ 0.03)) ⫽

(800, 1290), and ﬁnd out what happened to the system 0.5 time units later. For

example, the time series reveals that (S(1.1),S(1.07)) ⫽ (808, 1294), and that

0.5 time units later, the velocity is S(1.6) ⫽ 2125. Also, (S(1.4),S(1.37)) ⫽

(826, 1309) and the future velocity is S(1.9) ⫽ 2123. On the basis of this data we

might predict that S(2.5) ⬇ 2124, the average of the two. The two analogues and

the resulting prediction at t ⫽ 2.5 are shown in Figure 13.2. The prediction does

a fairly good job of matching the actual velocity (shown in the dashed curve) at

t ⫽ 2.5.

If the problem is to predict the velocity at some future time, the delay plot

contains all information we need. If we know S

and S

t⫺T

, we can locate our

current position on the curve. Using past observations, we can accurately predict

800

1600

2400

1 1.5 2 2.5

Velocity

time

prediction

Figure 13.2 Prediction of the future by the method of analogues.

The vertical arrows at t ⫽ 1. 1and1. 4 show two past analogues for the Couette-

Taylor system state at t ⫽ 2. In order to predict the velocity at t ⫽ 2.5, one can use

the future evolution of the system encountered by the analogues (the horizontal

arrows at t ⫽ 1.6and1.9) to predict that the velocity at t ⫽ 2.5 should be about

2124.

540

13.2 DELAY C OORDINATES

where on the curve the system will be in one additional second. We locate the

points on the time series history (on the left of Figure 13.1) which correspond to

points near (S

t⫺T

) in the delay plot (on the right), and mark off the appropriate

amount of time along the time series. If the system is deterministic, meaning that

similar states result in similar outcomes, we will end up with several nearly equal

predictions. In practice, we can average the predictions to improve the statistical

quality of our ﬁnal prediction, if that were our goal.

✎ E XERCISE T13.1

Let x(t) be the height at time t of a falling projectile (it obeys the law

x ⫽⫺g).

Decide whether it is always possible to predict x (2) from the knowledge of

x(0) and x(1) alone. Does the pair [x(0),x(1)] uniquely determine the state

of the projectile?

13.2 DELAY COORDINATES

Periodic orbits move through a one-dimensional set of states. The concept of

dimension is important for quantifying the complexity of a process. The periodic

Couette-Taylor process enters into inﬁnitely many different states, but all states

lie on a one-dimensional curve in the delay plot. In this motion, the system is

restricted to a one-dimensional subset of its (possibly high-dimensional) state

space.

Using the delay coordinates [S(t),S(t ⫺ 0.03)], we were able to remove the

self-intersections of the periodic Couette-Taylor attractor. However, the concept

of delay coordinates is not limited to two-dimensional plots. In general, we can

make the m-dimensional delay plot by graphing the vector of delay coordinates

[S(t),S(t ⫺ T),S(t ⫺ 2T),...,S(t ⫺ (m ⫺ 1)T)]

for each time t in the time series. Attractors that are substantially more compli-

cated than simple closed curves will require more dimensions to be untangled.

Figure 13.3 shows a second example of a periodic orbit. The time series is the

measurement of the electrical impedance across the dorsal vessel, or what passes

for a heart, of a living insect. The heart of Periplaneta americana, the American

cockroach, is a slender pulsatile organ that extends as a long tube from the brain

down the entire body. Electrodes are placed on either side of the tube, about 2

mm apart, and changes in impedance to radio frequencies are recorded which

541

S TAT E R ECONSTRUCTION FROM DATA

-2

-1

0 10 20 30 40

Impedance

time (sec.)

-2

-1

-2 -1 0 1 2

I(t-T)

I(t)

(a) (b)

I(t)

I(t-T)

I(t-2T)

(c)

Figure 13.3 Cockroach heartbeat data.

(a) Time series of impedances tracks 26 beats. (b) Delay plot of series in (a) cannot

be untangled in two dimensions. Time delay is T ⫽ 1 12 sec. (c) Three-dimensional

delay plot shows successful embedding of the attractor and projection to the hori-

zontal plane, which is the same as (b).

mirror the pumping of hemolymph from the abdomen into the head of the insect.

This data set comes from the laboratory of G. Birchard.

Although periodic motion is again evident for this system, there are two ma-

jor differences between this time series and the series from the periodic Couette-

Taylor experiment. First, the heartbeat is much noisier. By noisier, we don’t mean

in the auditory sense, but in the sense of experimental uncertainty. This is reﬂected

both in the non-uniformity of peak heights and troughs in Figure 13.3(a), and in

the extra width of the reconstructed cycle of Figure 13.3(b). The noise is char-

acteristic of all real world processes. The cockroach heart, while simple as organs

go, is a complicated multicellular system, and is not in a precisely periodic orbit.

Furthermore, the electrodes measuring the impedance may be wobbling ever so

542

13.2 DELAY C OORDINATES

slightly, measuring the impedance at slightly different points as time progresses.

Experimental uncertainties like these also affect the Couette-Taylor experiment,

but are much easier to minimize using careful experimental technique than in a

living organism. All things considered, periodicity is still a good description for

the cockroach heartbeat.

✎ E XERCISE T13.2

Assume that S(t) is a periodic time series that has two local maxima per

period, as shown for example in Figure 13.3(a). Show that for some values

of T smaller than the period of S, the delay plot (S(t),S(t ⫺ T)) has a self-

intersection.

The second difference from periodic Couette-Taylor is the crossing point

in Figure 13.3(b). The point at approximately P ⫽ (⫺2 3, ⫺1 3) is a point

of self-intersection of the reconstruction plot. Our method of prediction via

analogues fails at this point, since the knowledge that the current pair of delay

coordinates (I(t),I(t ⫺ T)) is P could mean either of two different states of the

original system. Another measurement is needed to fully untangle the attractor.

The three-dimensional plot of (I(t),I(t ⫺ T),I(t ⫺ 2T)) in Figure 13.3(c) shows

that it is possible to represent the curve in three dimensions without self-crossings.

A one-to-one continuous function from a compact set to ⺢

is called an

embedding of the set, or sometimes a topological embedding, to distinguish it

from other types. The number m is called the embedding dimension of the set.

In Figure 13.1, the periodic orbit of states in the unseen state space is embedded

in ⺢

; the embedding dimension is 2. In Figure 13.3, the periodic orbit fails to

embed in ⺢

(because two points are mapped to the same point), but is embedded

in ⺢

using three delay coordinates.

The achievement of a delay-coordinate embedding is the holy grail of

dynamic data analysis, for the one-to-one property means that every state in

the state space of the system can be uniquely represented by the measured data.

A remarkable theorem says that a ﬁnite-dimensional attractor can always be

embedded in some ⺢

; in fact, the necessary embedding dimension m need be

only a little larger than twice the dimension of the attractor.

To develop some intuition about this fact, we return to our example of a

periodic orbit. Can we expect one-dimensional curves to be embedded in ⺢

The answer is yes, if by “expect” we mean what usually occurs. Figure 13.4 shows

the basic intuition. A closed curve can have a self-intersection, as in (a), in either

⺢

or ⺢

. The difference is that a small bump will dislodge the intersection in ⺢

543

S TAT E R ECONSTRUCTION FROM DATA

(a) (b)

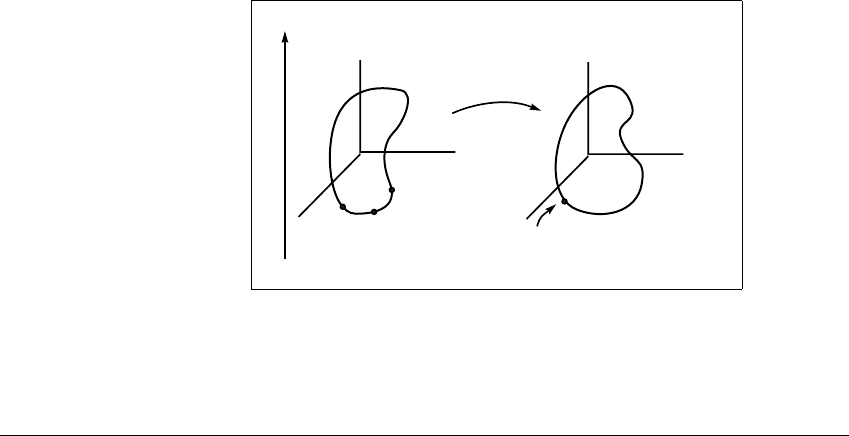
Figure 13.4 Self-intersection of a curve.

(a) The image of a one-dimensional curve by a function to the plane may have

a self-intersection that cannot be removed by small perturbations of the function.

(b) For a function to three dimensional space, small perturbations remove the

self-intersection.

while in ⺢

it will only move the intersection somewhere else. This is a key point.

If the curve represents the series of states of a dynamical system, reconstructed

from measurements, then a slight perturbation in the system dynamics or the

measurement would “typically”, or “generically”, cause the self-intersection in ⺢

to disappear. Although it is certainly possible for curves to have self-intersections

in ⺢

for k ⱖ 3, we should view them as exceptional cases and expect them to

occur with essentially zero probability.

-2000

2000

4000

6000

0 2 4 6 8

Velocity

time

-2000

2000

4000

6000

-2000 0 2000 4000 6000

S(t-T)

S(t)

(a) (b)

Figure 13.5 Chaotic Couette-Taylor experiment.

(a) Time series of velocities from the experiment. (b) Delay plot of data from (a).

544

13.3 EMBEDOLOGY

The set of mathematical facts that underlie this point is investigated in

Challenge 13. There we ﬁnd that two sets of box-counting dimensions d

and d

sitting within ⺢

typically fail to intersect if d

⫹ d

⬍ m. If we imagine for a

moment that the two strands of the curve in Figure 13.4 are separate manifolds,

then they should generically fail to intersect if 1 ⫹ 1 ⬍ m.Ifm ⫽ 3, there should

be no intersection.

If all motion were periodic, and all attractors were curves, the story would

be ﬁnished. Attractors could be generically embedded in three dimensional delay

plots. However, we already know that attractors can have higher dimension.

Moreover, they can be fractals. Figure 13.5 shows a time series of measurements

from the Couette-Taylor experiment when it is in chaotic motion. Can we embed,

examine, and exploit this chaotic attractor as we did the periodic attractor?

13.3 EMBEDOLOGY

It is time to be clearer about the connections between state space, the measure-

ments that comprise a time series, and the reconstructed state space. First suppose

that ⺢

is the state space of a dynamical system, and trajectories are attracted to a

d-dimensional manifold A. Assume that we have a way of making m simultaneous

independent measurements of the system at any given time—not just one, as in a

time series. For each state, then, our measurements yield a vector in ⺢

. We make

the measurements at several different instants, thereby collecting several points

in ⺢

, each one representing m simultaneous measurements. We think of the

measuring process as a function F from ⺢

to ⺢

. At any time, the state is a point

of A in ⺢

, and we can evaluate F at that point by doing the m measurements and

making a vector out of them. The next theorem says that we should expect F(A)

to uniquely represent all states that were in the original manifold A. The proofs

of this theorem and the others that we present in this Chapter are too difﬁcult to

be presented here. However, Challenge 13 explores the main concepts, and gives

directions for those who want to pursue the proofs.

Theorem 13.1 Assume that A is a d-dimensional manifold in ⺢

.Ifm⬎ 2d

and F : ⺢

→ ⺢

is generic, then F is one-to-one on A.

Thismeansthatifx ⫽ y are points on A,thenF(x) ⫽ F(y)in⺢

. Two different

states in A remain different when mapped into ⺢

, or in other words, F(A)has

no self-intersections. Note that Theorem 13.1 does not rule out an embedding

dimension of less than 2d ⫹ 1; it simply guarantees that 2d ⫹ 1 is sufﬁcient in

generic cases. Figure 13.4(b) shows the case d ⫽ 1,m⫽ 3.

545

S TAT E R ECONSTRUCTION FROM DATA

The meaning of generic in Theorem 13.1 was introduced in Chapter 12.

Think of it this way: Even if the image F(A) does have self-intersections, other

functions which are extremely small perturbations of F have no self-intersections.

To be more precise, we can say the following. For any F : ⺢

→ ⺢

,deﬁne

: ⺢

→ ⺢

by F

⫽ F ⫹ M,whereM is the linear map deﬁned by the m ⫻ k

matrix with real entries between ⫺1 and 1. For all but a measure zero set of

choices from the unit cube in ⺢

, the function F

will be one-to-one on A.

Theorem 13.1 is one of the conclusions of the Whitney Embedding Theo-

rem (Whitney, 1936). The statement requires that the coordinates of F are inde-

pendent. Later, it was shown (Takens, 1981) that it is sufﬁcient to choose F from

the special class of functions formed strictly from delay coordinate reconstruc-

tions, using the time series of a single measurement. If we call the measurement

function h : ⺢

→ ⺢, then the delay coordinate function is

F(x) ⬅ [h(x),h(g

⫺T

(x)),...,h(g

⫺(m⫺1)T

(x))].

Here g denotes the dynamical system for which A is the attractor. It can be

either an invertible map, in which g

⫺T

denotes T steps of the inverse map, or a

differential equation, in which case it denotes the state T time units ago. Figure

13.6 is a schematic view of the dynamics g, the scalar measurement function h,

and the delay coordinate function F.

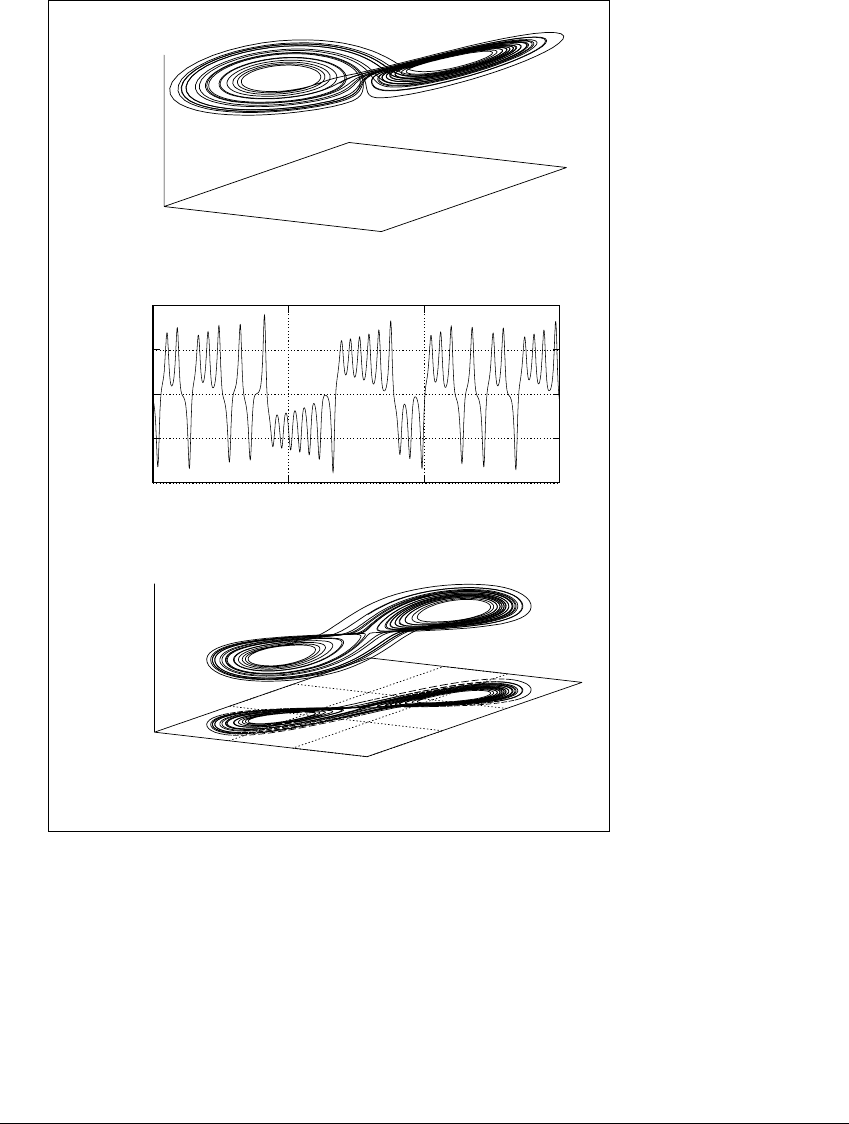
Figure 13.7 shows the result of a delay coordinate reconstruction for the

Lorenz attractor. Figure 13.7(a) is the original state space ⺢

(k ⫽ 3) of xyz-

(v)

F(v) = [h(v),h(g

-T

(v)),h(g

-2T

(v))]

Figure 13.6 Delay coordinate reconstruction function.

With each state v in the state space

⺢

is associated a vector F(v) in reconstruction

space

⺢

. The function h is the measurement function, which is a scalar function

of the state space.

546

13.3 EMBEDOLOGY

(a)

-20

-10

0 10 20 30

x(t)

(b)

x(t)

x(t-T)

x(t-2T)

(c)

Figure 13.7 The Lorenz attractor reconstructed from a time series.

(a) A trajectory from the Lorenz system, 30 time units long. (b) The x-coordinate of

the trajectory in (a) is plotted as a function of t. (c) A delay-coordinate embedding

of the Lorenz attractor, using three delayed values of the time series in (b). The

projection to the ﬁrst two coordinates is also shown. The delay is T ⫽ 0.1.

547

S TAT E R ECONSTRUCTION FROM DATA

variables. The x-coordinate alone is measured and graphed as a time series in (b).

Even though the y and z variables have been thrown away, the three dimensional

graph of [x(t),x(t ⫺ T),x(t ⫺ 2T)] in Figure 13.7(c) gives a fairly faithful visual

reproduction of the original attractor.

Theorem 13.2 Assume that A is a d-dimensional submanifold of ⺢

which

is invariant under the dynamical system g.Ifm⬎ 2dandF : ⺢

→ ⺢

is a delay

coordinate reconstruction function with a generic measurement function h and generic

time delay T, then F is one-to-one on A.

Takens’ Theorem 13.2 says that if the attractor dimension is the integer d,then

for generic delay plots, the embedding dimension is at most 2d ⫹ 1.

✎ E XERCISE T13.3

The genericity requirement on T in Theorem 13.2 is necessary. (a) Show

that if A is a periodic orbit whose period equals the time delay T,thenno

delay coordinate reconstruction function can be one-to-one on A .(b)Show

that the same is true if the period is 2T. [Note: There is no such restriction

for a period 3T orbit.]

Takens’ Theorem 13.2 triggered an avalanche of research, as scientists tried

to interpret time series collected from experiments by drawing delay plots in

enough dimensions to untangle the attractor. In fact, delay coordinate plots were

advocated independently in the physics literature by (Packard et al., 1980). This

technique was one of few available techniques for analyzing potentially chaotic

data. A one-to-one reconstruction means that the method of analogues can be

used to predict short-term future behavior of a system, even in case it is chaotic.

As we already saw in Lab Visit 4, the Couette-Taylor experiment can

exhibit nonperiodic dynamics. Figure 13.5 shows a chaotic Couette-Taylor time

series and reconstructed trajectory. This plot raises the question whether there

is a fact similar to Theorem 13.2 for attractors A which are fractal rather than

manifolds. It turns out that Theorems 13.1 and 13.2 are true for non-manifolds,

as long as the dimension d is interpreted as box-counting dimension.

Theorem 13.3 Assume that A is a subset of ⺢

with box-counting dimension

d. If F : ⺢

→ ⺢

is generic and m ⬎ 2d, then F is one-to-one on A.

Theorem 13.4 Assume that A is a subset of ⺢

with box-counting dimension

d, which is invariant under the dynamical system g.Ifm⬎ 2dandF : ⺢

→ ⺢

548

13.3 EMBEDOLOGY

a delay coordinate reconstruction with a generic measurement function h and a generic

delay T, then F is one-to-one on A.

In Chapter 4 we found the box-counting dimension of the H

enon attractor

of Example 4.11 to be approximately 1.27. Since 2d ⬇ 2.54, we expect the

attractor to be embedded in three dimensions, but not necessarily in two. We test

this conclusion in Figure 13.8. Deﬁne a “measurement” function on the xy state

space of the H

enon map by H(x, y) ⫽ y ⫺ 3sin(x ⫹ y). Figure 13.8 should be read

in the order (b) → (a) → (c). After each (x, y) point is produced on the attractor

in (b), the value of H is plotted in the times series (a). Then a delay map in

the image attractor in (c), corresponding to the fact that the assumption m ⬎ 2d

is not satisﬁed. In (d), a three-dimensional reconstruction, the image does not

cross itself. For this example, the attractor dimension is 1.27, and the embedding

dimension is 3.

✎ E XERCISE T13.4

A set with a small box-counting dimension need not lie in a Euclidean

space of low dimension. For each m ⬎ 1, ﬁnd a subset A of ⺢

such that

boxdim(A) ⬍ 1, but A does not lie in a smooth surface of dimension less

than m. [Hint: Find a subset B of ⺢

such that boxdim(B) ⬍ 1 m.Thenlet

A ⫽ 兵 (x

,...,x

):x

in B, i ⫽ 1,...,m其.]

The Belousov-Zhabotinskii reaction, the subject of Lab Visit 3, was one of

the ﬁrst real experiments to be subjected to delay coordinate reconstruction as

an analysis tool. Figure 13.9(a) shows a time series of the measured bromide ion

concentration from a ﬁxed spot in the reaction apparatus. The time series shows

a certain amount of structure, but it is clearly aperiodic.

Two- and three-dimensional reconstructions of the BZ attractor from the

time series are shown in Figure 13.9(b) and (c). The embedding dimension

appears to be three, using delay T ⫽ 0.05. In panels (d), (e), and (f) of Figure

13.9 the effect of changing the time delay T is explored. As T is varied, one gets

geometrically different but topologically equivalent fractal sets.

For relatively large T ⫽ 0.4, as in panel (f), the reconstructed set begins to

resemble spaghetti. For experimentally measured data from chaotic systems such

as the Belousov-Zhabotinskii reaction, there is a practical upper limit on the time

delay T. Since nearby states are diverging exponentially in time, an experimental

error eventually grows to be comparable to the size of the attractor. If this can

549