Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

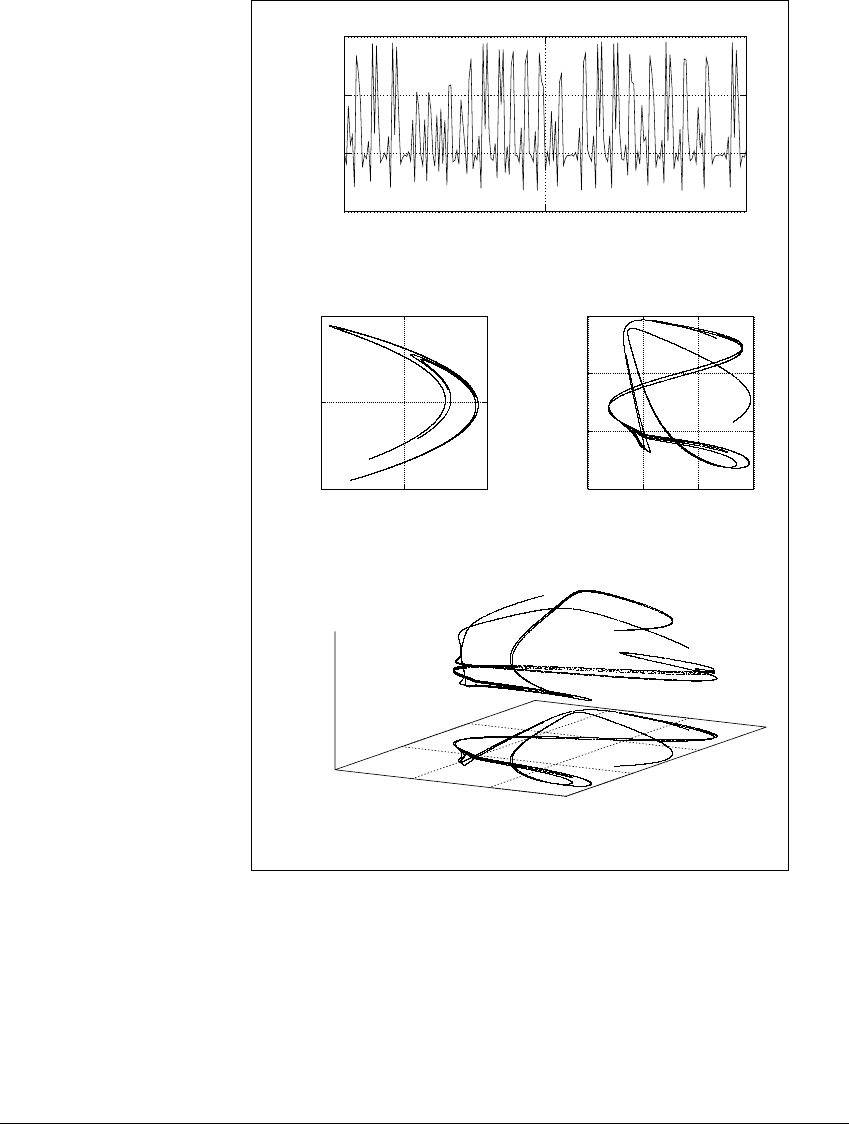
S TAT E R ECONSTRUCTION FROM DATA

-4

-2

0 100 200

h(i)

(a)

-2

-2 0 2

-4

-2

-4 -2 0 2

h(i-1)

h(i)

(b) (c)

h(i)

h(i-1)

h(i-2)

(d)

Figure 13.8 H

enon attractor reconstructed from a time series.

(a) A time series of the function h(i) ⫽ y

⫺ 3 sin(x

⫹ y

), where x

and y

are taken

from the H

enon attractor in (b). (c) A two-dimensional delay reconstruction of the

attractor. (d) A three-dimensional reconstruction. The projection of this set onto

the horizontal plane is seen in (c).

550

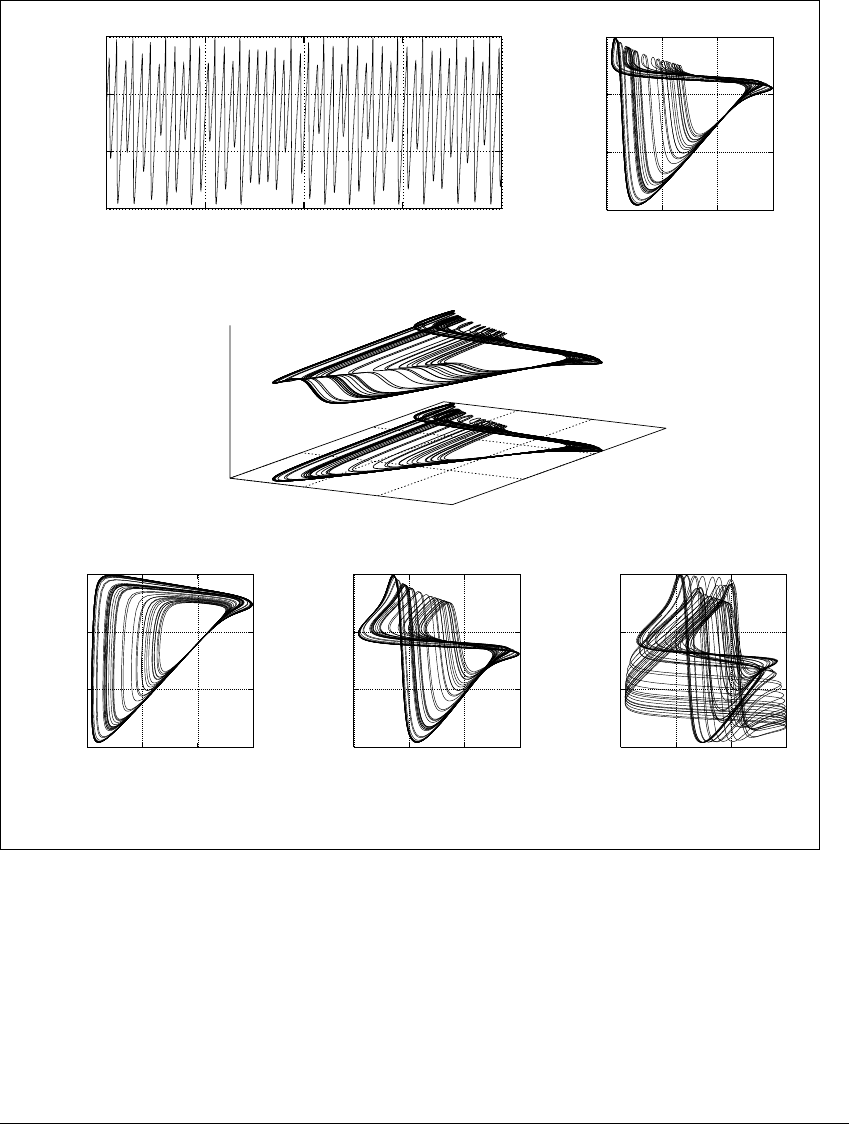
13.3 EMBEDOLOGY

1.4

1.6

1.8

0 3 6 9 12

Br+ concen.

time

1.4

1.6

1.8

1.4 1.6 1.8 2

B(t-T)

B(t)

(a) (b)

B(t)

B(t-T)

B(t-2T)

(c)

1.4

1.6

1.8

1.4 1.6 1.8 2

B(t-T)

B(t)

1.4

1.6

1.8

1.4 1.6 1.8 2

B(t-T)

B(t)

1.4

1.6

1.8

1.4 1.6 1.8 2

B(t-T)

B(t)

(d) (e) (f)

Figure 13.9 Belousov-Zhabotinskii reaction data.

(a) Time series of bromide ion concentration, provided by Anke Brandstater.

(b) Two-dimensional delay reconstruction of the BZ attractor, with time delay

T ⫽ 0.05. (c) Three-dimensional reconstruction whose projection is (b). The re-

maining three panels show delay plots with three different choices of delay time T.

(d) T ⫽ 0.02 (e) T ⫽ 0.1(f)T ⫽ 0.4

551

S TAT E R ECONSTRUCTION FROM DATA

happen during the time spanned by a single delay coordinate vector, the state

that the vector speciﬁes will have limited value for applications like prediction.

Entire books have been written about state reconstruction from data and

the scientiﬁc applications that follow. Ott, Sauer, and Yorke, 1994 is a starting

point for further exploration.

552

C HALLENGE 13

☞ C HALLENGE 13

Box-Counting Dimension and Intersection

OW LARGE does a space have to be so that two sets can move around

and generally avoid one another? The x-axis and y-axis of the plane intersect at

the origin. If we move either or both of them slightly, they still intersect, at a

point somewhere near the origin. But if we add another dimension, they hardly

ever intersect. The x and y axes in ⺢

intersect at the origin, but a small push of

either one in almost any direction (except a push precisely along the xy-plane)

eliminates the intersection.

In Challenge 13 we want to explore and eventually prove the fact that two

sets of dimension d

and d

sitting in ⺢

usually don’t intersect if d

⫹ d

⬍ m.By

dimension, we mean box-counting dimension. There are interesting applications

of this fact for fractal sets. By “usually”, we mean that intersections are possible

but that they are unusual cases in some sense—a little push, or spatial translation,

causes the intersections to disappear. The x and y axes have dimensions d

⫽ 1

and d

⫽ 1, so d

⫹ d

⫽ 2. Two lines in a Euclidean space of dimension three or

more should intersect only if they are placed just so.

Certainly we can make any two nonempty sets intersect by moving them

so that they have a point in common. If the intersection is robust, the sets should

still intersect if they are moved a small amount. This is the situation for two lines

in the plane, but not for two lines in ⺢

What do we mean by moving the sets? We could allow many kinds of

rigid motions, that change the location of the set without changing the relative

positions of the points in the set. To keep things simple, let’s restrict our movement

to spatial translations, which are the result of vector addition of a single point to

each of the sets. Adding the vector (1, 1) to a set in the plane moves the set one

unit up and one unit to the right. We might as well let one of the two sets stay

ﬁxed and move the other, to simplify matters.

Let S be a subset of ⺢

,andletv be a point in ⺢

. We will call the set

S ⫹ v ⫽ 兵s ⫹ v : s in S其 the translation of the set S by v. The translated set is

found by adding v to each point in S, in other words, moving S rigidly to a

new location speciﬁed by v. For two subsets S

and S

of ⺢

,wewillsaythatthe

translates of S

almost never intersect S

if the set 兵v in ⺢

:(S

⫹ v) 傽 S

⫽⭋其

has m-dimensional volume zero. This deﬁnition is symmetric in S

and S

;itis

553

S TAT E R ECONSTRUCTION FROM DATA

equivalent that the translates of S

almost never intersect S

. We can now restate

our goal in these more precise terms:

Theorem 13.5 Let S

and S

be subsets of ⺢

of box-counting dimensions d

and d

, respectively. If d

⫹ d

⬍ m, then the translates of S

almost never intersect

In this sense, the x and y axes always intersect in ⺢

, but almost never

intersect in ⺢

. To see the latter, notice that of all possible translations in ⺢

only those of form v ⫽ (x, y, 0) preserve the intersection. This exceptional set

of translations corresponds to the xy-plane, which is a set of three-dimensional

volume 0.

Challenge 13 has three parts. The ﬁrst two concern self-intersection inside

the real line, which refers to the case S

⫽ S

and m ⫽ 1. The Cantor middle-

third set has dimension greater than 1 2, so the Theorem does not apply. In

fact, you will show that every translation of the Cantor set S

⫹ v intersects

the (untranslated) Cantor set S

, provided ⫺1 ⬍ v ⬍ 1. Second, we consider the

middle three-ﬁfths Cantor set, which has dimension less than 1 2. A pair of these

sets almost never intersect under translation, which is consistent with Theorem

13.5. Finally, you will put together a proof of the theorem.

We learned earlier that the box-counting dimension of the middle-third

Cantor set S is ln 2 ln 3 ⬇ 0.63. Because 2 ⫻ 0.63 ⬎ 1, we do not expect two

translated middle-third Cantor sets to be able to avoid one another within the

real line. In fact, Step 3 shows that for any 0 ⬍ v ⬍ 1, the translated Cantor

set S ⫹ v has a point in common with the Cantor set S. Recall that in base 3

arithmetic, the middle-third Cantor set consists of all expansions that can be

made using only the digits 0 and 2.

Step 1 Explain the fact that if x is in the middle-third Cantor set, then so

is 1 ⫺ x.

Step 2 Show that if x is in [0, 1], then x can be written as the sum of two

base 3 expansions each of which use only the digits 0 and 1.

Step 3 Let v be any number in [0, 1]. Then (v ⫹ 1) 2isalsoin[0, 1]. Use

Step 2 to show that v ⫹ 1 is the sum of two numbers belonging to the middle-third

Cantor set S. Use Step 1 to conclude that there is a number in S which when

added to v gives another number in S. Therefore for each number v in [0, 1], the

set S ⫹ v intersects with S.

The next three steps refer to the middle-3/5 Cantor set K(5). This set is

analogous to the middle-third Cantor set, except that we remove the middle 3 5

554

C HALLENGE 13

.00

1/5

4/5

.44

.40

.04

1/25

4/25

21/25

24/25

1/5

4/5

Figure 13.10 The middle three-ﬁfths Cantor set construction.

At each step, the middle three-ﬁfths of each remaining interval is removed. This

Cantor set contains all numbers whose base 5 expansion can be made with only

the digits 0 and 4. The set denoted .04 consists of all numbers in the interval [0, 1]

whose expansion begins with .04.

of each remaining interval instead of the middle one-third. See Figure 13.10 for

a schematic view of the construction.

Step 4 Verify that the middle-3/5 Cantor set consists of all numbers in

[0, 1] possessing a base 5 expansion containing only the digits 0 and 4. Find the

box-counting dimension of K(5). Show that if S

and S

are both the middle-3/5

Cantor set, then the dimensions satisfy d

⫹ d

⬍ 1.

Step 5 Let v be a number in [0, 1] whose base 5 expansion contains a 22

(two adjacent base 5 digits are 2). Show that S

⫹ v does not intersect S

Step 6 Show that the set of numbers whose base 5 expansion does not

contain a 22 is a length 0 set. Conclude that translates of the middle-3/5 Cantor

set almost never intersects itself. [Hint: Sketch the subinterval .22, which consists

of 1 25 of the interval [0, 1]. Each of the remaining subintervals .s

of length

1 25 have a subinterval .s

22, and so on. Sum up the lengths.]

Next you will prove Theorem 13.5. Assume that S

and S

are bounded

subsets of ⺢

of box-counting dimensions d

and d

, respectively. Put down an

⑀

-grid over ⺢

for some

⑀

⬎ 0. Consider two

⑀

-cubes, one containing points of

and the other containing points of S

. To begin, Step 7 asks you to ﬁnd out

how likely it is for the two cubes to intersect under translation.

555

S TAT E R ECONSTRUCTION FROM DATA

Step 7 Let C

and C

be m-dimensional cubes of side

⑀

chosen from the

grid in ⺢

. Show that the subset of points v such that the translation C

⫹ v

intersects C

is less than C

⑀

, for some constant C.[Hint:DenotebyP

and P

the centers of the cubes. The cubes can’t intersect unless the distance between

⫹ v and P

is less than



⑀

. Show that the cubes don’t intersect as long as v

avoids the ball of radius



⑀

centered at P

⫺ P

Step 8 Let N

(

⑀

) be the number of

⑀

-cubes covering S

,andN

(

⑀

)bethe

number covering S

. The number of pairs of

⑀

-cubes, one from S

and one from

,isN

(

⑀

(

⑀

). Denote by B

(r) the set of points in ⺢

within a distance r

of the origin. Use Step 7 to conclude that the subset of B

(r) corresponding to

vectors v that cause any of these pairs to collide under translation by v has volume

at most CN

(

⑀

(

⑀

)

⑀

,whereC is a constant.

Step 9 Use the deﬁnition of box-counting dimension and the assumption

that d

⫹ d

⬍ m to prove that the volume in Step 8 goes to zero as

⑀

→ 0. Thus

the volume of translating vectors within B

(r) which cause any intersections of

the translated S

with S

is zero. This is true no matter how large r is, so the

translates of S

almost never intersect S

Postscript. Theorem 13.5 and its proof in Step 9 are closely related to Theorems

13.3 and 13.4. To achieve the embedding in Theorem 13.3 it is necessary for the images

of distant sections of the attractor in state space to almost always miss each other in

reconstruction space

⺢

. It can be shown that small linear perturbations of the function

F :

⺢

→ ⺢

in Theorem 13.3 have a similar effect as rigid translations in Theorem 13.5.

Since the distant sections each have box-counting dimension d, the necessary condition

of Theorem 13.5 amounts to 2d ⬍ m in the notation of Theorem 13.3. Theorem 13.4

follows from showing that small perturbations of the scalar measurement function h alone

are sufﬁcient to restrict self-intersections to occur with probability zero. See (Sauer, Yorke,

and Casdagli, 1991) for full details.

556

A PPENDIX A

Matrix Algebra

N THIS APPENDIX we review important concepts from matrix algebra.

A.1 EIGENVALUES AND EIGENVECTORS

Deﬁnition A.1 Let A be an m ⫻ m matrix and x a nonzero m-dimensional

real or complex vector. If Ax ⫽

␭

x for some real or complex number

␭

,then

␭

called an eigenvalue of A and x the corresponding eigenvector.

For example, the matrix A ⫽





has an eigenvector





,andcor-

responding eigenvalue 4.

557

M ATRIX A LGEBRA

Eigenvalues are found as roots

␭

of the characteristic polynomial det(A ⫺

␭

I). If

␭

is an eigenvalue of A, then any nonzero vector in the nullspace of A ⫺

␭

is an eigenvector corresponding to

␭

. For this example,

det(A ⫺

␭

I) ⫽ det



1 ⫺

␭

22⫺

␭



⫽ (

␭

⫺ 1)(

␭

⫺ 2) ⫺ 6

⫽ (

␭

⫺ 4)(

␭

⫹ 1), (A.1)

so the eigenvalues are

␭

⫽ 4, ⫺1. The eigenvectors corresponding to

␭

⫽ 4are

found in the nullspace of

A ⫺ 4I ⫽



⫺33

2 ⫺2



(A.2)

and so consist of all nonzero multiples of





. Similarly, the eigenvectors corre-

sponding to

␭

⫽⫺1 are all nonzero multiples of



⫺2



If A and B are m ⫻ m matrices, then the set of eigenvalues of the product

matrix AB is the same as the set of eigenvalues of the product BA. In fact, let

␭

be an eigenvalue of AB,sothatABx ⫽

␭

x for some x ⫽ 0.If

␭

⫽ 0, then

0 ⫽ det(AB ⫺

␭

I) ⫽ det(AB) ⫽ (det A)(det B) ⫽ det(BA ⫺

␭

I),

␭

⫽ 0 is also an eigenvalue of BA.If

␭

⫽ 0, then ABx ⫽

␭

x implies BA(Bx) ⫽

␭

Bx.NotethatBx ⫽ 0 because

␭

⫽ 0andx ⫽ 0. Therefore Bx is an eigenvector

of the matrix BA with eigenvalue

␭

A generalization of this fact is Lemma A.2.

Lemma A.2 If A

,...,A

are m ⫻ m matrices, then A

⭈⭈⭈A

and the

cyclic permutation A

r⫹1

⭈⭈⭈A

have the same set of eigenvalues, where

1 ⱕ r ⱕ n.

This follows from the previous paragraph by setting A ⫽ A

⭈⭈⭈A

and B ⫽

r⫹1

⭈⭈⭈A

Deﬁnition A.3 The m ⫻ m matrices A

and A

are similar, denoted

⬃ A

, if there exists an invertible m ⫻ m matrix S such that A

⫽ SA

⫺1

Similar matrices have identical eigenvalues, because their characteristic

polynomials are identical:

⫺

␭

I ⫽ SA

⫺1

⫺

␭

I ⫽ S(A

⫺

␭

I)S

⫺1

(A.3)

558

A.1 EIGENVALUES AND E IGENVECTORS

implies that

det(A

⫺

␭

I) ⫽ (det S) det(A

⫺

␭

I)detS

⫺1

⫽ det(A

⫺

␭

I). (A.4)

If a matrix A has eigenvectors that form a basis for R

,thenA is similar to

a diagonal matrix, and A is called diagonalizable. In fact, assume Ax

⫽

␭

for

i ⫽ 1,...,m, and deﬁne the matrix

S ⫽







⭈⭈⭈ x







Then one can check that the matrix equation

AS ⫽ S







␭







(A.5)

holds. The matrix S is invertible because its columns span R

. Therefore A is

similar to the diagonal matrix containing its eigenvalues.

Not all matrices are diagonalizable, even in the 2 ⫻ 2 case. In fact, all 2 ⫻ 2

matrices are similar to one of the following three types:

1. A

⫽



a 0

0 b



2. A

⫽



a 1

0 a



3. A

⫽



a ⫺b



Remember that eigenvalues are identical for similar matrices. A matrix is similar

to case 1 if there are two eigenvectors that span ⺢

; a matrix is similar to case 2 if

there is a repeated eigenvalue with only one dimensional space of eigenvectors;

and to case 3 if it has a complex pair of eigenvalues.

The proof of the fact that the three types sufﬁce for 2 ⫻ 2 matrices fol-

lows from the Cayley-Hamilton Theorem, which states that a matrix satisﬁes its

characteristic equation.

Theorem A.4 (Cayley-Hamilton) If P(

␭

) is the characteristic polynomial of

the matrix A, then P(A) ⫽ 0 (as a matrix equation).

559