Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

B IFURCATIONS

If all the multipliers of

␥

are inside (respectively, outside) the unit circle in

the complex plane, then

␥

is called an attracting (respectively, repelling) periodic

orbit. If

␥

has some multipliers inside and some multipliers outside the unit circle,

then

␥

is called a saddle periodic orbit.

Finding multipliers of a periodic orbit is largely accomplished through com-

putational methods, since cases in which a Poincar

e map can be explicitly deter-

mined are rare. One such case follows.

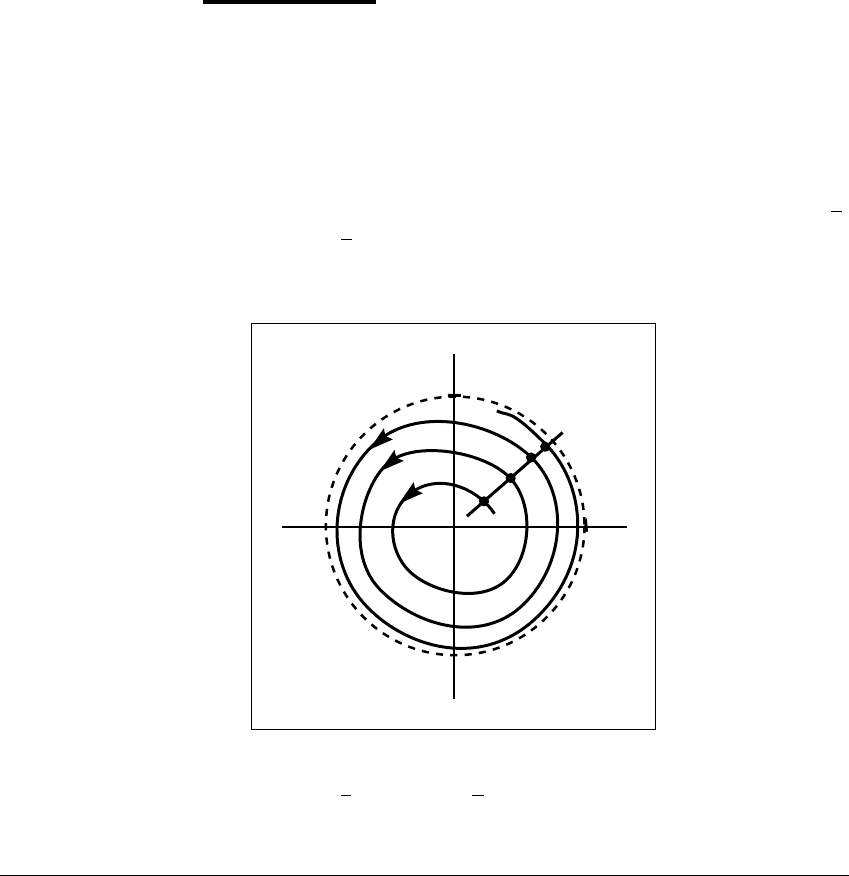
E XAMPLE 11.18

Let

r ⫽ br(1 ⫺ r) (11.10)

␪

⫽ 1

where b is a positive constant, and (r,

␪

) are polar coordinates. Since

r ⫽ 0when

r ⫽ 1, the unit circle r ⫽ 1 is a periodic orbit. A segment L of the ray

␪

⫽

␪

(any ﬁxed angle

␪

will sufﬁce), serves as the domain of a Poincar

e map. Figure

11.20 illustrates one orbit 兵r

,...其 of the Poincar

e map for the limit cycle

Figure 11.20 Poincar

e map for a limit cycle of a planar system.

The system

⫽ 0.2r(1 ⫺ r),

␪

⫽ 1, has a limit cycle r ⫽ 1. The line segment L

is approximately perpendicular to this orbit. Successive images r

,...,of initial

point r

under the Poincar

e map converge to r ⫽ 1.

480

11.7 BIFURCATIONS IN DIFFERENTIAL E QUATIONS

r ⫽ 1 of (11.10) with b ⫽ 0.2. Using the fact that a trajectory returns to the

same angle after 2

␲

time units, we separate variables in (11.10), and integrate a

solution from one crossing, r

, to the next, r

n⫹1

of L:



n⫹1

r(1 ⫺ r)

⫽



␲

bdt ⫽ 2

␲

Evaluating the integral on the left (by partial fractions), we obtain

n⫹1

(1 ⫺ r

)

(1 ⫺ r

n⫹1

)

⫽ e

␲

(a) (b)

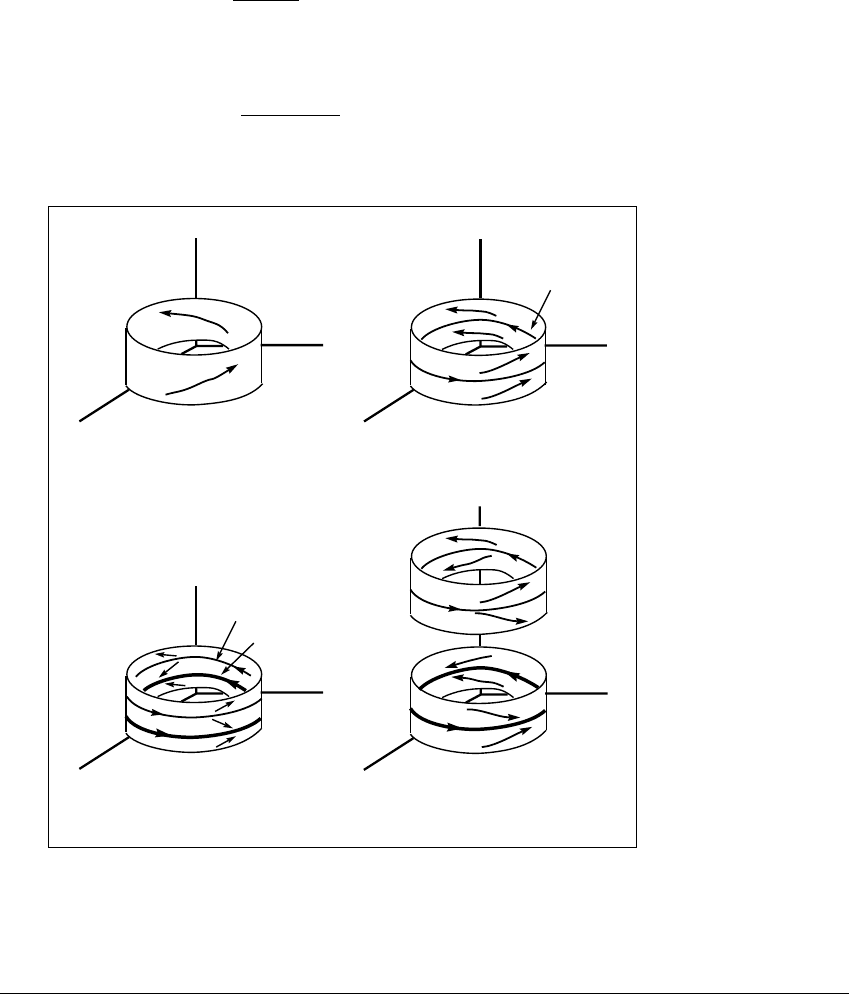
Figure 11.21 A saddle-node bifurcation for a three-dimensional ﬂow.

(a) The system begins with no periodic orbits. (b) The parameter is increased, and

a saddle-node periodic orbit C appears. (c) The saddle-node orbit splits into two

periodic orbits C

and C

, which then move apart, as shown in (d).

481

B IFURCATIONS

Then, solving for r

n⫹1

⫽

␲

1 ⫺ r

⫹ r

␲

. (11.11)

✎ E XERCISE T11.15

(a) Show that for b ⬎ 0, the sequence 兵r

其, as deﬁned by (11.11),

converges to 1 as n →

⬁

(b) Find the Floquet multiplier of the orbit r ⫽ l.

Through the Poincar

e map and time-T map, we can exploit the bifurca-

tion theory developed for maps to study the bifurcations of periodic orbits of

parametrized differential equations. For v 僆⺢

and a scalar parameter a,let

˙v ⫽ f

(v) (11.12)

denote a one-parameter family of differential equations. As before, a periodic orbit

␥

of (11.12) is classiﬁed as “continuable” or a “bifurcation” orbit, depending on

whether v

␥

is a locally continuable or bifurcation orbit for the one-parameter

continuation of the Poincar

emapT or time-T map F

(a) (b)

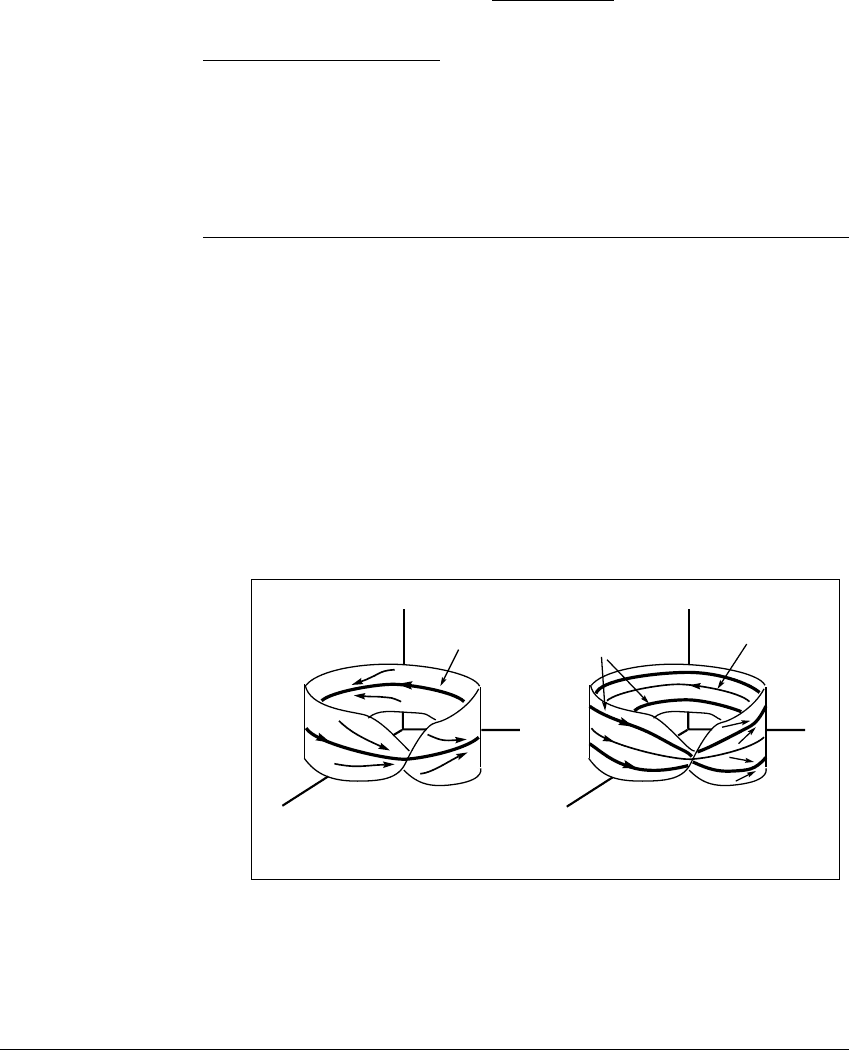
Figure 11.22 A period-doubling bifurcation for a three-dimensional ﬂow.

The system begins with a periodic orbit C

, which has one multiplier between 0

and ⫺1, as shown in (a). As the parameter is increased, this multiplier crosses ⫺1,

and a second orbit C

of roughly twice the period of C

bifurcates. This orbit wraps

twice around the M

obius strip shown in (b).

482

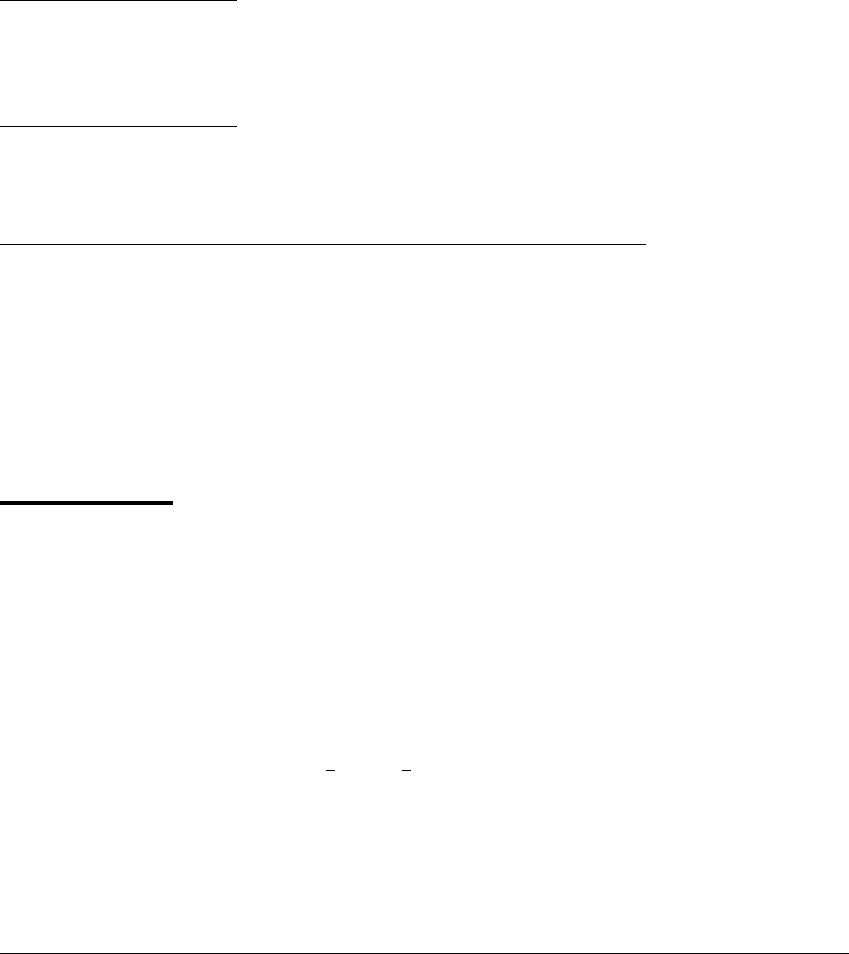
11.8 HOPF B IFURCATIONS

Figure 11.21 shows a saddle-node bifurcation of periodic orbits, and Figure

11.22 shows a period-doubling bifurcation. Recall that at a saddle-node bifurca-

tion orbit, the linearized map has an eigenvalue of ⫹1. In the case of a ﬂow, a

multiplier of the periodic orbit must be ⫹1. For a period-doubling bifurcation,

the orbit must have a multiplier of ⫺1.

✎ E XERCISE T11.16

After a period-doubling bifurcation, are the periodic orbits linked or un-

linked? (See, for example, the orbits C

and C

, as shown in Figure 11.22(b).)

✎ E XERCISE T11.17

Show that a one-parameter family of autonomous plane differential equa-

tions cannot contain any period-doubling bifurcation orbits.

11.8 HOPF BIFURCATIONS

Saddle-node and period-doubling bifurcations are not the only ways in which

periodic orbits are born in one-parameter families. There is one more “generic”

bifurcation. In an Andronov-Hopf bifurcation (often shortened to Hopf bifurca-

tion), a family of periodic orbits bifurcates from a path of equilibria.

E XAMPLE 11.19

(Hopf bifurcation.) Let

x ⫽⫺y ⫹ x(a ⫺ x

⫺ y

)

y ⫽ x ⫹ y(a ⫺ x

⫺ y

) (11.13)

for x, y, and a in ⺢. The bifurcation diagram for this system is illustrated in Figure

11.23. Verify that for a ⬎ 0, there are periodic solutions of the form

(x(t),y(t)) ⫽ (



a cos t,



a sin t).

In polar coordinates, equations (11.13) have the simple form

r ⫽ r(a ⫺ r

)

␪

⫽ 1. (11.14)

483

B IFURCATIONS

(a) (b)

Figure 11.23 Supercritical Hopf bifurcation.

(a) The path 兵(a, 0, 0)其 of equilibria changes stability at a ⫽ 0. A stable equilibrium

for a ⬍ 0 is replaced by a stable periodic orbit for a ⬎ 0. (b) Schematic path diagram

of the bifurcation. Solid curves are stable orbits, dashed curves are unstable.

For each a, the origin r ⫽ 0 is an equilibrium of (11.14). When a is negative,

r is negative, and all solutions decay to 0. For each a ⬎ 0, there is a nontrivial

periodic solution r ⫽



a. A path of periodic orbits bifurcates from v at a ⫽ 0. In

this example, notice that there is exactly one periodic orbit for each planar ﬂow

when a ⬎ 0.

Common to bifurcations we have discussed, the family of periodic orbits

bifurcates from a path of equilibria that changes stability at the bifurcation point.

In this case, the equilibria go from attractors to repellers. We picture this planar

nonlinear case in Figure 11.24. The variation in parameter brings about a small

change in the vector ﬁeld near the equilibrium, causing a change in its stability.

Meanwhile, the vector ﬁeld outside a small neighborhood N of the equilibrium

remains virtually unchanged, with the vector ﬁeld still pointing in towards the

equilibrium. Orbits within N are trapped and, in the absence of any other equi-

libria, must converge to a periodic orbit.

Deﬁnition 11.20 Assume that

v is an equilibrium at a ⫽ a for the one-

parameter family (11.12). We say that a path of periodic orbits bifurcates from

(

a, v) if there is a continuous path of periodic orbits that converge to the equilib-

rium at a ⫽

In order to simplify the discussion here, we assume as in the previous

example that v ⫽ 0 is an equilibrium for all a (that is, f

(0) ⬅ 0 in (11.12)).

484

11.8 HOPF B IFURCATIONS

(a) (b)

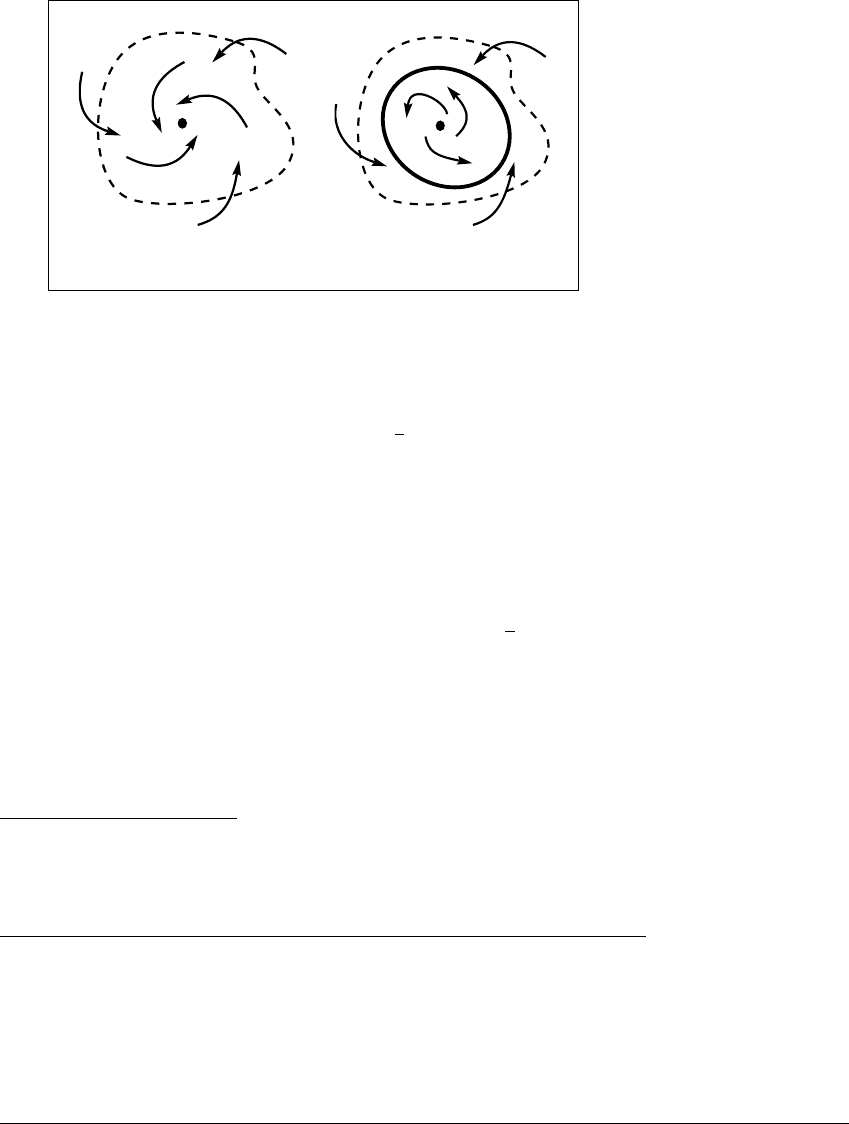
Figure 11.24 A periodic orbit bifurcates from an equilibrium in the plane.

As the equilibrium goes from attracting (a) to repelling (b), a periodic orbit appears.

Also, we assume that the bifurcation occurs at a ⫽ 0. The eigenvalues of the

matrix D

(0) vary continuously with a. We can refer to a path c(a) ⫹ ib(a)of

eigenvalues of the matrix. (In Example 11.19, one checks that c(a) ⫹ ib(a) ⫽

a ⫹ i.) A version of the following theorem was ﬁrst proved by E. Hopf in 1942.

For more details, see (Kocak and Hale, 1991).

Theorem 11.21 (Andronov-Hopf Bifurcation Theorem.) Let ˙v ⫽ f

(v)

be a family of systems of differential equations in ⺢

with equilibrium v ⫽ 0 for all a. Let

c(a) ⫾ ib(a) denote a complex conjugate pair of eigenvalues of the matrix Df

(0) that

crosses the imaginary axis at a nonzero rate at a ⫽ 0; that is, c(0) ⫽ 0,b⫽ b(0) ⫽ 0,

and c



(0) ⫽ 0. Further assume that no other eigenvalue of Df

(0) is an integer multiple

of bi. Then a path of periodic orbits of (11.12) bifurcates from (a, v) ⫽ (0, 0).The

periods of these orbits approach 2

␲

 b as orbits approach (0, 0).

✎ E XERCISE T11.18

Show that the system (11.13) satisﬁes the hypotheses of the Hopf Bifurca-

tion Theorem, and describe the conclusion of the theorem for this system.

Remark 11.22 There is a weaker form of the Hopf Bifurcation Theorem

that is useful for some purposes. The weaker version has a less stringent hypothesis,

and delivers a weaker conclusion. Instead of assuming that the pair of eigenvalues

crosses the imaginary axis with nonzero speed at a ⫽ 0, assume simply that it

crosses the imaginary axis at a ⫽ 0. All other hypotheses remain unchanged.

485

B IFURCATIONS

(For example, the eigenvalues might move as c(a) ⫾ ib(a) ⫽ a

⫾ i.) Then the

conclusion is that every neighborhood of (

a, v) ⫽ (0, 0), no matter how small,

contains a periodic orbit. They may not be parametrized by a continuous path in

the parameter a. See (Alexander and Yorke, 1978).

Hopf bifurcations come in several types, depending on what happens to

orbits near the equilibrium at the bifurcation point. Two types are important

in experimental work, because they explain the important phenomenon of the

creation of periodic behavior. At a supercritical bifurcation, the equilibrium at

the bifurcation value of the parameter, which we might call the bifurcation orbit,

is stable. A supercritical Hopf bifurcation is illustrated in Figure 11.23. When seen

in experiment, a supercritical Hopf bifurcation is seen as a smooth transition. The

formerly stable equilibrium starts to wobble in extremely small oscillations that

grow into a family of stable periodic orbits as the parameter changes.

When the bifurcation orbit is unstable, the bifurcation is called subcritical.

A subcritical Hopf bifurcation, illustrated in Figure 11.25, is seen experimentally

as a sudden jump in behavior. As the parameter a is increased in the ﬁgure,

the system follows the equilibrium v ⫽ 0 until reaching the bifurcation point

a ⫽ 0. When this point is passed, no stable equilibrium exists, and the orbit is

immediately attracted to the only remaining stable orbit, an oscillation of large

amplitude. In this case, the bifurcating path of periodic orbits of the Hopf bifurca-

tion exists for a ⬍ 0. The periodic orbits thrown off from the origin for negative

a are unstable orbits. For a ⬍ 0, they provide a basin boundary between the at-

tracting equilibrium and the attracting periodic orbit on the outside. When this

boundary disappears at a ⫽ 0, immediate changes occur. Lab Visit 11 involves the

interpretation of sudden changes in current oscillations from an electrochemistry

experiment. In this case, the scientists conducting the experiment ﬁnd that a

subcritical Hopf bifurcation is the likely explanation.

An important nonlinear effect often seen in the presence of a subcritical

Hopf bifurcation is hysteresis, which refers to the following somewhat paradoxical

phenomenon. Assume a system is being observed, and shows a particular behavior

at a given parameter setting. Next, the parameter is changed, and then returned

to the original setting, whereupon the system displays a behavior completely

different from the original behavior. This change in system behavior, which

depends on the coexistence of two attractors at the same parameter value, is

called hysteresis.

We have all seen this effect before. If you start with an egg at room tem-

perature, raise its temperature to 100

◦

C. for three minutes, and then return the

egg to room temperature, the state of the egg will have changed. However, you

486

11.8 HOPF B IFURCATIONS

(a) (b)

Figure 11.25 A subcritical Hopf bifurcation with hysteresis.

(a) There is a bifurcation at a ⫽ 0 from the path r ⫽ 0 of equilibria. At this

point the equilibria go from stable to unstable, and a path of unstable periodic

orbits bifurcates. The periodic orbits are unstable and extend back through negative

parameter values, ending in saddle node at a ⫽⫺1. An additional path of attracting

periodic orbits emanates from the saddle node. (b) Schematic diagram of bifurcation

paths. The rectangle shows a hysteretic path. The vertical segments correspond to

sudden jumps.

may not be used to seeing this behavior in a reversible dynamical system such as

a differential equation.

Figure 11.25 shows one way in which a system can undergo hysteresis. If

the system is started at the (attracting) equilibrium at 0 for parameter a ⬍ 0, it

will stay there. When the parameter is increased to a ⬎ 0, the equilibrium at 0

becomes unstable, and any small perturbation will cause the orbit to be attracted

to the outside stable periodic orbit. When the parameter is decreased back to the

starting value a ⬍ 0, the orbit stays on the periodic orbit, unless a large external

perturbation moves it back inside the basin of the equilibrium. Hysteretic effects

can be seen in the data collected in Lab Visit 11.

Figure 11.25 shows the stable and unstable periodic orbits being created

together in a saddle-node bifurcation. If the parameter is decreased to extreme

negative values, beyond the saddle-node point, then the system will of course

return to equilibrium behavior.

487

B IFURCATIONS

E XAMPLE 11.23

A subcritical Hopf bifurcation is seen in the system

r ⫽ ar ⫹ 2r

⫺ r

␪

⫽ 1. (11.15)

The bifurcation diagram of equilibria and periodic orbits of equations (11.15)

is shown in Figure 11.25. There is a subcritical Hopf bifurcation at a ⫽ 0from

the path r ⫽ 0, at which point a path of unstable orbits bifurcates. This path

contains unstable periodic orbits and extends through negative a values, ending

in a saddle node bifurcation at a ⫽⫺1. A path of stable orbits emanates from the

saddle node. Thus for the interval ⫺1 ⬍ a ⬍ 0 of parameter values there are two

attractors: an attracting equilibrium and an attracting periodic orbit.

✎ E XERCISE T11.19

Find all periodic orbits in the system of equations (11.15), and check their

stability. Verify that Figure 11.25 is the bifurcation diagram.

Example 11.19 was our ﬁrst example of a one-parameter family of differential

equations that satisﬁed the hypotheses of the Hopf Bifurcation Theorem. In the

path of periodic orbits that bifurcates from the origin, there is exactly one periodic

orbit for each parameter value when a ⬎ 0. However, the path of bifurcating orbits

need not follow this pattern. In the following example, the entire path of orbits in

(a, v) space exists at only one parameter value, a ⫽ 0. The path must, however,

emanate from v ⫽ 0.

E XAMPLE 11.24

Let

x ⫽ ax ⫹ y

y ⫽ ay ⫺ x (11.16)

for x, y, and a in ⺢ . This one-parameter family of linear differential equations has

a Hopf bifurcation from the path

v ⫽ 0 of equilibria at a ⫽ 0. (Check the path

of eigenvalues to show that they satisfy the hypotheses of Theorem 11.21.) In

this case, however, instead of having one periodic orbit of the bifurcating family

488

11.8 HOPF B IFURCATIONS

at each a ⬎ 0 (or, analogously, a ⬍ 0), the entire family of periodic orbits exists

only at a ⫽ 0.

✎ E XERCISE T11.20

Find all periodic orbits of the one-parameter family (11.16).

E XAMPLE 11.25

(Lorenz Equations) As we discussed in Chapter 9, the system of equations

below was ﬁrst studied by Lorenz and observed to have chaotic attractors. For

(x, y, z)in⺢

, let

⫽

␴

(y ⫺ x) (11.17)

⫽ rx ⫺ y ⫺ xz (11.18)

⫽⫺bz ⫹ xy,

for constant

␴

⬎ 0,r ⬎ 0, and b ⬎ 0.

The origin is an equilibrium for all values of the parameters. For r ⬎ 1, the

points c

⫾

⫽ (⫾



b(r ⫺ 1), ⫾



b(r ⫺ 1),r⫺ 1) are also equilibria. For r ⬍ 1,

the origin is an attractor. For r ⬎ 1, the origin is unstable, while the points c

⫾

are

attracting. The bifurcation at r ⫽ 1 is shown in Figure 11.26 for speciﬁc values of

b and

␴

. There is also a subcritical Hopf bifurcation at r ⫽ r

⫽

␴

(

␴

⫹b⫹3)

␴

⫺b⫺1

.This

value is derived in Exercise 11.21.

✎ E XERCISE T11.21

(a) Show that the degree-three monic polynomial

␭

⫹ a

␭

⫹

␭

⫹ a

has pure imaginary roots if and only if a

⫽ a

and a

⬎ 0. Show

that the roots are

␭

⫽⫺a

and

␭

⫽⫾i



. (b) Evaluate the Jacobian of

the Lorenz vector ﬁeld at the equilibria c

⫾

and show that these equilibria

have pure imaginary eigenvalues

␭

⫽⫾i

␴

(

␴

⫹1)

␴

⫺b⫺1

at r ⫽

␴

(

␴

⫹b⫹3)

␴

⫺b⫺1

Using the standard settings

␴

⫽ 10,b⫽ 8 3, the Hopf bifurcation point is

⫽ 24.74. As the periodic orbits created at this subcritical Hopf bifurcation are

followed to the left toward r ⫽ 13.926 in Figure 11.26, their periods continuously

489