Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables

Подождите немного. Документ загружается.

Case e experiences a diﬀerent type of event—symbolized by a rectangle—that aﬀects

his or her risk for the event of interest. Inﬂuential events of this type are typically mod-

eled as time-varying covariates, a topic taken up below. In sum, cases a, b, c, and e are

all easily accommodated in standard survival analyses.

Other cases pose particular problems that may or may not be tractable. Case f has

inception of risk at some time prior to its coming under observation at t

. The dura-

tion over which f is at risk prior to t

is indicated by the dotted line. For case f, incep-

tion of risk is known. Case i is similar except that inception of risk is unknown. Both

f and i are said to have left-truncated survival times. In survival analysis people are

said to have left-truncated survival times whenever they have been at risk for the

event of interest for some period prior to the start time of the study. As in previous

chapters, truncation refers to the situation in which respondents are observed only

when their responses are above or below some threshold value. In this instance,

observation of survival times for left-truncated cases is predicated on their survival

in the nonevent state up to the start of the study. Hence, if t

is the duration of sur-

vival before the start of the study and T denotes survival time, in general, left-truncated

observations are observed only when T ⬎ t

. Left truncation is fairly common in panel

studies in which respondents in a given state at time 1 are tracked in subsequent sur-

veys to see if they experience the event of interest. As an example, the author fol-

lowed married as well as unmarried cohabiting couples in wave 1 of the NSFH to

explore whether intimate violence reported at time 1 predicted separation or divorce

NATURE OF SURVIVAL DATA 385

Figure 11.1 Schematic of event history data for single nonrepeatable events.

c11.qxd 8/27/2004 2:56 PM Page 385

by wave 2 (DeMaris, 2000). As virtually all of these unions were begun prior to the

date of the wave 1 survey, the data were characterized by considerable left truncation.

Below I discuss the diﬃculties associated with left truncation, along with simple reme-

dies for the problem when the inception time is known, as with case f. When this time

is unknown, the problem is considerably less tractable.

The remaining cases pose more serious problems for survival models. Case d expe-

riences the event of interest but inception of risk and time of event occurrence both take

place after the study is completed. This type of case is referred to as being fully right-

censored (Yamaguchi, 1991) and is not amenable to analysis using survival techniques.

Similarly, cases g and h experience the event of interest before the start of the study.

As an example, suppose that we were to follow a group of 12-year-olds to observe the

length of time before they smoke their ﬁrst cigarette. However, some children in the

sample have already begun smoking but cannot remember the date on which that

occurred. Assuming that inception of risk begins at birth, all we know of such children

is that survival time is less than 12 years. These types of cases are accordingly known

as left-censored survival times (Collett, 1994; Hosmer and Lemeshow 1999) and are

also not very amenable to survival modeling.

A ﬁnal concept of central importance that can be gleaned from Figure 11.1 is the

risk set. This is the set of people who are at risk for event occurrence at any given

time t. For example, the risk set at time t

in the ﬁgure consists of cases a, b, c, e, f,

and i. Immediately after case f has been censored, the risk set consists of cases a, b,

c, e, and i. Immediately before case c experiences the event, however, the risk set

only consists of cases a and c, since cases b, e, f, and i have either experienced the

event (cases e and i) or have been censored (cases b and f) at an earlier time.

Critical Functions of Time: Density, Survival, Hazard

In survival models, three functions of time are particularly important: the density

function, the survival function, and the hazard function. The three are also closely

interrelated, so that given any two, the third is readily calculated. First, we note that

survival time, denoted by T, is a random variable ranging from zero to inﬁnity, which

like any other variable, has population distribution and density functions. Certain den-

sities not featured elsewhere in this book are especially important in survival models.

Examples are the exponential, Weibull, Gompertz, and log-logistic densities. (The

exponential density was introduced in the Chapter 1 appendix.) As the exponential

function is very easy to work with, I use it to illustrate the three functions discussed

in this section. If survival time has an exponential distribution, its density function is

f(t) ⫽ λ exp(⫺λt),

where λ is a positive constant. For example, if survival time in days after contract-

ing some disease has an exponential distribution with λ ⫽ .35, the density function

at a time of 15 days is

f(15) ⫽ .35 exp[⫺(.35)(15)] ⫽ .0018.

386 INTRODUCTION TO SURVIVAL ANALYSIS

c11.qxd 8/27/2004 2:56 PM Page 386

Recall that as the density of a continuous variable is not a probability, this value has

no intuitive interpretation.

In general, the distribution function for survival time is

F(t) ⫽ P(T ⱕ t) ⫽ 

f(u) du.

As is evident, F(t) is just the probability that T is less than or equal to t, and the inte-

gration symbol simply denotes that this function is found by integrating, or summing

up, the area under the density curve between 0 and t. For the exponential distribution,

we have

F(t) ⫽ 1 ⫺ exp(⫺λt).

In the example just given, the distribution function evaluated at 15 days is

F(15) ⫽ 1 ⫺ exp[⫺(.35)(15)] ⫽ .995.

This means that the probability of dying within 15 days’ time is .995.

The survival function, denoted S(t), is simply P(T ⬎ t), that is, the probability of

surviving beyond time t. For the exponential density,

S(t) ⫽ 1 ⫺ P(T ⱕ t) ⫽ 1 ⫺ [1 ⫺ exp(⫺ λt)] ⫽ exp(⫺ λt).

To continue with the example, the probability of surviving beyond 15 days is

S(15) ⫽ exp[⫺(.35)(15)] ⫽ .0052.

The interpretation is that there is only a .52% chance of surviving beyond 15 days.

Of central importance in survival analysis is the hazard function. In fact, the log of

the hazard function is most often the response variable in survival regression, giving

rise to models known as hazard models. Ideally, what we would like to model is the

probability of experiencing the event of interest exactly at time t. (In discrete-time

models, we can employ this as the response variable.) However, the probability that a

continuous variable—in this case, time—takes on any speciﬁc value in its range is

zero. So, instead, we deﬁne the hazard as follows. First, let ∆t represent some small

increment in time. Then consider the probability that the event occurs in some small

time interval, say between t and t ⫹ ∆t, conditional on its not having occurred yet. This

probability is denoted

P(t ⱕ T ⬍ t ⫹ ∆t  T ⬎ t).

If we further divide this probability by ∆t, we would have the conditional probabil-

ity of event occurrence in some small time interval per unit of time, or the rate of

event occurrence in a small time interval. The hazard at time t, denoted h(t), is then

NATURE OF SURVIVAL DATA 387

c11.qxd 8/27/2004 2:56 PM Page 387

the limit of this rate as the time interval shrinks to zero. Formally, we have

h(t) ⫽ lim

∆t→0

. (11.1)

The hazard in continuous time can be interpreted as the instantaneous rate of event

occurrence, or as Blossfeld et al. (1989, p. 31) describe, it is “. . . the instantaneous

probability that episodes in the interval [t, t ⫹ ∆t] are terminating provided that the

event has not occurred before the beginning of this interval.”

Relationships between the hazard, survival, and density functions follow from the

foregoing deﬁnitions. Now, the density function is the ﬁrst derivative of the distri-

bution function. Thus, the density function can be written as

f(t) ⫽ F⬘(t) ⫽ lim

∆t→0

ᎏ

F(t ⫹ ∆

∆

) ⫺ F(t)

ᎏ

⫽ lim

∆t→0

ᎏ

P(t ⱕ T

∆

⬍

t ⫹ ∆t)

ᎏ

and by the rules for conditional probabilities,

P(t ⱕ T ⬍ t ⫹ ∆t  T ⱖ t) ⫽⫽.

Therefore, h(t) can be written as

h(t) ⫽ lim

∆t→0

⫽ lim

∆t→0

⫽ lim

∆t→0

⫽

ᎏ

(

)

ᎏ

. (11.2)

In other words, the hazard function is the ratio of the density function to the survival

function. Notice the similarity to the hazard function of the normal distribution—

lambda—as deﬁned in Chapter 9. Equation (11.2) implies further that f(t) ⫽ h(t)S(t).

Employing equation (11.2), we ﬁnd that the hazard function for the exponential

distribution is

h(t) ⫽

ᎏ

(⫺

ᎏ

⫽ λ.

As this is a constant rather than a function of t, the exponential distribution is said to

have a constant hazard. In other words, the hazard of event occurrence remains con-

stant over time. As this may be unrealistic for many applications, other distributions,

such as the Weibull, allow for the hazard to change over time. However, the focus in

this chapter is on a semiparametric modeling approach for the log hazard, or ln[h(t)],

that does not depend on the choice of distribution for survival time. I therefore omit

detailed discussion of more complex distributions.

P(t ⱕ T ⬍ t ⫹ ∆t)/∆t

ᎏᎏᎏ

P(T ⱖ t)

P(t ⱕ T ⬍ t ⫹ ∆t)/P(T ⱖ t)

ᎏ

ᎏᎏᎏ

∆t

P(t ⱕ T ⬍ t ⫹ ∆t  T ⱖ t)

ᎏᎏᎏ

∆t

P(t ⱕ T ⬍ t ⫹ ∆t)

ᎏᎏ

P(T ⱖ t)

P(t ⱕ T ⬍ t ⫹ ∆t傽T ⱖ t)

ᎏᎏᎏ

P(T ⱖ t)

P(t ⱕ T ⬍ t ⫹ ∆t  T ⱖ t)

ᎏ

ᎏᎏ

ᎏ

∆t

388 INTRODUCTION TO SURVIVAL ANALYSIS

c11.qxd 8/27/2004 2:56 PM Page 388

Example: Dissolution of Intimate Unions

To illustrate the concepts just discussed, and in particular, to give a sense of the sur-

vival and hazard functions, I consider data drawn from both waves of the NSFH on

the dissolution of married and unmarried cohabiting relationships. The example is

based on a larger study (DeMaris, 2000) that examined the impact of intimate vio-

lence on union disruption. Whereas that study included all married and cohabiting

couples who had been together for up to 20 years in wave 1, the present example is

limited to the 1230 couples who had been together for at most three years in wave 1.

Five to seven years later, in the wave 2 survey, the same couples were queried as to

whether they were still together. If they had split up, they were asked to give the

dates of separation or divorce. For consistency between cohabitors and marrieds, the

date of separation was employed to index the event of union disruption. The few

couples experiencing the death of either partner were considered censored as of the

date of death. Because most couples had been in their unions for some time (any-

where from 0 to 3 years) before being initially surveyed, the data are left-truncated.

Nevertheless, I will begin by ignoring this problem and treat couples as though they

were all observed from inception of risk. Later I adjust the analyses for left trunca-

tion and compare results.

Nonparametric Estimation of S( t) and h( t). A ﬁrst step in survival analysis

typically involves examining survival and hazard functions for the sample as a

whole, ignoring potential diﬀerences among people induced by explanatory variables.

Table 11.1 presents nonparametric estimators of S(t) and h(t) for the 1230 couples

NATURE OF SURVIVAL DATA 389

Table 11.1 Life-Table Estimates of Survival and Hazard Functions for the Event

of Union Disruption

Time Number Number Risk Conditional Survival Hazard

Interval Failed Censored Set P(Failure) Function Function

[0, 6) 52 0 1230.0 .0423 1.0000 .0072

[6, 12) 35 1 1177.5 .0297 .9577 .0050

[12, 18) 45 0 1142.0 .0394 .9293 .0067

[18, 24) 27 3 1095.5 .0246 .8926 .0042

[24, 30) 28 2 1066.0 .0263 .8706 .0044

[30, 36) 30 2 1036.0 .0290 .8478 .0049

[36, 42) 30 0 1005.0 .0299 .8232 .0051

[42, 48) 16 3 973.5 .0164 .7986 .0028

[48, 54) 17 2 955.0 .0178 .7855 .0030

[54, 60) 18 32 921.0 .0195 .7715 .0033

[60, 66) 25 161 806.5 .0310 .7565 .0052

[66, 72) 19 348 527.0 .0361 .7330 .0061

[72, ⬁) 6 328 170.0 .0353 .7066

Total 348 882

c11.qxd 8/27/2004 2:56 PM Page 389

in the sample. The method employed here is the life-table approach (Blossfeld

et al., 1989). This technique involves partitioning survival time into a series of q ⫹ 1

nonoverlapping time intervals of the form [0,a

), [a

),..., [a

,⬁), where a

indicates the kth value of time and then using the censored and uncensored cases in

each interval to estimate the two functions. (Recall that “[a

)” means that the

interval includes a

but not a

.) In the current case, since the follow-up interval

between survey waves ranged between about ﬁve and seven years, survival time in

months from the wave 1 interview until either disruption or censoring ranged from

0 to 86. This time period was then partitioned into 6-month intervals, except for

the last period, which encompassed months 72 or later. The last interval, shown as

“[72,⬁)” in the table, was made larger because there were so few disruptions after

month 72.

We ﬁrst estimate the conditional probability of failure for a given interval. Letting

represent the number of disruptions, or “failures” in the kth interval, w

represent

the number of cases censored in the kth interval, and R

represent the number of indi-

viduals who had no event until the beginning of the kth interval, the conditional

probability of failure for the kth interval is (Blossfeld et al., 1989):

⫽

ᎏ

⫺

ᎏ

, (11.3)

where the denominator is an estimator of the risk set for the kth interval. If there are

no censored cases, λ

is simply d

. However, this simpler computation would

tend to underestimate the actual hazard rate in the presence of censoring (Blossfeld

et al., 1989). Hence, one-half of the number of censored cases is subtracted from R

in (11.3). The reasoning here is that if censored observations are assumed to be uni-

formly distributed over the interval, the average size of the risk set in the interval is

⫺ w

/2 (Hosmer and Lemeshow, 1999). As an example, R

is 1230, and there are

no censored cases, so the ﬁrst conditional probability of failure is simply 52/1230 ⫽

.04227 or .0423. In the second interval, we start with 1230 ⫺ 52 ⫽ 1178 couples who

have had no event so far. There is one censored case in this interval, so the risk set

is 1178 ⫺

ᎏ

⫽ 1177.5, and λ

⫽ 35/1177.5 ⫽ .0297. Now, the risk set for the next

interval must remove the remaining censored cases plus the 35 uncensored cases,

and there are no new censored cases, so it is calculated as 1177.5 ⫺

ᎏ

⫺ 35 ⫽ 1142.

The remaining computations proceed in a similar fashion.

The conditional probability of failure is used to construct estimates of both the

survival and hazard functions. First, let

pˆ

⫽ 1 ⫺ λ

be the conditional probability of

survival through the kth interval, given survival through the preceding interval. For

example, 1 ⫺ .0423 ⫽ .9577 is the conditional probability of surviving through the

ﬁrst interval, and 1 ⫺ .0297 ⫽ .9703 is the conditional probability of surviving through

the second interval. The survival function estimate, S

, is constructed as the product

of these conditional probabilities. That is, the survival function estimate for the kth

interval is

⫽ (pˆ

)(pˆ

k ⫺ 1

)(pˆ

k ⫺ 2

)

...

(pˆ

390 INTRODUCTION TO SURVIVAL ANALYSIS

c11.qxd 8/27/2004 2:56 PM Page 390

In SAS’s PROC LIFETEST, which was used for Table 11.1, the survival function is

the proportion of the sample surviving to the beginning of the interval, hence pˆ

always 1. For the second interval, S

⫽ (1)(1 ⫺ .0423) ⫽ .9577, which is the propor-

tion surviving up to the second interval. The proportion surviving until the third

interval is then (1)(.9577)(1 ⫺ .0297) ⫽ .9293, and so on.

Finally, an estimator of the average hazard rate at the midpoint of the kth interval

is (Blossfeld et al., 1989)

⫽

ᎏ

(

⫺

)

ᎏ

where L

⫽ a

⫺ a

k ⫺ 1

is the length of the kth interval. Thus,

⫽

ᎏ

(

⫺

.04

)

ᎏ

⫽ .0072.

The other estimates in the column “hazard function” are computed in similar

fashion. (No hazard estimate is shown for the 13th interval, as L

cannot be

computed.) Plots of the survival and hazard functions from Table 11.1 against the

lower limits of the time intervals are shown in Figures 11.2 and 11.3. The survival

NATURE OF SURVIVAL DATA 391

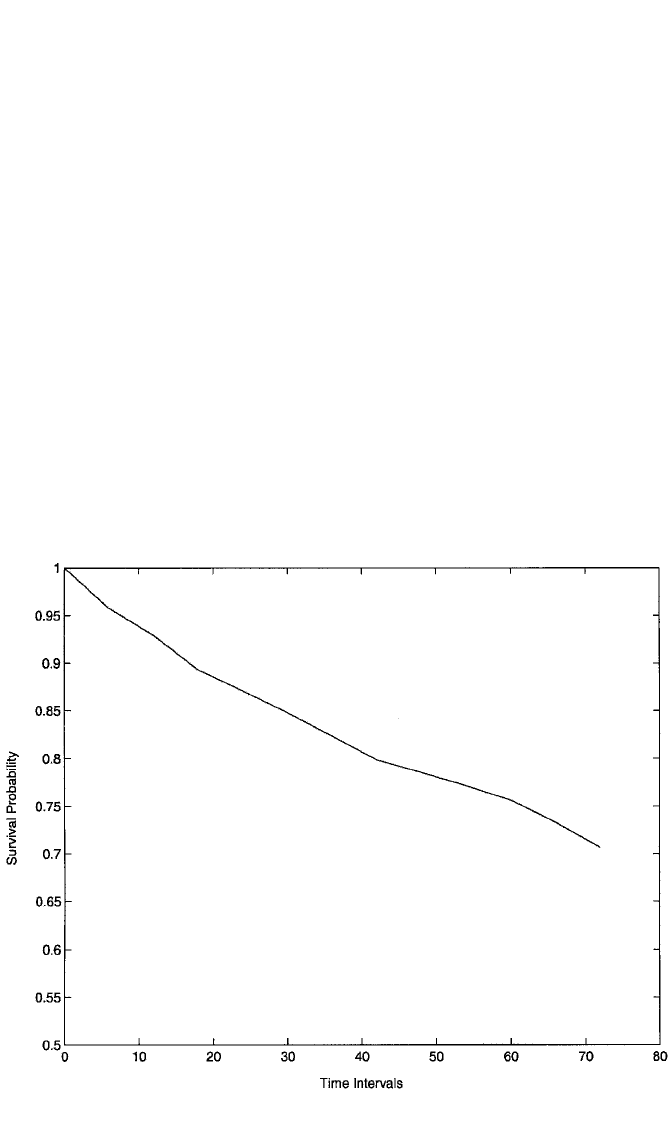
Figure 11.2 Life-table estimator of survival function for event of union disruption.

c11.qxd 8/27/2004 2:56 PM Page 391

function exhibits a relatively smooth decline from a high of 1 at the start of the

process, to a minimum of .7066 for the interval with a lower limit of 72 months.

Apparently, slightly over 70% of relationships survived for at least 72 months

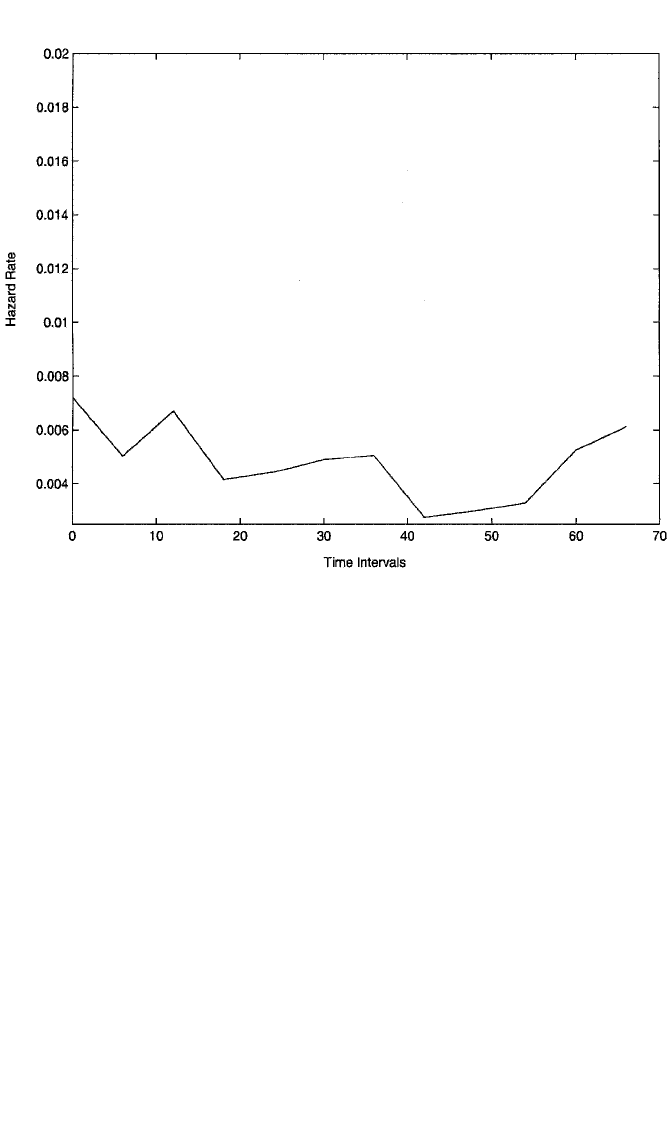
intact. The hazard function, on the other hand, displays a more erratic trend; there

appears to be no clear upward or downward pattern. The greatest hazard of

disruption is apparently in the ﬁrst six-month interval, although the last interval’s

hazard is almost as high. Nonetheless, all of the hazards are quite low, with the

highest being only .0072.

Examining Parametric Forms for the Hazard Function. As Blossfeld et al. (1989)

explain, nonparametric estimates of the survival function can be used to suggest a

potential parametric model for the log of the hazard function. In particular, a plot of

various functions of S

(t) against time can be used to reveal which density function is

most appropriate for survival time. As we will see below, if a parametric distribution

for time can be identiﬁed, we can take advantage of maximum likelihood estimation

in regression models for ln[h(t)], which confers certain beneﬁts (e.g., asymptotic

eﬃciency) over alternative estimation techniques. To understand the idea behind these

transformations, we again examine the exponential density. Recall that its survival

function is S(t) ⫽ exp(⫺λt). Taking logs of both sides of this equation and multiplying

both sides by ⫺1, we have ⫺ln S(t) ⫽ λt. That is, ⫺ln S(t) is a linear function of time

392 INTRODUCTION TO SURVIVAL ANALYSIS

Figure 11.3 Life-table estimator of hazard function for event of union disruption.

c11.qxd 8/27/2004 2:56 PM Page 392

with an intercept of zero. Therefore, if time has an exponential distribution, a plot of

⫺ln S

(t) against time should form a straight line through the origin.

Similarly, a Weibull distribution is supported if a plot of ln[⫺ln S

(t)] against the log

of time produces a straight line. On the other hand, if the function ln(ln[S

(t)/ S

(t ⫹ 1)])

has a linear relationship with time, a Gompertz distribution is supported. In this case,

t and t ⫹ 1 represent adjacent times or time intervals. Finally, if the function

ln[(1 ⫺ S

(t))/S

(t)] has a linear relationship with the log of time, a log-logistic distribu-

tion for survival time is indicated. Rather than relying on visual inspection alone, one

can regress the relevant transformation of S

(t) on time and include quadratic or cubic

terms in time to test for nonlinear eﬀects. When this was done with the life-table esti-

mates of S(t) from Table 11.1, the exponential, Weibull, and log-logistic distributions

were all supported. However, as the exponential distribution is the most parsimonious

of the three, and as the plot in Figure 11.3 is consistent with a constant hazard, I will

choose the exponential distribution for survival time, at least to start with.

REGRESSION MODELS IN SURVIVAL ANALYSIS

The hazard function depicted in Figure 11.3 assumes that all people have the same

hazard at any given time. This is, of course unrealistic, since individual characteris-

tics will typically raise or lower the hazards for certain people compared to others.

One way to introduce individual heterogeneity, or variability, into the hazard func-

tion is to model ln[h(t)] as a function of a set of covariates representing people’s

attributes, giving rise to regression models for the log of the hazard function. In this

section of the chapter I begin with a parametric model: in particular, the exponential

model. As programs for the estimation of parametric models (e.g., PROC LIFEREG

in SAS) usually model the log of survival time, rather than the log of the hazard, I

begin with log survival-time models.

Accelerated Failure-Time Model

Letting T

denote the survival time for the ith person, parametric models take the form

ln T

⫽ x

⬘

ββ

⫹ σε

, (11.4)

where σ is a parameter to be estimated and ε

is a random disturbance term whose

density determines the parametric form of the model. For example, the exponential

model is speciﬁed by constraining σ to equal 1 and assuming that ε

has a Gumbel

distribution (Allison, 1995), since this speciﬁcation implies an exponential distribu-

tion for survival time. As noted, the exponential model assumes that the hazard of

the event of interest is constant over time. A Weibull model would be speciﬁed by

retaining the Gumbel distribution for ε

but allowing σ to depart from the value of 1.

If σ ⬎ 1, the hazard is decreasing with time. If σ is between .5 and 1, the hazard is

increasing at a decreasing rate. If σ is between 0 and .5, the hazard is increasing at

an increasing rate. And if σ ⫽ .5, the hazard is increasing at a constant rate (Allison,

REGRESSION MODELS IN SURVIVAL ANALYSIS 393

c11.qxd 8/27/2004 2:56 PM Page 393

1995). Models of the form in equation (11.4) are referred to as accelerated failure-time

(AFT) models. The reason for this is that if we exponentiate both sides of equation

(11.4), we get

⫽ exp(x

⬘

ββ

⫹ σε

) ⫽ e

σε

which makes it clear that increases in covariate values either accelerate or deceler-

ate the survival (or, conversely, the failure) time.

Maximum Likelihood Estimation. Assuming that the disturbance term in equation

(11.4) has a Gumbell distribution allows us to estimate the parameters of this equation

via maximum likelihood. To form a general expression for the likelihood function for

survival data, we reason as follows. First, let c

be the censoring indicator for the ith

person, coded 1 if the person is uncensored, and 0 if censored. (This seems like back-

ward coding for a dummy variable but is conventional coding in survival analysis.)

Then, for the ith uncensored case, let f(t

ββ

, x

) be that case’s density at time T ⫽ t

given parameter vector

ββ

and covariate vector x. Similarly, for the ith censored case,

let S(t

ββ

, x

) be that case’s survivor function, or probability of survival through time

T ⫽ t

, given parameter vector

ββ

and covariate vector x. A general expression for the

likelihood function for n sample cases is then (Hosmer and Lemeshow, 1999)

ββ

t,x) ⫽ 

i⫽1

{[f(t

ββ

, x

)]

[S(t

ββ

, x

)]

1⫺c

(11.5)

Notice that all of the sample information regarding event and censoring times is

being exploited in expression (11.5). Taking logs of both sides of this function, a

general expression for the log of the likelihood function is

ln L(

ββ

t,x) ⫽



i⫽1

ln[f(t

ββ

, x

)] ⫹ (1 ⫺ c

) ln[S(t

ββ

, x

)]}

(11.6)

To construct the likelihood for the exponential model, we must ﬁrst specify its

density and survival functions. First, to simplify notation somewhat, we rewrite the

exponential model letting Y

⫽ ln T

and imposing the constraint that σ ⫽ 1:

⫽ x

⬘

ββ

⫹ ε

. (11.7)

Then note that in general, if X has a Gumbel distribution, its density function is

f(x) ⫽ exp(x ⫺ e

), (11.8)

whereas its survival function is

S(x) ⫽ exp(⫺e

). (11.9)

Recall that ε

in equation (11.7) has a Gumbel distribution, and notice that this equa-

tion also implies that ε

can be written as y

⫺ x

⬘

ββ

. Then, substituting y

⫺ x

⬘

ββ

for x

394 INTRODUCTION TO SURVIVAL ANALYSIS

c11.qxd 8/27/2004 2:56 PM Page 394