Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables

Подождите немного. Документ загружается.

Letting x

⫺j

be the collection of all other regressors:

E(Y 冟 x

⫹ 1, x

⫺j

) ⫺ E(Y 冟 x

, x

⫺j

) ⫽ exp[β

⫹ β

⫹

...

⫹ β

⫹ 1) ⫹

...

⫹ β

]

⫺ exp(β

⫹ β

⫹

...

⫹ β

⫹

...

⫹ β

It should be clear that this expression does not simplify further. The partial deriva-

tive of µ

with respect to X

, on the other hand, is

ᎏ

∂

ᎏ

⫽

ᎏ

∂

ᎏ

[exp(β

⫹ β

⫹

...

⫹ β

⫹

...

⫹ β

)]

⫽β

exp(β

⫹ β

⫹

...

⫹ β

⫹

...

⫹ β

) ⫽ β

. (10.3)

This shows that the eﬀect of the jth regressor is not constant, but rather, depends on

the levels of all covariates, since β

changes with µ

. However, if we divide expres-

sion (10.3) by µ

, we can isolate β

. As the partial derivative is the change in the

response for an inﬁnitesimal increase in the predictor at a given predictor value, β

can be interpreted as the proportional change in µ

(as a proportion of µ

) with an

inﬁnitesimal increase in X

at x

A more appealing interpretation can be found by exponentiating β

. Called the

factor change by Long (1997, p. 225), exp(β

) is the multiplicative change in the

expected count for each unit increase in X

, net of the other regressors. To see this,

consider the ratio of expected counts for those who are 1 unit apart on X

⫽

⫽ exp(β

In other words, E(Y 冟 x

⫹ 1, x

⫺j

) ⫽ exp(β

)E(Y 冟x

, x

⫺j

), which shows that a 1-unit

increase in x

multiplies the expected count by exp(β

), controlling for the other

regressors. The proportionate change in the expected count for a unit increase in

⫽⫺1⫽ exp(β

)⫺1,

(10.4)

and therefore the percent change in the expected count for a 1-unit increase in X

100[exp(β

) ⫺ 1]. If X

is a dummy variable, exp(β

) represents the ratio of expected

counts for those in the interest, versus the reference, categories, and expression

(10.4) represents the proportion by which being in the interest category compared to

the reference category increases or decreases the expected count.

E(Y 冟x

⫹1, x

⫺j

)

ᎏᎏ

E(Y 冟x

, x

⫺j

)

E(Y 冟x

⫹1, x

⫺j

) ⫺ E(Y 冟 x

, x

⫺j

)

ᎏᎏᎏ

E(Y 冟x

, x

⫺j

)

exp(β

) exp(β

)

...

exp(β

) exp(β

)

...

exp(β

)

ᎏᎏᎏᎏᎏᎏ

exp(β

) exp(β

)

...

exp(β

)

...

exp(β

)

exp(β

⫹ β

⫹

...

⫹ β

⫹ 1) ⫹

...

⫹ β

)

ᎏᎏᎏᎏᎏ

exp(β

⫹ β

⫹

...

⫹ β

⫹

...

⫹ β

)

E(Y 冟x

⫹1, x

⫺j

)

ᎏᎏ

E(Y 冟x

, x

⫺j

)

MODELING COUNT RESPONSES WITH POISSON REGRESSION 355

c10.qxd 8/27/2004 2:56 PM Page 355

356 REGRESSION MODELS FOR AN EVENT COUNT

A number of statisticians give a unit proportional impact interpretation to β

. For

example, Cameron and Trivedi (1998, p. 81) say: “The coeﬃcient β

equals the

proportionate change in the conditional mean if the jth regressor changes by one

unit.” As expression (10.4) shows, this is not technically correct. However, it is

approximately correct whenever a unit change in X

equals a very small change in

that variable, which is what statisticians have in mind when they imbue β

with this

interepretation. In the latter case, β

should be a value close to zero, and exp(β

) is

then approximately equal to 1 ⫹ β

. For example, if β

⫽ .05, then exp(.05) ⫽ 1.051.

In this scenario, exp(β

) ⫺ 1 艐 1 ⫹ β

⫺ 1 ⫽ β

, and the unit proportional impact inter-

pretation for β

is then appropriate. Otherwise, expression (10.4) provides the correct

proportionate change in the expected count for unit increases in X

Example. Table 10.1 presents both OLS and PRM estimates for the regression of

number of previous math courses on several characteristics of students: age over 21

(a dummy for whether students are over 21), male (a dummy for being male), social

sciences major (a dummy for majoring in a social science other than sociology, with

sociology majors as the contrast group), other major (a dummy for majoring in other

than a social science ﬁeld, with sociology majors as the contrast group), classiﬁ-

cation (student classiﬁcation), high school GPA, and college GPA. Substantively, the

models provide similar conclusions about the nature of regressor eﬀects. Both

models are signiﬁcant as a whole. The F statistic for the model estimated with OLS

is 7.67; with 7 and 222 degrees of freedom, this is signiﬁcant at the .0001 level.

Similarly, the model χ

for the PRM of 43.862, with 7 degrees of freedom, is also

Table 10.1 Unstandardized OLS and PRM Estimates for the Regression of Number

of Previous Math Courses

OLS PRM

Regressor btbzexp(b)

Intercept ⫺1.551 ⫺2.311 ⫺1.951 ⫺3.287 .142

Age over 21 .265 1.595 .187 1.330 1.206

Male .436 2.877 .313 2.548 1.368

Social sciences major

⫺.052 ⫺.255 ⫺.028 ⫺.154 .972

Other major

⫺.024 ⫺.144 .037 .258 1.038

Classiﬁcation .402 4.143 .336 3.723 1.399

High school GPA .547 3.486 .395 2.914 1.484

College GPA ⫺.190 ⫺1.323 ⫺.174 ⫺1.375 .840

F/model χ

7.670 43.862

.195

.207

.067

.179

Note: n ⫽ 230.

Sociology major is the reference category.

c10.qxd 8/27/2004 2:56 PM Page 356

signiﬁcant at the .0001 level. Three predictors are signiﬁcant in both models, and in

similar directions. Males, students with higher classiﬁcations (e.g., seniors, as

opposed to sophomores) and those with higher high school GPAs all have a higher

expected number of previous math courses, compared to others. The coeﬃcients

cannot be directly compared, however. For example, the OLS results suggest that

men have a mean number of previous math courses that is higher by .436, compared

to females. The PRM model’s coeﬃcient suggests that men’s expected count of

previous math courses is 36.8% higher than women’s. The coeﬃcient for high school

GPA in OLS implies that each unit increase in high school GPA adds .547 to the

expected count. The PRM coeﬃcient, on the other hand, suggests that the expected

count increases by 48.4% for each unit increase in high school GPA.

The linear regression model gives negative predicted mean math-course counts—

which are clearly untenable values—at certain covariate patterns. For example, a stu-

dent who is a sophomore female social science major, under 21 years of age, with a

high school GPA of 2.5 and a college GPA of 3.5 has a predicted mean math-course

count of ⫺ 1.551 ⫺ .052 ⫹ .402(2) ⫹ .547(2.5) ⫺ .19(3.5) ⫽⫺.097. In the PRM, on

the other hand, this student’s expected count is exp[⫺ 1.951 ⫺ .028 ⫹ .336(2) ⫹

.395(2.5) ⫺ .174(3.5)] ⫽ .395. The PRM also allows us to generate a predicted

probability for any given count of previous math courses, based on the parameter

estimates. Using the formula for the Poisson probability, the predicted probability of

a particular value of Y for the ith case is

冟 x

ββ

) ⫽

ᎏ

⫺

ᎏ

Notice that this depends on the case’s covariates, since µ

varies with the covariates.

Hence, for any given value of Y, there are potentially n diﬀerent predicted probabil-

ities for that value. As an example, let’s calculate the probability of having had three

previous math courses for a senior male social science major, over 21 years of

age, with a high school GPA of 2.8 and a college GPA of 3.1. First, the expected

math-course count for this student is exp[⫺ 1.951 ⫹ .187 ⫹ .313 ⫺ .028 ⫹ .336(4) ⫹

.395(2.8) ⫺ .174(3.1)] ⫽ 1.54. Then, the predicted probability of having had three

math courses for this student is

(3) ⫽

ᎏ

⫺1.54

(

1.54)

ᎏ

⫽ .13.

Empirical Consistency and Discriminatory Power

Empirical Consistency. There are few formal tests of empirical consistency for

count models [but see Cameron and Trivedi (1998) and Greene (2003) for some sug-

gested approaches]. However, one means of informally assessing whether the data

behave according to model predictions is to compare the observed sample propor-

tions of cases having each value of Y with the mean predicted probability of each

value of Y, where the mean is taken over all n cases (Cameron and Trivedi, 1998;

Long, 1997). The mean predicted probability that Y ⫽ y, based on a PRM, is denoted

MODELING COUNT RESPONSES WITH POISSON REGRESSION 357

c10.qxd 8/27/2004 2:56 PM Page 357

358 REGRESSION MODELS FOR AN EVENT COUNT

, and is calculated as

⫽

ᎏ

冱

i⫽1

ᎏ

⫺

ᎏ

As is evident, p

is simply the average predicted probability of y across all n cases.

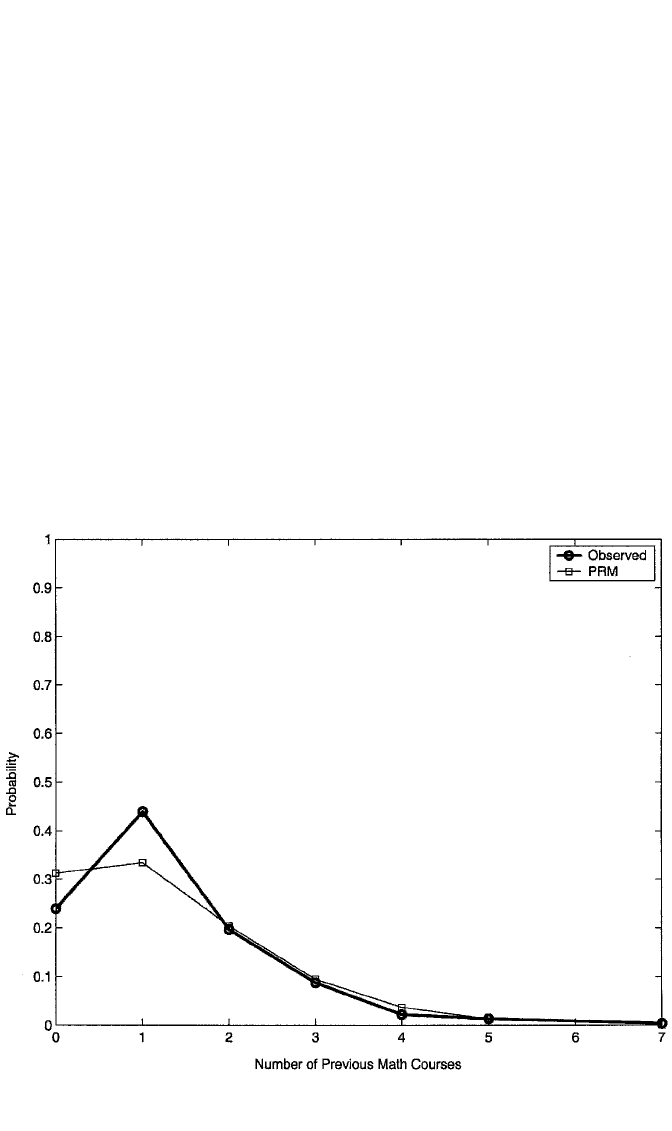
Figure 10.4 shows a plot of p

, based on the PRM in Table 10.1, against the observed

proportions of students having each number of previous math courses. The PRM

appears to ﬁt the sample proportions quite closely for counts of 2 or more. However,

the ﬁt appears to be poor for counts of zero or one previous math course. Apparently,

the PRM overpredicts zero counts and underpredicts counts of 1. Below we consider

whether the PRM is really an appropriate model for this response.

Discriminatory Power. As is the case in logistic regression, there is no single coun-

terpart in count models to the R

in linear regression for measuring discriminatory

power. Hence, I will discuss three diﬀerent R

analogs that have been proposed.

First, we should recall from Chapter 7 that the R

in linear regression exhibits two

properties that are highly desirable in any measure of discriminatory power: it falls

Figure 10.4 Observed versus mean predicted probabilities for number of previous math courses, with

predictions based on the PRM.

c10.qxd 8/27/2004 2:56 PM Page 358

MODELING COUNT RESPONSES WITH POISSON REGRESSION 359

within the range of 0 to 1, and it is nondecreasing as regressors are added to a model.

The ﬁrst measure I consider is the likelihood-ratio index, also considered for logis-

tic regression models. The formula in count models is essentially the same:

⫽ 1 ⫺

ᎏ

where L

is the likelihood for the estimated model, evaluated at its MLEs, and L

the likelihood for the intercept-only model. This measure is nondecreasing as pre-

dictors are added, since the likelihood never decreases as parameters are added to the

model. (If the likelihood could decrease with addition of predictors, ln L

, which

is a negative value, could become larger in magnitude, implying a smaller R

.) In

logistic regression, this measure is also bounded by 0 and 1. However, in count mod-

els, this measure cannot attain its upper bound of 1 (Cameron and Trivedi, 1998),

and so may underestimate the discriminatory power of any particular model.

A second analog employed by some statisticians (Land et al., 1996) is the corre-

lation between Y and its predicted value according to the model. Recall that this

gives us the R

for linear regression. Hence, this measure is r

⫽ [corr( y,µ

)]

Although this measure is bounded by 0 and 1, it is not necessarily nondecreasing

with the addition of parameters. The advantage to these ﬁrst two measures, on the

other hand, is that they are readily calculated from output produced by count-model

software.

The third measure, proposed by Cameron and Windmeijer (1997), is the deviance

. It is deﬁned as follows. First, we deﬁne the Kullback–Leibler (KL) divergence,

a measure of the discrepancy between two likelihoods. Let y be the vector of

observed counts and

µµ

be the vector of predicted counts based on a given model.

Further, let 艎(

µµ

,y) be the log-likelihood for the intercept-only model, 艎(

µµ

,y) the

log-likelihood for the hypothesized model, and 艎(y,y) the maximum log-likelihood

achievable. This last would be the log-likelihood for a saturated model, one with as

many parameters as observations. Then the KL divergence between saturated and

intercept-only models, K(y,

µµ

), equals 2[艎(y,y) ⫺ 艎 (

µµ

,y)]. This represents an esti-

mate of the information on y, in sample data, that is “potentially recoverable by

inclusion of regressors” (Cameron and Windmeijer, 1997, p. 333) and corresponds

to the TSS in linear regression. The information on y that remains after regressors are

included in the model is the KL divergence between saturated and ﬁtted models,

K(y,

µµ

), which is equal to 2[艎(y,y)⫺ 艎(

µµ

,y)]. This is analogous to the SSE in linear

regression. Finally, the deviance R

⫽1⫺

The reader should recognize that the right-hand side of R

is analogous to

1 ⫺ SSE/TSS, the R

in linear regression. In this application, however, R

does not

have an “explained variance” interpretation. Rather, it is “the fraction of the maximum

potential likelihood gain (starting with a constant-only model) achieved by the ﬁtted

model” (Cameron and Windmeijer, 1997, p. 338). R

possesses both of the other

properties of a desirable R

analog: It is bounded by 0 and 1 and it is nondecreasing

K(y,

µµ

)

ᎏ

K(y,

µµ

)

c10.qxd 8/27/2004 2:56 PM Page 359

360 REGRESSION MODELS FOR AN EVENT COUNT

with the addition of parameters. Moreover, in logit models, where 艎(y,y) ⫽ 0, this

measure reduces to

⫽ 1 ⫺

ᎏ

(

µµ

)

ᎏ

⫽ 1 ⫺

ᎏ

⫺

艎

(

µµ

)

ᎏ

⫽ 1 ⫺

ᎏ

艎

(

µµ

)

ᎏ

⫽ R

The only drawback to R

is that it can be quite tedious to compute, and is not auto-

matically provided in software for count models. An exception is LIMDEP, which

provides R

for PRM models. For other models, however, the LIMDEP user has to

program the calculations for R

Measures of discriminatory power for both OLS and PRM models are shown in

the bottom of Table 10.1. The OLS analysis suggests that 19.5% of the variation in

number of previous math courses is accounted for by the model. The three R

analogs for the PRM have widely diﬀering values, with r

, at .207, being closest to

the OLS R

. R

’s value of .067 suggests that the model is weak, but this measure is

likely to underestimate discriminatory power. The superior measure is R

, which,

with a value of .179, is similar to the OLS R

in suggesting a moderately eﬃcacious

model.

Testing the Equidispersion Hypothesis. The PRM is the most basic of the count-

data models. Typically, it is not the appropriate model for the data because the

equidispersion hypothesis fails. And most often, this is because the data are overdis-

persed. Use of the PRM in the presence of overdispersion results in ineﬃcient

estimators and downwardly biased estimates of standard errors (Cameron and

Trivedi, 1998). Cameron and Trivedi (1998) suggest that a quick diagnostic for this

condition is simply to examine the sample unconditional mean and variance of Y. If

⬍ y

苶

, the data are probably underdispersed, whereas if s

⬎ 2y

苶

, the data are proba-

bly overdispersed. In the latter case, the factor of 2 is suggested, since the inclusion

of covariates will tend to reduce the conditional variance of Y in comparison with the

unconditional variance. It is the conditional variance of Y in relation to the conditional

mean that matters. For number of previous math courses, recall that s

and y

苶

are both

1.274. Given that the conditional variance should be reduced even further by the

regressors, it is likely that the data are actually underdispersed.

One way to test for equidispersion is to compare the PRM to a known alternative

model that allows for under- or overdispersion, which includes the PRM as a special

case. Then a nested chi-squared test is a test for equidispersion. We consider this

type of test below. The drawback, however, is that such a test requires an assumption

of a particular alternative parametric form for the density of Y. A test of the equidis-

persion hypothesis that does not require this assumption has been proposed

by Cameron and Trivedi (1990). Their approach only requires that we specify the

nature of the relationship between the mean and variance of Y. The null hypothesis

for the test is that the mean and variance are equal. That is, H

is V(Y ) ⫽ E(Y ).

The alternative hypothesis, H

, is that the variance is a function of the mean.

Two possible functions that have been considered are V(Y ) ⫽ E(Y ) ⫹ αE(Y ) and

V(Y ) ⫽ E(Y ) ⫹ α[E(Y )

]. In either case, if α is negative, the data are underdispersed,

c10.qxd 8/27/2004 2:56 PM Page 360

and if α is positive, the data are overdispersed. Letting µ stand for E(Y ), the null and

alternative hypotheses are reexpressed as

: E[(Y ⫺ µ)

] ⫽ µ,

: E[(Y ⫺ µ)

] ⫽ µ ⫹ αµ or E[(Y ⫺ µ)

] ⫽ µ ⫹ αµ

This implies the formulation

: E[(Y ⫺ µ)

⫺ Y] ⫽ 0,

: E[(Y ⫺ µ)

⫺ Y] ⫽ αµ or E[(Y ⫺ µ)

⫺ Y] ⫽ αµ

This formulation suggests that a test for whether α ⫽ 0 in the linear regression of

(Y ⫺ µ)

⫺ Y on αµ or αµ

is a test for equidispersion (Cameron and Trivedi, 1990).

With µ

equal to the ﬁtted values from the PRM, Cameron and Trivedi’s test involves

performing a linear regression of [(y

⫺µ

)

⫺ y

]/兹2

苶

on α[g(µ

)/兹2

苶

] ⫹ e, using

OLS, where g(µ

) is either µ

or µ

. (Note that this is a no-intercept model.) The t

test for α

from the regression is the test of H

. For the PRM in Table 10.1, the coeﬃ-

cients for both µ

and µ

were negative (⫺.245, and ⫺.143, respectively) and signi-

ﬁcant, suggesting that the data are underdispersed. King (1989) discusses generalized

event count models that can handle underdispersed data. As such models are not

always readily available in commercial software (but see LIMDEP’s gamma model

for an exception), I will not discuss them further. Below I discuss models for han-

dling overdispersion, the more common situation.

Tobit versus Count-Data Models. At times there may be some confusion about

whether the data call for a tobit model or a count-data model, particularly when the

minimum value of Y is zero. The author has seen the tobit model used on a count

response with the rationale that the count is a proxy for an underlying continuous

variable that is modeled more appropriately using linear regression. Here I brieﬂy

articulate the diﬀerences between these modeling approaches. First, a latent contin-

uous variable can be said to underlie the observed response in both cases: Y* in the

tobit model and µ in the PRM (King, 1989). Nevertheless, there are clear diﬀerences

between these models. In tobit, the latent response is determined by a linear regres-

sion, and negative values of Y* are reasonable. In the PRM, the latent response is an

exponential function of the regressors, and negative values of µ are not possible. In

tobit, Y* ⫽ Y once the censoring threshold has been crossed. In the PRM, µ is never

synonymous with Y. In tobit, zeros represent censored values of Y*—the zero sim-

ply means that Y* is below the threshold. In the PRM, zeros are legitimate counts

and do not represent censoring. Perhaps most important, in tobit, the response is

either continuous or a proxy for a continuous variable. In the PRM, the response is

a count. In short, whenever the response is a count, a count-data model such as the

PRM is the appropriate model.

MODELING COUNT RESPONSES WITH POISSON REGRESSION 361

c10.qxd 8/27/2004 2:56 PM Page 361

362 REGRESSION MODELS FOR AN EVENT COUNT

Truncated PRM

It is commonly the case that count variables are sampled from truncated distribu-

tions. A zero-truncated sample occurs when cases enter the sample conditional on

having experienced at least one event (Long, 1997). For example, in the kids dataset,

a question asks about the number of lifetime sex partners that each oﬀspring has had.

Because the data are limited to households of oﬀspring who have initiated sexual

intercourse, the sample is selective of sexually active oﬀspring. Hence, counts of

zero are not observed. The mean and variance of number of lifetime sex partners for

the 357 oﬀspring in the sample are 6.698 and 36.15, respectively, with a range of 1

to 20 partners. (Notice that the data appear to be overdispersed; this will be

addressed when we discuss the negative binomial regression model below.)

To understand the rationale for the truncated model, consider ﬁrst the following

probability rule: If event B is a subset of event A, the probability of (A and B) is just

the probability of B itself. For instance, in a random draw from a deck of cards, the

probability that the card is a king and the king of spades is the same as the proba-

bility that the card is the king of spades, since the event “king of spades” is a subset

of the event “king.” Therefore, by the rules of conditional probability, the probabil-

ity of drawing the king of spades given that the card is a king equals P(king of

spades and king)/P(king) ⫽ P(king of spades)/P(king) ⫽ (1/52)/(4/52) ⫽ 1/4, which

is quite intuitive. In a similar vein, for Y deﬁned as a count variable limited to

positive values, the event that Y equals any particular value 1, 2, 3, ..., is a subset

of the event that Y is greater than zero. Thus, P(Y ⫽ y 冟Y ⬎ 0) ⫽ P(Y ⫽ y and Y ⬎ 0)/

P(Y ⬎ 0) ⫽ P(Y ⫽ y)/P(Y ⬎ 0).

In the zero-truncated PRM, the density of Y is therefore adjusted by the proba-

bility that Y is a positive count. That is, since P(Y ⫽ 0) ⫽ e

⫺µ

/0! ⫽ exp(⫺µ), the

probability that Y is a positive count is 1 ⫺ exp(⫺µ). Therefore, the density of Y for

the truncated PRM is

f(y

冟y

⬎ 0,x

ββ

)⫽

ᎏ

⫺

)

ᎏ

(10.5)

As before, the likelihood function is formed by making the substitution µ

⫽

exp(冱β

), and taking the product of the densities over the n cases in the sample

(this is left as an exercise for the reader). Grogger and Carson (1991) give the con-

ditional mean and variance of Y for the truncated PRM: The conditional mean is

/(1⫺e

⫺µ

). In that the denominator is less than 1, the truncated mean is larger than

the untruncated mean. The conditional variance is

ᎏ

1⫺

⫺µ

ᎏ

冢

1 ⫺

ᎏ

⫺

⫺µ

ᎏ

冣

Notice that because the term in parentheses is always less than 1, the conditional

variance in the truncated PRM is smaller than the conditional mean; hence equidis-

persion no longer holds for the truncated PRM.

c10.qxd 8/27/2004 2:56 PM Page 362

MODELING COUNT RESPONSES WITH POISSON REGRESSION 363

Example: Number of Lifetime Sex Partners. The column labeled “PRM” in Table

10.2 presents estimates of a truncated PRM for the number of lifetime sex partners

of 357 focal children in the NSFH, as a function of characteristics of both the child

and his or her parents. Predictors include father’s and mother’s education (in years

of schooling attained), a parental monitoring index (interval variable, with higher

scores indicating greater supervision of the child’s activities in wave 1), father’s and

mother’s sexual permissiveness (interval variables, with higher scores indicating

greater sexual permissiveness), the child’s age at ﬁrst intercourse (in years), male (a

dummy for male children), child’s sexual permissiveness (interval variable, with

higher scores indicating greater permissiveness), and the cross-

product of male with child’s sexual permissiveness.

The model is signiﬁcant overall, with a model chi-squared of 767.711

(p ⬍ .0001). The likelihood-ratio index, with a value of .262, suggests that the model

has moderate discriminatory power. In this instance, the model has a control for

diﬀerential exposure. The exposure factor is the log of the number of years of sex-

ual activity, deﬁned as the diﬀerence between the child’s age at the time of the wave

2 survey and the child’s age at initiation of sexual activity. This factor is quite signiﬁ-

cant and positive, as would be expected. Other signiﬁcant factors are the father’s and

mother’s education, the age of the child at ﬁrst intercourse, being male, and the

child’s sexual permissiveness. Interestingly, father’s and mother’s educations have

opposite eﬀects on the average number of partners, with father’s education dimin-

ishing the expected count, and mother’s education raising it. More intuitive are

the results for age at ﬁrst intercourse. Each additional year the child waits before ini-

tiating sex reduces the mean number of partners by 100[exp(⫺ .056) ⫺ 1], or about

Table 10.2 Unstandardized Truncated PRM and NBRM Estimates for the Regression

of Number of Lifetime Sex Partners for Focal Children in the NSFH

Regressor PRM NBRM

Intercept .458 .966

Father’s education ⫺.022* ⫺.021

Mother’s education .045*** .055**

Parental monitoring .125 .013

Father’s sexual permissiveness .002 ⫺.013

Mother’s sexual permissiveness .012 .014

Age at ﬁrst intercourse ⫺.056*** ⫺.101***

Male .517*** .542***

Child’s sexual permissiveness .060*** .071***

Male ⫻ child’s sexual permissiveness ⫺.028 ⫺.019

Exposure .536*** .484***

Overdispersion parameter .391***

Model χ

767.711*** 1109.866***

.262 .379

Equidispersion χ

342.156***

Note: n ⫽ 357.

* p ⬍ .05. ** p ⬍ .01. *** p ⬍ .001.

c10.qxd 8/27/2004 2:56 PM Page 363

ᎏ

%. Males’ expected number of partners is exp(.517) ⫽ 1.677 times greater than

females’. As expected, the more sexually permissive the child, the greater his or her

estimated number of sex partners. This last factor may well be endogenous to the

number of partners. That is, those who have had more partners probably become

more permissive so that their attitudes are consistent with their behavior. As noted

above, the data are probably overdispersed. We address this problem shortly.

Estimated probabilities for the truncated model are calculated by substituting µ

based on the sample regression function, into equation (10.5).

Censoring and Sample Selection

Censored and sample-selected versions of the PRM are similar in principle to the

models discussed in Chapter 9. Censoring from above is a common occurrence with

count data. This applies whenever values of Y above a certain number are all col-

lapsed into one category. For example, the NSFH asks respondents in intimate rela-

tionships how many times they have “hit or thrown things at” a partner in the past

year. Responses are recorded as 0, 1, 2, 3, and 4 or more times. All frequencies above

4 have been recorded as 4, and we therefore have a count variable censored from

above at the value 4. The PRM is readily adjusted for censoring by making the nec-

essary alterations to the likelihood function. Cameron and Trivedi (1998) provide

the details.

Sample selection bias is addressed by assuming that a latent propensity to respond

determines whether or not a count response is observed for the ith case in the sam-

ple. However, all we observe is whether or not a count is recorded for the ith case.

Denote the observed count by Y

and the binary indicator of whether a count is

observed by Y

. The selection model is the probit model for Y

, while the substan-

tive model is the count model for Y

. Selection eﬀects are handled by assuming that

the model for the observed count includes a disturbance term having a bivariate

normal distribution with the disturbance in the probit selection model. This speciﬁ-

cation allows the formation of a likelihood function based on the joint density of Y

and Y

. This full-information technique allows maximum-likelihood estimation of

the parameters of the count model in the presence of selection eﬀects. A two-step

estimator analogous to the Heckman approach discussed in Chapter 9 is also possi-

ble. Cameron and Trivedi (1998) discuss selection models at some length. LIMDEP

allows estimation of count models in the presence of both censoring and sample

selection.

COUNT-DATA MODELS THAT ALLOW FOR OVERDISPERSION

The PRM is typically an inadequate model for count data because such data are usu-

ally overdispersed. In this section we consider some models that are designed to ﬁt

overdispersed data. The ﬁrst is the negative binomial regression model (NBRM). In

the PRM we assumed that the unobserved rate of event occurrence, µ

, for each case

was determined exactly by the regressors. We then assumed that the density of y

was

364 REGRESSION MODELS FOR AN EVENT COUNT

c10.qxd 8/27/2004 2:56 PM Page 364