Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables

Подождите немного. Документ загружается.

Poisson with parameter µ

, and this assumption formed the basis for the likelihood

function. In the NBRM, we relax the assumption that the regressors perfectly deter-

mine the expected event count and allow a disturbance term into the relationship. We

further specify a continuous density for the disturbance term, so that the density of

becomes a mixture of two densities, one discrete and one continuous. The discrete

density is then integrated over the continuous density to produce the NBRM. As we

will see below, this strategy allows the conditional mean and variance of Y to diﬀer.

A second approach to addressing overdispersion is to recognize that this problem

frequently arises because the data observed contain a substantially higher proportion

of zero counts than would be predicted by the PRM. We therefore consider two types

of models that allow for excess zero counts. The zero-inﬂated PRM and NBRM

models make a distinction between zeros that arise probabilistically, in the context

of the PRM or NBRM stochastic process, versus zeros that arise because certain

cases are precluded from having positive counts. In contrast, the hurdle model treats

all cases as being at risk for having positive counts, but allows for the process gen-

erating subsequent counts, given at least one count, to be diﬀerent from the process

that generates positive counts, in general.

Negative Binomial Regression Model

The NBRM arises as a natural consequence of allowing a random disturbance term

in the relationship between the rate of event occurrence (i.e., the conditional mean

of Y

) and the regressors. That is, we model E(Y

) ⫽ θ

⫽ exp[(冱β

) ⫹ ε

]

⫽ exp(冱β

) exp(ε

)

⫽ µ

where υ

⫽ exp(ε

). Observe now that the conditional mean of Y

, θ

, is determined

both by the model covariates, which determine µ

, and by a multiplicative distur-

bance term, υ

. The model regressors, in the form 冱β

, constitute observed

heterogeneity, meaning measured characteristics that induce variation in µ

across

cases. The disturbance term, on the other hand, is a measure of unobserved hetero-

geneity, which as we will see leads to overdispersion in Y. For the NBRM to be iden-

tiﬁed, we must assume that E(υ

) ⫽ 1, in which case E(θ

) ⫽ E(µ

) ⫽ µ

E(υ

) ⫽ µ

(Cameron and Trivedi, 1998; Long, 1997). The density of Y, conditional on the

regressors and υ

, is now

f(y

冟 x

,υ

ββ

) ⫽

ᎏ

⫺

ᎏ

⫽

ᎏ

⫺µ

(

)

ᎏ

. (10.6)

However, since υ

is unobserved, this density cannot be used to construct the likeli-

hood function. (Remember that the only unknowns in the likelihood function must

be the model parameters, not unobservable variables.) The solution is to assume that

has a particular parametric density and then to “integrate it out” of density (10.6)

COUNT-DATA MODELS THAT ALLOW FOR OVERDISPERSION 365

c10.qxd 8/27/2004 2:56 PM Page 365

in order to arrive at the marginal density for Y; that is, the density that is no longer

conditional on υ

. The usual assumption is that υ

has a gamma density with param-

eter α

⫺1

. This is a continuous right-skewed density that resembles a chi-squared

variable. In fact, the chi-squared density is a special case of the gamma density (Hoel

et al., 1971).

Constructing the NBRM Density. “Integrating out” υ

means that we take the aver-

age value of density (10.6) over the distribution of υ

[see Greene (2003) for the

details of the integration]. The advantage of assuming a gamma density for υ

here

is that this integration then has a closed-form solution. The resulting marginal den-

sity of Y

, given the regressors and α, is the negative binomial density (Cameron and

Trivedi, 1998):

f(y

冟 x

ββ

,α) ⫽

ᎏ

⌫(

(

⫺

)⌫

⫹

)

ᎏ

冢

ᎏ

⫺

⫹

ᎏ

冣

⫺1

冢

ᎏ

⫹

⫺1

ᎏ

冣

, (10.7)

where as before, µ

equals exp(冱β

). The gamma function, Γ(⭈), in this expression

is deﬁned by an integral with no closed-form solution (Hoel et al., 1971). However,

it turns out that Γ(a) ⫽ (a ⫺ 1)! if a is an integer. The term α

⫺1

is not typically an

integer. But if it were, given that y

is an integer, density (10.7) would have the same

form as the negative binomial density in expression (10.1), where r ⫽ α

⫺1

and

p ⫽ α

⫺1

/(α

⫺1

⫹ µ

). The product of density (10.7) over all n sample cases is the like-

lihood function, which is then maximized with respect to α and

ββ

to ﬁnd the MLEs.

Because the conditional mean of Y

in density (10.7) is still µ

⫽ exp(冱β

), the

betas still have the same interpretations as given to those in the PRM. (This holds

true for all count models discussed in this chapter.) Estimated probabilities for each

count are calculated by substituting µ

⫽ exp(冱β

) and α

into expression (10.7).

Greene (1998) presents a convenient recursion formula that can be programmed into

LIMDEP for the calculation of these probabilities.

Testing for Overdispersion. The conditional variance of Y

in the NBRM is

⫹ αµ

. The parameter α, called the overdispersion parameter, is always greater

than or equal to zero. This means that the conditional variance is normally greater

than the conditional mean. If α equals zero, the conditional variance is equal to the

conditional mean and the NBRM reduces to the PRM. That is, the PRM is nested

inside the NBRM, and therefore a test for overdispersion is a test for whether α ⫽ 0.

This can be performed using either a nested chi-squared test or a Wald test of the form

z ⫽ α

/σ

. The two tests are asymptotically equivalent (Cameron and Trivedi, 1998).

However, in that α cannot be less than zero, the distribution of these test statistics is

nonstandard. Thus, when performing the chi-squared test at a given level of signiﬁ-

cance, say δ, we use the critical value of 2δ for the test statistic as the criterion. For

the Wald test, we simply use the critical value corresponding to δ rather than δ/2. For

example, performing the chi-squared or Wald test at the .05 level for H

: α ⫽ 0

involves using the critical χ

value corresponding to the .1 level, or the critical z value

corresponding to the .05 level, and so on (Cameron and Trivedi, 1998).

366 REGRESSION MODELS FOR AN EVENT COUNT

c10.qxd 8/27/2004 2:56 PM Page 366

COUNT-DATA MODELS THAT ALLOW FOR OVERDISPERSION 367

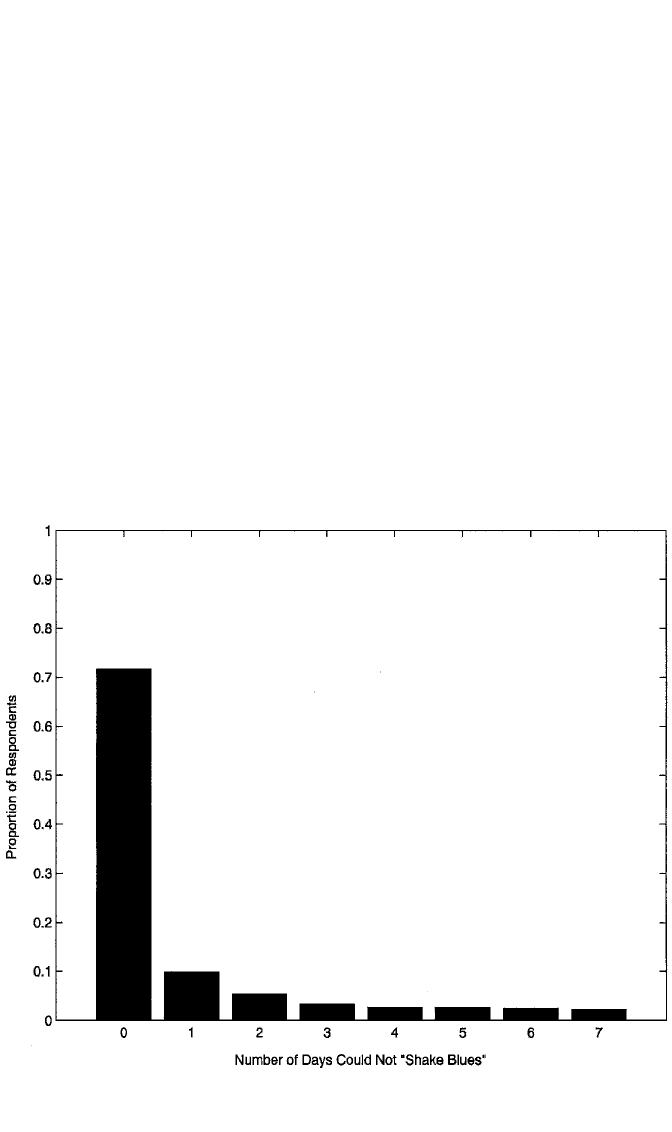
Example: Number of Days of Depression. Figure 10.5 shows the number of days

during the past week on which respondents “could not shake oﬀ the blues, even with

help from your family or friends,” for the 416 main respondents in the couples

dataset. This item is one of 12 similar items that constitute the short form of the

Center for Epidemiological Studies Depression (CESD) scale. Although these items

are typically used in a scale, here I focus simply on a count of the number of days

on which respondents experienced this particular symptom of depression. The vari-

able has a mean of .839 and a variance of 2.926. These values suggest that the data

are overdispersed. We notice also that there is an exceptionally high proportion of

zero counts: 71% of respondents report no days in which they experienced this

symptom. Both phenomena, overdispersion and excess zeros, suggest that the PRM

will not be an appropriate model for these data. One hypothesis of interest with

respect to this variable is that women will tend to be psychologically more adversely

aﬀected by relationship problems than men, or conversely, more psychologically

protected by a good relationship. This is reasonable given that (1) women are social-

ized to be more sensitive to relationship issues than men are, and (2) women tend

to respond to stress more with depressive symptomatology, whereas men tend to

respond more with abuse of drugs and alcohol.

Figure 10.5 Distribution on number of days in the past week respondents could not “shake oﬀ the blues”

for 416 couples in the NSFH.

c10.qxd 8/27/2004 2:56 PM Page 367

368 REGRESSION MODELS FOR AN EVENT COUNT

The PRM estimates for Y ⫽ number of days could not “shake blues” (depression

days, for short), based on several couple characteristics, are shown in the ﬁrst col-

umn of Table 10.3. Predictors not previously described are a dummy variable reﬂec-

ting the male being the main respondent of the face-to-face interview (male main

respondent), the male’s age at inception of the union, the total household income for

the couple, the number of children under 18 in the household, a relationship happi-

ness score (interval variable based on both partners’ reports, ranging from 1 ⫽ “very

unhappy” to 7 ⫽ “very happy”), and the cross-products of male with both open dis-

agreement and relationship happiness. Of particular interest are the eﬀects of open

disagreement and relationship happiness, as well as their interactions with being

male. The model suggests that open disagreement has a signiﬁcant positive eﬀect

on depression days: Each 1-unit increase in disagreements increases mean depres-

sion days by a factor of exp(.934) ⫽ 2.545 for women. For men, each 1-unit increase

in disagreement increases the expected count of depression days by exp(.934 ⫺

.418) ⫽ 1.675. As expected, the impact of disagreement is signiﬁcantly weaker for

men than for women. On the other hand, the eﬀect of happiness in reducing the

mean number of depression days is stronger for men than for women, contrary

to hypothesis. For women, the factor change for unit increases in happiness is

exp(⫺ .095) ⫽ .909, and not signiﬁcant. For men, it is signiﬁcantly greater in mag-

nitude than for women, at exp(⫺ .095 ⫺ .195) ⫽ .748. The results also suggest that a

greater number of children reduces depression days. (The signiﬁcant eﬀect for being

male is not interpretable, since it represents the gender diﬀerence at zero dis-

agreements, a value outside the observed range of this predictor.)

Table 10.3 Unstandardized PRM and NBRM Estimates for the Regression of

Number of Days in the Past Week Respondents Could Not “Shake Oﬀ the Blues”

Regressor PRM NBRM

Intercept ⫺1.271* ⫺1.280

Male main respondent 1.697* 2.195

Male’s age at union inception .006 .007

Union duration .003 .001

Household income ⫺.005 ⫺.004

Number of children ⫺.128* ⫺.109

Open disagreements .934*** .951**

Relationship happiness ⫺.095 ⫺.111

Male ⫻ open disagreements ⫺.418** ⫺.410

Male ⫻ relationship happiness ⫺.195* ⫺.283

Overdispersion parameter 3.438***

Model χ

172.203*** 443.810***

.126 .326

Equidispersion χ

271.607***

Note: n ⫽ 416.

* p ⬍ .05. ** p ⬍ .01. *** p ⬍ .001.

c10.qxd 8/27/2004 2:56 PM Page 368

The second column of the table shows the NBRM estimates. The ﬁrst item of inter-

est is the test for whether the data are overdispersed, which is the test for H

: α⫽ 0. The

value of α is estimated as 3.438. The Wald test statistic, with a z-value of 5.319

(p ⬍ .0001), strongly rejects H

. The nested chi-squared test statistic, shown as

“equidisperion χ

” in the bottom of the table, is a one-degree-of-freedom chi-squared

equal to the diﬀerence in model chi-squareds between the PRM and the NBRM. Its

value is 443.810 ⫺ 172.203 ⫽ 271.607, as shown in the table. With a p-value less than

.0001, this test statistic also results in a sound rejection of the equidispersion hypothe-

sis. We notice now that although the coeﬃcients of the NBRM are comparable in value

with those in the PRM, all are nonsigiﬁcant except for the eﬀect of open disagreement.

The latter suggests that unit increases in open disagreement increase the expected count

of depression days by a factor of exp(.951) ⫽ 2.588, or 159%. Recall that standard

errors for the PRM are downwardly biased in the presence of overdispersion. Hence,

using the appropriate model has resulted in larger standard errors, diminishing the size

of test statistics for the individual coeﬃcients. Although fewer coeﬃcients are sig-

niﬁcant in the NBRM, compared to the PRM, R

has increased substantially. This is

due to the addition of the overdispersion parameter to the likelihood function rather than

to an enhanced ability of the regressors to account for the response.

Truncated NBRM. A truncated version of the NBRM can also be estimated for

data limited to positive counts. Again, the density function for the response is

adjusted by the probability of a positive count. The probability of a zero count in

the NBRM is

f(0 冟x

ββ

,α)⫽

ᎏ

⌫(

(

⫺

)⌫

(

⫹

0 ⫹

ᎏ

冢

ᎏ

⫺

⫹

ᎏ

冣

⫺1

冢

ᎏ

⫹

⫺1

ᎏ

冣

⫽

冢

ᎏ

⫺

⫹

ᎏ

冣

⫺1

⫽(1⫺ αµ

)

⫺α

−1

and therefore the probability of a positive count is

1⫺ (1⫺ αµ

)

⫺ α

−1

The density of the truncated NBRM is

f(y

冟 y

⬎ 0,x

ββ

,α) ⫽

ᎏ

1⫺ (1⫺

αµ

)

⫺

−

ᎏ

⌫(

(

⫺

)⌫

(

⫹

)

ᎏ

冢

ᎏ

⫺

⫹

ᎏ

冣

⫺1

冢

ᎏ

⫹

⫺1

ᎏ

冣

. (10.8)

As always, the product of this density over all n cases is the likelihood function,

which is maximized to ﬁnd the MLEs. Estimated probabilities for each count

are calculated by substituting µ

⫽ exp(冱β

) and α

into expression (10.8). In

untruncated models, employing the PRM with overdispersed data does not interfere

with obtaining consistent estimates of the parameters. However, as Grogger and

Carson (1991) point out, this property does not carry over to truncated data.

Ignoring overdispersion in a truncated response by inappropriately applying the

COUNT-DATA MODELS THAT ALLOW FOR OVERDISPERSION 369

c10.qxd 8/27/2004 2:56 PM Page 369

PRM results in inconsistent parameter estimates, as well as biased estimates of

standard errors.

Lifetime Number of Sex Partners, Revisited. The second column of

Table 10.2 presents the truncated NBRM for the lifetime number of sex partners for

the NSFH focal children. Both the Wald and the nested chi-squared tests for the

overdispersion parameter suggest that the hypothesis of equidispersion should be

rejected. In this case, there is little substantive change in the conclusions except

that the coeﬃcient for father’s education is no longer signiﬁcant. Again, with the

addition of the overdispersion parameter, R

has increased somewhat.

Zero-Inﬂated Models

Zero-inﬂated models, deﬁned by Greene (1994), Lambert (1992), and Long (1997),

among others, account for excess zeros by distinguishing between two diﬀerent

types of zero counts. Borrowing terminology employed for the analysis of contin-

gency tables, I refer to these as structural versus sampling zeros (Agresti, 2002).

Structural zeros come from a population that is not at risk for the events of interest,

often because they are logically precluded from experiencing such events. Sampling

zeros come from a diﬀerent population that is at risk for experiencing events, but

people with zero counts simply have not experienced any events within the domain

of observation, due to the stochastic nature of the event process. As an example, sup-

pose that we were to ask a sample of adolescents: “How many diﬀerent sex partners

have you had in the past month?” Zero counts would arise for two reasons. One pop-

ulation of adolescents has not yet initiated sexual activity and so are logically pre-

cluded from having any sex partners. Their zeros are therefore structural zeros. The

other population has initiated sexual activity, but certain adolescents have just not

engaged in sexual activity with anyone in the past month. Their zeros are sampling

zeros; they are subject to an event process that eventuates in some probability of hav-

ing a zero count. Similarly, our example of the number of days in the previous week

on which respondents could not “shake the blues” can be seen as arising from a

zero-inﬂated event process. Some people are simply not prone to melancholy or

depression because they do not respond in that manner to stress. Other people are

indeed prone to depression but have not experienced any depression days in the past

week. In short, whenever some of the zero counts in a sample can come from a sub-

population of those who for some reason are precluded from experiencing the events

of interest, a zero-inﬂated model may be appropriate.

ZIP Model. The zero-inﬂated Poisson (ZIP) model applies the Poisson model to the

population of those who are at risk for the events in question, and a separate binary

response model to model the probability of being in the structural-zero group. The

probability of a zero count is then a weighted average of the probability that Y ⫽ 0

in each group, where the weights are the probabilities of belonging to each group.

Let P

represent the structural-zero population and P

⫹

represent the population at

risk for at least one event. Also, let ψ

represent the probability that the ith case is in

370 REGRESSION MODELS FOR AN EVENT COUNT

c10.qxd 8/27/2004 2:56 PM Page 370

the structural-zero group, and (1 ⫺ ψ

) represent the probability of being in the at-

risk group. The probability of a zero count, according to the ZIP, is

f(0 冟x

ββ

) ⫽ ψ

P(Y

⫽ 0 冟 P

) ⫹ (1 ⫺ ψ

)P(Y

⫽ 0 冟 P

⫹

)

⫽ ψ

(1) ⫹ (1 ⫺ ψ

) exp(⫺µ

)

⫽ ψ

⫹ (1 ⫺ ψ

) exp(⫺µ

). (10.9)

Notice that the probability of a zero for those in P

is 1. This is referred to as a degen-

erate probability distribution (Cameron and Trivedi, 1998). For Y greater than zero, the

probability of any given count is equal to the probability of being in the at-risk group

times the probability of having that count, given that one is at risk for events:

f(y

冟x

ββ

)⫽ (1 ⫺ ψ

)

ᎏ

⫺

ᎏ

for y

⫽ 1,2,3,..., (10.10)

where µ

⫽ exp(冱β

). Together, expressions (10.9) and (10.10) constitute a density

since the probabilities for Y ⫽ 0,1,2,...sum to 1 (the proof is left as an exercise).

The probability of being in P

, ψ

, is governed by a separate binary response

model. Most often, a logit model is used, in which the covariates are the same as those

in the Poisson model (although they need not be), but the parameters are, of course,

diﬀerent. Assuming the regressors are the same in both models, the model for ψ

ᎏ

1 ⫺

ᎏ

⫽

冱

. (10.11)

The ZIP model formulated in this way requires twice as many parameters as the

PRM. Lambert (1992) suggested that if the same covariates aﬀect both ψ

and µ

,it

would be natural to reduce the number of parameters by formulating ψ

as a function

of µ

. However, I agree with Long (1997, pp. 243–244) that “...it is diﬃcult to

imagine a social science application in which one would expect the parameters in the

binary process to be a simple multiple of the parameters in the Poisson process.”

Therefore, I do not cover this more simplistic model here. The interested reader is

referred to Lambert (1992) for that coverage.

Estimation. Estimation of the ZIP model proceeds by maximizing the ZIP likeli-

hood function with respect to the parameters [Cameron and Trivedi (1998) present

the log-likelihood function for the model]. Estimated probabilities for counts under

the ZIP model are calculated by employing the MLEs to construct ψ

and µ

and then

inserting these terms into expressions (10.9) and (10.10) to recover the probabilities.

The appropriate formulas are

ψˆ

⫽

ᎏ

1⫹

冢

冱

冢冱

冣

ᎏ

(10.12)

⫽ exp

冢

冱

ik冣

. (10.13)

COUNT-DATA MODELS THAT ALLOW FOR OVERDISPERSION 371

c10.qxd 8/27/2004 2:56 PM Page 371

The conditional mean and variance of Y in the ZIP model are (Long, 1997)

E(Y

冟x

) ⫽ (1 ⫺ ψ

)µ

V(Y

冟x

) ⫽ (1 ⫺ ψ

)(µ

⫹ ψ

In that µ

⫹ ψ

is greater than µ

unless ψ

⫽ 0, the conditional variance exceeds the

conditional mean, and overdispersion is therefore accommodated.

Comparing PRM and ZIP Models. There is no nested chi-squared test for com-

paring the ZIP and PRM because the PRM is not nested inside the ZIP. In order for

the PRM to be nested within the ZIP, ψ

would have to equal zero, in which case the

ZIP would reduce to the PRM. However, there is no simple set of parameter con-

straints that can achieve this result. The natural constraint would be to set

γγ

⫽ 0 in

equation (10.11). However, under this condition ψ

is exp(0)/[1 ⫹ exp(0)] ⫽

ᎏ

, which

is not the desired result. In light of this, we can employ a test proposed

by Vuong (1989) that compares nonnested models. Let f

( y

冟x

) be the predicted

probability that Y

⫽ y

for the ith case under model 1, with x

that case’s vector of

regressor values, and let f

( y

冟x

) be the predicted probability under model 2.

Furthermore, let

⫽ ln

ᎏ

(

冟

)

ᎏ

and let the mean and standard deviation of m

over all n cases be m

苶

and s

, respec-

tively. Then the Vuong test statistic for testing model 1 against model 2 is

V ⫽

ᎏ

苶

兹n

苶

ᎏ

which is asymptotically distributed as standard normal. If model 1 is the ZIP and

model 2 is the PRM, the ZIP is favored if V is greater than 1.96, whereas the PRM

is favored if V is less than ⫺1.96.

ZINB Model. The zero-inﬂated negative binomial (ZINB) model is developed in a

comparable manner to the ZIP. For the NBRM, the probability of a zero count is

(1 ⫺ αµ

)

⫺␣

⫺1

. Therefore, the ZINB model for the zero and positive counts is

f(0 冟 x

ββ

) ⫽ ψ

⫹ (1⫺ψ

)(1 ⫺ αµ

)

⫺␣

⫺1

f(y

冟 x

ββ

,α)⫽ (1⫺ψ

)

ᎏ

⌫(

(

⫺

)⌫

⫹

)

ᎏ

冢

ᎏ

⫺

⫹

ᎏ

冣

⫺1

冢

ᎏ

⫹

⫺1

ᎏ

冣

for y

⫽ 1, 2, 3, ...,

where ψ

, as in the ZIP, is determined by a logit model with a separate parameter set.

These densities are used to construct the likelihood function to obtain the MLEs. As

usual, plugging ψ

, µ

, and α

into these expressions provides predicted probabilities

for each count, where ψ

and µ

are estimated according to equations (10.12) and

372 REGRESSION MODELS FOR AN EVENT COUNT

c10.qxd 8/27/2004 2:56 PM Page 372

COUNT-DATA MODELS THAT ALLOW FOR OVERDISPERSION 373

(10.13), based on the MLEs for the ZINB model. The conditional mean and variance

for the ZINB model are (Long, 1997)

E(Y

冟x

) ⫽ (1 ⫺ ψ

)µ

V(Y

冟x

) ⫽ (1 ⫺ ψ

)µ

[1 ⫹ µ

(ψ

⫹ α)].

Once again, it is evident that the conditional variance exceeds the conditional mean. The

ZIP is nested inside the ZINB, so a nested chi-squared test can help choose between

these models. However, the NBRM is not nested inside the ZINB model, so again, the

Vuong statistic can be used to compare them, as in the case for the ZIP and PRM.

Depression Days, Continued. Table 10.4 presents both ZIP and ZINB models for the

number of days respondents could not “shake the blues.” Two columns are shown for

each model. The logit column displays parameter estimates for the logistic regression

of whether a case is a structural zero, while the PRM and NBRM columns provide

the estimates for the relevant count models for those at risk for days of depression.

The reader should notice that the logit and count-model coeﬃcients are generally of

opposite signs. This is sensible, since attributes that reduce the likelihood of being in

the structural-zero group tend to enhance the expected event count, and vice versa. In

the ZIP, the only factor that predicts being in the structural-zero group is open dis-

agreement, with more disagreements reducing the likelihood of being in this group.

The PRM for those with positive counts suggests, again, that disagreements have a

Table 10.4 Unstandardized ZIP and ZINB Estimates for the Regression of Number

of Days in the Past Week Respondents Could Not “Shake Oﬀ the Blues”

ZIP ZINB

Regressor Logit PRM Logit NBRM

Intercept .551 ⫺.103 .216 ⫺.461

Male main respondent ⫺.202 1.773* ⫺.083 1.900

Male’s age at union inception ⫺.001 .007 ⫺.002 .009

Union duration ⫺.001 .001 ⫺.001 .002

Household income ⫺.002 ⫺.006* ⫺.002 ⫺.007

Number of children .151 ⫺.023 .167 ⫺.012

Open disagreements ⫺.901** .484*** ⫺.877* .556**

Relationship happiness .260 .005 .272 .014

Male ⫻ open disagreements .072 ⫺.459* ⫺.050 ⫺.550

Male ⫻ relationship happiness .112 ⫺.127 .142 ⫺.111

Overdispersion parameter .278

Model χ

471.786*** 480.358***

.347 .353

Equidispersion χ

8.572**

Vuong statistic 16.144*** 5.828***

Note: n ⫽ 416.

* p ⬍ .05. ** p ⬍ .01. *** p ⬍ .001.

c10.qxd 8/27/2004 2:56 PM Page 373

374 REGRESSION MODELS FOR AN EVENT COUNT

stronger positive eﬀect on the expected event count for women than for men, as

hypothesized. Additionally, those with a higher household income have signiﬁcantly

fewer expected depression days, net of other eﬀects. The Vuong statistic, with a

value of 16.144, strongly suggests that the ZIP is an improvement over the ordinary

PRM. R

suggests that the ZIP has moderate discriminatory power.

The ZINB model, on the other hand, suggests that open disagreement constitutes

the only factor that aﬀects either the likelihood of being in the structural-zero group,

or the expected event count, given that one is at risk for depression days. The Vuong

statistic for the ZINB versus the ordinary NBRM, at 5.828, indicates that the ZINB is

to be preferred. Whether the ZINB is to be preferred to the ZIP is not quite as straight-

forward. The equidispersion χ

is signiﬁcant, but the Wald test for the dispersion

parameter is not. As these tests are asymptotically equivalent, they should agree; how-

ever, at times there will be such disparities. The safest conclusion is that although

there is some evidence that disagreement has a stronger eﬀect on depression days for

women than men, the only robust eﬀect is that open disagreement raises both the risk

for depression days and the expected count of depression days, net of other factors.

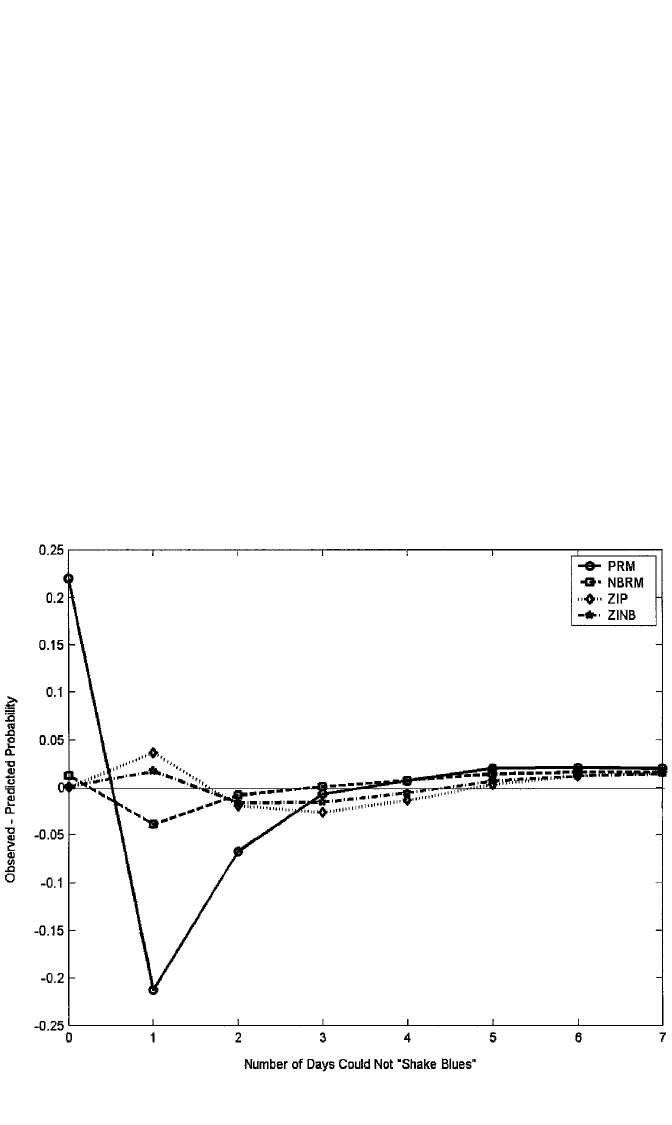
Figure 10.6 illustrates another means of comparing all four models investigated

for depression days, as suggested by Long (1997). It shows a plot of observed minus

predicted probabilities for the PRM, NBRM, ZIP, and ZINB models of depression

Figure 10.6 Observed–predicted probabilities for number of days could not “shake blues,” based on

PRM, NBRM, ZIP, and ZINB models.

c10.qxd 8/27/2004 2:56 PM Page 374