Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables

Подождите немного. Документ загружается.

in equations (11.7) and (11.8), and inserting both into equation (11.6), the log-

likelihood function for the exponential model is:

ln L(

ββ

t,x) ⫽



i⫽1

ln{exp[y

⫺ x

⬘

ββ

⫺ exp(y

⫺ x

⬘

ββ

)]}

⫹ (1 ⫺ c

) ln{exp[⫺exp(y

⫺ x

⬘

ββ

)]}),

which after some algebraic manipulation reduces to

ln L(

ββ

t,x) ⫽



i⫽1

⫺ x

⬘

ββ

) ⫺ exp(y

⫺ x

⬘

ββ

)]

(11.10)

As always, maximizing function (11.10) with respect to

ββ

provides MLEs for the

elements in

ββ

. As the focus of this chapter is on the Cox model, discussed below, I

postpone discussion of inferences until that section. However, the usual test statis-

tics based on MLEs are applicable, including likelihood-ratio tests for the model as

a whole, chi-squared diﬀerence tests for nested models, and Wald chi-squared tests

for individual coeﬃcients. These are similar in form to those for other likelihood-

based models discussed in Chapters 7 to 10.

Application to Union Disruption. Model 1 in Table 11.2 presents the results of

estimating the exponential model for the log of survival time in 1230 married and

unmarried cohabiting unions in the NSFH. Several covariates that have been

REGRESSION MODELS IN SURVIVAL ANALYSIS 395

Table 11.2 Parametric and Semiparametric Regression Models for the Hazard

of Union Disruption

Predictor Model 1

Model 2

Model 3

Model 4

Model 5

Intercept 1.917***

Relationship duration (months) .029*** ⫺.028*** ⫺.021*** ⫺.028*** ⫺.022***

Female’s age at union .054*** ⫺.053*** ⫺.053*** ⫺.074*** ⫺.055***

Both in a ﬁrst union .792*** ⫺.779*** ⫺.779*** ⫺.479*** ⫺.621***

Alcohol or drug problem ⫺.376* .360* .373* .363* .368*

Open disagreement ⫺.030* .029* .030* .031* .031*

Conﬂict resolution style .233*** ⫺.228*** ⫺.229*** ⫺.184*** ⫺.190***

Continuously cohabiting 1.193*** 1.540***

Cohabiting to married ⫺.159 .321

Union birth ⫺1.457*** ⫺.557***

Note: n ⫽ 1230.

Exponential model.

Cox model.

Cox model adjusted for left truncation.

Cox model adjusted for left truncation, with cohabiting to married and union birth treated as time invariant.

Cox model adjusted for left truncation, with cohabiting to married and union birth as time-varying

covariates.

* p ⬍ .05. ** p ⬍ .01. *** p ⬍ .001.

c11.qxd 8/27/2004 2:56 PM Page 395

shown in past research to aﬀect relationship dissolution are included. All

covariates employed in models 1 to 3 were measured in the ﬁrst wave of the

survey and are fairly self-explanatory. Relationship duration in months taps the

number of months from inception of the union (whether marital or cohabiting)

until the date of the wave 1 interview. Female’s age at union is a proxy for the

couple’s age at inception of the union, since partners’ ages are highly correlated.

Both in a ﬁrst union is a dummy ﬂagging couples in which neither partner has

married or formed a cohabiting union before. Alcohol or drug problem is a

dummy that identiﬁes couples in which either partner has an alcohol or drug

problem. Open disagreement is the frequency of open disagreements in the

relationship over the past year, a continuous variable ranging from 6 to 31.2.

Conﬂict resolution style is also a continuous variable, ranging from 2 to 10,

tapping the extent to which disagreements have been calm and partners have

avoided arguing heatedly or shouting.

Interpreting the Exponential Model. As is evident, all variables are signiﬁcant pre-

dictors of survival time, with longer survival times evidenced by couples who had

been together longer before wave 1, who were older when entering the union, who

were in a ﬁrst union, and who had calmer conﬂict resolution styles. Predictably, cou-

ples in which either partner had an alcohol or drug problem or those with more fre-

quent disagreements had shorter survival times. It is straightforward to generate

predicted survival times using the model. For example, consider a couple together

for two years at wave 1, in which the woman was 21 at the start of the union, who

were both in a ﬁrst union, who had no substance abuse problems, whose open dis-

agreement score was 10, and whose conﬂict resolution score was 5. Their predicted

log-survival time in months is

ln T

⫽1.917 ⫹ .029(24) ⫹ .054(21) ⫹ .792 ⫺ .030(10) ⫹ .233(5) ⫽ 5.404,

which implies a survival time of 222.3 months, about 18

ᎏ

years.

Of perhaps more importance are the interpretations of the eﬀects. Each coeﬃcient

represents the estimated additive change in log-survival time for a 1-unit increase in

the relevant predictor, net of other covariates. Or, exponentiating the coeﬃcient gives

us the acceleration or deceleration in survival time for a 1-unit increase in the pre-

dictor. Hence, each year older the woman is before entering a union magniﬁes sur-

vival time by a factor of exp(.054) ⫽ 1.055, or 5.5%. Similarly, those with substance

abuse problems are estimated to have survival times that are lower by a factor of .687

compared to others. Or, their survival times are estimated to be reduced by about

31.3%. A convenient feature of the exponential model is that if the sign of the

coeﬃcient is reversed, we get the eﬀect on the log of the hazard. This makes perfect

intuitive sense, since a greater hazard of event occurrence should shorten survival

time, and vice versa. Thus, the eﬀect of relationship duration on the log hazard is

⫺.029, while the eﬀect of alcohol or drug problems is .376. Exponentiating these

coeﬃcients provides us with an estimate of the hazard ratio—the ratio of hazards—

for those who are 1 unit apart on the relevant predictor. As an example, the hazard

396 INTRODUCTION TO SURVIVAL ANALYSIS

c11.qxd 8/27/2004 2:56 PM Page 396

ratio for those with alcohol or drug problems versus others is exp(.376) ⫽ 1.456. Or,

the hazard of disruption for couples with substance abuse problems is elevated by

about 46%.

Cox Regression Model

One problem with parametric models is that their accuracy depends very much on

whether the correct distribution is selected, and selection of the correct distribu-

tion, unless guided by strong theory, can be a challenging task. Recall that an

exploration of the parametric form of the survival-time distribution for the union

disruption problem using the techniques enumerated above failed to identify a sin-

gle distribution as best. The exponential distribution was chosen for simplicity. But

during model estimation a Lagrange multiplier chi-squared test for the constraint

on σ (not shown) resulted in rejection of the null hypothesis that σ ⫽ 1. As the

value of σ

is 1.216, there is evidence that the hazard of union disruption is declin-

ing over time. (However, a declining hazard can also be an artifact of unmeasured

heterogeneity, as explained in Chapter 12.) This suggests that the Weibull model

may be more appropriate, although there is no guarantee that it is the correct dis-

tribution, either.

In a highly inﬂuential 1972 paper, the statistician D. R. Cox proposed a model and

associated estimation technique that obviates the need to identify the appropriate dis-

tribution for survival time. Known widely as the proportional hazards model, this tool

has come to dominate survival analysis in many ﬁelds. Although this technique has

some drawbacks, its major advantage is that the researcher can be completely

indiﬀerent to the form of the survival-time distribution and still obtain good estimates

of covariate eﬀects. The estimation technique is called partial likelihood estimation

and represents a rather remarkable insight on Cox’s part. For this reason, it is worth

considering in some detail.

Model and Its Interpretation. First, the Cox model takes the form

(t) ⫽ h

(t) exp(x

⬘

ββ

), (11.11)

where h

(t) is the hazard of event occurrence at time t for the ith case. Note here that

the covariate vector, x, and parameter vector,

ββ

, include only the explanatory vari-

ables; there is no constant term in either. The term h

(t) is a baseline hazard function

that is left unspeciﬁed as to form. It is interpreted as the hazard function for a case

whose covariate values are all zero. “Left unspeciﬁed” essentially means just that:

We do not give it any particular form in the model. It could potentially represent any

of the parametric survival-time functions discussed so far, as well as any number of

others. As we will see, this function can be safely ignored in the estimation of the

parameters. Covariates have the eﬀect of raising or lowering the hazard from the

baseline by some ﬁxed amount. Moreover, exp(β

) represents the ratio of hazards for

people who are a unit apart on X

, controlling for other eﬀects. For example, suppose

REGRESSION MODELS IN SURVIVAL ANALYSIS 397

c11.qxd 8/27/2004 2:56 PM Page 397

that there are two covariates in the model, X

and X

. Further, consider the ratio of

the hazards for individuals i and j who are 1 unit apart on X

, controlling for X

. We

have

⫽⫽exp(β

This means that the hazard for individual i is exp(β

) times the hazard for individual

j at any given time, or their hazards are proportional—with proportionality constant

exp(β

)—over time. Formally, a proportional hazards model is one in which “the

hazard for any individual is a ﬁxed proportion of the hazard for any other individ-

ual” over time (Allison, 1995, p. 114). Despite this property giving the model its

name, it is easy to modify the model to handle nonproportionality, as I show below.

The model in log-hazard form is

ln[h

(t)] ⫽ λ

(t) ⫹ x

⬘

ββ

where λ

(t) ⫽ ln[h

(t)].

Partial Likelihood Estimation. According to Blossfeld et al. (1989), the likelihood

function for equation (11.11) can be factored into the product of separate terms as

follows. First, suppose that k of the n people in the sample are uncensored. We then

order the k event times such that t(1) ⬍ t(2) ⬍

...

⬍ t(k), where the notation “t(i)”

represents the ith ordered event time. Additionally, let R(t(i)) denote the risk set at

the ith ordered event time. As before, the risk set consists of all cases with survival

or censored times greater than or equal to t(i). Then the likelihood function for the

Cox model is

ββ

(t)  t,x) ⫽



i⫽1

o∈R(t(i))



(t(i)) exp(x

⬘

ββ

)



i⫽1

)

exp(x

⬘

ββ

)

where S

) is the baseline survival function for the ith case. Cox termed the ﬁrst fac-

tor the partial likelihood and treated it like an ordinary likelihood, while discarding

the remaining terms. Thus, the partial likelihood (PL) function is

PL(

ββ

t,x) ⫽



i⫽1

. (11.12)

Cox proposed maximizing function (11.12) with respect to

ββ

to arrive at the param-

eter estimates. Because this approach discards information about

ββ

contained in

the other terms in the likelihood function, the PL estimator is not fully eﬃcient.

However, the estimator still possesses the other desirable characteristics of ML esti-

mation, such as consistency and asymptotic normality (Klein and Moeschberger,

1997).

exp(x

⬘

ββ

)

ᎏᎏ

ο∈R(t(i))

 exp(x

⬘

ββ

)

exp(x

⬘

ββ

)

ᎏᎏ

ο∈R(t(i))

 exp(x

⬘

ββ

)

(t) exp[β

⫹ 1)] exp(β

)

ᎏᎏᎏᎏ

(t) exp(β

) exp(β

)

(t)

ᎏ

(t)

398 INTRODUCTION TO SURVIVAL ANALYSIS

c11.qxd 8/27/2004 2:56 PM Page 398

Understanding the Partial Likelihood. Let’s take a closer look at function (11.12)

in order to understand what the terms inside the product operator represent. Each

term is based on an application of conditional probability rules to the probability of

an event at time t(i). In particular, we ask: What is the “probability” that a person

with covariate vector x

“fails” at time t(i) given that there is one failure at time t(i)?

In that time is continuous, we are dealing with hazards instead of probabilities, but

the rules are the same. We have

P(case x

fails at t(i)  one failure at t(i))

⫽⫽

(11.13)

It should be clear that the numerator of expression (11.13) is the hazard for the case

that fails at t(i) and the denominator is the sum of the hazards for all those at risk at

t(i). As is evident here, the baseline hazard function cancels out of the numerator and

denominator of expression (11.13) and can therefore be ignored. Finally, to see how

function (11.12) is applied in practice, we take a very simpliﬁed example. Suppose

that the sample consists of three observations on marital unions having survival

times of 42, 56, and 86 months. The ﬁrst two times are disruption times, while the

last is a censored survival time. Further, assume there is only one covariate, X

, in the

model. The PL function for these three observations is (where subscripts represent

the case numbers)

PL(

ββ

t,x) ⫽ .

As is evident, censored observations (e.g., the third observation here) contribute only

to the denominators in the partial likelihood, not to the numerators. In general, there

are as many separate terms in this product as there are uncensored cases.

Advantages and disadvantages of PL. Several comments are in order about the PL

technique. First, the PL function only employs information about the ordering of event

times, not the times themselves. It is therefore not necessary that these times be meas-

ured precisely, as long as we are able to order them from smallest to largest. On the

other hand, tied event times pose a problem, since the function assumes that the event

times are distinct. Hosmer and Lemeshow (1999) discuss a handful of techniques that

have been developed to handle ties, and these are implemented in mainstream software,

such as SAS. An exact partial likelihood in the presence of ties is given in Kalbﬂeisch

and Prentice (1980), whereas approximations to the exact likelihood have been devel-

oped by Breslow (1974) and Efron (1977). As the exact function requires longer

exp(βX

)

ᎏᎏᎏ

exp(βX

) ⫹ exp(βX

)

exp(βX

)

ᎏᎏᎏᎏ

exp(βX

) ⫹ exp(βX

)

exp(x

⬘

ββ

)

ᎏᎏ

ο∈R(t(i))



exp(x

⬘

ββ

)

(t) exp(x

⬘

ββ

)

ᎏᎏᎏ

o∈R(t(i))



(t) exp(x

⬘

ββ

)

P(case x

fails at t(i))

ᎏᎏᎏ

P(one failure at t(i))

P(case x

fails at t(i) 傽 one failure at t(i)

ᎏ

ᎏᎏᎏᎏᎏᎏ

P(one failure at t(i))

REGRESSION MODELS IN SURVIVAL ANALYSIS 399

c11.qxd 8/27/2004 2:56 PM Page 399

computing time than either approximation, the latter have been viewed as more

advantageous in application. However, given the rapid evolution of ever-speedier

processors, the issue of computer time may ultimately diminish in importance. Of

the two approximations, Efron’s is recommended as being closer to the exact method

(Hosmer and Lemeshow, 1999). Nevertheless, if there are too many tied survival

times in one’s data—say more than 5% of the observations are tied at any given

time—the discrete-time techniques discussed in Chapter 12 should be considered

(Yamaguchi, 1991).

Inferences for the Cox Model. Inferences for the Cox model are performed with

tests that parallel the usual procedures for models estimated with maximum likeli-

hood. First there is a likelihood-ratio test for the signiﬁcance of the model as a

whole. [Actually, Hosmer and Lemeshow (1999, p. 98) refer to the test as a “partial

likelihood-ratio test,” but I will use “likelihood-ratio test” for short.] The null hypoth-

esis for the test is H

: β

⫽ β

⫽

...

⫽ β

⫽ 0 versus H

: at least one β

is not zero.

The test statistic is the likelihood-ratio chi-squared (LRχ

LRχ

⫽⫺2 ln

ᎏ

⫽⫺2 ln L

⫺ (⫺2lnL

where L

is the partial likelihood for a model with no covariates and L

is the partial

likelihood for the hypothesized model, evaluated at the partial-likelihood estimates

(PLEs) of the parameters. Under the conditions that the sample size is large—in

particular, that the number of uncensored cases is large (Hosmer and Lemeshow,

1999)—and the null hypothesis is true, this statistic is approximately distributed as

chi-squared with K degrees of freedom. Also, there are LRχ

tests for nested mod-

els. If model B is nested inside model A, a test for the constraints on A leading to B

is ∆χ

⫽ LRχ

(A) ⫺ LRχ

(B). If the constraints are valid, ∆χ

has a chi-squared dis-

tribution with degrees of freedom equal to the number of constraints imposed (e.g.,

the number of parameters set to zero). As PL estimates are asymptotically normally

distributed (Cox, 1975), tests for individual coeﬃcients, referred to as Wald tests,

take the form

Wald χ

⫽



ᎏ



which are one-degree-of-freedom chi-squared tests under the hypothesis that β

⫽ 0.

Finally, conﬁdence intervals for the β

, as well as the hazard ratios, exp(β

), can be

constructed using the standard errors of the coeﬃcients, denoted σ

, and the critical

values of the standard normal distribution. For example, a 95% conﬁdence interval

for β

takes the form b

⫾ 1.96σ

. Exponentiating the lower and upper limits of this

interval provides a 95% conﬁdence interval for exp(β

Cox Models for Union Disruption. Model 2 in Table 11.2 shows the results of esti-

mating the Cox model for the log hazard of union disruption. As mentioned, there is

400 INTRODUCTION TO SURVIVAL ANALYSIS

c11.qxd 8/27/2004 2:56 PM Page 400

no intercept in the model. The LRχ

statistic for the model as a whole is 166.826,

which with six degrees of freedom is highly signiﬁcant (p ⬍ .0001). The coeﬃcients

are quite close in magnitude to those of the exponential model, but opposite in sign,

since we are modeling the log hazard rather than log survival time. As with the expo-

nential model, exponentiating a coeﬃcient provides an estimate of the hazard ratio

for a unit diﬀerence on that predictor, net of other model covariates. Thus, being in

a ﬁrst union is associated with a hazard ratio of exp(⫺.779) ⫽ .459, meaning that

ﬁrst unions have about a 54% lower hazard of union disruption at any given time

compared to others. In a similar vein, exponentiating the coeﬃcient for alcohol or

drug problem suggests that relationships characterized by substance abuse have a

43% higher risk of union disruption at any given time. The standard error for alco-

hol or drug problem is .164. So a 95% conﬁdence interval for the coeﬃcient is

.36 ⫾ 1.96(.164) ⫽ (.039, .681). Or a 95% conﬁdence interval for the ratio of hazards

for those with, versus without, substance abuse problems is [exp(.039), exp(.681)] ⫽

(1.040, 1.976). Note that the coeﬃcients for model 2 cannot be employed to arrive at

an estimator of a given couple’s hazard of disruption. The reason is that an estimator

of the baseline hazard function is missing in Cox models. However, we can estimate

the impact on the hazard associated with given covariates. As indicated below, we can

also use the estimates to construct estimated survival functions.

Adjusting for Left Truncation

As noted above, the sample of unions is characterized by various degrees of left trun-

cation. Left truncation, also referred to as delayed entry into the risk set (Hosmer and

Lemeshow, 1999) or interrupted spells (Hamerle, 1991), represents a form of sam-

ple selectivity. In that left-truncated cases have survived long enough to come under

observation, they tend to overrepresent low-risk cases among any given cohort. This

phenomenon can lead to a loss of estimator eﬃciency or even to biased estimates if

uncorrected (Hamerle, 1991). Programs for AFT models typically do not allow

adjustments for left truncation. But the Cox model is easily accommodated to left-

truncated data, provided that inception of risk is known for each case, as is true of

the current data. Essentially, the partial likelihood function is made conditional on

having survived until the start time of the study [see Guo (1993) and Hamerle (1991)

for technical details]. In SAS’s Cox regression program, PHREG, left-truncated

cases can be speciﬁed via the ENTRYTIME option on the model statement, as well

as in other ways (see Allison, 1995). Model 3 in Table 11.2 shows the estimates for

union disruption after adjusting for left truncation. There is little change in the

coeﬃcients, probably because of the prior restriction that at the beginning of obser-

vation (wave 1), couples had been together for no longer than three years. Left trun-

cation is therefore not as extensive a problem here as it was in the full study [see

DeMaris (2000) for details].

Another Nonparametric Estimator of S( t). The Cox model can also be used to

obtain a nonparametric estimator of the survival function in the presence of left trun-

cation. This provides an alternative estimator to the standard life-table approach

REGRESSION MODELS IN SURVIVAL ANALYSIS 401

c11.qxd 8/27/2004 2:56 PM Page 401

oﬀered by, say, SAS’s procedure LIFETEST, which does not allow such adjustments.

The procedure is to estimate the Cox model without any covariates, using the ENTRY-

TIME option. The result is an alternative nonparametric estimator known as the

Kaplan–Meier estimator. This estimator is particularly desirable when there are few

tied survival times, because it is based on the exact event and censoring times in the

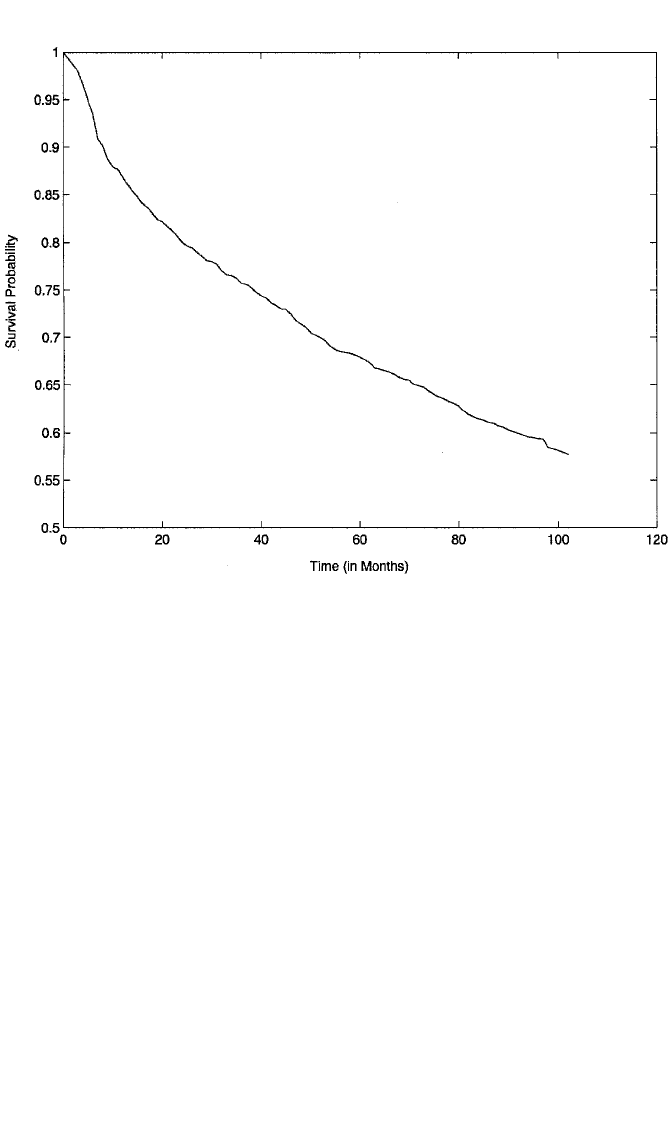
data (Blossfeld et al., 1989). Figure 11.4 shows the nonparametric survival curve—

ignoring the covariates—for the union disruption data using this approach.

Estimating Survival Functions in Cox Regression

One drawback to the Cox model is that there is no simple means for recovering the

estimated survival function, since information about the survival times themselves is

discarded in the estimation process. However, techniques have been developed for

estimating the baseline survival function, S

(t), based on the partial likelihood

parameter estimates. One method, according to Klein and Moeschberger (1997), is

based on the cumulative baseline hazard rate at time t, denoted H

(t), which is a sort

of cumulative sum of the hazards up to time t for all cases at risk. Once b, the vec-

tor of parameter estimates, is obtained by maximizing the PL likelihood, an estimate

402 INTRODUCTION TO SURVIVAL ANALYSIS

Figure 11.4 Kaplan–Meier estimator of survival function for event of union disruption, adjusted for left

truncation.

c11.qxd 8/27/2004 2:56 PM Page 402

of H

(t) can be constructed. The baseline survivor function is then recovered via the

formula S

(t) ⫽ exp[⫺ H

(t)]. Estimated survival functions at given values of the

covariates can then be calculated as

(t  x ⫽ x

) ⫽ S

(t)

exp(x

⬘b)

(11.14)

where x

is a given setting of the covariates.

Figure 11.5 presents separate estimated survival functions for those in ﬁrst unions

and those with prior union histories, based on model 3 in Table 11.2. These functions

are produced using the BASELINE statement in SAS’s PHREG program. This feature

estimates baseline survival functions and then applies equation (11.14) to produce sep-

arate survival curves for those in ﬁrst unions versus others. The other model covariates

are set to their mean values. The ﬁgure conveys quite forcefully that those in ﬁrst unions

have greater survival rates at any given time. For example, 83.5% of ﬁrst unions are

estimated to be intact after ﬁve years, compared with 68.5% of those with a prior union

history; and 76.1% of ﬁrst unions are predicted to survive for at least 102 months (8

ᎏ

years), as opposed to 55.4% of those with a prior union history. The model, of course,

creates these eﬀects since the risk of union disruption is ﬁxed at being 54% lower for

REGRESSION MODELS IN SURVIVAL ANALYSIS 403

Figure 11.5 Survival curves for event of union disruption by whether in a ﬁrst union.

c11.qxd 8/27/2004 2:56 PM Page 403

those in ﬁrst unions. The reader may notice the appearance of an increasing gap

between the survival probabilities of the two groups over time. However, this is just an

artifact of the nonlinear transformation from log-hazards to survival rates rather than a

diﬀerential eﬀect of ﬁrst-union status over time. In model 3, the eﬀects of all covariates

on the log hazard, including ﬁrst-union status, are posited to be constant over time.

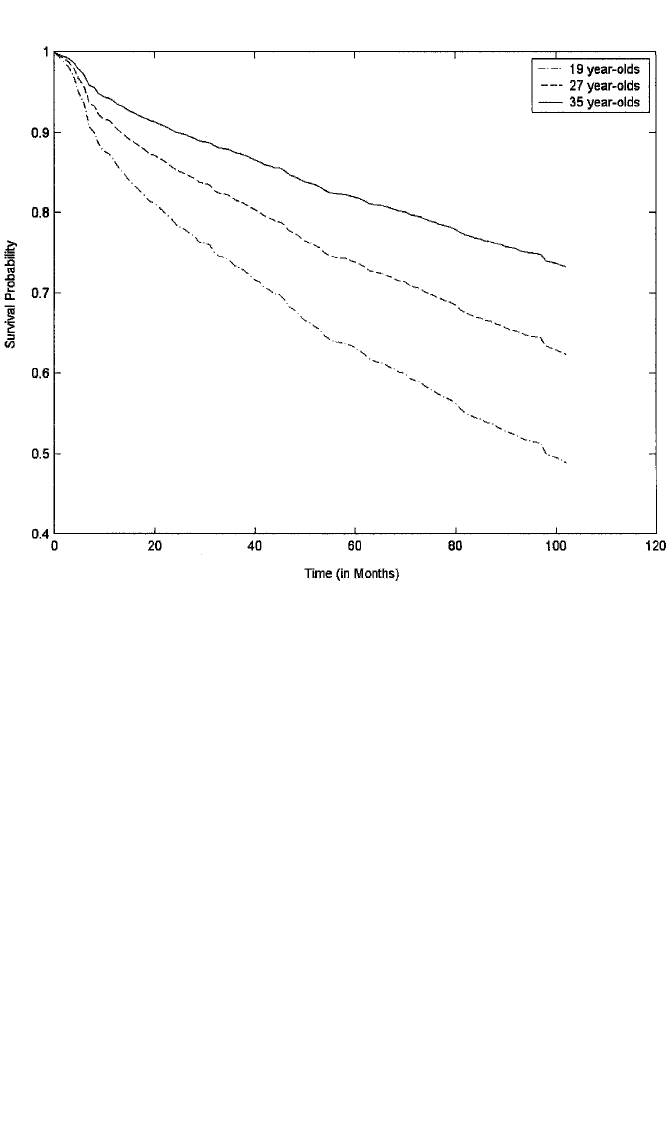
Figure 11.6 shows the eﬀect of age at union formation on survival rates, with other

covariates (including ﬁrst-union status) set to their means. Separate survival curves

are shown for three values for female’s age at union: 19, 27, and 35. Again, the curves

reveal the advantage in being older when forming a union: the survival probabilities

for the three groups at ﬁve years are .632, .739, and .819, respectively.

Time-Varying Covariates

An advantage of the Cox model, and of survival analysis in general, is the ability to

incorporate into the model predictor variables whose values vary over time. Called

time-varying covariates, such explanatory variables are often a natural outcome of

following cases over time. Many personal characteristics change over time, such as

employment status, annual salary, marital status, number of children borne, whether

404 INTRODUCTION TO SURVIVAL ANALYSIS

Figure 11.6 Survival curves for event of union disruption by female’s age at union.

c11.qxd 8/27/2004 2:56 PM Page 404