Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables

Подождите немного. Документ загружается.

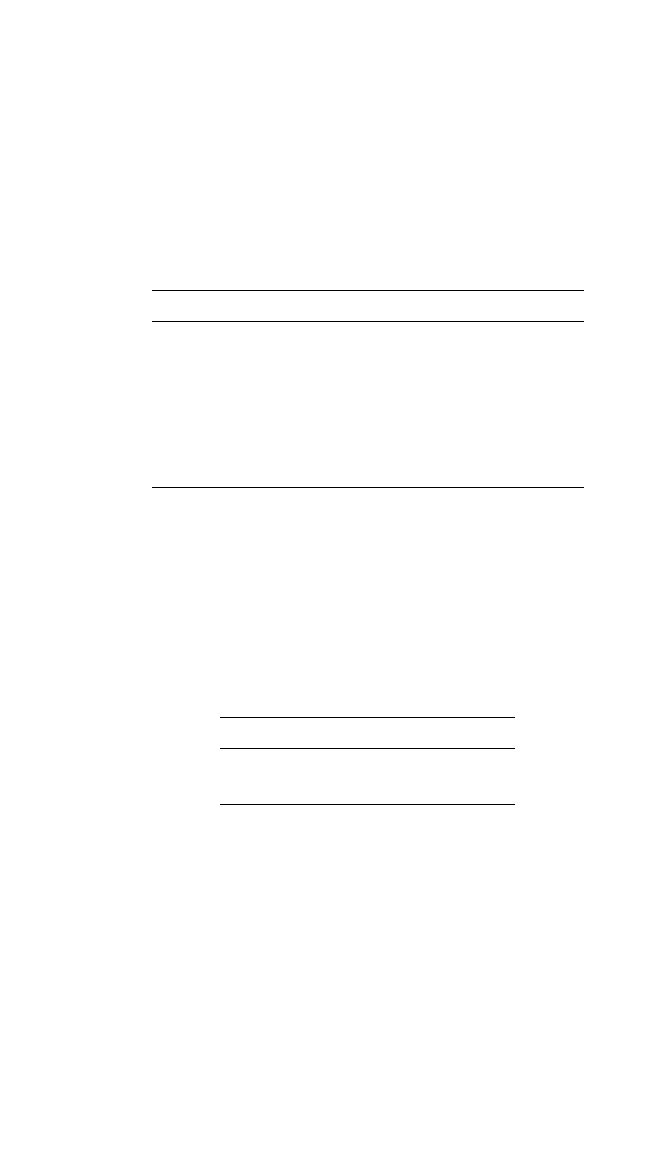
the following family arrangements: a step-parent family, a family consisting

of one parent and cohabiting partner, and a two cohabiting parents family.

11.13 A Cox regression for the log-hazard of union disruption based on the 1230

couples in the NSFH used the following predictors: relationship duration in

months (DURATION), female’s age at union inception (FAGUNION),

whether either partner experienced a parental divorce (PARENTAL), whether

the household had children under 5 (CHDN5), and whether either partner was

a minority (MINORITY). Partial results are:

(a) Is the model signiﬁcant as a whole?

(b) Compute the Wald χ

for each coeﬃcient. Which coeﬃcients are

signiﬁcant?

11.14 Added to the model in Exercise 11.13 is a nonproportional eﬀect of

PARENTAL, of the form PARENTAL * TIME, producing:

(The eﬀect of PARENTAL in this model is .079.) Test whether

PARENTAL has a signiﬁcant nonproportional eﬀect. Irrespective of the

outcome of the test, show the hazard ratio for those with versus without

parental divorce experience at 1 month’s, 10 months’, 30 months’, and

50 months’ duration.

11.15 A Cox regression for the log-hazard of union disruption based on the 1230

couples in the NSFH used the following wave 1 predictors: male partner

was violent (HEHIT), female partner was violent (SHEHIT), male’s rela-

tionship happiness (HUSHAP), female’s relationship happiness (WIFHAP),

male’s relationship commitment (HCOMMIT), female’s relationship com-

mitment (WCOMMIT). Partial results are as follows:

Variable b

PARTIME .00314

⫺2 ln L 4556.388

Variable b σ

DURATION ⫺.015 .006

FAGUNION ⫺.042 .009

PARENTAL .220 .133

CHDN5 .103 .120

MINORITY .200 .129

⫺2lnL

4599.743

⫺2lnL

4556.715

EXERCISES 415

c11.qxd 8/27/2004 2:56 PM Page 415

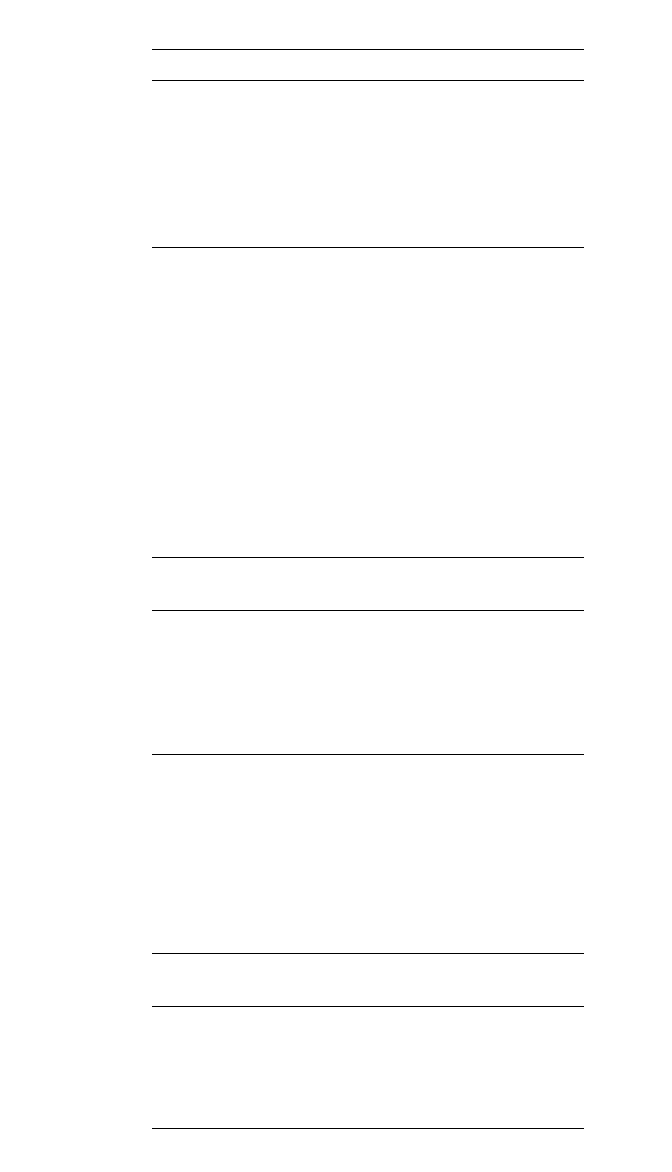
(a) Interpret the signiﬁcant (at p ⱕ .05) eﬀects.

(b) By what percent is the hazard of disruption elevated when the male has

been violent versus when the female has been violent.

SHEHIT is ⫺.05, give a 95% conﬁdence interval for the ratio of the haz-

ard of disruption for couples characterized by male violence versus cou-

ples characterized by female violence.

(d) What is the discriminatory power of the model?

11.16 The following data represent age at ﬁrst sexual intercourse or censoring for

a sample of six teenage girls, along with mother’s educational level and a

dummy for family type (1 ⫽ “two-parent biological,” 0 ⫽ “other”):

1 ⫽ uncensored; 0 ⫽ censored.

If the estimate of the eﬀect of mother’s education from a Cox model stratiﬁed

by family type is ⫺.144, give ⫺2 ln L for the stratiﬁed Cox model.

11.17 The following data represent times in months to voluntary job termination

or censoring for ﬁve employees, along with the cumulative number of days

of sick leave taken by the start of the study:

1 ⫽ uncensored; 0 ⫽ censored.

Censoring Days of

Subject Indicator

Months Sick Leave

1 1 14 2

2130

31912

4 0 15 1

5024

Censoring Family Mother’s

Subject Indicator

Age Type Education

1 1 16 1 13

2 0 19 1 15

3 1 17 1 20

4 1 15 0 12

5 1 16 0 16

6 0 14 0 17

Variable b σ

HEHIT .316 .248

SHEHIT .132 .242

HUSHAP ⫺.084 .051

WIFHAP ⫺.144 .047

HCOMMIT ⫺.095 .073

WCOMMIT ⫺.425 .070

LRχ

150.153

416 INTRODUCTION TO SURVIVAL ANALYSIS

c11.qxd 8/27/2004 2:56 PM Page 416

If the Cox estimate for the eﬀect of days of sick leave is .070, give ⫺2lnL

for the Cox model with days of sick leave as the predictor.

Use the Union Disruption Data for the following computer exercises involving Cox

regression.

11.18 Estimate a Cox model for the hazard of disruption as a function of MEDUC,

FEDUC, MINCOME, FINCOME, HE1, and WE1. Adjust for left truncation

using the method, outlined by Allison (1995), in which one of the predictors

is made into a time-varying covariate as follows. A covariate, say MEDUC,

is labeled MEDUCTD. MEDUCTD is then set to missing while SURVIVAL

is less than DURATION; otherwise, it is set equal to MEDUC. MEDUCTD

is then used in the model in place of MEDUC.

(a) Report the parameter estimates and note which ones are signiﬁcant.

(b) Interpret the eﬀects of FEDUC and MINCOME.

cation as well as the equality of eﬀects of male and female income using

individual Wald tests.

11.19 Test whether the eﬀects of MEDUC versus FEDUC and the eﬀects of MIN-

COME vs. FINCOME are equal using a global test for both equalities simul-

taneously.

11.20 Estimate the model in Exercise 11.15 stratiﬁed by MINORITY (minority sta-

tus of the couple), and test whether the parameter vector is invariant over strata.

11.21 Estimate a model of union disruption as a function of DURATION, FAGU-

NION, FIRSTUNI, ALCDRUG, DISAGMT, COMSTYLE, and the interaction

of DISAGMT with COMSTYLE. Estimate the impact of DISAGMT at 1 stan-

dard deviation above the mean level of communication style, and test whether

it is signiﬁcant at this level of COMSTYLE. (Hint: Use targeted centering.)

11.22 Perform May and Hosmer’s (1998) goodness-of-ﬁt test for model 3 in Table

11.2.

EXERCISES 417

c11.qxd 8/27/2004 2:56 PM Page 417

418

Regression with Social Data: Modeling Continuous and Limited Response Variables,

By Alfred DeMaris

CHAPTER 12

Multistate, Multiepisode, and

Interval-Censored Models

in Survival Analysis

CHAPTER OVERVIEW

In Chapter 11 we considered various ways of modeling single, nonrepeatable events,

using Cox’s semiparametric regression model as our primary analytic vehicle. Often,

however, event histories are more complex. For example, instead of duration at risk

terminating in only one possible state, there may be multiple destination states that

terminate duration at risk. I have already alluded to one such possibility: that mar-

riages may terminate in death as well as in separation or divorce. Or, rather than

being a one-time occurrence, the event of interest may be repeatable. Examples of

repeatable events are getting married, taking a job, getting a promotion, being arrested,

or getting pregnant. In these instances, each person may contribute several survival

spells or episodes to the data ﬁle. Or, events may take place in discrete rather than

continuous time. An example already given is promotion to a higher academic rank

in institutions of higher education. Even if events occur in continuous time, however,

duration at risk may only be recorded in terms of time intervals rather than exact

times. Such discrete or interval-censored data require diﬀerent modeling techniques

than those heretofore discussed.

In this chapter we expand our toolkit for survival analysis by considering the

modeling of multiple events, the modeling of repeated events, and the modeling of

data that are discrete or interval-censored. I begin with an exploration of models for

multiple events, focusing on the competing risks model. An alternative two-step

model is also considered for cases in which the competing risks model is not war-

ranted. I then move to a discussion of models for repeated events. Because repeated

c12.qxd 8/27/2004 2:57 PM Page 418

episodes for a given person are likely to be correlated, I discuss several approaches

to handling the dependence of survival times across cases. Finally, I detail the

approach taken when data are either interval-censored or truly discrete. As this situ-

ation necessitates the transformation of one’s data, I discuss the data-transformation

process ﬁrst and then consider how survival analysis is accomplished with the trans-

formed data ﬁle. Data for illustrating the techniques are, again, drawn from the

author’s own research.

MULTISTATE MODELS

Survival models in which duration-at-risk can terminate in any of several possible

destination states are termed multistate models (Blossfeld et al., 1989). In many

instances, event histories are characterized by multiple event types rather than a sin-

gle type. For example, duration in unmarried cohabitation can terminate in either

separation or marriage. Duration in a given job can end in either voluntary job ter-

mination, involuntary job termination, a transition to a job with a diﬀerent ﬁrm, or a

promotion (or demotion) within the same ﬁrm. Duration in college can end in drop-

ping out of school, a transfer to a diﬀerent college, or graduation. The most common

approach to analyzing these types of event histories is the competing risks model.

The model is predicated on two key assumptions. First, it is assumed that the transi-

tion to each event type is governed by a separate causal process. An alternative

model that assumes the same underlying process for all transitions is discussed

below. Second, it is assumed that conditional on model covariates, the multiple event

types are independent of each other. That is, the hazard of any given event type is

unrelated to the hazard of any other event type. With respect to duration in college,

for example, this would mean that those who are at especially high risk of transfer-

ring to another school are not, as a result, at any higher or lower risk for dropping

out than others. A model that allows for dependence among events is also discussed

below.

Modeling Type-Speciﬁc Hazard Rates

Suppose that for each person, i, there are a total of m ⫽ 1,2,...,Q diﬀerent possi-

ble destination states that could terminate his or her duration at risk. Further, let T

represent the variable containing the survival time for the ith person and let M

rep-

resent the variable denoting the event type that the ith person transitioned to at time

⫽ t. Competing risks models utilize type-speciﬁc hazard rates of the form

(t) ⫽ lim

∆t→0

. (12.1)

The probability in the numerator of equation (12.1) is identical, apart from the i sub-

script, to that in equation (11.1.) deﬁning the hazard for single events, except for the

addition of “M

⫽ m.” This probability is now interpreted as the conditional proba-

bility of event occurrence in some small interval of time, given survival up to the

P(t ⱕ T

⬍ t ⫹ ∆t, M

⫽ m 冟 T

ⱖ t)

ᎏ

ᎏᎏᎏᎏ

∆t

MULTISTATE MODELS 419

c12.qxd 8/27/2004 2:57 PM Page 419

beginning of that interval and given that the event is of the mth type. In words, h

(t)

is the instantaneous rate of occurrence of the mth event type to the ith person at time

t given survival up to that time. One way of thinking about these hazards is to deﬁne

as the time at which the mth event type occurred to the ith case and to imagine that

each case has a set of T

, T

,...,T

times attached to it. However, in that the

occurrence of one event removes one from the risk of occurrence of any other

events—and hence the name competing risks—we only observe one time, T

, the one

that is the smallest (Allison, 1995). As before, of course, observations who are still

at risk at the end of the study or who are lost to follow-up are considered censored.

The overall hazard of event occurrence at any given time is simply the sum of haz-

ards for all possible event types. That is,

(t) ⫽

冱

m⫽1

(t).

A Cox model for competing risks takes the form

(t) ⫽ h

(t) exp(x

⬘

ββ

). (12.2)

Noteworthy is the fact that the baseline hazard function and the coeﬃcient vector are

both subscripted with “m.” This implies that separate processes are allowed to char-

acterize each type-speciﬁc hazard: Each can have a diﬀerent baseline hazard func-

tion and a diﬀerent set of eﬀect parameters. [More generally, each hazard can even

include diﬀerent explanatory variables or be modeled using a diﬀerent parameteri-

zation of survival time; see Allison (1995).] It turns out that the partial likelihood

function for model (12.2) factors into distinct partial likelihoods for each event type

if the competing events are considered censored cases (Allison, 1995). What this

means is that the parameters of equation (12.2) can be estimated by estimating a Cox

model for each separate event type while treating the competing events and censored

cases all as censored observations. Hence, estimating a competing risks model

involves no new techniques over those that were covered in Chapter 11. The analy-

sis of each diﬀerent transition produces a LRχ

test and a set of estimates that are

asymptotically normally distributed, enabling the usual Wald tests and conﬁdence

intervals pertaining to the given event type.

One new question arises, however. We might ask whether a separate model is

really necessary for each event type, instead of simply treating all events the same

and estimating equation (11.11), the Cox model for a single event. A test statistic for

the null hypothesis that the same process determines all transitions is formed as fol-

lows. First, estimate equation (12.2) in the manner described above. Then sum all M

of the minus twice log-likelihoods for the resulting Cox models as

⫺2lnL

⫽

冱

m⫽1

⫺

2lnL

Then code as the same “event” all M of the diﬀerent event types and estimate a Cox

model for the occurrence of an “event.” Denote ⫺2 ln L for this model as ⫺2lnL

Assume there are K predictors in the model, in general. The test statistic for testing

420 MULTISTATE, MULTIEPISODE, AND INTERVAL-CENSORED MODELS

c12.qxd 8/27/2004 2:57 PM Page 420

model invariance to event type is

∆χ

[K(M⫺1)]

⫽⫺2lnL

⫺ (⫺2lnL

), (12.3)

which under the null hypothesis of invariance is distributed as chi-squared with

K(M ⫺ 1) degrees of freedom. The term K(M ⫺ 1) represents the diﬀerence in the

number of parameters estimated to construct L

versus L

. A signiﬁcant result sup-

ports the competing risks approach.

Example: Transitions Out of Cohabitation

In a recent article the author examined survival time in the state of unmarried cohab-

itation for 411 cohabiting couples in the NSFH (DeMaris, 2001). Couples were all

cohabiting in wave 1 of the survey, at which time several characteristics of the cou-

ples were measured. In wave 2 of the survey interviewers recorded whether the cou-

ple was still together or not. If the couple had separated, the date of separation was

recorded. If the couple had married, the date of marriage was recorded. Thus, two

transitions were possible: separation and marriage. In all, 85 couples were still cohab-

iting unmarried, while 173 had married and 153 had separated. Those who were still

cohabiting unmarried were considered censored observations.

Demographic predictors of the hazard of a transition included female’s age at

union inception, relationship duration (in months) as of the wave 1 survey, whether

either partner was a minority, and whether the couple experienced a birth to the

union between waves 1 and 2, the last being a time-varying covariate. Several other

measures tapped the quality of the relationship as measured in wave 1: frequency of

open disagreement, conﬂict resolution style, each partner’s relationship happiness

(on a scale from 1 ⫽ “very unhappy” to 7 ⫽ “very happy”), and each partner’s per-

ception of relationship stability (on a scale from 1 ⫽ “very high probability of sepa-

rating” to 5 ⫽ “very low probability of separating”). The focus variables pertained to

intimate violence experienced by the couple. Measures of intimate violence con-

sisted of dummies for whether or not the male or the female had been violent with

each other in the past year and whether or not the relationship had been character-

ized by intense male violence. The latter was coded 1 if the male had been the only

violent partner, or both were violent but the male’s violence was more frequent, or

the female was the only injured partner. The primary hypothesis was that violence

by either partner, and especially intense male violence, would elevate the risk of sep-

aration and diminish the risk of marriage, net of other regressors.

I estimated a competing risks model by ﬁrst specifying a Cox model for the haz-

ard of separation, treating both continuous cohabitation and marriage as censored

cases. Then I speciﬁed a Cox model for the hazard of marriage, treating continuous

cohabitation and separation as censored cases. As couples had been cohabiting for

anywhere from less than one month to over 18 years when interviewed in wave 1,

both models were adjusted for left truncation. The results are shown in Table 12.1.

At ﬁrst glance, it appears that the transition to marriage is better accounted for

than the transition to separation. The discriminatory power, using

, of models for

MULTISTATE MODELS 421

c12.qxd 8/27/2004 2:57 PM Page 421

separation and marriage are .118 and .189, respectively. Only four eﬀects are signiﬁcant

for the risk of separation. Predictably, couples with a more positive conﬂict resolu-

tion style have lower hazards of separation than others. Also, consistent with the ear-

lier study of union disruption reported in Chapter 11, couples who were older at

union inception, as tapped by the female’s age at union inception, have lower risks

of separating. Although neither partner’s violence per se has an eﬀect on separation,

couples characterized by intense male violence have hazards of separation that are

higher than others’ by a factor of exp(.731) ⫽ 2.077; or their hazards of separating

are about twice as high as others’. A birth to the union between survey waves reduces

the hazard of separation, similar to its eﬀect found in Chapter 11 for the sample that

included marrieds.

Several eﬀects are signiﬁcant when predicting the transition to marriage. A more

positive conﬂict resolution style hastens the transition to marriage, as does a greater

frequency of disagreement. The latter eﬀect may well be due to dissatisfaction with

being unmarried and conﬂicts over whether or when to make the transition to mar-

riage. Surprisingly, the only eﬀect of factors measuring violence is for violence by

the female partner, which lowers the transition rate to marriage. I have earlier spec-

ulated that as it is still customary for the male to propose marriage, her violence may

inhibit that step on his part (DeMaris, 2001). Minority couples have lower hazards

422 MULTISTATE, MULTIEPISODE, AND INTERVAL-CENSORED MODELS

Table 12.1 Competing Risks Models for Exits from Unmarried

Cohabitation

Transition to Transition to

Predictor Separation

Marriage

Open disagreement ⫺.013 .073**

Conﬂict resolution style ⫺.155* .138*

Male’s violence ⫺.620 .755

Female’s violence .479 ⫺1.286*

Intense male violence .731* ⫺.307

Union birth

⫺.878* ⫺2.367**

Female’s age at union ⫺.035** ⫺.013

Relationship duration (months) ⫺.006 ⫺.010

Minority couple ⫺.062 ⫺.765***

Male’s relationship happiness .009 .196*

Female’s relationship happiness ⫺.153 ⫺.179*

Male’s relationship stability ⫺.212 .321**

Female’s relationship stability ⫺.027 .312*

Likelihood ratio χ

51.896*** 86.126***

Degrees of freedom 13 13

Note: n ⫽ 411.

Survival time is censored upon transition to marriage.

Survival time is censored upon transition to separation.

Time-varying covariate.

* p ⬍ .05. ** p ⬍ .01. *** p ⬍ .001.

c12.qxd 8/27/2004 2:57 PM Page 422

of marriage, net of other factors. Somewhat counterintuitively, experiencing a birth

to the union inhibits the transition to marriage. However, this eﬀect is consistent with

others’ ﬁndings. In particular, Wu and Balakrishnan (1995) suggest that those who

are comfortable with having children outside of marriage are probably more ideo-

logically committed to long-term cohabitation as an alternative to marriage. The

remaining indices of marital quality have predictable eﬀects except for the female’s

relationship happiness: The happier she is with the relationship, the lower the haz-

ard of marriage. Most likely this just reﬂects the fact that if women are happy with

the relationship as is, they are reluctant to formalize the union.

Test for Model Invariance. Although regressor eﬀects appear to be quite diﬀerent for

the event of separation, as opposed to marriage, this could simply be the result of

sampling error. As mentioned, the null hypothesis of model invariance is that the

same baseline hazard function and the same parameter vector characterize each

transition type. This hypothesis was evaluated by estimating a Cox model for any

transition out of cohabitation, where marriage and separation are treated as the same

event, and employing the test statistic in equation (12.3). Minus twice the log likeli-

hood for the combined-event model was 2907.772, while ⫺2 lnL for the models for

separation and marriage, respectively, were 1314.038 and 1512.889. The test statistic is,

therefore, ∆χ

⫽ 2907.772 ⫺ (1314.038 ⫹ 1512.889) ⫽ 80.845. As the model has 13

covariates, the degrees of freedom equal 13(2 ⫺ 1) ⫽ 13. At a p-value of less than

.00001, the test is quite signiﬁcant, suggesting that the two events are characterized

by diﬀerent hazard processes.

Alternative Modeling Strategies

Two-Step Approach. As indicated, the competing risks model presumes that transi-

tions to diﬀerent end states are characterized by diﬀerent causal processes acting in

parallel (Allison, 1995). However, some multistate processes may follow a diﬀerent

pattern. For example, the transition to a romantic union from the single state may be

determined primarily by one set of factors, such as subjects’ opportunities to meet

potential partners or their own attractiveness in the marriage market. However,

whether that union is an unmarried cohabitation rather than a marriage may be more

strongly determined by other factors, such as subjects’ educational level, religiosity,

or family background. This raises the possibility of an alternative modeling strategy

in which one mechanism is allowed to govern the timing of a transition, in general,

and a separate mechanism governs the type of transition, given that a transition

occurs. Dubbed the two-step approach by Hachen (1988), the model is estimated by

ﬁrst estimating a survival model—say, the Cox model—for the transition to any

state. In this case, all outcome states are treated the same (i.e., they are all coded as

the same state). In a second step, only the subjects who made a transition are

selected, and a multinomial (or binary) logit model is estimated to examine the

impact of model covariates on which state is selected. In this second analysis, the log

of survival time is included as a covariate (Allison, 1995). Note that this second step

is not an event history analysis.

MULTISTATE MODELS 423

c12.qxd 8/27/2004 2:57 PM Page 423

The choice of whether to employ the competing risks or two-step approach is

strictly a theoretical decision. Allison (1995) suggests that the two-step approach is

especially appropriate if the diﬀerent destination states are alternative means for

achieving the same goal, as in married versus unmarried cohabitation. By this crite-

rion, the competing-risks model is clearly more appropriate for the analysis of cohab-

iting transitions, as separation and marriage fulﬁll very diﬀerent goals for cohabitors.

Hachen (1988) provides detailed guidelines concerning which model to use, but these

are more conceptually complex. Let P(m) represent the conditional probability that

the mth state is entered, given transition to some state. Hachen suggests that the two-

step model is to be preferred whenever the eﬀect of covariates on a transition, in gen-

eral, is invariant to changes in the P(m) for m ⫽ 1,2,...,Q. One example given by

Hachen considers the eﬀect of taking a high school sex-education class on the ﬁrst

type of contraception used during sexual intercourse. Suppose for some reason the

availability of, say, IUDs to adolescents were suddenly curtailed. If the eﬀect of high

school education on the hazard of ﬁrst contraceptive use in general is not aﬀected by

the lowered probability of IUD use, the two-step model should be employed.

Otherwise, the competing risks model would be preferable.

Dependence of Events. The assumption of competing risks models that alternative

destination states are independent of each other may often be untenable. Instead,

unmeasured factors may link each of the states. Using, again, the formation of the

ﬁrst romantic union as an example, it is likely that unmeasured characteristics of

individuals, such as a need for intimate companionship, raise or lower the risk of

union formation, in general. Therefore, the hazard of cohabitation and the hazard of

marriage would tend to be correlated across cases. Hill et al. (1993, p. 247) maintain

that hazard models that ignore this type of dependence among hazards “may provide

inaccurate estimates of base hazard rates or parameters.” The authors have formu-

lated a shared unmeasured risk factors (SURF) model to adjust for correlated haz-

ards, which can be estimated using conventional software. The technique currently

has several limitations, however. It has only been formulated for the case of two

competing risks. Moreover, only a positive correlation between risks is allowed for;

and the approach assumes that the two-step model is appropriate. If these conditions

are satisfactory, the model can be estimated via a two-stage procedure that is detailed

in the authors’ article (Hill et al., 1993).

MULTIEPISODE MODELS

Models for repeated events are termed multiepisode (Blossfeld et al., 1989) or recur-

rent event models (Hosmer and Lemeshow, 1999). Rather than contributing just one

spell to the data ﬁle, each case now contributes e ⫽ 1,2,...,E potential spells to the

ﬁle, where e represents a given event number, and E the total number of events expe-

rienced by the ith case. Each spell is a survival time in the nonevent state until the

event recurs. There are several potential ways of modeling repeated events (see, e.g.,

Hosmer and Lemeshow, 1999). The model discussed here is that advocated by

424 MULTISTATE, MULTIEPISODE, AND INTERVAL-CENSORED MODELS

c12.qxd 8/27/2004 2:57 PM Page 424