Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables

Подождите немного. Документ загружается.

MODELING INTERVAL-CENSORED DATA 435

Table 12.3 Union Disruption Data in Couple versus Couple-Period Formats

A. Couple Data

FD D D

AU UC U

GR D U ROCR

UA UAN THOT

N T R PI O OHO

II MABBNMM

IOO ORI I LAA

DN N S TR R Y R R

18 28.75 9 33 1 0 1 0

630 23.92 3 38 1 0 0 1 13

25 21.67 21 67 0 1 51 0 0

B. Couple-Period Data

FCD

AUCOI

GNOHS

UBHTR

NT I OO U

II RNMP

IOM T LA T

DN E H YR D

18 28.75 2 0 1 0 0

18 28.75 3 0 1 0 0

18 28.75 4 0 1 0 0

18 28.75 5 0 1 0 0

18 28.75 6 0 1 0 0

18 28.75 7 0 1 0 1

630 23.92 1 0 0 0 0

630 23.92 2 0 0 0 0

630 23.92 3 0 0 1 0

630 23.92 4 0 0 1 0

630 23.92 5 0 0 1 0

630 23.92 6 0 0 1 0

630 23.92 7 0 0 1 1

25 21.67 4 0 0 0 0

25 21.67 5 0 0 0 0

25 21.67 6 0 0 0 0

25 21.67 7 0 0 0 0

25 21.67 8 0 0 0 0

25 21.67 9 0 0 0 0

25 21.67 10 0 0 0 0

25 21.67 11 0 0 0 0

25 21.67 12 1 0 0 0

25 21.67 13 1 0 0 0

25 21.67 14 1 0 0 0

25 21.67 15 1 0 0 0

(Continued)

c12.qxd 8/27/2004 2:57 PM Page 435

15 time intervals representing survival time. Actually, after adjusting for left trunca-

tion, there were 20 six-month intervals of survival time. But I collapsed intervals 15

to 20 into the value 15 in order to have enough uncensored observations in each

interval. The logit model is an approximation to the Cox model shown as model 5 in

Table 11.2. However, there are two key diﬀerences. First, the Cox model includes

prior relationship duration. This is not possible with the discrete-time approach since

prior duration is already incorporated into the time-interval dummies. Second, the

discrete-time model includes the eﬀect of time on the log-hazard, which is ignored

in the Cox model.

The time dummies seem to suggest somewhat of a declining trend in the hazard,

in that with the exception of time interval 9, log-hazards are elevated in the ﬁrst three

intervals, compared to other intervals, and signiﬁcantly so, compared to the last

interval. Otherwise, covariate eﬀects in the logit model tend to mirror those in the

Cox model except for the regressors alcohol or drug problem and open disagree-

ment, which are not signiﬁcant in the logit model. The proper interpretations of logit

model eﬀects would be in terms of the odds of dissolution. However, given the small

probabilities of disruption in each time interval, as seen in Table 11.1, the eﬀects can

safely be interpreted in terms of hazard ratios. Hence, each unit improvement in

conﬂict resolution style is estimated to reduce the hazard of disruption at any given

time by a factor of exp(⫺.205) ⫽ .815, and so on. A more accurate estimate of the

“underlying” Cox model is shown as model 1 in Table 12.4. This is equation (12.17),

again estimated using time-interval dummies. Although the eﬀects are similar to

those in the logit model, the coeﬃcients for continuously cohabiting, union birth,

436 MULTISTATE, MULTIEPISODE, AND INTERVAL-CENSORED MODELS

Table 12.3 (Continued)

Variable Deﬁnitions

ID Couple identiﬁcation number

FAGUNION Female’s age at union inception

DURATION Number of months from inception of union until beginning of

observation period

DURMOS Number of months from beginning of observation period until either

disruption or censoring

APART Censoring indicator at the couple level

UNIBIR Time-invariant dummy for a union birth

DURTOBIR Number of months from beginning of observation period until a

union birth

COHONLY Dummy for continuous cohabitation

COHMAR Time-invariant dummy for cohabitations that transitioned to marriage

DURTOMAR Number of months from beginning of observation period until the

transition to marriage

TIME Number of the current time interval

UNBIRTH Time-varying dummy for occurrence of a union birth

COHTOMAR Time-varying dummy for cohabitations that transitioned to marriage

DISRUPTD Censoring indicator at the couple-period level

c12.qxd 8/27/2004 2:57 PM Page 436

and conﬂict resolution style, in particular, are closer to the Cox results. Again, expo-

nentiating the coeﬃcients in model 1 provides estimates of the hazard ratios for unit

increases in the predictors.

Parameterizing the Hazard Function. An advantage of the discrete-time approach is

that one can explore various parameterizations of the hazard as a function of time to

see which best ﬁts the data. If these functions imply nested models, we can use ∆χ

to test whether the eﬀect of time can be represented more parsimoniously than in the

model that employs the time-interval dummies. I therefore examined a series of

nested models, beginning with a model excluding the eﬀect of time altogether. That

is, I began by simply omitting the time-interval dummies from the model and tested

whether a signiﬁcant loss in ﬁt resulted. If no loss in ﬁt were experienced,

MODELING INTERVAL-CENSORED DATA 437

Table 12.4 Discrete-Time Approximations to Continuous-Time Models of Union

Disruption

Logit

Complementary Log-Log Models

Predictor Model Model 1 Model 2

Intercept ⫺1.344* ⫺1.517** ⫺1.132*

Time interval 1 1.373*** 1.335***

Time interval 2 .951** .948**

Time interval 3 .658* .649*

Time interval 4 .455 .416

Time interval 5 .108 .129

Time interval 6 .362 .359

Time interval 7 .338 .337

Time interval 8 .496 .487

Time interval 9 .661* .644*

Time interval 10 ⫺.043 ⫺.046

Time interval 11 .324 .322

Time interval 12 .204 .199

Time interval 13 .528 .523

Time interval 14 .533 .518

Time interval number ⫺.037*

Female’s age at union ⫺.056*** ⫺.054*** ⫺.054***

Both in a ﬁrst union ⫺.628*** ⫺.609*** ⫺.612***

Alcohol or drug problem .284 .287 .275

Continuously cohabiting 1.643*** 1.573*** 1.587***

Cohabiting to married

.355 .349 .351

Union birth

⫺.568*** ⫺.555*** ⫺.547***

Open disagreement .027 .027 .025

Conﬂict resolution style ⫺.205*** ⫺.190*** ⫺.188***

Note: n ⫽ 1230; number of couple periods is 12,480.

Time-varying covariate.

* p ⬍ .05. ** p ⬍ .01. *** p ⬍ .001.

c12.qxd 8/27/2004 2:57 PM Page 437

a constant-hazard model would be indicated. However, ∆χ

for the constant-hazard

model (results not shown), compared to model 1, was 26.826, which, with 14 df was

signiﬁcant at p ⫽ .02. I next ﬁtted a series of polynomial models in time (a variable

whose values represent time intervals) beginning with a linear term for time, then

adding a quadratic term, a cubic term, and a quartic term, and compared all to model

1. The linear model had ∆χ

⫽ 20.801, which, with 13 df, was not quite signiﬁcant

(p ⫽ .077). Adding a quadratic term did not improve ﬁt, although quadratic, cubic,

and quartic models also resulted in no signiﬁcant loss in ﬁt, compared to model 1.

Due to its greater parsimony, however, I present the linear model (model 2) in Table

12.4. Again, results are approximately the same as for the other two models in the

table. The signiﬁcant and negative eﬀect of time interval number in model 2 indi-

cates, as previously suggested, that the hazard of disruption is declining with time.

However, recall that unmeasured heterogeneity could also be responsible for such a

trend. A discrete-time model that adjusts for unmeasured heterogeneity has been dis-

cussed by Land et al., (2001).

Advantages of the Discrete-Time Approach. The discrete-time approach has some

clear advantages over the Cox model and over parametric models such as the expo-

nential or Weibull. Therefore, even with continuous-time data, it may at times be

advantageous to convert one’s data to a discrete-time format in order to beneﬁt from

these features. First, there is the issue of tied survival times. For example, for the

unemployment data considered in Chapter 11 (as well as below), fully 33.9% of

spells were tied at a survival time of one month. About 15% were tied at two months,

10.2% at one-half a month, and 9.2% at three months. When there are many tied sur-

vival times in the data, the Cox model becomes unreliable (Yamaguchi, 1991). On

the other hand, ties pose no problem for the discrete-time approach. Second, esti-

mation of the Cox model becomes quite time-consuming when there are many time-

varying covariates in the model. With the discrete-time approach, the number of such

covariates is immaterial, as they are simply incorporated directly into the data set.

Third, software for Cox models typically renders the creation of time-varying covari-

ates transparent to the analyst. One just has to trust that they are being created cor-

rectly. In the discrete-time method, one can visually inspect the records to ensure

correct coding. Fourth, the discrete-time approach allows one to explore the shape of

the hazard function and to test various parameterizations of time against the unspeciﬁed

function of time implied by time-interval dummies. Finally, as with the parametric

models mentioned in Chapter 11, the discrete-time method allows for estimation of

the hazard function as well as the survival function.

Estimation of hazard and survival functions employing, say, model 2 in Table

12.4 is straightforward. The estimate of the hazard at time t is recovered from the

equation

⫽ 1⫺exp[⫺exp(β

⫹ β

t ⫹ x

⬘g)],

where x

⬘g is the linear combination of covariates and parameter estimates, apart from

the intercept and the linear eﬀect of time. The survival function, denoted S

⫽ P(T

⬎ t

438 MULTISTATE, MULTIEPISODE, AND INTERVAL-CENSORED MODELS

c12.qxd 8/27/2004 2:57 PM Page 438

is estimated using a recursion formula that is initialized at the value 1:

⫽ 1(1 ⫺ P

)(1 ⫺ P

)

...

(1 ⫺ P

[See Singer and Willett (1993) for programming suggestions for estimating P

and

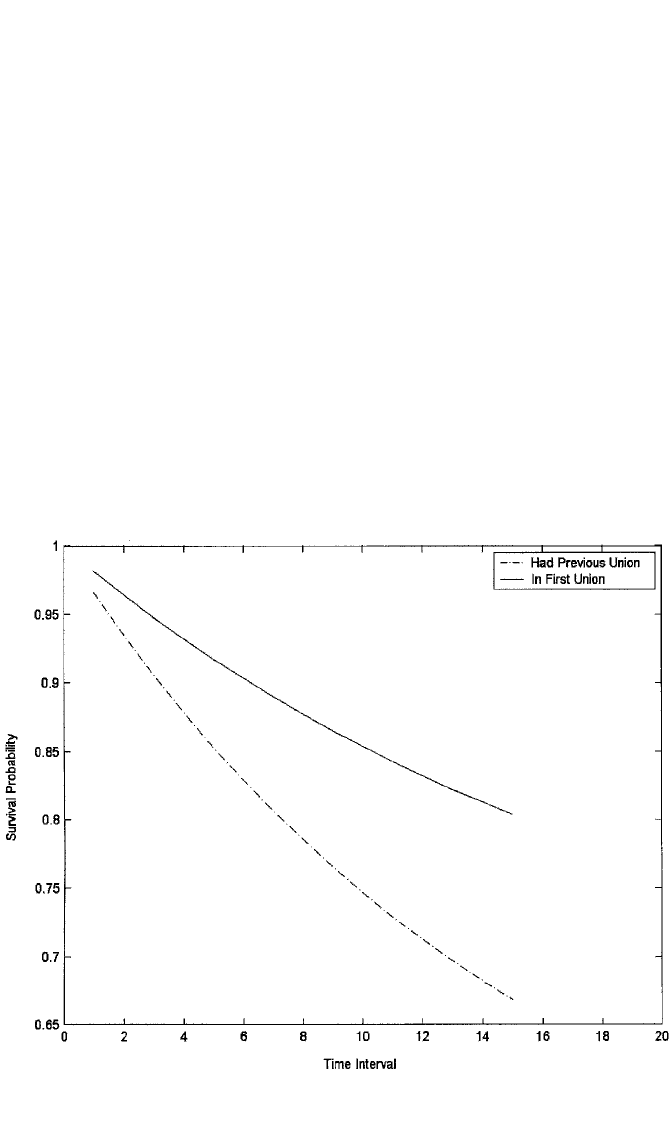
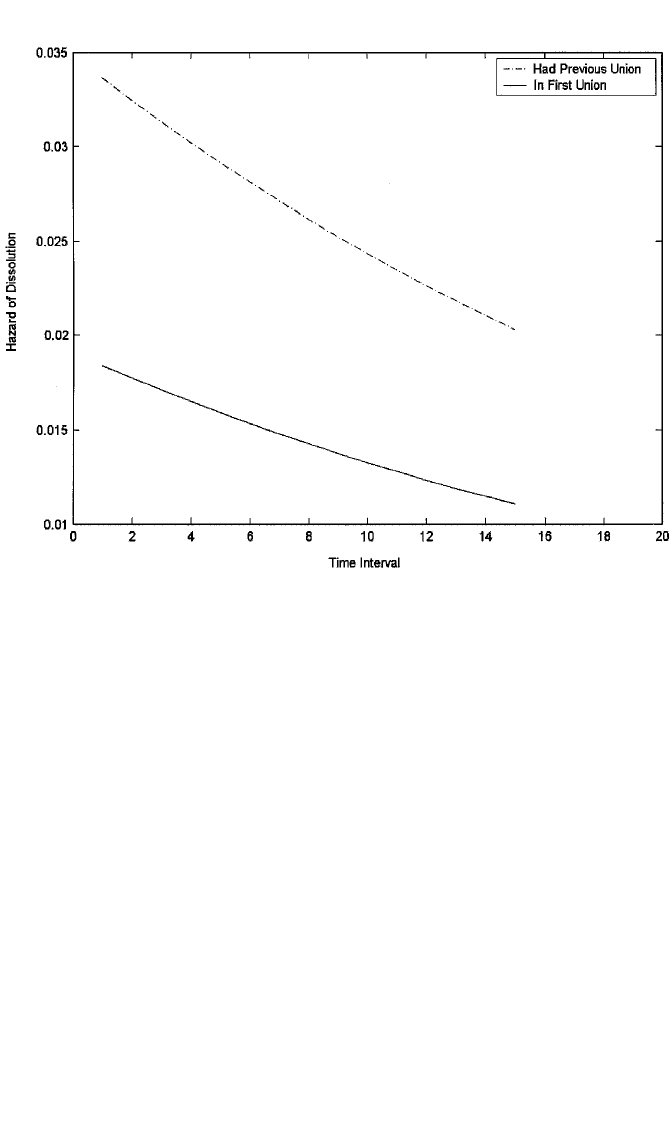
using SAS.] Figures 12.1 and 12.2 display the survival and hazard functions at

mean values of model covariates for those in ﬁrst unions as opposed to others, based

on model 2 in Table 12.4.

Cohabiting Transitions. The technique for estimating competing-risks models

when time is discrete or interval-censored parallels the method just articulated for

the single-event case. However, the likelihood function no longer factors into sepa-

rate components for each event type, as it does in continuous time (Allison, 1982).

Instead, parameter estimates are obtained by maximizing the joint likelihood involv-

ing all event types simultaneously. This is accomplished readily with multinomial

logistic regression applied to person-period data. For example, in applying the dis-

crete-time approach to the 411 cohabiting transitions analyzed above using the Cox

model, I created couple-period data in a manner similar to that described above for

MODELING INTERVAL-CENSORED DATA 439

Figure 12.1 Survival curves for event of union disruption by whether in a ﬁrst union, based on model

2, Table 12.4.

c12.qxd 8/27/2004 2:57 PM Page 439

the union disruption data. Once again, I created 15 six-month time intervals and

replicated couples’ records up to a maximum of 15 times, resulting in a total of 2265

couple-periods. Due to the longer time these couples had been together prior to wave

1, however, adjusting for left truncation resulted in values for TIME as high as 44,

equivalent to 264 months. Nevertheless, in estimating the model, I collapsed the time

variable down to ﬁve categories in order to have ample cell sizes for each type of

transition. The event indicator, called COMPRISK, was coded according to SAS’s

convention for multinomial logistic regression (in PROC CATMOD) in which the

highest code is the reference group. In this case, the reference group consisted of the

censored cases—the continuous cohabitors—and was coded 3 in all periods. For

uncensored cases, the event indicator was coded 3 until the last interval, at which

point it was coded 1 for those who separated and 2 for those who married. The

results for the multinomial logit model are shown in Table 12.5. Substantively, the

ﬁndings are quite similar to those from the Cox model in Table 12.1, except that in

the discrete-time formulation the eﬀect of female violence on the transition to mar-

riage is no longer signiﬁcant.

Transitions Out of Unemployment. As a ﬁnal example of discrete-time analyses, I

reestimated the risk of reemployment for Brazilian immigrants, earlier examined using

440 MULTISTATE, MULTIEPISODE, AND INTERVAL-CENSORED MODELS

Figure 12.2 Hazard curves for event of union disruption by whether in a ﬁrst union, based on model 2,

Table 12.4.

c12.qxd 8/27/2004 2:57 PM Page 440

Table 12.5 Discrete-Time (Multinomial Logit) Approximations to Competing-Risks

Models for Exits from Unmarried Cohabitation

Separation vs. Continuous Marriage vs. Continuous

Predictor Cohabitation Cohabitation

Intercept .754 ⫺6.895***

Time interval 1 1.378*** 2.137***

Time interval 2 .609 1.304***

Time interval 3 .471 1.488***

Time interval 4 ⫺.039 .938*

Open disagreement ⫺.010 .077**

Conﬂict resolution style ⫺.153* .153*

Male’s violence ⫺.573 .677

Female’s violence .397 ⫺1.169

Intense male violence .766* ⫺.347

Union birth

⫺1.045** ⫺2.467***

Female’s age at union ⫺.040*** ⫺.014

Minority couple ⫺.091 ⫺.798***

Male’s relationship happiness .046 .202*

Female’s relationship happiness ⫺.168* ⫺.182*

Male’s relationship stability ⫺.226 .297*

Female’s relationship stability ⫺.037 .277*

Note: n ⫽ 411; number of couple periods is 2265.

Time-varying covariate.

* p ⬍ .05. ** p ⬍ .01. *** p ⬍ .001.

Table 12.6 Discrete-Time Approximations to Multiepisode Models for Transitions

Out of Unemployment

Complementary Log-Log Models

Logit Cox Weibull

Predictor Model Approximation Approximation

Intercept ⫺1.516*** ⫺1.513*** ⫺1.477***

Time interval 2 1.168*** .916***

Time interval 3 1.763*** 1.336***

Time interval 4 1.520*** 1.180***

Time interval 5 3.596*** 2.356***

Log of time interval 1.149***

Age at unemployment ⫺.161* ⫺.129* ⫺.124*

Duration of previous job (months) ⫺.045*** ⫺.029*** ⫺.029**

Number of relatives in North America .029* .022* .024*

Cumulative time in North America ⫺.184*** ⫺.141*** ⫺.145***

Log of monthly income last job .104*** .065*** .065***

Education .061** .048*** .048**

Female ⫺.504*** ⫺.381*** ⫺.382***

Good English proﬁciency ⫺.676** ⫺.546** ⫺.530**

Note: n ⫽ 620 job spells; number of spell-periods is 1485.

* p ⬍ .05. ** p ⬍ .01. *** p ⬍ .001.

c12.qxd 8/27/2004 2:57 PM Page 441

442 MULTISTATE, MULTIEPISODE, AND INTERVAL-CENSORED MODELS

the Cox model. In this instance, the 620 unemployment spells represent the origi-

nal “person-level” data. Months of unemployment for each spell were partitioned

into ﬁve time intervals, each spell’s covariates were replicated up to ﬁve times, and

a total of 1485 spell-periods were created. An event indicator for reemployment was

coded 0 in all spell-periods for censored cases, but changed to 1 in the last period

for those who were reemployed. Both logit and complementary log-log models

were then employed to estimate the binary indicator of reemployment. Table 12.6

shows the results and is to be compared to model 1 in Table 12.2, which employs

the Cox model. The logit and Cox approximation models both simulate the Cox

model in that time is coded as a series of dummies (omitting the ﬁrst time interval)

and is therefore left unspeciﬁed. However, an assessment of various parametric

forms for the hazard function as articulated in Chapter 11 pointed to the Weibull

distribution as being most appropriate for survival time. The Weibull model is

therefore simulated in the third column of Table 12.6, by using log of time-interval

to represent time periods, rather than the time-interval dummies. In all three mod-

els, there is the suggestion of an increasing hazard of reemployment over time. The

results of all three models, but especially of the two complementary log-log mod-

els, are quite close in spirit and in parameter values to their Cox counterpart in

Table 12.2.

EXERCISES

12.1 A competing-risks model for transitions out of the current job for a popula-

tion of employees has the following form, where X ⫽ IQ and transition types

are: 1 ⫽ “quit,” 2 ⫽ “ﬁred,” and 3 ⫽ “promoted”:

(t) ⫽ .02 exp(⫺.005X ),

(t) ⫽ .005 exp(⫺ .009X ),

(t) ⫽ .015 exp(.007X ).

Give the hazard of a job transition of any kind after three years of employ-

ment for someone with an IQ of 120.

12.2 Based on the information in Exercise 12.1, by what percent is the hazard

changed for each 10-point increase in IQ for (a) the hazard of quitting, (b)

the hazard of being ﬁred, and (c) the hazard of being promoted?

12.3 In the employment-transitions problem of Exercise 12.1, if all transitions are

treated the same and a Cox model is estimated for the hazard of any transi-

tion, the likelihood is .0011. On the other hand, a competing-risks model pro-

duces the following likelihoods for quitting, being ﬁred, and getting promoted,

respectively: .3, .25, and .655. Test whether the same model applies to each

event type.

c12.qxd 8/27/2004 2:57 PM Page 442

12.4 Axinn and Thornton (1993) examined the inﬂuence of mothers’ and chil-

dren’s attitudes toward marriage and cohabitation, in 1980, on children’s

union-formation experience between 1980 and 1985. They estimated equa-

tions for (a) the cohabitation rate, in which risk sets consisted of those not

yet cohabiting or married; (b) the marriage rate, in which risk sets consisted

of those not yet cohabiting or married; (c) the marriage rate, in which risk

sets consisted of those not yet married; and (d) the union formation rate, in

which risk sets consisted of those not yet cohabiting or married. If marriage

and cohabitation are regarded as competing risks, which two equations

would represent a competing-risks model? Why?

12.5 In the Axinn and Thornton (1993) study mentioned in Exercise 12.4, which

equations must be employed to get the appropriate likelihoods for testing

model invariance over event types in a competing-risks model of marriage

versus cohabitation?

12.6 In the study of Exercise 12.4, the following equation characterizes the inter-

action of mother’s attitude toward cohabitation (higher scores indicate more

favorable attitudes) with child’s gender:lnh

(t) ⫽ ln h

(t) ⫹ x⬘g ⫹ 1.00

mother’s attitude ⫹ .51 female ⫹ 1.17 mother’s attitude * female, where x⬘g

represents the linear combination of control variables and parameter esti-

mates. Interpret this interaction eﬀect.

12.7 In the study of the hazard of reemployment of Brazilian immigrants discussed

in this chapter, suppose that we have a male immigrant with the following his-

tory: ﬁrst laid oﬀ from work in September 1985. Rehired in December 1985.

Quit his job in June 1987. Got another job in April 1988. Promoted in October

1988. Fired in October 1990. Got a new job in December 1990. Quit that job

in May 1990. Still unemployed when interviewed in October 1991. Translate

this job history into a set of unemployment spells. Show duration unemployed

in months and censoring status for each spell.

12.8 Suppose that a discrete-time approach is taken for the analysis of the hazard

of reemployment, in which survival is recorded in three-month intervals.

How many spell-periods would be contributed by the immigrant in Exercise

12.7, and in how many of these would the binary response variable—the

event indicator—be coded 1?

12.9 Goza and DeMaris (2003) examined several models for the hazard of reem-

ployment using the unemployment data on Brazilian immigrants discussed

in the text. In one discrete-time model employing the log of time interval

(LOGTIME), they ﬁnd a nonproportional eﬀect of CANADA (dummy for

residing in CANADA versus the U.S.) of the form ln[⫺ ln(1 ⫺ P

)] ⫽⫺

1.5974 ⫹ x⬘g ⫹ 1.7198 LOGTIME ⫹ .4064 CANADA ⫺ .6924 CANADA *

EXERCISES 443

c12.qxd 8/27/2004 2:57 PM Page 443

LOGTIME. Interpret the eﬀect of Canadian residence on the hazard of

reemployment (recalling that the coeﬃcients can be interpreted as eﬀects on

the log-hazard in the complementary log-log model). At what value of TIME

is the coeﬃcient for Canadian residence approximately zero?

12.10 Using the “Cox approximation” model in Table 12.6, give the estimated haz-

ards and survival probabilities for the ﬁrst two time intervals for a male

immigrant who was 40 years old at the beginning of unemployment, who

had been in his previous job for six months, who had three relatives in North

America (NA), who had been in NA for ﬁve years, who was making

$25,000.00 per year in his last job, who had a high school education, and

whose English proﬁciency was “good.”

12.11 Using model 2 in Table 12.4, give the estimated hazards and survival prob-

abilities for the ﬁrst two time intervals for a continuously cohabiting couple

in which the female was 19 at inception of the union, both partners are in a

ﬁrst union, neither partner has problems with substance abuse, there was no

union birth, the open disagreement score is 5.5, and the conﬂict resolution

style score is 2.5.

12.12 Long et al. (1993) used a discrete-time model to examine the process of pro-

motion in rank for 556 male and 450 female professors in the ﬁeld of bio-

chemistry. All people had held positions as assistant professors in research

universities at some point in their careers. Letting

αα

⬘t represent a particular

parameterization of time, their model was expressed as

⫽ ,

where the t superscript on the covariate vector denotes the potential presence

of time-varying covariates. What type of model is this? (Hint: Rewrite the

equation in a more easily recognizable form.)

12.13 In the Long et al. (1993) study, time was parameterized as a fourth-order

polynomial in years in rank. Letting t denote years in rank, the equation for

men’s hazard of promotion to associate professor, as a function of years in

rank, and apart from covariates, was

ᎏ

1 ⫺

ᎏ

⫽⫺12.221 ⫹ 4.507t ⫺ .694t

⫹ .043t

⫺ .001t

Give the estimated hazards and the survival probabilities for the ﬁrst four

years in rank for a man whose covariate values were all equal to zero.

12.14 In the Long et al. (1993) study, the equation for the hazard of promotion to

associate professor as a function of years in rank, for women, was, apart

ᎏ

ᎏᎏᎏ

1 ⫹ exp(⫺

αα

⬘t ⫺ x

⬘

ββ

)

444 MULTISTATE, MULTIEPISODE, AND INTERVAL-CENSORED MODELS

c12.qxd 8/27/2004 2:57 PM Page 444