Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables
Подождите немного. Документ загружается.


A f(r) πr
2
(the area of a circle is a function of its radius, r).
V f(r,h) πr
2
h (the volume of a cylinder is a function of its radius, r,
and its height, h).
V f(r)
4
3
πr
3
(the volume of a sphere is a function of its radius, r).
Functions can also be implicit; that is, the rule is unspecified:
Teacher salary f(county of employment).
Job satisfaction f(salary, autonomy, responsibility, role specificity).
Linear Functions. Especially important in this book, and in statistics generally, are
linear functions. Y is a linear function of one or more x’s if it can be expressed as a
weighted sum of x-values times constants plus (possibly) other constants. For exam-
ple, equations of the form y a bx are linear functions of a single x. This is a
weighted sum of a constant, b, times x, plus another constant, a. As another exam-
ple, y a b
1
x
1
b
2
x
2
b
3
x
3
is a linear function of x
1
, x
2
, and x
3
.
The function y a bx is linear in the sense that if the set of points (x,y) is plotted
on a two-dimensional graph, they will all fall on a straight line. [Correspondingly,
when y is a linear function of several x’s, the set of points (x
1
, x
2
,...,x
k
, y) falls on
a single hyperplane.]
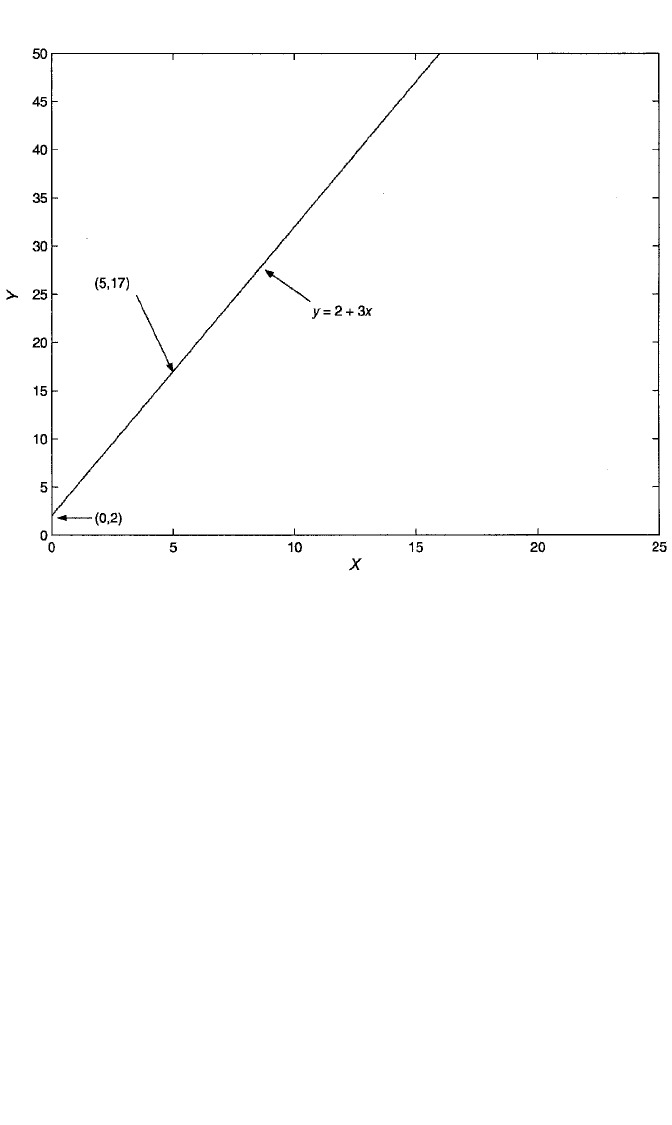
Example. Let y 2 3x. Figure A.1 presents a graph of this equation. The equation
is defined by two important components: the intercept, a (2, in this case), and the
slope, b (3, here). The intercept is the value of y when x 0. It is also the value of y
where the line of (x,y) points, implied by the equation, crosses the y-axis. The slope
of the equation indicates the number of units y changes as x increases by 1 unit. It is
also known as the ratio of the “rise” in y to the “run” in x, or slope rise/run. For
example, if x increases 5 units, from 0 to 5, y increases from 2 3(0) 2 to 2
3(5) 17. This is an increase of 15 units. The unit increase in y per unit increase in
x, however, is 15/5 3 units, which agrees with the slope value of 3 for this equa-
tion. The resulting (x,y) points achieved by plugging sample values of x into this
equation lie on the line indicated in the figure.
Point–Slope Form of a Line. If we know the slope of a linear equation and any
point on the equation, we can easily recover the equation for the line. Hence, if x
0
,y
0
is a point on the line and b is the slope, the general equation for the line is
(y y
0
) b(x x
0
). As an example, let’s find the equation for the line with slope 5.2
that passes through the point (2,9). Solution: The equation would be (y 9)
5.2(x 2) or y 9 5.2x 10.4. The resulting equation in the form y a bx is
y 1.4 5.2x. It is easily verified that the point (2,9) is on the line, since if x 2,
we have y 1.4 5.2(2) 9.
Nonlinear Function. Y can also be a nonlinear function of x. Examples are y a
MATHEMATICS TUTORIALS 455
bapp01.qxd 30.8.04 11:45 Page 455
ln x, y a e
x
or y a bx cx
2
. In each case, x enters the equation in some form
other than simply being multiplied by a constant. The graphs of such equations would
be curves rather than straight lines. In the third example here, y a bx cx
2
, notice
that y is a nonlinear function of x but it is linear in the parameters, a, b, and c. That is,
if we were to fix the value of x (say, by setting x 2) in this equation, and evaluate it
for different values of a, b, and c, it becomes a function of these parameters rather than
of x. In this event, notice that y would be a linear function of the parameters, since y is
a weighted sum of the parameter values times constants. The constants for a, b, and c,
respectively, are 1, x, and x
2
. The concept of linearity in the parameters becomes
important when we consider multiple linear regression.
Q. Exercises
(1) Find (3x 2)(y z).
(2) Find (2x 兹y
苶
z)(x
2
兹y
苶
4w).
(3) Solve
1
2
x 12 兹2
苶
4
苶
.
(4) Evaluate
2!(6
6
!
2)!
.
456 MATHEMATICS TUTORIALS
Figure A.1 Linear relationship between Y and X when Y 2 3X.
bapp01.qxd 30.8.04 11:45 Page 456

(5) Find
a
c
b
3a
cd
bπ
.
(6) Find
z
x
w
2
y
w
.
(7) Solve
兹
25
x
苶
4
9
.
(8) Find (3x
3
)(5x
2
).
(9) Find
冢
2
x
y
冣
z
.
(10) Find
(兹
兹
3
2
苶
2
苶
)
3
.
(11) Simplify ln
兹
x
2
z
苶
.
(12) Find f(x)
1
2
9x for x
1
2
,
1
3
,2.
(13) Find f(x) x
2
3x 1 for x
1
2
,
1
3
,2.
(14) Let f(x) 兹x
苶
and g(x) 2
x
. Find f(g(x)) for x 3.
(15) Let f(x) e
x
and g(x) 3 5x. Find f(g(x)) for x
1
2
.
(16) Let f(x) 2
1
2
x and g(x) 3 5x. Find f(g(x)).
(17) Find the equation for the line with slope 18 that passes through the (x,y)
point (
1
2
,
1
2
).
II. SUMMATION NOTATION AND RULES OF SUMMATION
A. Summation Notation
Anyone who has ever taken a statistics course is certainly familiar with summation
notation. It is a compact means of expressing statistical formulas involving operations
on n sample values. For example, if we have five sample values of y: y
1
, y
2
, y
3
, y
4
, and
y
5
, the sum of these five values, in summation notation, is
冱
5
i1
y
i
, which indicates the
sum y
1
y
2
y
3
y
4
y
5
. The i below the summation symbol is called the index of
summation. It indicates which elements are to be summed and ranges in integer incre-
ments from 1 to n. Since y is subscripted with i,“y
i
” indicates the y-values that are to
be summed and is known as a “variable with respect to the summation.”
B. Rules of Summation
As it is often useful to recast sums into a different form for computational (or theo-
retical) reasons, the following set of rules for working with sums will be helpful:
(1)
冱
n
i1
c nc. (The sum of a constant, n times, is n times that constant.)
(2)
冱
n
i1
cx
i
c
冱
n
i1
x
i
. (The sum of a constant times a variable with respect to the
summation is equal to the constant times the sum of the variable.)
MATHEMATICS TUTORIALS 457
bapp01.qxd 30.8.04 11:46 Page 457

(3)
冱
n
i1
(x
i
y
i
zi)
冱
n
i1
x
i
冱
n
i1
y
i
冱
n
i1
z
i
. (The sum of a sum or
difference of terms is equal to the sum or difference of the separately summed
terms.)
(4)
冱
n
i1
(x
i
y
i
)
冱
n
i1
x
i
冱
n
i1
y
i
. (It is not generally true that the sum of the prod-
uct of terms is equal to the product of the separately summed terms.)
(5)
冱
n
i1
y
x
i
i
冱
冱
n
i
n
i
1
1
x
y
i
i
. (It is not generally true that the sum of the ratio of terms is
equal to the ratio of the separately summed terms.)
C. Working with Summations
Let’s apply rules II.B(1) through II.B(3) to produce computing formulas for two well-
known statistical measures.
(1) Sample Variance. The sample variance of x is defined as s
x
2
冱
n
i1
(x
i
x
苶
)
2
/
(n 1), or, omitting the index of summation for simplicity’s sake, we have s
x
2
冱
(x x
苶
)
2
/(n 1). (We omit the index of summation when it is clear which element
is the variable with respect to summation, as it is in this case.) Now, by the rules
above,
冱
(x x
苶
)
2
冱
(x
2
2xx
苶
x
苶
2
)
(expanding the term inside the sum)
冱
x
2
冱
2xx
苶
冱
x
苶
2
[by rule II.B(3)]
冱
x
2
2x
苶
冱
x nx
苶
2
[by rules II.B(2) and II.B(1), respectively]
冱
x
2
2x
苶
nx
苶
nx
苶
2
(because x
苶
冱
x/n implies that
冱
x nx
苶
)
冱
x
2
2nx
苶
2
nx
苶
2
冱
x
2
nx
苶
2
.
Thus, a computing formula for the sample variance is
s
x
2
冱
x
n
2
1
nx
苶
2
.
458 MATHEMATICS TUTORIALS
bapp01.qxd 30.8.04 11:46 Page 458

(2) Sample Covariance. The sample covariance between x and y is defined as
cov(x,y)
冱
(x
n
x
苶
)
1
(y y
苶
)
.
Again, let’s work with the sum in the numerator:
冱
(x x
苶
)(y y
苶
)
冱
[xy xy
苶
x
苶
y ( x
苶
)(y
苶
)]
(expanding the term inside the sum)
冱
xy
冱
xy
苶
冱
x
苶
y
冱
(x
苶
)(y
苶
)
[by rule II.B(3)]
冱
xy y
苶
冱
x x
苶
冱
y n( x
苶
)(y
苶
)
[by rules II.B(2) and II.B(1)]
冱
xy n(x
苶
)(y
苶
) n( x
苶
)(y
苶
) n( x
苶
)(y
苶
)
冱
xy n(x
苶
)(y
苶
).
A computing formula for the covariance is, therefore,
cov(x,y)
冱
xy
n
n
1
(x
苶
)(y
苶
)
.
The reader will notice, in the derivations above, that both x
苶
and y
苶
are treated as con-
stants. This, in fact, is the case with respect to the summation. That is, once the n
cases have been employed to compute the means of x and y, these entities are then
constant values with respect to any further summations.
D. Weighted Sums
One sum that is particularly important in statistics is the weighted sum. A weighted
sum of a set of variables, x
1
, x
2
, ..., x
k
, takes the form
冱
w
k
x
k
, where the w
k
are the
weights and k is the index of summation. In this case, each x
k
has an associated weight,
w
k
, by which it is multiplied. This type of sum is also called a linear combination or a
linear composite of the x’s. If the weights, moreover, sum to 1, the result is some type
of mean. For example, the sample mean is a weighted sum, where each x is given the
same weight, 1/n. This is easily seen, since the sample mean can be expressed as
x
苶
冱
(1/n) x. This clearly has the form
冱
w
k
x
k
, where k i, and w
i
1/n. Weighted
means are linear combinations of means (say, from different subpopulations), where
the weights are not the same for each mean. For example, the weights might be the
MATHEMATICS TUTORIALS 459
bapp01.qxd 30.8.04 11:46 Page 459

proportion of the overall population that falls into each subpopulation. If the weights
sum to 1, the result is the mean, or “average,” of the means. Finally, a linear contrast
is a weighted sum in which the weights sum to zero. Linear contrasts are widely used
to test various hypotheses about sample means in analysis of variance (ANOVA).
E. Exercises
(1) Prove that it is always true for any set of x-values that
冱
(x x
苶
) 0.
(2) Prove that for any set of n sample values x
1
, x
2
,...,x
n
, adding a constant, c,
to each value changes the mean from x
苶
to x
苶
c but does not affect the sam-
ple variance of X. That is, prove that Mean(X c) x
苶
c and that s
2
xc
s
2
x
.
(3) Prove that if any set of X-values is standardized, by converting each X-value
to Z via the formula z (x x
苶
)/s
x
, the mean of the standardized scores is
always zero and the standard deviation of the standardized scores is always
1. That is, prove that it is always the case that z
苶
0 and s
z
1. [Hint: Write
out formulas for the mean and standard deviation using Z instead of X, then
substitute (x x
苶
)/s
x
for Z and use the summation rules to simplify the result.]
III. COVARIANCE ALGEBRA
Many theoretical derivations of importance to statistics depend on making use of
covariance algebra. Covariance algebra consists of a set of algebraic rules for finding
variances and covariances involving variables and constants. These rules make it
possible to find variances of terms, and covariances between terms, which appear at
first glance to be quite complicated.
A. Definition
Cov(x,y) E(x µ
x
)(y µ
y
). The population (or theoretical) covariance between x
and y is the expected value, or average, of the cross-product of deviation scores in x
with deviation scores in y. [The sample estimator of this quantity is given in Section
II.C(2). Notice the difference in notation between “Cov” for the population entity and
“cov” for the sample entity.] The covariance is a quantitative measure of how two
variables vary together. Positive covariances reflect situations in which large (small)
values of x are associated with large (small) values of y. Negative covariances indi-
cate that large (small) values of x are associated with small (large) values of y.
B. Basic Rules of Covariance Algebra
Let W, X, Y, and Z be variables, and let a, b, c, and d be constants, in a given set of
data. Then:
(1) Cov(X,Y ) Cov(Y,X). Covariance is symmetric with respect to the order of
the variables.
460 MATHEMATICS TUTORIALS
bapp01.qxd 30.8.04 11:46 Page 460

(2) Cov(X,c) 0. The covariance of a variable with a constant is zero. This
makes intuitive sense, since one of these “variables” isn’t varying at all.
(3) V(X) Cov(X,X). The variance of a variable is the covariance of that variable
with itself.
(4) V(cX) c
2
V(X). The variance of a constant times a variable is the square of
the constant times the variance of the variable.
(5) Cov(aX,bY) ab Cov(X,Y). The covariance of variables multiplied by con-
stants is the product of the constants times the covariance of the variables. Or,
constants can be “pulled through” covariance operations.
(6) Cov(aX bY, cW dZ) ac Cov(X,W) ad Cov(X,Z) bc Cov(Y,W) bd
Cov(Y,Z). The covariance of two linear combinations is a linear combination
of the individual covariances. This rule shows a simple technique for finding
the covariance of any two terms. Let’s find that last covariance again, to see
how this works:
Step 1. Multiply the terms on each side of the comma together using regular algebra:
(aX bY )(cW dZ) aXcW aXdZ bYcW bYdZ.
Step 2. In the resulting sum, separate the original components of each term with
commas:
aX,cW aX,dZ bY,cW bY,dZ.
Step 3. Take the sum of the covariances of the terms joined by commas:
Cov(aX,cW) Cov(aX,dZ) Cov(bY,cW) Cov(bY,dZ)
Step 4. Apply the appropriate basic rules above to reduce the result to an expression
involving the sum of constants times covariances of variables or constants times
variances of variables:
ac Cov(X,W) ad Cov(X,Z) bc Cov(Y,W) bd Cov(Y,Z).
Notice that I’ve applied rule III.B(5) to the expression in step 3 to arrive at the
result in step 4.
C. Applications
Application 1. In linear regression, we regress Y on a set of X’s: X
1
, X
2
,...,X
K
in
a particular sample. Each b
k
(i.e., each regression coefficient) has an associated sam-
pling variance. Each pair of regression coefficients, such as b
1
and b
2
, say, has a sam-
pling covariance. Sampling variances and covariances make sense only in the
context of repeated sampling. That is, the current sample is only one of an infinite
MATHEMATICS TUTORIALS 461
bapp01.qxd 30.8.04 11:46 Page 461

number of possible samples of size n that could be drawn from the population.
Hence, the current (i.e., those from your particular sample) regression coefficients
are only one set from an infinite number of sets of regression coefficients that could
be obtained by regressing Y on the X’s in each of the infinite number of samples. The
variance of b
k
, denoted V(b
k
), is then a quantitative measure of the variation in b
k
one
would encounter from performing all of these different sample regressions. The
covariance of, say, b
1
with b
2
, denoted Cov(b
1
,b
2
), is a measure of the extent to
which the values of b
1
and b
2
, from all of these regressions, would covary.
Okay, suppose that you have two coefficients in a particular sample, say b
1
and
b
2
, and you want to test whether the population analogs of these coefficients are
equal. That is, you want to test the null hypothesis H
0
: β
1
β
2
, or H
0
: β
1
β
2
0.
The test is a t test of the form
t
(nK1)
SE
b
(
1
b
1
b
2
b
2
)
,
where SE(b
1
b
2
) is the estimated standard error of b
1
b
2
, the difference in the
sample coefficients. This standard error is the estimate of the square root of
V(b
1
b
2
), the variance of b
1
b
2
. How do we find this variance?
Realize first that b
1
and b
2
are variables over repeated sampling, and their
difference is therefore also a variable, so we can use covariance algebra to find the
difference between two variables:
V(b
1
b
2
) Cov(b
1
b
2
, b
1
b
2
)
[by rule III.B(3); notice that the constant multiplier of b
2
here is “1”]
Cov(b
1
,b
1
) Cov(b
1
,b
2
) Cov(b
2
,b
1
) Cov(b
2
,b
2
)
[by rule III.B(6)]
V(b
1
) V(b
2
) 2Cov(b
1
,b
2
)
[by rules III.B(1) and III.B(3)]. The sampling variance of b
1
b
2
can therefore be
estimated by plugging sample estimates of V(b
1
), V(b
2
), and Cov(b
1
,b
2
) into this last
expression and then taking its square root. The required sample estimates can be
found in the variance–covariance matrix of parameter estimates, which is an
optional part of standard regression output.
Application 2. Continuing our linear regression example, suppose that we estimate
an interaction model with two explanatory variables, X and Z. Our sample equation
is yˆ a bX cZ dXZ, where XZ is the cross-product of the variables X and Z.
We are interested in whether the impact of X on Y is significant at a particular level
of Z, say at z. As explained in Chapter 3, the partial slope for the effect of X on Y at
a particular level of Z is a function of Z. To see this, we factor all multipliers of X
462 MATHEMATICS TUTORIALS
bapp01.qxd 30.8.04 11:46 Page 462

in the regression equation yˆ a bX cZ dXZ, and we get yˆ a
cZ (b dZ)X. Hence, the partial slope for X is the coefficient of X in this rewrit-
ten equation, or b dZ. That is, the partial slope depends on the particular value of
Z at which it is evaluated. When Z z (a particular value of Z), the partial slope is
b dz. The test statistic for the significance of this partial slope is, like any test sta-
tistic for a partial slope, the partial slope estimate divided by its estimated standard
error. This is a t-test statistic with n K 1 degrees of freedom under the null
hypothesis, where K the total number of regressors in the model (in this simple
case, K 3).
The test is
t
(nK1)
SE
b
(
b
dz
dz)
.
How do we find SE(b dz)? You guessed it—we use covariance algebra. We have to
find an estimate of V(b dz) and then take its square root. Now, remember that if Z
is fixed over repeated sampling (or if our results are conditional on the particular val-
ues of Z in our sample), z is a constant throughout this process (of repeated sampling,
that is). That is, it doesn’t change over repeated sampling; only b and d vary. Don’t
confuse the b and d in this example with the b and d in the covariance algebra rules.
In that case they were constants. Now they’re estimated regression coefficients, and
therefore variables! So
V(b dz) Cov(b dz,b dz)
[applying rule III.B(3)]
Cov(b,b) Cov(b,dz) Cov(dz,b) Cov(dz,dz)
[by rule III.B(6)]
V(b) 2z Cov(b,d) z
2
V(d)
[using rules III.B(3), III.B(4), and III.B(5)].
Again, estimates of the required variances and covariances can be obtained from
the variance–covariance matrix of parameter estimates.
Application 3. As a third example of applying covariance algebra, I prove that the
correlation between x and y is 1 in absolute value whenever y is a perfect linear func-
tion of x. First, consider the formula for the correlation coefficient: r
xy
cov(x,y)/
s
x
s
y
. That is, the correlation between x and y is the covariance of x with y, divided by
the product of their standard deviations. Since the product of the standard deviations
can also be written as the square root of the product of the variances of x and y,we
also have that r
xy
cov(x,y)/兹v
苶
(x
苶
)v
苶
(y
苶
)
苶
.
Now, suppose that y is a perfect linear function of x. That is, suppose that y
a bx. Then cov(x,y) cov(x, a bx) b cov(x,x) b v(x) [by rules III.B(2),
MATHEMATICS TUTORIALS 463
bapp01.qxd 30.8.04 11:46 Page 463

III.B(3), and III.B(5)]. Also, v(y) v(a bx) cov(a bx, a bx) b
2
v(x) [also
by rules III.B(2), III.B(3), and III.B(5)]. Hence,
r
xy
兹
co
v
苶
v
(x
苶
(
)
x
v
苶
,y
(y
苶
)
)
苶
兹v
苶
(
b
x
苶
v
)
(
b
苶
x
2
)
v
苶
(x
苶
)
苶
v(
b
x
v
)兹
(x)
b
苶
2
苶
(the variance of x is always positive, but b may not be) b/冟b冟 b/b 1 if b 0,
or b/b 1 if b 0.
D. Exercises
For variables X, Y, and ε and constants α, β, a, b, c, and d:
(1) Find the covariance of 兹5
苶
X with 兹5
苶
Y.
(2) Find the covariance of a bX with c dY.
(3) Find the covariance of
1
2
X 3Y with 2X 9Y if Cov(X,Y) 1.2, V(X) .5,
and V(Y) 2.5.
(4) Find the variance of 2X 3Y if Cov(X,Y) 1.2, V(X) .5, and V(Y) 2.5.
(5) Suppose that Y α βX ε. Find the variance of Y in terms of the variance
of X and the variance of ε if Cov(X,ε) 0.
(6) Show that the correlation between X and Y is unchanged if X is multiplied by
a positive constant, c, and Y is multiplied by a positive constant, d, where
the correlation between any two variables U and V is ρ
UV
Cov(U,V)/
兹V
苶
(U
苶
)V
苶
(V
苶
)
苶
. [Note: The implication is, of course, that the correlation
between two variables is unchanged by a rescaling of the variables (e.g., the
correlation between height in feet and weight in pounds is the same as the
correlation between height in meters and weight in grams).]
(7) Show that the covariance between two standardized variables, Z
x
and Z
y
,is
the same as their correlation. [Hint: Use the definition of correlation in prob-
lem (6) and define Z
x
(X µ
x
)/σ
x
and Z
y
(Y µ
y
)/σ
y
.]
IV. DERIVATIVES
A. Introduction
The derivative is a very important tool for the quantification of effects of explanatory
variables in regression models. (It is also central to the estimation of parameters for
these models.) In this tutorial, I define the derivative and partial derivative and give
a series of algebraic rules for finding derivatives in various situations.
The derivative is the solution to one of the fundamental problems of calculus, the
tangent problem (Anton, 1984): Given a function Y f(x) and a point P(x
0
,y
0
) on its
graph, find the equation of the tangent line, T, to the graph at P. Figure A.2 illustrates
this problem. The tangent line, T, is the line that touches f(x) only at point P. Finding
the equation of this line requires determining its slope, which I denote as b
tan
. Once
464 MATHEMATICS TUTORIALS
bapp01.qxd 30.8.04 11:46 Page 464
