Alexandrov A.S.,Theory of Superconductivity - From Weak to Strong Coupling
Подождите немного. Документ загружается.

56
Weak coupling theory
first order in q as long as q mv
c
k
F
in equation (2.133). Then the excitation
spectrum becomes
E
k
≈
k
+ k · v
s
(2.134)
and the equation for the order parameter is
= 2E
p
k
2
k
[1 −2 f (
k
− k · v
s
)]. (2.135)
The excitation energy (equation (2.133)) is negative for some directions of k
and quasi-particles appear even at zero temperature, when the superfluid velocity
exceeds v
c
. The Landau criterion tells us that superconductivity should disappear
at v
s
>v
c
. Let us see how it happens by solving the BCS equation (2.135) in two
and three dimensions. For T = 0, we have
f (
k
−k · v
s
) = θ(−
k
+ kv
s
cos ϕ)
where ϕ is the angle between v
s
and k.Ifv
s
<v
c
, there are no quasi-particles
( f
k
= 0) and
= (0). (2.136)
Here (0) is the BCS gap (equation (2.46)) in the absence of the flow. However, if
v
s
>v
c
, there is an interval of |ϕ| arccos[
k
/(k
F
v
s
)], where f (
k
−k ·v
s
) = 1
and the gap should be different from (0). Integrating over the angle, we obtain
ln
(0)
=
2
π
k
F
v
s
d
arccos(/k
F
v
s
)
√
2
−
2
. (2.137)
in two dimensions. Calculating the remaining integral, we arrive at
ln
(0)
= ln
k
F
v
s
. (2.138)
This equation has only the trivial solution = 0. Hence, the Landau criterion
cannot be compromised in two-dimensional s-wave BCS superconductors, that
is superconductivity disappears precisely at v
s
v
c
. The superflow in three-
dimensional superconductors is different [41]. In this case, integrating over the
angle yields
ln
(0)
=
k
F
v
s
d
1 − (/k
F
v
s
)
√
2
−
2
. (2.139)
There is a non-trivial solution = 0evenifv
s
>v
c
, which is found from
ln
k
F
v
s
(0)
=
1 −
k
F
v
s
2
− ln
1 +
1 −
k
F
v
s
2
. (2.140)
It disappears only at v
s
ev
c
/2, where e = 2.718. The excitation spectrum
(equation (2.133)) has no gap but the order parameter is still non-zero if v
c
<v
s
<

Andreev reflection
57
ev
c
/2. The superconductivity in this region is gapless. Normal excitations fill the
negative part of their energy spectrum in k-space resulting in two components
(normal and superfluid), as at finite temperatures. The quasi-particles do not
fully destroy the order parameter, they renormalize it while v
s
< ev
c
/2. The
two-fluid situation at T = 0 is possible due to the Fermi statistics of quasi-
particles in the BCS superconductor because the Pauli exclusion principle limits
their density. When quasi-particles are bosons (chapter 4), the kinetic energy of a
moving condensate entirely dissipates into quasi-particles as soon as v
s
v
c
.
There are other examples of the gapless superconductivity like unconven-
tional Cooper pairs (section 2.10) and ‘dirty’ superconductors with magnetic im-
purities [42].
2.13 Andreev reflection
The Bogoliubov equations are particularly instrumental in handling the interface
between normal and superconducting metals (NS interface) and between different
superconductors (SS interface). They allow us to calculate the I –V characteristics
of tunnelling structures in the same fashion as in the conventional single-particle
tunnelling problem in quantum mechanics. If there is a potential barrier due to a
dielectric layer, NS conductance can be readily calculated using the Fermi–Dirac
golden rule (section 2.4). It shows the gap structure. In the absence of the barrier,
a new phenomenon is observed, in which an incoming electron from the normal
side of the normal/superconducting contact is reflected as a hole along the same
trajectory [46]. The Andreev reflection results in an increase in the tunnelling
conductance in the voltage range |eV|
in sharp contrast to its suppression in
the case of the barrier.
A simple theory of NS tunnelling in a metallic (no-barrier) regime [47]
follows from the one-dimensional Bogoliubov equations, which can be written
in the matrix form:
Eψ(x) =
−(1/2m) d
2
/dx
2
− µ(x)(x )
(x )(1/2m) d
2
/dx
2
+ µ(x)
ψ(x).
(2.141)
The gap (x) and the chemical potential µ(x) depend on the coordinate x
perpendicular to the contact area. In the normal state (x
0,(x) = 0,
µ(x) = µ
n
), equation (2.141) is the free-particle Schr¨odinger equation (first row)
or its time-reversed version (second row). The two-component wavefunction of
the normal metal is given by
ψ
n
(x < 0) =
1
0
e
iq
+
x
+ b
1
0
e
−iq
+
x
+ a
0
1
e
−iq
−
x
(2.142)
where momenta associated with the energy E are q
±
=[2m(µ
n
± E)]
1/2
.Here
the first and second terms describe the incident and reflected electron plane waves,
respectively. The third term describes the reflected (Andreev) hole. The hole

58
Weak coupling theory
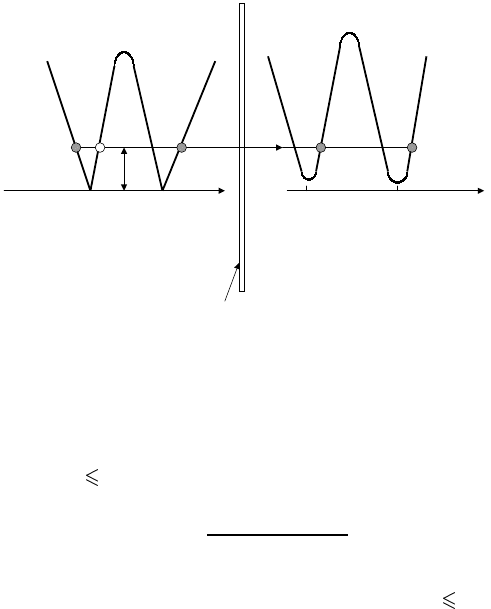
appears when the electron with the momentum q ≈ k
F
tunnels from a normal
metal into a superconducting condensate together with its ‘partner’ having the
opposite momentum −q. This simultaneous two-electron tunnelling results in the
hole excitation on the hole branch of the excitation energy spectrum near −k
F
in the normal metal (figure 2.5). In the superconductor (x 0,(x) = ,
µ(x) = µ
s
) the incoming electron can produce only outgoing particles (i.e. with
the positive group velocity ∂
k
/∂k) (figure 2.5). The solution in this region is
given by
ψ
s
(x > 0) = c
1
E + ξ
e
ik
+
x
+ d
1
E − ξ
e
−ik
−
x
(2.143)
Here the momenta associated with the energy E are k
±
=[2m(µ
s
± ξ)]
1/2
,
where ξ =
√
E
2
−
2
. The energy of the incident electron is defined in the
whole positive region (E
0), so that ξ is not necessary real.
The coefficients a, b, c, d are determined from the boundary conditions,
which are the continuity of ψ(x) and its first derivative at x = 0, as in
the conventional single-particle tunnelling problem. Applying the boundary
conditions, we obtain
1 + b = c + d (2.144)
a = c
E + ξ
+ d
E − ξ
(2.145)
q
+
(1 − b) = ck
+
− dk
−
(2.146)
and
q
−
a = ck
+
E + ξ
− dk
−
E − ξ
. (2.147)
For simplicity, we now take q
±
≈ k
±
≈ k
F
because the Fermi energy is huge
compared with the gap in the BCS superconductors. Then we find b = d = 0,
which, physically speaking, means that all reflection is the Andreev reflection and
all transmission occurs without branch crossing.
The transmission coefficient, which determines the conductance, is given by
T (E) = 1 +|a|
2
−|b|
2
. (2.148)
With b = d = 0, we obtain c = 1and
a =
E + ξ
(2.149)
from equations (2.144) and (2.145), respectively. If the incident energy (or the
voltage V = E/e) is larger than the gap (E
), ξ is real and the transmission
is obtained as
T (E) =
2E
E +
√
E
2
−
2
. (2.150)
Green’s function formulation of the BCS theory,
T = 059
(
NN
)
N
)
E
G
F
N
)
N
)
QRUPDOPHWDO
VXSHUFRQGXFWRU
LQWHUIDFH
Figure 2.5. Schematic plot of excitation energies versus k at an NS interface. The open
circle denotes the Andreev hole, the closed circles denote an incident at (1), reflected (b)
electrons, and transmitted (c), (d) quasi-particles.
It tends to one in the high energy limit (E ). Remarkably, when the energy
is below the gap (E
), the transmission is doubled compared with the normal
state limit:
T (E) = 1 +
2
(E + ξ)(E + ξ
∗
)
= 2. (2.151)
Hence, the Andreev reflection is observed as an enhancement of the tunnelling
conductance of NS metallic contacts in the gap region V
/e.The
phenomenon serves as a powerful tool in the gap determination (part 2).
2.14 Green’s function formulation of the BCS theory, T = 0
There is yet another elegant formalism introduced by Gor’kov [43], which allows
for an economic derivation of BCS results and an extension of the theory to
the intermediate coupling regime (chapter 3). Using the Heisenberg operators,
equation (2.109), let us define the time-dependent ‘normal’ G(r, r
, t) and
‘anomalous’ F
±
(r, r
, t) one-particle Green’s functions (GF) as
iG(r, r
, t) = (t)ψ
s
(r, t)ψ
†
s
(r
, 0)−(−t)ψ
†
s
(r
, 0)ψ
s
(r, t) (2.152)
iF
+
(r, r
, t) = (t)ψ
†
↓
(r, t)ψ
†
↑
(r
, 0)−(−t)ψ
†
↑
(r
, 0)ψ
†
↓
(r, t)
iF(r, r
, t) = (t)ψ
↓
(r, t)ψ
↑
(r
, 0)−(−t)ψ
↑
(r
, 0)ψ
↓
(r, t).
Here the quantum averages are calculated in the ground state of the system at zero
temperature. The operators ψ
↑
(r, t) and ψ
↓
(r
, t
) anticommute if t
= t. Hence,
F(r, r
, 0) and F
+
(r, r
, 0) are connected by the relation
F
∗
(r, r
, 0) =−F
+
(r, r
, 0). (2.153)

60
Weak coupling theory
The first time derivatives of the GFs are calculated using the equations of motion
(2.110) and (2.111). Taking into account that d(t)/dt = δ(t), we obtain a
system of two coupled equations:
i
∂G(r, r
, t)
∂t
= δ(t)δ(r − r
) +
ˆ
h(r)G(r, r
, t) + (r)F
+
(r, r
, t) (2.154)
and
i
∂ F
+
(r, r
, t)
∂t
=−
ˆ
h
∗
(r)F
+
(r, r
, t) +
∗
(r)G(r, r
, t). (2.155)
The order parameter is expressed in terms of the anomalous GF as
(r) =−2iE
p
[F
+
(r, r, +0)]
∗
. (2.156)
We can readily solve these self-consistent equations in the absence of an
external field. In a homogeneous superconductor, G(r, r
, t) = G(r − r
, t),
F
+
(r, r
, t) = F
+
(r − r
, t) and (r) is a real constant. Applying the Fourier
transforms
G(r − r
, t) =
1
2π
k
∞
−∞
dω G(k,ω)exp(ik · r − iωt) (2.157)
F
+
(r − r
, t) =
1
2π
k
∞
−∞
dω F
+
(k,ω)exp(ik · r − iωt)
we obtain
(ω − ξ
k
)G(k,ω)− F
+
(k,ω) = 1 (2.158)
(ω + ξ
k
)F
+
(k,ω)− G(k,ω) = 0.
Then the Fourier components are found to be
G(k,ω) =
ω + ξ
k
ω
2
−
2
k
=
u
2
k
ω −
k
+
v
2
k
ω +
k
(2.159)
F
+
(k,ω) =
ω
2
−
2
k
.
These expressions are well defined for any ω but not for ω =±
k
. They cannot
be used for integration with respect to ω because their simple poles are just on the
real axis of ω. We have to define a way of bypassing the poles in evaluating the
integral. The solution of the first-order differential equations (2.154) and (2.155)
are not well defined because we have not applied any initial condition so far.
The easiest way to apply the condition is to consider the normal state limit of
equation (2.159) with = 0,
G
(0)
(k,ω) =
(ξ
k
)
ω − ξ
k
+
(−ξ
k
)
ω − ξ
k
(2.160)
[F
+
(k,ω)]
(0)
= 0.

Green’s function formulation of the BCS theory,
T = 061
Integrating the Fourier transform G
(0)
(k,ω) should yield the normal state GF,
which can be directly calculated using its definition. The free-electron Heisenberg
operators are found as
ψ
s
(r, t) =
k
c
ks
exp[i(k · r − ξ
k
t)]
so that
iG
(0)
(r − r
, t) = (t)
k,k
c
ks
c
†
k
s
exp[i(k · r − k
· r
) − iξ
k
t]
− (−t)c
†
k
s
c
ks
exp[i(k · r − k
· r
) −i ξ
k
t] (2.161)
where c
†
k
s
c
ks
=δ
kk
(−ξ
k
) is the Fermi–Dirac distribution at T = 0and
c
ks
c
†
k
s
=δ
kk
(ξ
k
). Hence, we have
iG
(0)
(r − r
, t) =
k
exp[ik · (r − r
) − iξ
k
t]{(t)(ξ
k
) − (−t)(−ξ
k
)}.
(2.162)
We obtain the same result using the Fourier transform equation (2.160), if we
choose the following way of bypassing the poles:
G
(0)
(k,ω) =
(ξ
k
)
ω − ξ
k
+ iδ
+
(−ξ
k
)
ω − ξ
k
− iδ
(2.163)
where δ =+0 is an infinitesimal positive constant. Indeed let us calculate the
integral
∞
−∞
dω G
(0)
(k,ω)exp(−iωt) = (ξ
k
)
∞
−∞
dω
e
−iωt
ω − ξ
k
+ iδ
+ (−ξ
k
)
∞
−∞
dω
e
−iωt
ω − ξ
k
− iδ
. (2.164)
When t is positive the contour in both integrals of the right-hand side should
be chosen in the lower half-plane of the complex variable. The pole in the
first term is below the real axis, while the pole in the second term is found in
the upper half-plane. The first integral yields −2π i(t)(ξ
k
) and the second
integral is zero. When t is negative, the first integral is zero, while the second
one is 2πi(−t)(−ξ
k
). As a result, we recover the ideal Fermi-gas GF
(equation (2.162)). Hence, the superconducting GFs, which provide a correct
normal state limit, are
G(k,ω) =
u
2
k
ω −
k
+ iδ
+
v
2
k
ω +
k
− iδ
(2.165)
F
+
(k,ω) = u
k
v
k
1
ω +
k
− iδ
−
1
ω −
k
+ iδ
.

62
Weak coupling theory
We note that the poles of the Fourier transform of GF yields the excitation
spectrum of the superconductor.
Let us show that these GFs also provide the BCS results for the electron
distribution function and the gap. The electron density is calculated as
n
e
=−iG(r, r, −0) =−
i
2π
k
∞
−∞
dω e
−iωt
G(k,ω)
t→−0
. (2.166)
Here t is negative and the contour should be taken in the upper half-plane. Only
the second term of the normal GF, equation (2.165), contributes with the following
result:
n
e
=
k
v
2
k
(2.167)
so that the electron distribution function is v
2
k
, as it should be (see
equation (2.27)). The gap is found to be
=−2iE
p
[F
+
(r, r, +0)]
∗
=−
2iE
p
2π
k
∞
−∞
dω e
iωt
{F
+
(k,ω)}
∗
(2.168)
where t =+0. Calculating the integral with the Fourier transform
equation (2.165), we obtain the BCS equation at T = 0,
=−2E
p
k
u
k
v
k
. (2.169)
2.15 Green’s functions of the BCS superconductor at finite
temperatures
At finite temperatures, the BCS theory can be formulated with the ‘temperature’
GFs (appendix D). Following Matsubara [44], we replace time t in the definition
of the Heisenberg operators by a ‘thermodynamic time’ τ = it. Then the
temperature GF is defined as
(r, r
,τ
1
,τ
2
) =−T
τ
ψ
s
(r,τ
1
)ψ
†
s
(r
,τ
2
) (2.170)
where ψ
s
(r,τ) = exp(H τ)
s
(r) exp(−H τ)and Gor’kov’s temperature GF is
+
(r, r
,τ
1
,τ
2
) =−T
τ
ψ
†
↓
(r,τ
1
)ψ
†
↑
(r
,τ
2
).
Here the thermodynamic ‘times’, τ
1
,τ
2
, are real and positive, varying in the
interval 0 <τ
1
, τ
2
< 1/T . The double angular brackets correspond to quantum
as well as statistical averages of any operator
ˆ
A with the Gibbs distribution
(appendix B),
ˆ
A =
ν
e
(−E
ν
)/T
ν|
ˆ
A|ν≡Tr{e
(−
˜
H)/T
ˆ
A} (2.171)
Green’s functions of the BCS superconductor at finite temperatures
63
where is the thermodynamic potential and |ν are the eigenstates of
˜
H with the
eigenvalues E
ν
. The operation T
τ
performs the ‘time’ ordering according to the
following definition:
T
τ
ψ
s
(r,τ
1
)ψ
†
s
(r
,τ
2
) ≡ (τ
1
− τ
2
)ψ
s
(r,τ
1
)ψ
†
s
(r
,τ
2
)
− (τ
2
− τ
1
)ψ
†
s
(r
,τ
2
)ψ
s
(r,τ
1
). (2.172)
Actually the temperature GFs depend on the difference τ = τ
1
− τ
2
because of
the trace in their definition. Indeed let us consider τ
1
<τ
2
, so that
(r, r
,τ
1
,τ
2
) = exp(/ T ) Tr{e
−
˜
H/T
e
τ
2
˜
H
†
s
(r
)e
τ
˜
H
s
(r)e
−τ
1
˜
H
}
= exp(/T ) Tr{e
−(τ+1/T )
˜
H
†
s
(r
)e
τ
˜
H
s
(r)} (2.173)
where we have performed the cyclic permutation under the trace. Differing from
positive τ
1
and τ
2
, the variable τ is defined in the domain
−1/T
τ 1/T. (2.174)
There is a connection between GFs with negative and positive τ . Following the
definition in equation (2.170), we find, for τ>0, that
(r, r
,τ) =−exp(/T ) Tr{e
(τ −1/ T )
˜
H
s
(r)e
−τ
˜
H
†
s
(r
)}. (2.175)
Here replacing the positive τ by a negative ˜τ as τ =˜τ + 1/T , we obtain ( ˜τ<0)
(r, r
, ˜τ + 1/ T ) =−exp(/T ) Tr{e
˜τ
˜
H
s
(r)e
−( ˜τ +1/ T )
˜
H
†
s
(r
)}
=−
(r, r
, ˜τ). (2.176)
The Fourier transform theory states that if a function F(τ ) is defined over the
interval −1/T
τ 1/T , then its Fourier expansion is
F(τ ) = T
∞
n=−∞
f
n
exp(−iπ nT τ) (2.177)
where n = 0, ±1, ±2,...,and
f
n
=
1
2
1/T
−1/T
dτ F(τ ) exp(iπnTτ). (2.178)
In our case, F(τ ) =−F(τ + 1/ T ) for a negative τ and
f
n
=
1
2
(1 − e
iπn
)
1/T
0
dτ F(τ ) exp(iπnTτ). (2.179)

64
Weak coupling theory
Hence the Fourier components f
n
of the fermionic GFs are non-zero only for
odd n. As a result we can expand the temperature GFs of a homogeneous
superconductor into a Fourier series as follows:
(r, r
,τ) = T
ω
n
(k,ω
n
) exp[ik · (r − r
) − iω
n
τ ] (2.180)
+
(r, r
,τ) = T
ω
n
+
(k,ω
n
) exp[ik · (r − r
) − iω
n
τ ] (2.181)
where the discrete Matsubara frequencies are ω
n
= π T (2n + 1), n =
0, ±1, ±2,.... Differentiating the Matsubara operators with respect to τ ,we
obtain the equations of motion,
−
∂ψ
↑
(r,τ)
∂τ
=
ˆ
h(r)ψ
↑
(r,τ)+ (r)ψ
†
↓
(r,τ) (2.182)
∂ψ
†
↓
(r,τ)
∂τ
=
ˆ
h
∗
(r)ψ
†
↓
(r,τ)−
∗
(r)ψ
↑
(r,τ)
and the equations for temperature GFs,
−
∂
(r, r
,τ)
∂τ
= δ(τ)δ(r − r
) +
ˆ
h(r) (r, r
,τ)
+ (r)
+
(r, r
,τ), (2.183)
∂
+
(r, r
,τ)
∂τ
=
ˆ
h
∗
(r)
+
(r, r
,τ)−
∗
(r) (r, r
,τ). (2.184)
The order parameter is given by
∗
(r) =−2E
p
+
(r, r, 0). (2.185)
In the absence of an external field, the Fourier transforms of these equations are:
(iω
n
− ξ
k
) (k,ω
n
) −
+
(k,ω
n
) = 1 (2.186)
(iω
n
+ ξ
k
)
+
(k,ω
n
) −
∗
(k,ω
n
) = 0
and
∗
=−2E
p
T
k
ω
n
+
(k,ω
n
). (2.187)
The solution is
(k,ω
n
) =−
iω
n
+ ξ
k
ω
2
n
+
2
k
(2.188)
+
(k,ω
n
) =−
∗
ω
2
n
+
2
k

Green’s functions of the BCS superconductor at finite temperatures
65
and the equation for the order parameter takes the following form:
= 2E
p
T
k
ω
n
ω
2
n
+
2
k
. (2.189)
The sum over frequencies in equation (2.189) is calculated using the expansion of
tanh(x ) (equation (2.54)). As a result, we obtain the BCS equation for the order
parameter:
1 =
λ
2
dξ
ξ
2
+ (T )
2
tanh
ξ
2
+ (T )
2
2T
(2.190)
where the integral should be cut at |ξ|
ω
D
.
There is no direct physical meaning of poles of the Fourier transforms of
temperature GFs, which are found on the imaginary frequency axis. Nonetheless,
they allow for a direct calculation of the thermodynamic properties of the system,
for example of the gap (equation (2.190)). The kinetic properties are expressed in
terms of real-time GFs. In fact, the Matsubara GFs lead directly to real-time GFs.
A one-particle real-time GF is defined at finite temperatures as
G(k, t) =−iT
t
c
ks
(t)c
†
ks
(2.191)
with the real time t. There are also retarded G
R
and advanced G
A
GFs:
G
R
(k, t) =−i(t){c
k
(t)c
†
k
} (2.192)
G
A
(k, t) = i(−t){c
k
(t)c
†
k
}. (2.193)
Their Fourier components are analytical in the upper or lower half-plane of ω,
respectively. There is a simple connection between the Fourier components of G
and G
R,A
(appendix D):
G
R,A
(k,ω) = Re G(k,ω)± icoth
ω
2T
Im G(k,ω) (2.194)
and between those of G
R,A
and ,
G
R
(k, iω
n
) = (k,ω
n
) (2.195)
for ω
n
> 0and
(k, −ω
n
) =
∗
(k,ω
n
). (2.196)
In our case the temperature GF is
(k,ω
n
) =
u
2
k
iω
n
−
k
+
v
2
k
iω
n
+
k
(2.197)
where u
2
k
,v
2
k
= (
k
± ξ
k
)/2
k
and
k
=
ξ
2
k
+
2
. The analytical continuation
of this expression to the upper half-plane yields
G
R
(k,ω) =
u
2
k
ω −
k
+ iδ
+
v
2
k
ω +
k
+ iδ
. (2.198)
