Alexandrov A.S.,Theory of Superconductivity - From Weak to Strong Coupling
Подождите немного. Документ загружается.


36
Weak coupling theory
and (x) = 1 for positive x and zero otherwise. The wavefunction of the
open system is a superposition of different eigenfunctions of the total number
operator and the average equation (2.10) is not zero but macroscopically large
in the superconducting state. Here the double brackets mean both quantum and
statistical averages (appendix B). The substitution of equation (2.9) transforms
the BCS Hamiltonian into a quadratic form with respect to the electron operators,
˜
H =
k
[ξ
k
(c
†
k↑
c
k,↑
+c
†
−k↓
c
−k↓
) +
k
c
†
k↑
c
†
−k↓
+
∗
k
c
−k↓
c
k↑
]+
||
2
2E
p
(2.11)
where the last term is added to make sure that the ground-state energies of the
exact BCS Hamiltonian and of the approximation (2.11) are the same. Here
=−2E
p
k
(ω
D
−|ξ
k
|)c
−k
↓
c
k
↑
(2.12)
does not depend on k. Now, following Bogoliubov [4], we can replace the electron
operators by new fermion operators:
c
k↑
= u
k
α
k
+ v
k
β
†
k
(2.13)
c
−k↓
= u
k
β
k
− v
k
α
†
k
. (2.14)
This transformation reduces the whole problem of correlated electrons to an ideal
Fermi gas comprising two types of new non-interacting fermions (i.e. quasi-
particles) α and β, if we choose
u
2
k
=
1
2
1 +
ξ
k
k
(2.15)
v
2
k
=
1
2
1 −
ξ
k
k
(2.16)
and
u
k
v
k
=−
k
2
k
(2.17)
where
k
=
ξ
2
k
+|
k
|
2
. (2.18)
Then new annihilation and creation operators anticommute like fermion
operators,
{α
k
α
†
k
}={β
k
β
†
k
}=δ
kk
{α
k
α
k
}={β
k
β
k
}={α
k
β
†
k
}={α
k
β
k
}=0.
and the transformed Hamiltonian becomes diagonal,
˜
H = E
0
+
k
k
(α
†
k
α
k
+ β
†
k
β
k
) (2.19)

Ground state and excitations
37
where
E
0
= 2
k
(ξ
k
v
2
k
+
k
u
k
v
k
) +
||
2
2E
p
. (2.20)
The order parameter is determined from the self-consistent equation (2.12)
replacing the electron operators by quasi-particle ones,
= E
p
k
k
(1 − 2 f
k
) (2.21)
where
f
k
=α
†
k
α
k
= β
†
k
β
k
is the quasi-particle distribution function. Unlike the case of bare electrons the
total average number of quasi-particles is not fixed. Therefore, their chemical
potential is zero in the thermal equilibrium. They do not interact, so that
(appendix B)
f
k
=
1
exp(
k
/T ) + 1
. (2.22)
We see that there are no quasi-particles in the ground state, f
k
= 0, at
T = 0. Hence, E
0
in equation (2.19) is the ground-state energy of the BCS
superconductor. One can replace the sum in equation (2.21) by the integral using
the definition of the density of states N(E) in the Bloch band (appendix A). In
conventional metals, the Debye frequency is small (ω
D
µ) and the density of
states (DOS) is practically constant in the narrow energy region ±ω
D
around the
Fermi energy, N(E) N(E
F
). As a result, we obtain
= λ
ω
D
0
tanh
√
ξ
2
+||
2
2T
ξ
2
+||
2
dξ. (2.23)
There is a trivial solution of this equation: = 0. Above some T
c
,thisis
the only solution corresponding to the normal state. However, below T
c
there
are two solutions: = 0 and a real = 0. The system prefers to be in the
superconducting (condensed) state below T
c
because the condensation energy E
c
is negative. This energy is the ground-state energy referred to the normal state
energy. At T = 0, we have
E
c
= E
0
− 2
ξ
k
<0
ξ
k
. (2.24)
Using the definition of E
0
(equation (2.20)), we obtain
E
c
= 2N(E
F
)
ω
D
0
dξ
ξ −
ξ
2
+
2
(0)/2
ξ
2
+
2
(0)
(2.25)
38
Weak coupling theory
∆
N
N
)
(
ε
N
(
N
µ
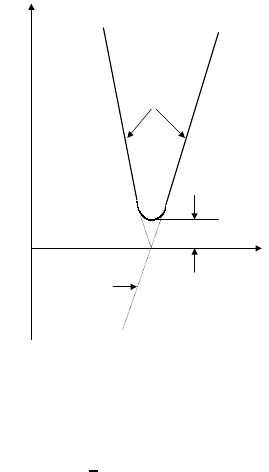
Figure 2.1. Excitation spectrum of the BCS superconductor.
where (0) is the order parameter at T = 0. Indeed, this integral is negative:
E
c
≈−
1
2
N(E
F
)
2
(0)<0. (2.26)
Far away from the Fermi surface, the quasi-particles, α and β, are electrons
with spins ‘up’ and ‘down’, respectively, if ξ
k
> 0 and holes if ξ
k
< 0. In
the vicinity of the Fermi surface, they are a mixture of both and their energy
dispersion
k
is remarkably different from that of the non-interacting electrons
and holes (see figure 2.1). The quasi-particle energy spectrum satisfies the Landau
criterion (chapter 1) of superfluidity and the critical velocity v
c
/k
F
.The
distribution of ‘bare’ electrons is of the form (T = 0)
n
k
=c
†
k↑
c
k↑
=v
2
k
(2.27)
which has a zero step (Z = 0) which differs from the Fermi distribution at T = 0
with Z = 1 (figure 2.2). This is a clear manifestation of a breakdown of the
Fermi-liquid description of attractive fermions at low temperatures. The ‘mean-
field’ approximation (equation (2.9)) replacing the pair operators
ˆ
(k) by the
anomalous averages
k
is perfectly self-consistent. Indeed, let us calculate the
commutator
[
ˆ
(k),
ˆ
†
(k)] (2.28)
to show that its expectation value is zero. Using
[c
1
c
2
, c
†
3
c
†
4
]=δ
23
c
1
c
†
4
− δ
13
c
2
c
†
4
+ δ
24
c
†
3
c
1
− δ
14
c
†
3
c
2
(2.29)
we obtain
[
ˆ
(k),
ˆ
†
(k)]=4E
2
p
(ω
D
−|ξ
k
|)
k
(ω
D
−|ξ
k
|)(1 −2c
†
k
↑
c
k
↑
). (2.30)

Ground state and excitations
39
NN
)
QRUPDOVWDWH
VXSHUFRQGXFWLQJ
VWDWH
Q
N
Figure 2.2. Distribution of electrons at T = 0.
Replacing the electron operators by the quasi-particle ones and taking the average,
we obtain
[
ˆ
(k),
ˆ
†
(k)] = 4E
2
p
(ω
D
−|ξ
k
|)
k
(ω
D
−|ξ
k
|)(u
2
k
−v
2
k
)(1 −2 f
k
) = 0
(2.31)
because the function under the integral is odd with respect to ξ
k
.
The ground state of the BCS Hamiltonian
0
is a vacuum with respect to
quasi-particles. Quasi-particles are fermions and their vacuum state is obtained
from the electron vacuum
|
0
by applying the quasi-particle annihilation operators
for every momentum k:
0
= A
k
α
k
β
k
|0. (2.32)
Indeed, every single particle state k in
0
is free from quasi-particles, so that
applying their annihilation operator to
0
, we obtain zero. The eigenfunction
should be normalized, which is the case if
A =0|
k
β
†
k
α
†
k
α
k
β
k
|0
−1/2
. (2.33)
In terms of the electron operators, we have
α
k
= u
k
c
k↑
− v
k
c
†
−k↓
β
k
= v
k
c
†
k↑
+ u
k
c
−k↓
and
0
= A
k
(u
k
v
k
− v
2
k
c
†
−k↓
c
†
k↑
)|0 (2.34)
A =
k
v
k
−1
. (2.35)
40
Weak coupling theory
Thus the ground-state wavefunction is
0
=
k
(u
k
− v
k
c
†
−k↓
c
†
k↑
)|0. (2.36)
It is a superposition of the eigenfunctions of the total number operator
ˆ
N ≡
ks
c
†
ks
c
ks
.
2.3 Meissner–Ochsenfeld effect
BCS reduced the many-body problem to a non-interacting gas of quasi-particles
allowing for an analytical description of thermodynamic and kinetic properties
of conventional superconductors. Let us first discuss the BCS theory of the
magnetic flux expulsion. We apply the perturbation theory for a linear interaction
of electrons with the vector potential A(r) taking the BCS Hamiltonian as a zero-
order one,
H
int
=−
e
m
k,q,s
(k · A
q
)c
†
k+qs
c
ks
(2.37)
where A
q
is the Fourier component of A(r). This form of the interaction
follows from the velocity operator [−i∇ − e A(r)]/m in the effective mass (m)
approximation for the band energy dispersion and the gauge, where ∇·A(r) = 0.
The field distribution in the sample is determined by the average of the current
density operator, which follows as the symmetrized form of the velocity operator
in the second quantization
ˆ
j(r) =
ˆ
j
p
(r) +
ˆ
j
d
(r) (2.38)
where
ˆ
j
p
(r) =−
e
2m
k,q,s
c
†
k+qs
c
ks
(2k + q)e
−iq·r
(2.39)
is the paramagnetic part and
ˆ
j
d
(r) =−
e
2
m
k,q,s
c
†
k+qs
c
ks
A(r)e
−iq·r
(2.40)
the diamagnetic part. The perturbed many-particle state
˜
in the first order in A
is given by
˜
=|n
α
, n
β
+
n
α
,n
β
|n
α
, n
β
n
α
, n
β
|H
int
|n
α
, n
β
E
n
α
n
β
− E
n
α
n
β
(2.41)
where |n
α
, n
β
and E
n
α
n
β
are the eigenstates and eigenvalues of the zero-
order Hamiltonian
˜
H , respectively. Applying the Bogoliubov transformation

BCS gap, critical temperature and single-electron tunnelling
41
(equations (2.13) and (2.14)) for H
int
yields the average current density at T = 0:
j
p
(r) =
2e
2
m
2
k,q
u
k+q
v
k
(2k + q)(k · A
q
)
k+q
+
k
× exp(−iq · r)(u
k+q
v
k
− u
k
v
k+q
) (2.42)
j
d
=−
ne
2
m
A(r). (2.43)
Let us assume that the magnetic field varies over the characteristic length λ
H
,
which is large compared with the coherence length ξ . In this case one can take
the limit q → 0 in equation (2.42). In this limit u
k+q
v
k
− u
k
v
k+q
= 0, while
the denominator remains finite:
k+q
+
k
> 2(0). Therefore, the paramagnetic
contribution vanishes and we obtain the London equation (chapter 1),
j(r) =−
ne
2
m
A(r). (2.44)
In the opposite limit (λ
H
<ξ), the Pippard non-local theory of the flux expulsion
follows from equations (2.42) and (2.43). In the normal state the denominator in
equation (2.42) turns out to be zero at the Fermi level and the paramagnetic current
appears to be finite. Actually, one can show that it cancels the diamagnetic part
so that the normal state current is zero in a permanent magnetic field.
2.4 BCS gap, critical temperature and single-electron
tunnelling
The BCS theory introduces the order parameter (equation (2.21)) which is also
a gap in the quasi-particle spectrum (figure 2.1) for a homogeneous system. The
value of the gap at T = 0 should be of the order of T
c
. In fact, BCS theory predicts
a universal ratio 2(0)/T
c
3.5 as follows from the master equation (2.21). At
T = 0, the non-trivial solution is determined from
1
λ
=
ω
D
0
dξ
ξ
2
+
2
(0)
. (2.45)
Integration yields
(0) 2ω
D
exp
−
1
λ
(2.46)
for λ 1, the limit to which the theory is applied. This is a remarkable
result which demonstrates the instability of the Fermi liquid for any value of the
attraction λ in agreement with the Cooper two-particle solution. The exponent in
equation (2.46) cannot be expanded in a series of λ. Thus the superconducting
ground state cannot be derived by using the perturbation theory with respect to
the pairing potential up to any order.
42
Weak coupling theory
At T = T
c
, the gap should be zero so that T
c
is determined by
1
λ
=
ω
D
0
dξ tanh(ξ/2T
c
)
ξ
. (2.47)
Integrating by parts and replacing the upper limit by infinity, we have
T
c
=
2e
C
ω
D
π
exp
−
1
λ
(2.48)
where C 0.577 is the Euler constant. The numerical coefficient in
equation (2.48) is ≈1.14, so that
2(0)
T
c
3.5. (2.49)
To calculate the temperature dependence of (T ) at low temperatures, T T
c
we rewrite the master equation using its zero-temperature form (equation (2.45)):
ln
(T )
(0)
=−2
∞
0
dξ
ξ
2
+
2
(T )
f (ξ). (2.50)
Here we have replaced the upper limit in the integral for infinity which is justified
because the quasi-particle distribution function falls down exponentially at low
temperatures,
f (ξ) ≈ exp
−
ξ
2
+
2
(T )
T
. (2.51)
Replacing the integration over ξ by the integration over the energy =
ξ
2
+
2
(T ) yields
ln
(T )
(0)
=−2
∞
(T )
d
e
−/T
2
−
2
(T )
. (2.52)
The remaining integral is exponentially small at low temperatures, so that we
can replace (T ) by (0) on the right-hand side and expand ln in powers of
1
(T ) = (T ) − (0) on the left-hand side with the following result:
1
(T ) =−
2π T (0) exp
−
(0)
T
. (2.53)
The temperature correction to the gap appears to be exponentially small at low
temperatures. In the vicinity of T
c
, where (T
c
− T )/T
c
1, the whole gap is
small compared with the temperature. However, a direct expansion in powers of
cannot be applied in equation (2.23), because every term of such an expansion
would render a divergent integral. Instead we use
tanh x
x
=
∞
n=−∞
1
x
2
+[π(n + 1/2)]
2
(2.54)
BCS gap, critical temperature and single-electron tunnelling
43
so that
1
λ
= 2T
n
ω
D
0
dξ
ξ
2
+ ω
2
n
+
2
(T )
(2.55)
where ω
n
= π T (2n + 1) are the so-called Matsubara frequencies, n =
0, ±1, ±2,.... The last equation can be expanded in powers of (T ) as
ln
T
c
T
= 2
2
(T )T
c
n
∞
0
dξ
(ξ
2
+ ω
2
n
)
2
. (2.56)
Calculating the integral over ξ and the sum over n (appendix B, equation (B.27))
we obtain
(T ) = π T
c
8
7ζ(3)
1/2
1 −
T
T
c
≈ 3.06T
c
1 −
T
T
c
. (2.57)
There is a discontinuity in the temperature derivative of (T ) at T
c
which leads
to a jump of the specific heat (section 2.6).
The gap can be measured directly in tunnelling experiments where one
applies voltage V to a thin dielectric layer between the normal metal and the
superconductor (figure 2.3) [37]. The current running through the dielectric is
proportional to the number of electrons tunnelling under the barrier per second.
The electron, tunnelling from the normal metal, becomes a quasi-particle in the
superconductor. Applying the Fermi–Dirac golden rule, we obtain the transition
rate as
I (V )
k(ξ
k
<0),k
T
2
kk
δ(
k
− ξ
k
− eV). (2.58)
The matrix element T
kk
is almost independent of the momentum k in the
normal metal and of k
in the superconductor, if the voltage is not very high
eV ∼ µ.Theδ-function in equation (2.58) takes into account the difference
eV in the normal and superconducting chemical potentials. Replacing the sum by
the integral we obtain
I (V )
eV
−∞
dξ
+∞
−∞
dξ
δ
ξ
2
+
2
(T ) − ξ
. (2.59)
Then the conductance σ = dI/dV is found:
σ
+∞
−∞
dξ
δ
ξ
2
+
2
(T ) − eV
. (2.60)
Calculating the remaining integral, we obtain
σ
σ
N
=
eV
(eV)
2
−
2
(T )
(2.61)
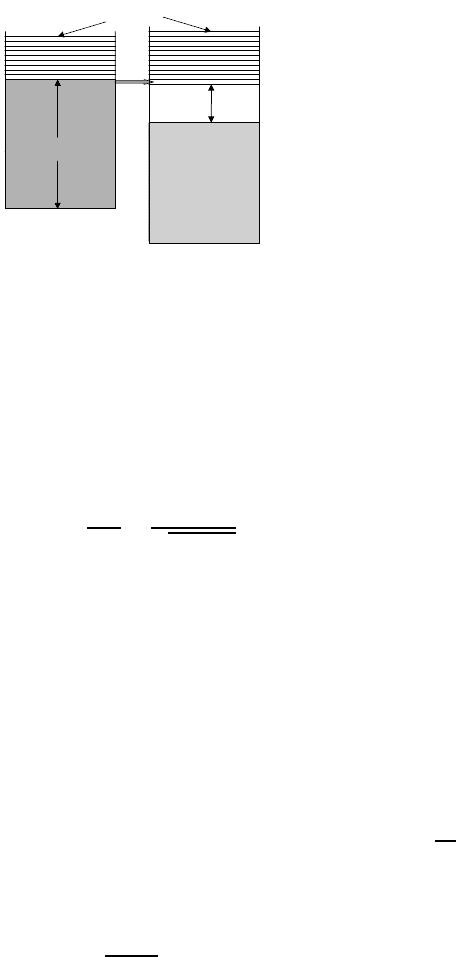
44
Weak coupling theory
µ
2∆
1
6
(PSW\OHYHOV
,
Figure 2.3. Tunnelling from the normal metal (N) to the superconductor (S) through a
dielectric barrier. Shaded areas correspond to occupied states.
where σ
N
is the normal state conductance of the barrier above T
c
.
There is no current if |eV | <because there are no states inside the
gap in the superconductor (figure 2.3). Just above the threshold, eV = , the
conductance has a maximum because the quasi-particle density of states ρ()
diverges at = ,
ρ() ≡
∂|ξ |
∂
=
√
2
−
2
. (2.62)
The typical experimental ratio σ/σ
N
as a function of the voltage and the
temperature follows the BCS prediction (2.61) rather well in conventional
superconductors.
2.5 Isotope effect
The origin of the electron–electron attraction in superconductors can be tested
by isotope substitution, when an ion mass M is varied without any change of
the electronic configuration of the ion. There are two parameters in the BCS
expression for T
c
(equation (2.48)) which depend on the mechanism of the
interaction. The characteristic phonon frequency ω
D
is proportional to 1/
√
M
as a frequency of any harmonic oscillator. However, the coupling constant λ is
independent of the ion mass (section 3.3). Hence, the isotope exponent is found
as
α =−
dlnT
c
dlnM
= 0.5. (2.63)
In fact, the isotope exponent α could be lower than 0.5 in a BCS superconductor
because of the Coulomb repulsion and the anharmonicity of phonons. But, in
any case, the finite value of α measured experimentally proves that phonons are

Heat capacity
45
involved in the pairing mechanism. The isotope effect has been observed in many
conventional superconductors and in high-temperature superconductors (Part II).
2.6 Heat capacity
Only the electrons near the Fermi surface can absorb heat in a metal because of
the Pauli principle. The number of these electrons is proportional to temperature.
Therefore, their specific heat C
e
in the normal state is linear as the function of
temperature (appendix B). The temperature dependence of C
e
changes drastically
in the superconducting state due to the gap. The quasi-particle energies depend on
the temperature in the self-consistent BCS approximation which should be taken
into account in the calculations of temperature derivatives of the thermodynamic
potential. We apply the definition of the specific heat as C
e
= T dS/dT ,where
the quasi-particle entropy is defined as
S =−ln P(U
Q
, N). (2.64)
Here P(U
Q
, N) = Z
−1
e
−βU
Q
is the statistical probability of finding the Fermi
gas of N quasi-particles with energy U
Q
(appendix B),
U
Q
=
k
k
(n
kα
+ n
kβ
) (2.65)
where n
kα,β
= 0, 1 are the quasi-particle occupation numbers; and
Z =
k
[1 +e
β
k
]
2
(2.66)
is the quasi-particle grand partition function. Here we take into account the
fact that the quasi-particle chemical potential is zero. Calculating the statistical
average in equation (2.64), we obtain the entropy of the ideal Fermi gas of quasi-
particles as
S =−2
k
[ f
k
ln f
k
+ (1 − f
k
) ln(1 − f
k
)] (2.67)
where the distribution function f
k
=n
kα
=n
kβ
is defined in equation (2.22).
The temperature derivative of the distribution function includes the derivative of
k
as
d f
k
dT
= f
k
(1 − f
k
)
k
T
2
−
1
T
d
k
dT
so that
C
e
= 2
k
f
k
(1 − f
k
)
2
k
T
2
−
k
T
d
k
dT
. (2.68)
