Alexandrov A.S.,Theory of Superconductivity - From Weak to Strong Coupling
Подождите немного. Документ загружается.

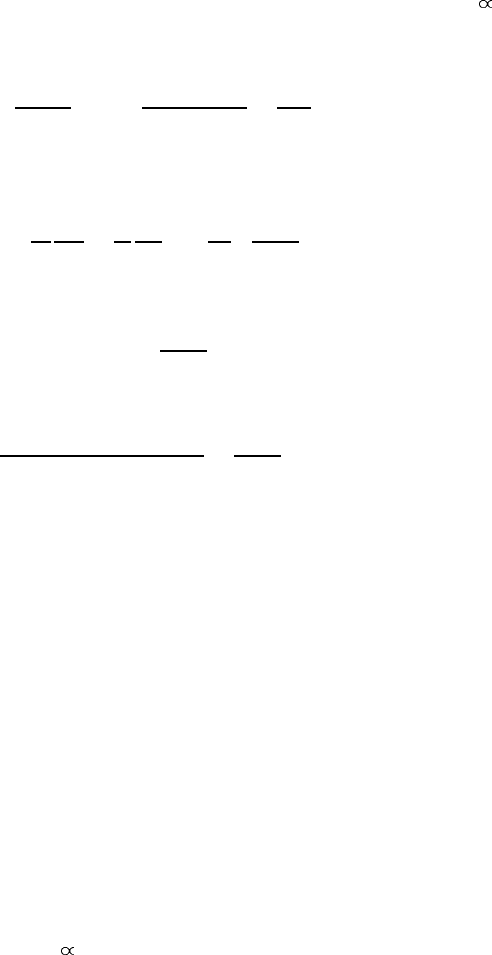
46
Weak coupling theory
At low temperatures, the number of quasi-particles is exponentially small f
k
e
−(0)/T
and so is the specific heat (equation (2.68)). Above T
c
,
k
=|ξ| and we
obtain C
e
= C
N
, where
C
N
=
N(E
F
)
T
2
∞
0
dξ
ξ
2
cosh
2
(ξ/2T )
=
2π
2
3
N(E
F
)T (2.69)
as expected for the ideal Fermi gas (appendix B). However, just below T
c
,the
second term in the brackets of equation (2.68) appears to be finite:
k
T
d
k
dT
=
T
d
dT
=−
π
2
2
8
7ζ(3)
(2.70)
and the specific heat has a discontinuity,
C
e
= C
N
+
8π
2
7ζ(3)
N(E
F
)T
c
(2.71)
if T = T
c
− 0. Here ζ(3) 1.202. The relative value of the jump is
C
e
(T
c
− 0) − C
e
(T
c
+ 0)
C
e
(T
c
+ 0)
=
12
7ζ(3)
1.43 (2.72)
which agrees with the value measured in many conventional superconductors.
The phase transition turns out to be second order as in the GL phenomenology
(chapter 1).
2.7 Sound attenuation
The interaction of ultrasound waves with electrons is described by the following
Hamiltonian:
H
int
= V (q)e
iνt
k,s
c
†
ks
c
k−qs
+ H.c. (2.73)
where q = ν/s and ν are the wavevector and frequency of the sound, respectively
(s is the sound velocity), V (q) is proportional to the sound amplitude and H.c. is
the Hermitian conjugate.
Applying the Bogoliubov transformation, we obtain four terms in the
interaction (2.73). Two of them correspond to the annihilation and creation of
two different quasi-particles and the other two correspond to their scattering. The
sound frequency is low (ν T
c
) and only the scattering terms are relevant:
H
int
k
M
(−)
kq
(α
†
k
α
k−q
+ β
†
k
β
k−q
) (2.74)
where
M
(−)
kq
= u
k
u
k−q
− v
k
v
k−q
(2.75)

Sound attenuation
47
77
F
1RUPDOL]HG
UHVSRQVH
Figure 2.4. Temperature dependence of sound attenuation and thermal conductivity (1)
compared with the nuclear spin relaxation rate (2).
is a so-called coherence factor.
The rate of the sound absorption is given by the Fermi–Dirac golden rule as
W
abs
k
[M
(−)
kq
]
2
f
k−q
(1 − f
k
)δ(
k−q
−
k
+ ν) (2.76)
and the emission rate is
W
emi
k
[M
(−)
kq
]
2
f
k−q
(1 − f
k
)δ(
k−q
−
k
− ν). (2.77)
The sound attenuation , which is the difference between these two rates, is given
by
k
[M
(−)
kq
]
2
( f
k
− f
k−q
)δ(
k−q
−
k
− ν). (2.78)
If ν T,,we have f
k
− f
k−q
≈ ν∂ f/∂. Replacing the integration over k and
over the angle between k and q by the integration over ξ = ξ
k
and ξ
= ξ
k−q
,
respectively, we obtain
−
dξ
dξ
[u(ξ)u(ξ
) − v(ξ)v(ξ
)]
2
∂ f
∂
δ( −
) (2.79)
where =
ξ
2
+
2
and
=
ξ
2
+
2
. Only transitions with ξ = ξ
contribute to the integral over ξ
, so that
−
∞
d
∂ξ
∂
2
[u
2
(ξ) − v
2
(ξ)]
2
∂ f
∂
. (2.80)
Here we can see that the large density of quasi-particle states ∂|ξ |/∂ =
/
√
2
−
2
is cancelled by the small coherence factor in the integral in (2.80) as
−
∞
d
2
−
2
2
−
2
∂ f
∂
=
1
exp(/T ) + 1
. (2.81)

48
Weak coupling theory
The sound attenuation in the superconducting state depends exponentially on
temperature (figure 2.4). Using its ratio to the normal-state attenuation,
s
n
=
2
exp((T )/T ) + 1
(2.82)
one can measure the temperature dependence of the BCS gap.
2.8 Nuclear spin relaxation rate
The measurement of the linewidth of the nuclear magnetic resonance (NMR) is
another powerful method of determining (T ). The linewidth depends on the
inverse time of the relaxation of nuclear magnetic moment due to the spin-flip
scattering of carriers off nuclei, 1/T
1
. This scattering is described by the hyperfine
interaction of the nucleus with the electron spin:
H
int
k,k
c
†
k
↓
c
k↑
+ H.c. (2.83)
The NMR frequency is very small and the spin-flip scattering is practically
elastic. That is why only the scattering of quasi-particles contribute to 1/T
1
as in
the case of sound attenuation,
H
int
k
M
(+)
kk
(β
†
k
α
k
+ α
†
k
β
k
). (2.84)
However, here the coherence factor
M
(+)
kk
= u
k
u
k
+ v
k
v
k
(2.85)
is different. Applying the Fermi–Dirac golden rule, we obtain
1/T
1
k,k
[M
(+)
kk
]
2
( f
k
− f
k
)δ(
k
−
k
− ν) (2.86)
ν → 0. Replacing the sums by the integrals yields a divergent integral,
1/T
1
−T
∞
d
2
+
2
2
−
2
∂ f
∂
. (2.87)
In fact, the divergency is cut by some damping of excitations τ
−1
, for example
due to the inelastic electron–phonon scattering. Above T
c
, where = 0, the
relaxation rate is proportional to T . This linear temperature dependence of 1/ T
1
in a normal metal is known as the Korringa law. It has the same origin as the
linear specific heat. Both are due to the Pauli principle. Only electrons in a
narrow energy region around the Fermi surface can exchange their spin with
Thermal conductivity
49
nuclei and absorb heat. Well below T
c
, the NMR relaxation rate is exponentially
small because of the gap:
1/T
1
e
−/T
ln(τ ) (2.88)
as in sound attenuation. However, just below T
c
, it has a maximum (see
figure 2.4). The maximum in 1/T
1
is one of the most interesting and important
features of BCS theory. This result is distinctly different from the result for sound
attenuation. They differ because the coherence factors are different:
M
(+,−)
= (uu
± vv
). (2.89)
A simple energy-gap form of a two-fluid model could account for the drop in
the sound attenuation but not for the rapid rise of 1/T
1
just below T
c
.The
observation by Hebel and Slichter [38] of the peak in 1/T
1
was one of the first
in the body of evidence for the detailed nature of the pairing correlations in BCS
superconductors.
2.9 Thermal conductivity
Important information about the excitation spectrum of the superconducting state
can also be obtained from thermal conductivity [39]. Quasi-particles contribute
to heat transfer in a superconductor. Their contribution Q to the heat flow is
determined by the deviation
˜
f of the distribution function from the equilibrium,
Q =
k
˜
f v
k
(2.90)
where v = ∂
k
/∂ k is the quasi-particle group velocity. The distribution function
obeys the Boltzmann equation, which for a small deviation from the equilibrium
has the form:
v ·
∂ f
∂ r
−
∂
k
∂ r
·
∂ f
∂ k
=−
˜
f
τ
s
tr
(2.91)
where the transport relaxation rate for elastic scattering is obtained using the
Fermi–Dirac golden rule:
1
τ
s
tr
=
|ξ|
1
τ
n
tr
. (2.92)
In the superconducting state, the transport relaxation rate is diminished by a factor
|ξ|/ < 1 compared with that in the normal state (1/τ
n
tr
) because of the square
of the coherence factor M
(−)
in the probability of scattering. The second term
on the left-hand side of the Boltzmann equation accounts for the driving force,
which acts on a quasi-particle due to the temperature dependence of its energy,
=
ξ
2
+|(T (r)|
2
. The solution of equation (2.91) is
˜
f = τ
n
tr
2
T |ξ|
∂ f
∂
v · ∇T . (2.93)

50
Weak coupling theory
Substituting it into equation (2.90) yields the thermal conductivity K =
|Q|/|∇T | as
K
s
−
1
T
∞
d
2
∂ f
∂
. (2.94)
Hence, the ratio to the normal-state thermal conductivity is
K
s
K
n
=
∞
/2T
dxx
2
/cosh
2
(x )
∞
0
dxx
2
/ cosh
2
(x )
. (2.95)
The normalized thermal conductivity (equation (2.95)) drops exponentially with
the temperature lowering below T
c
just like sound attenuation (figure 2.4).
2.10 Unconventional Cooper pairing
In BCS theory electrons are paired with the opposite momenta on the Fermi
surface and the opposite spins. The simple approximation for the pairing potential
(equation (2.6)) leads to the momentum-independent gap
k
= , which is
uniform along the Fermi surface. This is an s-wave order parameter because
the pair wavefunction is isotropic in real space. It depends only on the distance
between two correlated electrons. BCS theory describes an anisotropic Cooper
pairing with non-zero orbital momentum of pairs l = 0 as well, if the potential
allows for such pairing [40]. In the general case, the mean-field Hamiltonian is
˜
H =
k,s=↑,↓
ξ
k
c
†
ks
c
ks
+
1
2
s
(
ss
k
c
†
ks
c
†
−ks
+ H.c.)
(2.96)
whereweomitthec-number term, which does not contain fermionic operators.
The order parameter should be antisymmetric:
ss
k
=−
ss
−k
(2.97)
according to the Pauli exclusion principle. Applying the Bogoliubov
transformation, the master equation for any pairing potential V (k, k
) takes the
following form:
ss
k
=−
k
V (k, k
)
ss
k
2
k
(1 − 2 f
k
). (2.98)
Let us assume that V (k, k
) depends on the value of the momentum transfer
q =|k − k
|, which is the case for an isotropic system. In BCS theory,
the states near the Fermi surface contribute to the sum in equation (2.97) and
q ≈ 2
1/2
k
F
√
1 − cos
,where
is the angle between k and k
.Thenall
functions in the master equation depend on the angles of k and k
with the absolute

Unconventional Cooper pairing
51
values of the momenta equal to the Fermi momentum, |k|=|k
|=k
F
. We can
expand the order parameter and the potential in the polynomial series:
ss
k
=
∞
l=0
(l)P
l
(cos ) (2.99)
V (q) =
∞
l=0
V (l)P
l
(cos
)
where P
l
(cos ) are the Legendre polynomials,
P
l
(x ) =
1
2
l
l!
d
l
dx
l
(x
2
− 1)
l
(2.100)
which are orthogonal and normalized as
1
−1
dxP
l
(x )P
l
(x ) =
2δ
ll
2l + 1
. (2.101)
This expansion is instrumental due to the summation theorem:
P
l
(cos
) = P
l
(cos )P
l
(cos
)
+ 2
l
m=1
(l − m)!
(l + m)!
P
m
l
(cos )P
m
l
(cos
) cos[m(φ − φ
)]
(2.102)
where P
m
l
(x ) are associated Legendre functions defined as
P
m
l
(cos ) = sin
m
d
m
P
l
(cos )
(dcos)
m
and
is the angle between any two directions determined by the spherical angles
(, φ) and (
,φ
), respectively. Substitution of the series into the master
equation yields a system of coupled nonlinear equations for the amplitudes (l).
These equations are linearized and decoupled at T = T
c
. Using the orthogonality
of the Legendre polynomials and the summation theorem (equation (2.102)), we
obtain, for an isotropic system with parabolic energy dispersion,
(l) =−
V (l)N(E
F
)
2l + 1
(l)
ω
D
0
dξ tanh(ξ/2T
c
)
ξ
. (2.103)
Then the critical temperature
T
c
=
2e
C
ω
D
π
exp
−
1
λ
l
∗
(2.104)

52
Weak coupling theory
where λ
l
∗
≡|V (l
∗
)|N(E
F
)/(2l
∗
+ 1) for negative V (l
∗
). The solution of
equation (2.103) is trivial: (l) = 0foralll except l = l
∗
with a maximum
value of λ
l
∗
and negative V (l
∗
). Hence, if the Fourier transform of the pairing
potential has an attractive component with l = 0, the system condenses into
the state with non-zero orbital momentum of the pair wavefunction. The single-
particle gap,
k
P
l
(cos ), has nodes on the Fermi surface if l = 0. It is odd for
l = 1, 3, 5,...and even for even l,
−k
= (−1)
l
k
. The order parameter,
k
,is
proportional to the Fourier transform of the pair wavefunction. The change in sign
of k corresponds to the permutation of real-space coordinates of the two fermions
of the pair. According to the Pauli exclusion principle, the total wavefunction
of the pair should change its sign after the permutation of both the orbital and
spin coordinates of two fermions. Hence, the spin component of the paired state
with an odd orbital momentum should be symmetric under the permutation of the
spin coordinates of two particles, while the spin component of even orbital states
should be antisymmetric. Therefore, the even l states (s, d,...)are singlets (total
spin S is zero) and the odd l states ( p, f,...)are triplets (S = 1).
2.11 Bogoliubov equations
The Bogoliubov transformation of the BCS Hamiltonian can be readily
generalized for inhomogeneous superconductors. Let us introduce field operators
(appendix C)
s
(r) =
k
c
ks
exp(ik · r). (2.105)
Here and further on, we take the volume of the system as V = 1. Then the BCS
Hamiltonian can be written as follows:
˜
H =
dr
s
†
s
(r)
ˆ
h(r)
s
(r) + (r)
†
↑
(r)
†
↓
(r) +
∗
(r)
↓
(r)
↑
(r)
(2.106)
where
ˆ
h(r) =−
[∇ + ie A(r)]
2
2m
+U(r) − µ (2.107)
is the one-electron Hamiltonian in the external magnetic ( A(r)) and electric
(U(r)) fields. We apply the effective mass (m) approximation for the band
dispersion (see appendix A) and drop c-number terms in the total energy. The
coordinate-dependent order parameter is given by
(r) =−2E
p
↓
(r)
↑
(r). (2.108)
Superfluid properties of inhomogeneous superconductors can be studied by the
use of the Bogoliubov equations, fully taking into account the interaction of quasi-

Bogoliubov equations
53
particles with the condensate. To derive these equations, we introduce the time-
dependent Heisenberg operators (appendix D) as
ψ
s
(r, t) = e
i
˜
Ht
s
(r)e
−i
˜
Ht
. (2.109)
The equations of motion for these operators are readily derived:
i
∂ψ
↑
(r, t)
∂t
=−[
˜
H,ψ
↑
(r, t)]
=
ˆ
h(r)ψ
↑
(r, t) + (r)ψ
†
↓
(r, t) (2.110)
and
−i
∂ψ
†
↓
(r, t)
∂t
=[
˜
H,ψ
†
↓
(r, t)]
=
ˆ
h
∗
(r)ψ
†
↓
(r, t) −
∗
(r)ψ
↑
(r, t). (2.111)
Here we have applied commutation relations for the field operators:
{
s
(r),
†
s
(r
)}=
k,k
{c
ks
, c
†
k
s
}exp[ik · r − ik
· r
)
= δ
ss
k
exp[ik · (r − r
)]=δ
ss
δ(r − r
)
and
[
†
↑
(r
)
†
↓
(r
),
↑
(r)]= −δ(r − r
)
†
↓
(r) (2.112)
[
†
↑
(r
)
↑
(r
),
↑
(r)]= −δ(r − r
)
†
↑
(r).
The linear Bogoliubov transformation of ψ-operators has the form
ψ
↑
(r, t) =
n
[u
n
(r, t)α
n
+ v
∗
n
(r, t)β
†
n
] (2.113)
ψ
↓
(r, t) =
n
[u
n
(r, t)β
n
− v
∗
n
(r, t)α
†
n
] (2.114)
where α
n
and α
†
n
are the fermion operators, which annihilate and create quasi-
particles in a quantum state n. Using this transformation in equations (2.110)
and (2.111), we obtain two coupled Schr¨odinger equations for the wavefunctions
u(r, t) and v(r, t):
i
d
dt
u(r, t) =
ˆ
h(r)u(r, t) − (r)v(r, t), (2.115)
−i
d
dt
v(r, t) =
ˆ
h
∗
(r)v(r, t) +
∗
(r)u(r, t).

54
Weak coupling theory
There is also the sum rule,
n
[u
n
(r, t)u
∗
n
(r
, t) + v
n
(r, t)v
∗
n
(r
, t)]=δ(r − r
) (2.116)
which retains the Fermi commutation relations for all operators. When the
magnetic and electric fields are stationary, these equations are reduced to the
steady-state ones:
n
u
n
(r) =
−
[∇ + ie A(r)]
2
2m
+U(r) − µ
u
n
(r) − (r)v
n
(r) (2.117)
n
v
n
(r) =−
−
[∇ − ie A(r)]
2
2m
+U(r) − µ
v
n
(r) −
∗
(r)u
n
(r).
Using the same transformation, the quantum and statistical averages in
equations (2.108) yield the self-consistent equation for the order parameter:
(r) =−2E
p
n
u
n
(r)v
∗
n
(r)(1 −2 f
n
) (2.118)
where f
n
=α
†
n
α
n
= β
†
n
β
n
= (1 + exp
n
/T )
−1
is the equilibrium quasi-
particle distribution in the quantum states n with energy
n
. We can readily
solve the set of Bogoliubov equations (2.117) in the homogeneous case, when
A(r) = U (r) = 0. In this case the excitation wavefunctions are plane waves,
u
k
(r) = u
k
e
ik·r
(2.119)
v
k
(r) = v
k
e
ik·r
(2.120)
and the order parameter (r) is r-independent, (r) = . Substituting
equations (2.119) and (2.120) into equations (2.117), we obtain
k
u
k
= ξ
k
u
k
− v
k
(2.121)
k
v
k
=−ξ
k
v
k
−
∗
u
k
(2.122)
and, from equation (2.116),
|u
k
|
2
+|v
k
|
2
= 1. (2.123)
As a result, we find
|u
k
|
2
=
1
2
1 +
ξ
k
k
(2.124)
|v
k
|
2
=
1
2
1 −
ξ
k
k
(2.125)
u
k
v
∗
k
=−
2
k
. (2.126)

Landau criterion and gapless superconductivity
55
The elementary excitation energy is
k
=
ξ
2
k
+||
2
(2.127)
as it should be (see equation (2.18)), where the gap is found using the master
equation,
= 2E
p
k
2
k
(1 − 2 f
k
). (2.128)
2.12 Landau criterion and gapless superconductivity
The Bogoliubov equations are coupled nonlinear integra-differential equations.
They are mathematically transparent but the analytical solution is possible only in
a few simple cases. As an example, we consider a uniform flow with the superfluid
velocity v
s
. This state is described by an oscillating complex order parameter
(r) = exp(2iq · r) (2.129)
where 2q = 2mv
s
is the centre-of-mass momentum of the Cooper pair, and is
the real amplitude. Let us examine how the flow destroys superconductivity. If
the flow is uniform, the system remains translation invariant and the momentum
k is a quantum number. The solution has the form
u
n
(r) = u
k
exp[i(k + q) · r] (2.130)
v
n
(r) = v
k
exp[i(k − q) · r]
where the coefficients u
k
and v
k
are found from
(E
k
− ξ
k+q
)u
k
+v
k
= 0 (2.131)
(E
k
+ ξ
k−q
)v
k
+u
k
= 0.
Taking into account the normalization condition u
2
k
+ v
2
k
= 1, we obtain
u
2
k
,v
2
k
=
1
2
1 ±
ξ
k+q
+ ξ
k−q
2
k
(2.132)
u
k
v
k
=−
2
k
and the excitation spectrum
E
k
=
ξ
k+q
− ξ
k−q
2
+
(ξ
k+q
+ ξ
k−q
)
2
4
+
2
. (2.133)
If we apply the Landau criterion (1.117) to the spectrum equation (2.133), the
critical velocity will be v
c
= /k
F
. Hence, we can keep only the terms of the
