Alexandrov A.S.,Theory of Superconductivity - From Weak to Strong Coupling
Подождите немного. Документ загружается.


86
Intermediate-coupling theory
can be done in a compact form by introducing the matrix GF [49]:
s
(k,τ) =−
T
τ
c
k↑
(τ )c
†
k↑
T
τ
c
k↑
(τ )c
−k↓
T
τ
c
†
−k↓
(τ )c
†
k↑
T
τ
c
†
−k↓
(τ )c
−k↓
(3.72)
and the matrix self-energy
ˆ
(k,ω
n
) = (
(0)
(k,ω
n
))
−1
−
−1
s
(k,ω
n
) (3.73)
where
(0)
(k,ω
n
) = (iω
n
τ
0
−ξ
k
τ
3
)
−1
is the normal-state matrix GF. Here τ
0,1,2,3
are the Pauli matrices,
τ
0
=
10
01
τ
1
=
01
10
τ
2
=
0 −i
i 0
τ
3
=
10
0 −1
.
The generalized equation for the matrix
ˆ
is given by the same diagram as in the
normal state (figure 3.5) but replacing ˜γ(q) by ˜γ(q)τ
3
and the integral over ω by
the sum over the Matsubara frequencies:
ˆ
(k,ω
n
) =−
T
(2π)
3
N
ω
n
dq ˜γ
2
(q) ˜ω
q
τ
3 s
(k − q,ω
n
)τ
3
(q,ω
n
− ω
n
).
(3.74)
Here the temperature GF of phonons is given by
(q,
n
) =−
˜ω
2
q
2
n
+˜ω
2
q
(3.75)
where
n
= 2π Tn are the Matsubara frequencies for bosons. The most
important difference between equation (3.74), figure 3.7, and the normal state
equation (3.54), figure 3.5, is a finite value of the anomalous GF in the
self-consistent solution. If we replace
s
by
(0)
on the right-hand side of
equation (3.74), we do not find any anomalous
. Hence, there are no anomalous
averages and no phase transition in the second or in any finite order of the
perturbation theory. However, if we solve equation (3.74) self-consistently, we
find the finite anomalous averages.
The diagrams in figure 3.7 are expressed in analytical form as a set
of Eliashberg equations, similar to Gor’kov’s equations (2.186) but with a
microscopically determined pairing potential. They include all non-crossing
(‘ladder’) diagrams in every order of the perturbation theory. For simplicity, let
us consider a momentum-independent ˜γ
2
(q) ˜ω
q
as in the previous section and
approximate the phonon GF in equation (3.74) as
(q,
n
) ≈−1 (3.76)
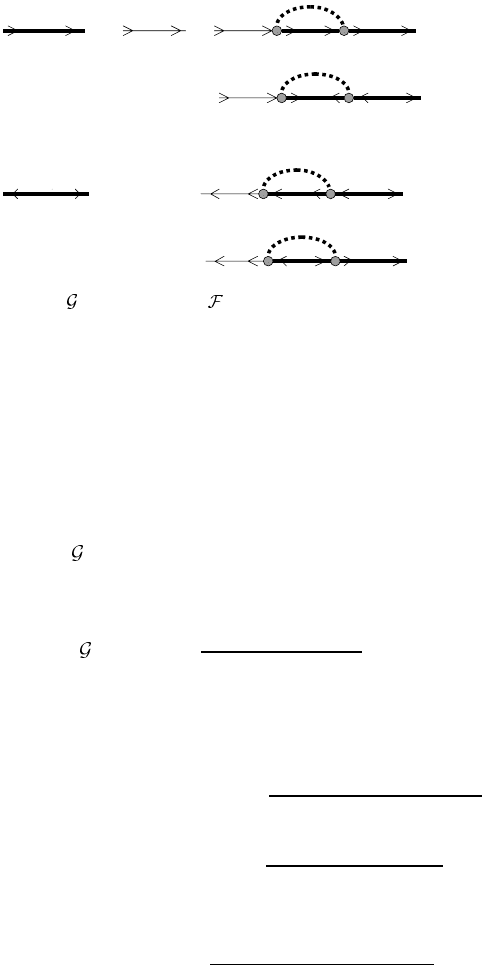
Eliashberg equations
87
*
)
Figure 3.7. Normal and anomalous
+
GFs of the BCS superconductor in the
Eliashberg theory.
if |
n
| <ω
D
, and zero otherwise.
ˆ
is the sum of three Pauli matrices τ
0,1,3
with the coefficients (1 − Z )iω
n
, and χ, respectively, which in this case are
functions of frequency alone,
ˆ
(k,ω
n
) = i(1 − Z )ω
n
τ
0
+ τ
1
+ χτ
3
(3.77)
and
−1
s
(k,ω
n
) = iZ ω
n
τ
0
− τ
1
−
˜
ξ
k
τ
3
. (3.78)
Transforming the inverse matrix (equation (3.78)) back into the original one yields
s
(k,ω
n
) =−
iZω
n
+ τ
1
+
˜
ξ
k
τ
3
Z
2
ω
2
n
+
˜
ξ
2
k
+||
2
(3.79)
where
˜
ξ
k
= ξ
k
+ χ. Substituting equations (3.76) and (3.79) into the master
equation (3.74) leads to the following simplified Eliashberg equations:
[1 − Z(ω
n
)]iω
n
=−λT
∞
−∞
d
˜
ξ
ω
n
(ω
D
−|ω
n
− ω
n
|)iω
n
Z
Z
2
ω
2
n
+
˜
ξ
2
+||
2
(3.80)
χ(ω
n
) =−λT
ω
n
∞
−∞
d
˜
ξ
(ω
D
−|ω
n
− ω
n
|)
˜
ξ
Z
2
ω
2
n
+
˜
ξ
2
+||
2
(3.81)
and
(ω
n
) = λT
ω
n
∞
−∞
d
˜
ξ
(ω
D
−|ω
n
− ω
n
|)(ω
n
)
Z
2
ω
2
n
+
˜
ξ
2
+||
2
. (3.82)
We can satisfy equations (3.80) and (3.81) with Z = 1andχ = 0. In the last
equation, we extend the summation over frequencies to infinity but cut the integral

88
Intermediate-coupling theory
over |
˜
ξ| at ω
D
. Then applying equation (2.54) for tanh yields the familiar BCS
equation for the order parameter,
1 = λ
ω
D
0
d
˜
ξ
˜
ξ
2
+||
2
tanh
˜
ξ
2
+||
2
2T
. (3.83)
Hence the Migdal–Eliashberg theory reproduces the BCS results, if a similar
approximation for the attraction between electrons is adopted. The critical
temperature and the BCS gap are adiabatically small (
ω
D
) compared with
the Fermi energy and we could worry about the adiabatically small crossing
diagrams in figure 3.6, which are neglected in the master equation, (3.74).
However, the BCS state is essentially the same as the normal state outside the
narrow momentum region around the Fermi surface. The outside regions mainly
contribute to the integrals of the crossing diagrams, which makes them small as
in the normal state. As a result, the vertex corrections are small and Migdal’s
theorem holds in the BCS state as well.
Within a more general consideration the master equation (3.74) takes
properly into account the phonon spectrum, retardation and realistic matrix
elements of the electron–phonon interaction in metals [50–52]. The important
feature of the intermediate-coupling theory is the explicit frequency dependence
of the order parameter (ω
n
), which is transformed into the energy-dependent
gap in the quasi-particle DOS as
ρ() =
2
−|()|
2
. (3.84)
The DOS (equation (3.84)) can be measured in the tunnelling experiments
(section 2.4). As the gap depends on the phonon spectrum, phonons affect the
tunnelling I –V characteristics. Let us define the phonon density of states
F(ω) =
1
N
qν
δ(ω −˜ω
qν
) (3.85)
and the so-called Eliashberg function α
2
F,
α
2
(ω)F(ω) =
1
N(E
F
)N
k,k
˜γ
2
(k − k
,ν)˜ω
2
k−k
,ν
δ(ω −˜ω
k−k
,ν
)δ(ξ
k
)δ(ξ
k
)
(3.86)
which is an average over the Fermi surface of the interaction matrix element
squared multiplied by the phonon spectral density. The quasi-particle DOS
(equation (3.84)) can be obtained in a direct fashion using the tunnelling
conductivity of the superconducting tunnel junctions. Then the function α
2
F
can be calculated to fit the experimental energy dependence of the gap ()
[54] and compared with the phonon density of states measured independently,
Coulomb pseudopotential
89
for example, in neutron scattering experiments. The comparison shows that
frequency dependence of the Eliashberg function and the phonon density of
states are similar in many low-temperature superconductors with a weak or
intermediate electron–phonon coupling, for example in lead. The observation
of the characteristic phonon frequencies in tunnelling (usually in the second
derivative of the current versus voltage) and the isotope effect are used to verify
the phonon-mediated pairing mechanism.
3.5 Coulomb pseudopotential
The theory of superconductivity has to take account of the Coulomb repulsive
correlations between electrons, which might be much stronger than the attraction
induced by phonons. There is no adiabatic parameter for this interaction because
the electron plasma frequency ω
e
=
4πn
e
e
2
/m
e
has about the same order of
magnitude as the Fermi energy in metals. Nevertheless, we can account for the
Coulomb repulsion in the same fashion as for the electron–phonon interaction but
replacing ˜γ
2
(q) ˜ω
q
D(q,ω
n
− ω
n
) in equation (3.74) by the Fourier component
of the Coulomb potential V
c
. The Coulomb interaction is non-retarded for
frequencies less than ω
e
. Then the kernel K (ω
n
− ω
n
) in the BCS equation,
(ω
n
) = T
dξ
ω
n
K (ω
n
− ω
n
)
(ω
n
)
ω
2
n
+ ξ
2
+|(ω
n
)|
2
(3.87)
can be parametrized as
K (ω
n
− ω
n
) = λ(ω
D
−|ω
n
− ω
n
|) − µ
c
(ω
e
−|ω
n
− ω
n
|) (3.88)
where µ
c
= V
c
N(E
F
).AtT = T
c
, we neglect second and higher powers of the
order parameter and integrating over ξ obtain
(ω
n
) = π T
c
ω
n
K (ω
n
− ω
n
)
(ω
n
)
|ω
n
|
. (3.89)
Let us adopt the BCS-like approximation of the kernel:
K (ω
n
− ω
n
) λ(2ω
D
−|ω
n
|)(2ω
D
−|ω
n
|)
− µ
c
(2ω
e
−|ω
n
|)(2ω
e
−|ω
n
|)
and replace the summation in equation (3.89) by the integral:
π T
c
≈
∞
π T
c
dω (3.90)
because T
c
ω
D
ω
e
. Then the solution is found in the form
(ω) =
1
(2ω
D
−|ω|) +
2
(2ω
e
−|ω|)(|ω|−2ω
D
) (3.91)
90
Intermediate-coupling theory
with constant but different values of the order parameter
1
and
2
below and
above the cut-off energy 2ω
D
, respectively. Substituting equation (3.91) into
equation (3.89) yields the following equations for
1,2
:
1
1 − (λ −µ
c
) ln
2ω
D
π T
c
+
2
µ
c
ln
ω
e
ω
D
= 0 (3.92)
1
µ
c
ln
2ω
D
π T
c
+
2
1 + µ
c
ln
ω
e
ω
D
= 0. (3.93)
A non-trivial solution of these coupled equations is found, if
T
c
=
2ω
D
π
exp
−
1
λ − µ
∗
c
(3.94)
where
µ
∗
c
=
µ
c
1 + µ
c
ln(ω
e
/ω
D
)
(3.95)
is the so-called Coulomb pseudopotential [53]. This is a remarkable result.
It shows that even a large Coulomb repulsion µ
c
>λdoes not destroy the
Cooper pairs because its contribution is suppressed down to the value about
ln
−1
(ω
e
/ω
D
) 1. The retarded attraction mediated by phonons acts well after
two electrons meet each other. This time delay is sufficient for two electrons to
be separated by a relative distance, at which the Coulomb repulsion is small.
The Coulomb correlations also lead to a damping of excitations of the order
of ξ
2
/µ, which is relevant only in a narrow region around the Fermi surface
|ξ|
ω
D
√
m
e
/M. The damping due to the Fr¨ohlich interaction dominates outside
this region.
Computational analysis of the Eliashberg equations led McMillan [54] to
suggest an empirical formula for T
c
, which works well for simple metals and
their alloys,
T
c
=
ω
D
1.45
exp
−
1.04(1 +λ)
λ −µ
∗
c
(1 + 0.62λ)
. (3.96)
However, in materials with a moderate T
c
20 K (like Nb
3
Sn, V
3
Si and in other
A-15 compounds), the discrepancy between the value of λ, estimated from this
equation and from the first-principle band-structure calculations, exceeds the limit
allowed by the experimental and computation accuracy by several times [55].
In the original papers, Migdal [48] and Eliashberg [36] restricted the
applicability of their approach to the intermediate region of coupling λ<1. With
the typical values of λ = 0.5andµ
∗
c
= 0.14 and with the Debye temperature
as high as ω
D
= 400 K, McMillan’s formula predicts T
c
≈ 2 K, clearly too low
to explain high T
c
values in novel superconductors. One can formally compute
T
c
and the gap using the Eliashberg equations (3.74) also in the strong-coupling
regime λ>1. In particular, Allen and Dynes [56] found that in the extreme
strong-coupling limit (λ 1), the critical temperature may rise as
T
c
≈
ω
D
λ
1/2
2π
. (3.97)

Cooper pairing of repulsive fermions
91
However, the Migdal–Eliashberg theory is based on the assumption that the Fermi
liquid is stable and the adiabatic condition µ ω
D
is satisfied. As we shall later
discuss in chapter 4, this assumption cannot be applied in the strong-coupling
regime and the proper extension of the BCS theory to λ>1 inevitably involves
small polarons and bipolarons.
3.6 Cooper pairing of repulsive fermions
The phenomenon of superconductivity is due to the interaction of electrons with
vibrating ions, which mediates an effective attractive potential V (k, k
)<0in
equation (2.98). In recent years, great attention has been paid to a possibility of
superconductivity mediated by strong electron–electron correlations without any
involvement of phonons. Some time ago, Kohn and Luttinger [57] pointed out
that such possibility exists at least theoretically. They found that a dilute Fermi
gas cannot remain normal down to absolute zero of temperature even in the case
of purely repulsive short-range interaction between the particles. A system of
fermions with purely repulsive short-range forces will inevitably be superfluid at
zero temperature.
To understand what is involved, one should consider the screening of a
charge placed in a metal. It has long been known [58] that if fermions are
degenerate (i.e. their Fermi surface is well defined), the screening produces an
oscillatory potential of the form cos(2k
F
r + ϕ)/r
3
at the distance r from the
charge (here ϕ is a constant) which has attractive regions. Using these regions
of screened interaction, unconventional Cooper pairs can form with non-zero
orbital momentum (section 2.10). Following Kohn and Luttinger, let us consider a
simplified model of spin-
1
2
fermions with a weak short-range repulsive interaction
between them. The critical temperature of unconventional Cooper pairing with
the orbital momentum l is found as (see equation (2.104))
T
c
≈ µ exp
−
1
λ
l
. (3.98)
Here we replaced the Debye temperature by the Fermi energy µ because
the fermion–fermion interaction is non-retarded. The coupling constant λ
l
is
expressed in terms of spherical harmonics V (l) of the Fourier transform of the
interaction potential,
λ
l
≡−
V (l)mk
F
2π(2l + 1)
(3.99)
on condition that V (l) is negative. For simplicity, we choose the repulsive bare
potential as V (r −r
) = U with a positive U, if |r −r
| r
0
, and V (r −r
) = 0,
if |r − r
| > r
0
. We also assume that the gas is diluted, that is the radius of the
potential is small compared with the characteristic wave-length of fermions,
k
F
r
0
1. (3.100)
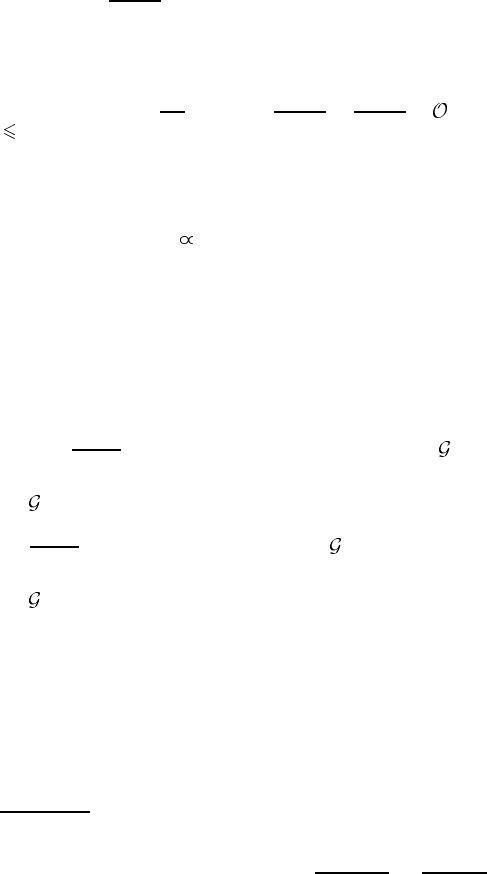
92
Intermediate-coupling theory
It is easy to estimate V (l) for such a potential,
V (l) =
2l + 1
2
π
0
d sin P
l
(cos )V (q) (3.101)
where q
2
= 2k
F
(1 − cos ) is about 2k
F
or less and
V (q) = U
r a
dr exp(iq ·r) ≈
4π
3
Ur
3
0
1 −
(qr
0
)
2
10
+
(qr
0
)
4
40
+
[(k
F
r
0
)
6
]
.
(3.102)
Substituting the Fourier transform (3.102) into equation (3.101), we obtain a
positive V (l) of the order of
V (l)
Ur
3
0
(k
F
r
0
)
2l
. (3.103)
We conclude that the repulsive bare potential does not produce any pairing. Let us
now take screening into account. It is sufficient to consider it perturbatively, if the
potential is weak, U µ. The diagrams contributing to the effective interaction
up to the second order in U are shown in figure 3.8. In the analytical form, the
Fourier transform of the effective interaction of two electrons on the Fermi surface
is given by
˜
V (k, k
) = V (q) −
T
(2π)
3
ω
n
d p [2V
2
(q) − 2V (q)V (k
− p)]
(0)
ω
n
( p,ω
n
)
×
(0)
ω
n
( p + q,ω
n
)
+
T
(2π)
3
ω
n
d p V (k − p)V (k
− p)
(0)
ω
n
( p,ω
n
)
×
(0)
ω
n
( p − k
− k,ω
n
). (3.104)
Because the density is low (equation (3.100)) we can neglect the q-
dependence of V (q) and take V (q) = 4πUr
3
0
/3 ≡ v in the second-order terms of
equation (3.104). Then the diagrams (b)and(c) + (d) cancel each other and the
second term in the right-hand side of equation (3.104) vanishes. The remaining
last term yields the familiar polarization bubble (equation (3.40)) which finally
leads to
˜
λ
l
≡−
˜
V (l)mk
F
2π(2l + 1)
= λ
l
− λ(−1)
l
π
0
d sin P
l
(cos )
1 +
4k
2
F
− q
2
4k
F
q
ln
2k
F
+ q
2k
F
− q
(3.105)
where λ = (ak
F
/π)
2
1. Here the first repulsive term is about
(ak
F
)(k
F
r
0
)
2l
, where a = vm
e
/(2π) is the s-wave scattering amplitude in

Cooper pairing of repulsive fermions
93
D
E
F
G H
I
Figure 3.8. The first (a) and second-order diagrams (b–e) which contribute to the screened
electron–electron interaction. Note that the non-crossing second-order diagram (f) as well
as all higher-order non-crossing diagrams are fully taken into account in the BCS equation
(section 3.4) and should not be included in the irreducible scattering vertex.
the Born approximation. The second ‘polarization’ contribution to effective
interaction is of the order of (ak
F
)
2
. Hence, if the gas parameter is sufficiently
small,
(k
F
r
0
)
2l−3
U
µ
(3.106)
the polarization contribution overcomes direct repulsion for all l
2and
it is attractive. For example, for l = 2 (d-wave pairing), the integral in
equation (3.105) yields
˜
λ
2
= λ
4
105
(8 − 11 ln 2) ≈ 0.015λ. (3.107)
The corresponding critical temperature is
T
c
≈ µ exp
−
1
0.015λ
(3.108)
which is practically zero at any λ<1. The situation is slightly better when
the repulsive potential U is strong (U µ) (i.e. for hard-core spheres) [59].
Partial scattering amplitudes f
l
in a vacuum are of the order of r
0
(k
F
r
0
)
2l
in this
limit. They are small compared with the attractive polarization contribution to the
amplitudes (
r
0
(k
F
r
0
)) starting from l = 1. Hence, at T = 0, hard-core fermions
with repulsive scattering in a vacuum are necessarily in a superfluid p-wave state.
Calculating the integral in equation (3.105) for l = 1, we obtain
˜
λ
1
= λ
2
5
(2ln2− 1) ≈ 0.15λ (3.109)

94
Intermediate-coupling theory
and
T
c
≈ µ exp
−
1
0.15λ
. (3.110)
The Fermi energy could be as large as µ = 10
4
KbutT
c
still remains very low
because λ 1 in the dilute limit.

Chapter 4
Strong-coupling theory
The electron–phonon coupling constant λ is about the ratio of the electron–
phonon interaction energy E
p
to the half-bandwidth D N(E
F
)
−1
(appendix A).
We expect [11] that when the coupling is strong (λ>1), all electrons in the
Bloch band are ‘dressed’ by phonons because their kinetic energy (<D)issmall
compared with the potential energy due to a local lattice deformation, E
p
, caused
by an electron. If phonon frequencies are very low, the local lattice deformation
traps the electron. This self-trapping phenomenon was predicted by Landau [60].
It has been studied in greater detail by Pekar [61], Fr¨ohlich [62], Feynman [63],
Devreese [64] and other authors in the effective mass approximation, which leads
to the so-called large polaron. The large polaron propagates through the lattice
like a free electron but with the enhanced effective mass. In the strong-coupling
regime (λ>1), the finite bandwidth becomes important, so that the effective
mass approximation cannot be applied. The electron is called a small polaron
in this regime. The self-trapping is never ‘complete’, that is any polaron can
tunnel through the lattice. Only in the extreme adiabatic limit, when the phonon
frequencies tend to zero, is the self-trapping complete and the polaron motion
no longer translationally continuous (section 4.2). The main features of the small
polaron were understood by Tjablikov [65], Yamashita and Kurosava [66], Sewell
[67], Holstein [68] and his school [69, 70], Lang and Firsov [71], Eagles [72]
and others and described in several review papers and textbooks [13, 64, 73–76].
The exponential reduction of the bandwidth at large values of λ is one of those
features (section 4.3). The small polaron bandwidth decreases with increasing
temperature up to a crossover region from the coherent small polaron tunnelling
to a thermally activated hopping. The crossover from the polaron Bloch states to
the incoherent hopping takes place at temperatures T ≈ ω
0
/2 or higher, where ω
0
is the characteristic phonon frequency. In this chapter, we extend BCS theory to
the strong-coupling regime (λ>1) with the itinerant (Bloch) states of polarons
and bipolarons.
95
