Alexandrov A.S.,Theory of Superconductivity - From Weak to Strong Coupling
Подождите немного. Документ загружается.


96
Strong-coupling theory
4.1 Electron–phonon and Coulomb interactions in the
Wannier representation
For doped semiconductors and metals with a strong electron–phonon (e–ph)
interaction, it is convenient to transform the Bloch states to the site (Wannier)
states using the canonical linear transformation of the electron operators
(appendix C):
c
i
=
1
√
N
k
e
ik·m
c
ks
(4.1)
where i ≡ (m, s) includes both site m and spin s quantum numbers. In the new
representation, the periodic part of the Hamiltonian (3.17) takes the following
form:
H
e
=
i, j
[T (m − m
)δ
ss
− µδ
ij
]c
†
i
c
j
, (4.2)
where
T (m) =
1
N
k
E
nk
e
ik·m
is the ‘bare’ hopping integral (appendix A). Here i = (m, s) and j = (n, s
).
The electron–phonon interaction and the Coulomb correlations acquire
simple forms in the Wannier representation, if their matrix elements in
the momentum representation depend only on the momentum transfer q,
equation (3.21):
H
e−ph
=
q,ν,i
ω
qν
ˆn
i
[u
i
(q,ν)d
qν
+ H.c.] (4.3)
H
e−e
=
1
2
i=j
V
c
(m − n) ˆn
i
ˆn
j
. (4.4)
Here
u
i
(q,ν) =
1
√
2N
γ(q,ν)e
iq·m
(4.5)
and
V
c
(m) =
1
N
q
V
c
(q)e
iq·m
(4.6)
are the matrix elements of the electron–phonon and Coulomb interactions,
respectively, in the Wannier representation for electrons, and ˆn
i
= c
†
i
c
i
is the
density operator. Assuming the interaction matrix elements depend only on the
momentum transfer, we neglect the terms in the electron–phonon and Coulomb
interactions which are proportional to the overlap integrals of the Wannier orbitals
on different sites. This approximation is justified for narrow-band materials,
Electron–phonon and Coulomb interactions
97
whose bandwidth 2D is less than the characteristic value of the crystal field. As a
result, in the Wannier representation, the Hamiltonian is
H =
i, j
[T (m − m
)δ
ss
− µδ
ij
]c
†
i
c
j
+
q,ν,i
ω
qν
ˆn
i
[u
i
(q,ν)d
qν
+ H.c.]
+
1
2
i=j
V
c
(m − n) ˆn
i
ˆn
j
+
q
ω
qν
(d
†
qν
d
qν
+ 1/2). (4.7)
This Hamiltonian should be treated as a ‘bare’ one for metals, where the matrix
elements and phonon frequencies are ill defined. In contrast, the bare phonons ω
qν
and the electron band structure E
nk
are well defined in doped semiconductors,
which have their ‘parent’ dielectric compounds. Here, the effect of carriers on the
crystal field and on the dynamic matrix is small while the carrier density is much
less than the atomic one. Therefore, we can use the band structure and the crystal
field of the parent insulators to calculate the parameters of the Hamiltonian (4.7).
Depending on the particular phonon branch, the interaction constant γ(q,ν) has
a different q-dependence. For example, in the long-wavelength limit (q π/a),
γ(q,ν)
1
q
constant
1
√
q
for optical, molecular (ω
q
constant) and acoustic (ω
q
q) phonons,
respectively. We can transform the e–ph interaction further using the site-
representation also for phonons. Replacing the Bloch functions in the definition
of γ(q,ν)(equation (3.20)) by their Wannier series yields
γ(q,ν) =−
1
M
1/2
ω
3/2
qν
n
e
−iq·n
e
qν
·∇
n
v(n). (4.8)
This result is obtained by neglecting the overlap integrals of the Wannier
orbitals on different sites and by assuming that the single-ion potential v(r)
varies over the distance, which is much larger than the radius of the orbital.
After substituting equation (4.8) into equation (4.5) and using the displacement
operators (equation (3.10)), one arrives at the following expression:
H
e−ph
=
m,n,s
ˆn
ms
u
n
·∇
n
v(m − n) (4.9)
which can also be derived by replacing the field operators by the Wannier series
in equation (3.8). The site representation of H
e−ph
(equation (4.9)) is particularly
convenient for the interaction with dispersionless local modes whose ω
qν
= ω
ν
and e
qν
= e
ν
are q independent. Introducing the phonon site operators
d
nν
=
1
√
N
k
e
iq·n
d
qν
(4.10)

98
Strong-coupling theory
we obtain in this case
u
n
=
ν
e
ν
√
2Mω
ν
(d
nν
+ d
†
nν
)
H
ph
=
n,ν
ω
ν
(d
†
nν
d
nν
+ 1/2)
and
H
e−ph
=
n,m,ν
ω
ν
g
ν
(m − n)(e
ν
· e
m−n
) ˆn
ms
(d
†
nν
+ d
nν
) (4.11)
where
g
ν
(m) =
1
ω
ν
√
2Mω
ν
dv(m)
dm
is a dimensionless force acting between the electron on site m and the
displacement of ion n,ande
m−n
≡ (m − n)/|m − n| is the unit vector in the
direction from the electron m to the ion n. The ‘real space’ representation (4.11)
is convenient in modelling the electron–phonon interaction in complex lattices.
Atomic orbitals of an ion adiabatically follow its motion. Therefore, the electron
does not interact with the displacement of the ion, whose orbital it occupies, that
is g
ν
(0) = 0.
4.2 Breakdown of Migdal–Eliashberg theory in the
strong-coupling regime
The perturbative approach to the e–ph interaction fails when λ>1. But one
might expect that the self-consistent Migdal–Eliashberg (ME) theory is still valid
in the strong-coupling regime because it sums the infinite set of particular (non-
crossing) diagrams in the electron self-energy (chapter 3). One of the problems
with such an extension of ME theory is lattice instability. The same theory applied
to phonons yields the renormalized phonon frequency ˜ω = ω(1 − 2λ)
1/2
[48].
The frequency turns out to be zero at λ = 0.5. Because of this lattice instability,
Migdal [48] and Eliashberg [36] restricted the applicability of their approach to
λ<1. However, it was then shown that there was no lattice instability but only a
small renormalization of the phonon frequencies of the order of the adiabatic ratio,
ω/µ 1, for any value of λ, if the adiabatic Born–Oppenheimer approach was
properly applied [77]. The conclusion was that the Fr¨ohlich Hamiltonian (4.3)
correctly describes the electron self-energy for any value of λ but it should not
be applied to further renormalize phonons (see also chapter 3). As a result, many
authors used ME theory with λ much larger than 1 [50].
In fact, the Migdal–Eliashberg theory cannot be applied at λ>1for
a reason, which has nothing to do with lattice instability. The inverse (1/λ)
expansion technique [11] showed that the many-electron system collapses into
a small polaron regime at λ ≈ 1 for any adiabatic ratio. This regime is beyond
Breakdown of Migdal–Eliashberg theory
99
ME theory. It cannot be described by a summation of the standard Feynman–
Dyson perturbation diagrams even including the vertex corrections (section 3.3),
because of the broken translation symmetry in the strong-coupling limit. The
major problem with the extension of ME theory to strong coupling originates from
its basic assumption that the electron and phonon GFs are translation invariants.
One assumes that G(r, r
,τ) = G(r − r
,τ) prior to solving the self-energy
equation. This assumption excludes the possibility of the breakdown of the
local translation symmetry due to lattice deformation, similar to the absence
of the anomalous Bogoliubov averages in any order of the perturbation theory
(section 3.4). To enable the electron relaxation into the lowest polaron states,
one has to introduce an infinitesimal translation-non-invariant potential in the
Hamiltonian which should be set equal to zero only in the final solution for the
GFs [78]. As in the case of the off-diagonal superconducting order parameter,
a small translation symmetry-breaking potential drives the system into a new
ground state, if the e–ph coupling is sufficiently strong (λ
1). Setting the
potential equal to zero in the solution of the equations of motion restores the
translation symmetry but in a new polaron band (section 4.3) rather than in the
bare electron band.
To illustrate the point let us compare the Migdal solution of the molecular-
chain (Holstein) model of the e–ph interaction [68] with the exact solution in the
adiabatic limit, ω/µ → 0. The Hamiltonian of the model is
H =−t
ij
c
†
i
c
j
+ H.c. +2(λkt)
1/2
i
x
i
c
†
i
c
i
+
i
−
1
2M
∂
2
∂x
2
i
+
kx
2
i
2
(4.12)
where t is the nearest-neighbour hopping integral, x
i
is the normal coordinate of
the molecule (site) i and k = Mω
2
. The Migdal theorem is exact in this limit.
Hence, in the framework of ME theory, one would expect Fermi-liquid behaviour
above T
c
and the BCS ground state below T
c
at any value of λ. In fact, the exact
ground state is a self-trapped insulator at any filling of the band if λ
1.
First, we consider a two-site case (zero-dimensional limit), i, j = 1, 2
with one electron and then generalize the result for an infinite lattice with many
electrons. The transformation X = (x
1
+ x
2
), ξ = x
1
− x
2
allows us to eliminate
the coordinate X , which is coupled only with the total density (n
1
+ n
2
= 1).
That leaves the following Hamiltonian to be solved in the extreme adiabatic limit
M →∞:
H =−t (c
†
1
c
2
+ c
†
2
c
1
) + (λkt)
1/2
ξ(c
†
1
c
1
− c
†
2
c
2
) +
kξ
2
4
. (4.13)
The solution is
ψ = (αc
†
1
+ βc
†
2
)|0 (4.14)

100
Strong-coupling theory
where
α =
t
[t
2
+ ((λkt)
1/2
ξ + (t
2
+ λktξ
2
)
1/2
)
2
]
1/2
(4.15)
β =−
(λkt)
1/2
ξ + (t
2
+ λktξ
2
)
1/2
[t
2
+ ((λkt)
1/2
ξ + (t
2
+ λktξ
2
)
1/2
)
2
]
1/2
(4.16)
and the energy is
E =
kξ
2
4
− (t
2
+ λktξ
2
)
1/2
. (4.17)
In the extreme adiabatic limit the displacement ξ is classical, so the ground-
state energy E
0
and the ground-state displacement ξ
0
are obtained by minimizing
equation (4.17) with respect to ξ.Ifλ ≥ 0.5, we obtain
E
0
=−t
λ +
1
4λ
(4.18)
and
ξ
0
=
t (4λ
2
− 1)
λk
1/2
. (4.19)
The symmetry-breaking ‘order’ parameter is
≡ β
2
− α
2
=
[2λ + (4λ
2
− 1)
1/2
]
2
− 1
[2λ + (4λ
2
− 1)
1/2
]
2
+ 1
. (4.20)
If λ<0.5, the ground state is translationally invariant, = 0andE
0
=−t,
ξ = 0,β =−α. Precisely this state is the ‘Migdal’ solution of the Holstein
model. Indeed, the Fourier transform of the GF should be diagonal in the Migdal
approximation, G(k, k
,τ) = G(k,τ)δ
k,k
. The site operators are transformed
into momentum space as
c
k
= N
−1/2
j
c
j
exp(ikaj) (4.21)
where k = 2πn/Na, −N/2 < n ≤ N/2. Then the off-diagonal GF with k = 0
and k
= π/a of the two-site chain (N = 2) is given by
G(k, k
, −0) =
i
2
(c
†
1
− c
†
2
)(c
1
+ c
2
) (4.22)
at τ =−0. Calculating this average, we obtain
G(k, k
, −0) =
i
2
(α
2
− β
2
) (4.23)
which should vanish in the Migdal theory. Hence, the theory provides only a
symmetric (translation invariant) solution with |α|=|β|.Whenλ>0.5, this

Breakdown of Migdal–Eliashberg theory
101
0.5 0.7 0.9 1.1 1.3
Λ
1.6
1.2
0.8
0.4
0.0
0.4
0.8
Et, order parameter
Figure 4.1. The ground-state energy (in units of t, full line) and the order parameter (thin
full line) of the adiabatic Holstein model. The Migdal solution is shown as the broken line.
solution is not the ground state of the system (figure 4.1). The system collapses
into a localized adiabatic polaron trapped on the ‘right-hand’ or ‘left-hand’ site
due to the finite lattice deformation ξ
0
. Alternatively, when λ<0.5, the Migdal
solution is the only solution.
The generalization to a multi-polaron system on an infinite lattice of any
dimension is straightforward in the extreme adiabatic regime. The adiabatic
solution of the infinite one-dimensional chain with one electron was obtained by
Rashba [79] in a continuous (i.e. effective mass) approximation and by Holstein
[68] and Kabanov and Mashtakov [80] for a discrete lattice. The latter authors
also studied the Holstein two-dimensional and three-dimensional lattices in the
adiabatic limit. According to [80], the self-trapping of a single electron occurs at
λ ≥ 0.875 and at λ ≥ 0.92 in two and three dimensions, respectively. The radius
of the self-trapped adiabatic polaron, r
p
, is readily derived from its continuous
wavefunction [79]
ψ(x) 1/ cosh(λx/a). (4.24)
It becomes smaller than the lattice constant (r
p
= a/λ)forλ ≥ 1. That
is why a multi-polaron system remains in a self-trapped insulating state in the
strong-coupling adiabatic regime, no matter how many polarons it has. The
only instability which might occur in this regime is the formation of on-site self-
trapped bipolarons (section 4.6), if the on-site attractive interaction, 2λzt,islarger
than the repulsive Hubbard U [14]. On-site self-trapped bipolarons form a charge-
ordered state due to a weak repulsion between them [10]. The asymptotically
exact many-particle ground state of the half-filled Holstein model in the strong-
coupling limit (λ →∞)is
ψ =
j ∈B
c
†
j ↑
c
†
j ↓
|0 (4.25)
for any value of the adiabatic ratio, ω/zt [10, 81]. Here the j sareB-sites of a
102
Strong-coupling theory
bipartite lattice A + B. It is an insulating state rather than a Fermi liquid, which
is expected in the Migdal approximation at any value of λ in the adiabatic limit,
ω → 0.
The non-adiabatic corrections (phonons) allow polarons and bipolarons to
propagate as Bloch states in a new narrow band (sections 4.3 and 4.6). Thus,
under certain conditions, the multi-polaron system is metallic with polaronic
or bipolaronic carriers rather than with bare electrons. There is a qualitative
difference between the ordinary Fermi liquid and the polaronic one. In particular,
the renormalized (effective) mass of electrons is independent of the ion mass M
in ordinary metals (equation (3.68)) because λ does not depend on the isotope
mass. In contrast, the polaron effective mass m
∗
will depend on M (section 4.3).
Hence, there is a large isotope effect on the carrier mass in polaronic metals [82]
(section 4.7.5) while there is no carrier mass isotope effect in ordinary metals.
Likewise, the bipolaron superconducting state is essentially different from the
BCS superconductor (section 4.5).
In the last years, quite a few numerical and analytical studies have confirmed
these conclusions (see, for example, [80–96]). In particular, Takada [86, 88]
applied the gauge-invariant self-consistent method neglecting the momentum
dependence of the vertex. Benedetti and Zeyher [91] applied the dynamical
mean-field theory in infinite dimensions. As in the 1/λ expansion technique,
both approaches avoided the problem of broken translation symmetry by using
the non-dispersive vertex and GFs as the starting point. As a result, they arrived
at the same conclusion about the applicability of the Migdal approach (in [91] the
critical value of λ was found to be 1.3 in the adiabatic limit).
The transition into the self-trapped state due to the broken translational
symmetry is expected at 0.5 <λ<1.3 (depending on the lattice dimensionality)
for any electron–phonon interaction conserving the on-site electron occupation
numbers. For example, Hiramoto and Toyozawa [97] calculated the strength of
the deformation potential, which transforms electrons into small polarons and
bipolarons. They found that the transition of two electrons into a self-trapped
small bipolaron occurs at the electron–acoustic phonon coupling λ 0.5, that is
half of the critical value of λ at which the transition of the electron into the small
acoustic polaron takes place in the extreme adiabatic limit, sq
D
zt. The effect
of the adiabatic ratio sq
D
/zt on the critical value of λ was found to be negligible.
The radius of the acoustic polaron and bipolaron is about the lattice constant, so
that the critical value of λ does not very much depend on the number of electrons
in this case either.
4.3 Polaron dynamics
4.3.1 Polaron band
The kinetic energy is smaller than the interaction energy as long as λ>1. Hence,
a self-consistent approach to the many-polaron problem is possible with the ‘1/λ’
Polaron dynamics
103
expansion technique [98], which treats the kinetic energy as a perturbation. The
technique is based on the fact, known for a long time, that there is an analytical
exact solution of a single polaron problem in the strong-coupling limit λ →∞
[71]. Following Lang and Firsov, we apply the canonical transformation e
S
to
diagonalize the Hamiltonian. The diagonalization is exact if T (m) = 0(or
λ =∞):
˜
H = e
S
H e
−S
(4.26)
where
S =−
q,ν,i
ˆn
i
[u
i
(q,ν)d
qν
− H.c.] (4.27)
is such that S
†
=−S. The electron and phonon operators are transformed as
˜c
i
= c
i
exp
q,ν
u
i
(q,ν)d
qν
− H.c.
(4.28)
and
˜
d
qν
= d
qν
−
i
ˆn
i
u
∗
i
(q,ν) (4.29)
respectively (appendix E). It follows from equation (4.29) that the Lang–Firsov
canonical transformation shifts the ions to new equilibrium positions. In a
more general sense, it changes the boson vacuum. As a result, the transformed
Hamiltonian takes the following form:
˜
H =
i, j
[ˆσ
ij
−µδ
ij
]c
†
i
c
j
− E
p
i
ˆn
i
+
q,ν
ω
qν
(d
†
qν
d
qν
+1/2) +
1
2
i=j
v
ij
ˆn
i
ˆn
j
(4.30)
where
ˆσ
ij
= T (m − n)δ
ss
exp
q,ν
[u
j
(q,ν)− u
i
(q,ν)]d
qν
− H.c.
(4.31)
is the renormalized hopping integral depending on the phonon operators and
v
ij
≡ v(m − n)
= V
c
(m − n) −
1
N
q,ν
|γ(q,ν)|
2
ω
qν
cos[q · (m − n)] (4.32)
is the interaction of polarons comprising their Coulomb repulsion and the
interaction via a local lattice deformation. In the extreme infinite-coupling limit
(λ →∞) we can neglect the hopping term of the transformed Hamiltonian. The
rest has analytically determined eigenstates and eigenvalues. The eigenstates
|
˜
N=|n
i
, n
qν
are sorted by the polaron n
ms
and phonon n
qν
occupation
numbers. The energy levels are
E =−(µ + E
p
)
i
n
i
+
1
2
i=j
v
ij
n
i
n
j
+
q
ω
qν
(n
qν
+ 1/2) (4.33)
104
Strong-coupling theory
where n
i
= 0, 1andn
qν
= 0, 1, 2, 3,...,∞.
The Hamiltonian (4.30), in zero order with respect to the hopping describes
localized polarons and independent phonons, which are vibrations of ions relative
to new equilibrium positions, which depend on the polaron occupation numbers.
The phonon frequencies remain unchanged in this limit. The middle of the
electron band falls by the polaron level-shift E
p
due to a potential well created by
lattice deformation,
E
p
=
1
2N
q,ν
|γ(q,ν)|
2
ω
qν
. (4.34)
Now let us discuss the 1/λ expansion. First we restrict the discussion to
a single-polaron problem with no polaron–polaron interaction and µ = 0. The
finite hopping term leads to the polaron tunnelling because of degeneracy of the
zero-order Hamiltonian with respect to the site position of the polaron. To see
how the tunnelling occurs, we apply the perturbation theory using 1/λ as a small
parameter, where
λ ≡
E
p
D
. (4.35)
Here D = zT(a), z is the coordination lattice number and T (a) is the nearest-
neighbour hopping integral. The proper Bloch set of N-degenerate zero-order
eigenstates with the lowest energy (−E
p
) of the unperturbed Hamiltonian is
|k , 0=
1
√
N
m
c
†
ms
exp(ik · m)|0 (4.36)
where |0 is the vacuum. By applying the textbook perturbation theory, one
readily calculates the perturbed energy levels. Up to the second order in the
hopping integral, they are given by
E(k) =−E
p
+
k
−
k
,n
qν
|k , 0|
i, j
ˆσ
ij
c
†
i
c
j
|k
, n
qν
|
2
q,ν
ω
qν
n
qν
(4.37)
where |k
, n
qν
are the excited states of the unperturbed Hamiltonian with one
electron and at least one real phonon. The second term in equation (4.37), which is
linear with respect to the bare hopping T (m), describes a polaron-band dispersion,
k
=
m
T (m)e
−g
2
(m)
exp(−ik · m) (4.38)
where
g
2
(m) =
1
2N
q,ν
|γ(q,ν)|
2
[1 −cos(q · m)] (4.39)
is the band-narrowing factor at zero temperature. The third term in
equation (4.37), quadratic in T (m), yields a negative k-independent correction
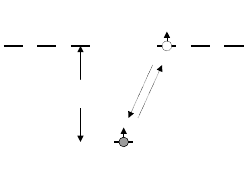
Polaron dynamics
105
(
S
P
Q
Figure 4.2. ‘Back and forth’ virtual transitions of the polaron without any transfer of the
lattice deformation from one site to another. These transitions shift the middle of the band
down without any real charge delocalization.
to the polaron level-shift of the order of 1/λ
2
. The origin of this correction,
which could be much larger than the first-order contribution (equation (4.38))
(containing a small exponent), is understood in figure 4.2. The polaron localized
in the potential well of depth E
p
on site m hops onto a neighbouring site n with
no deformation around and comes back. As in any second-order correction, this
transition shifts the energy down by an amount of about −T
2
(m)/E
p
. It has little
to do with the polaron effective mass and the polaron tunnelling mobility because
the lattice deformation around m does not follow the electron. The electron hops
back and forth many times (about e
g
2
) waiting for a sufficient lattice deformation
to appear around the site n. Only after the deformation around n is created does
the polaron tunnel onto the next site together with the deformation.
4.3.2 Damping of the polaron band
The polaron band is exponentially narrow, see equation (4.38). Hence, one
can raise a concern about its existence in real solids. At zero temperature
the perturbation term of the transformed Hamiltonian conserves the momentum
because all off-diagonal matrix elements vanish:
k, 0|
i, j
ˆσ
i, j
c
†
i
c
j
|k
, 0=0 (4.40)
if k = k
. The emission of a single high-frequency phonon is impossible for any k
because of the energy conservation. The polaron half-bandwidth is exponentially
reduced,
w ≈ De
−g
2
(4.41)
and it is usually less than the optical phonon energy ω
0
(g
2
is of the order of
Dλ/ω
0
). Hence, there is no damping of the polaron band at T = 0 caused by
optical phonons, no matter how strong the interaction is. These phonons ‘dress’
the electron and coherently follow its motion. However, at finite temperatures, the
simultaneous emission and absorption of phonons (figure 4.3) become possible.
