Alexandrov A.S.,Theory of Superconductivity - From Weak to Strong Coupling
Подождите немного. Документ загружается.

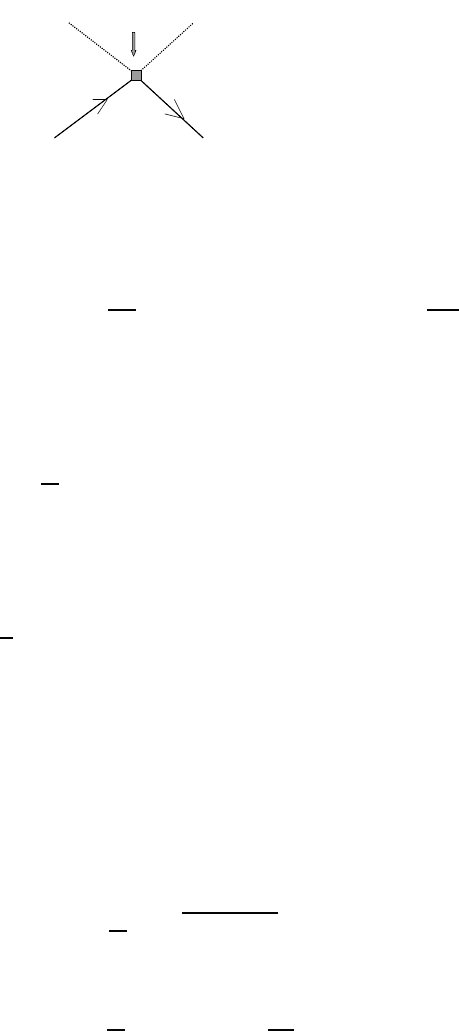
106
Strong-coupling theory
TTC
N
NTTC
∼γ
Z
Figure 4.3. Two-phonon scattering responsible for the damping of the polaron band.
Moreover, the polaron bandwidth shrinks with increasing temperature because the
phonon-averaged hopping integrals depend on temperature (appendix E):
ˆσ
ij
ph
= T (m − n)δ
ss
exp
−
1
2N
q,ν
|γ(q,ν)|
2
[1 −cos(q · m)]coth
ω
qν
2T
.
For high temperatures (T ω
0
/2) the band narrows exponentially:
w ≈ De
−T / T
0
(4.42)
where
T
−1
0
=
1
N
q,ν
|γ(q,ν)|
2
ω
−1
qν
[1 −cos(q · m)].
However, the two-phonon scattering of polarons (figure 4.3) becomes more
important with increasing temperature.
We can estimate the scattering rate by applying the Fermi–Dirac golden rule:
1
τ
= 2π
q,q
|M
qq
|
2
δ(
k
−
k+q−q
)
!
ph
(4.43)
where the corresponding matrix element is
M
qq
=
i, j
k + q − q
, n
q
− 1, n
q
+ 1|ˆσ
i, j
c
†
i
c
j
|k , n
q
, n
q
.
For simplicity we drop the phonon branch index ν and consider the momentum
independent γ(q) = γ
0
and ω
q
= ω
0
. Expanding ˆσ
ij
-operators in powers of the
phonon creation and annihilation operators, we estimate the matrix element of the
two-phonon scattering as
M
qq
≈
1
N
wγ
2
0
n
q
(n
q
+ 1). (4.44)
Using this estimate and the polaron density of states,
N
p
(ξ) ≡
1
N
k
δ(ξ −
k
) ≈
1
2w
(4.45)
Polaron dynamics
107
we obtain
1
τ
≈ wγ
4
0
n
ω
(1 + n
ω
) (4.46)
where n
ω
=[exp(ω
0
/T ) −1]
−1
is the phonon distribution function. The polaron
band is well defined if
1
τ
<w (4.47)
which is satisfied for a wide temperature range
T ≤ T
min
≈
ω
0
ln γ
4
0
(4.48)
about half of the characteristic phonon frequency for relevant values of γ
2
0
.
Phonons dominate in the scattering at finite temperatures if the number of
impurities is sufficiently low. Therefore, the polaron mobility decreases when the
temperature increases from zero to T
min
due to an increasing number of phonons.
At higher temperatures, the incoherent thermal activated hopping dominates in
the polaron dynamics [66–68, 71] and the polaron states are no longer the Bloch
states. Hence, the mobility increases above T
min
, where it is at minimum, due
to thermal activated hopping. There is a temperature range around T
min
where
the thermal activated hopping still makes a small contribution to the conductivity
but the uncertainty in the polaron band is already significant [71]. The polaron
transport theory requires a special diagrammatic technique in this region [74,75].
The optical phonon frequencies are exceptionally high, about 1000 K or even
higher and polarons are in Bloch states in the whole relevant range of temperatures
in novel superconductors.
4.3.3 Small Holstein polaron and small Fr
¨
ohlich polaron
The narrowing of the band and the polaron effective mass strongly depend on
the radius of the electron–phonon interaction [100]. Let us compare the small
Holstein polaron (SHP) formed by the short-range e–ph interaction and a small
polaron formed by the long-range (Fr¨ohlich) interaction, which we refer as the
small Fr¨ohlich polaron (SFP). Introducing a normal coordinate at site n as
ξ
n
=
q
(2NMω
q
)
−1/2
e
iq·n
d
q
+ H.c. (4.49)
and a ‘force’ between the electron at site m and the normal coordinate ξ
n
,
f (m) = N
−1
q
γ(q)(Mω
3
q
)
1/2
e
iq·m
(4.50)
we rewrite the e–ph interaction, equation (4.3), as
H
e−ph
=
n,i
f (m − n)ξ
n
ˆn
i
. (4.51)

108
Strong-coupling theory
For simplicity we consider the interaction with a single phonon branch and
γ(−q) = γ(q). In general, there is no simple relation between the polaron level
shift E
p
and the exponent g
2
of the mass enhancement. This relation depends on
the form of the electron–phonon interaction. Indeed, for dispersionless phonons,
ω
q
= ω
0
, using equations (4.34) and (4.39) we obtain
E
p
=
1
2Mω
2
0
m
f
2
(m) (4.52)
and
g
2
=
1
2Mω
3
0
m
[f
2
(m) − f (m) f (m + a)] (4.53)
where a is the primitive lattice vector. In the nearest-neighbour approximation,
the effective mass renormalization is given by
m
∗
/m = e
g
2
where m is the bare band mass and 1/m
∗
= ∂
2
k
/∂k
2
at k → 0istheinverse
polaron mass.
If the interaction is short range, f (m) = κδ
m,0
(the Holstein model), then
g
2
= E
p
/ω.Hereκ is a constant. In general, we have g
2
= γ E
p
/ω with the
numerical coefficient
γ =
1 −
m
f (m) f (m + a)
n
f
2
(n)
(4.54)
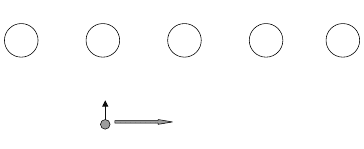
which might be less than 1. To estimate γ , let us consider a one-dimensional chain
model with a long-range Coulomb interaction between the electron on the chain
(×) and ion vibrations of the chain (◦), polarized in a direction perpendicular to
the chains [94] (figure 4.4). The corresponding force is given by
f (m − n) =
κ
(|m − n|
2
+ 1)
3/2
. (4.55)
Here the distance along the chains, |m − n|, is measured in units of the lattice
constant, a, the inter-chain distance is also a and we take a = 1. For this long-
range interaction, we obtain E
p
= 1.27κ
2
/(2Mω
2
), g
2
= 0.49κ
2
/(2Mω
3
) and
g
2
= 0.39E
p
/ω. (4.56)
Thus the effective mass renormalization is much smaller than in the Holstein
model, roughly m
∗
SFP
∝ (m
∗
SHP
)
1/2
.
Not only does the small polaron mass strongly depend on the radius of the
electron–phonon interaction but the range of the applicability of the analytical
1/λ expansion theory also does. The theory appears almost exact in a wide
region of parameters for the Fr¨ohlich interaction. The exact polaron mass in a
Polaron dynamics
109
7D
2
3
;;;;;
Figure 4.4. A one-dimensional model of a small polaron on the chain interacting with the
ion displacements of another chain.
wide region of the adiabatic parameter ω/T (a) and coupling was calculated with
the continuous-time path-integral quantum Monte Carlo (QMC) algorithm [94].
This method is free from any systematic finite-size, finite-time-step and finite-
temperature errors and allows for an exact (in the QMC sense) calculation of the
ground-state energy and the effective mass of the lattice polaron for any electron–
phonon interaction described by the Hamiltonian (4.51).
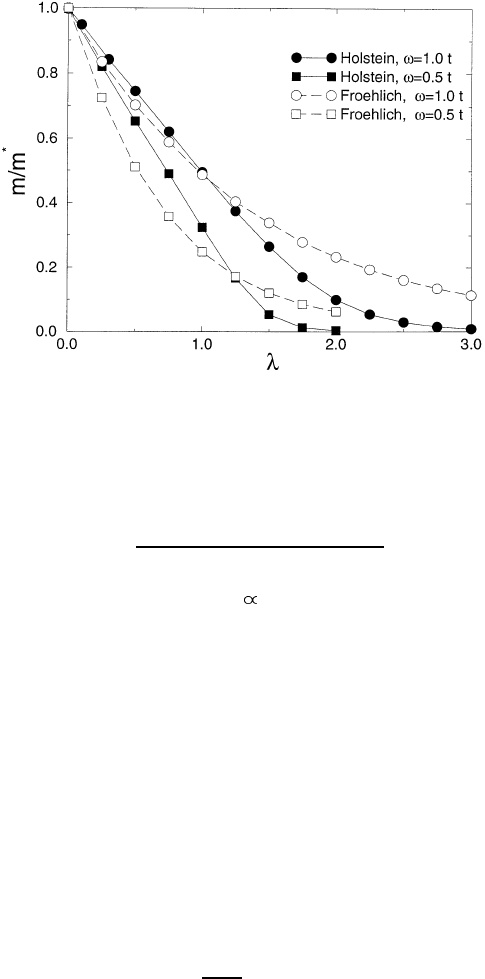
At large λ (>1.5), the SFP was found to be much lighter than the SHP, while
the large Fr¨ohlich polaron (i.e. at λ<1) was heavier than the large Holstein
polaron with the same binding energy (figure 4.5). The mass ratio m
∗
FP
/m
∗
HP
is
a non-monotonic function of λ. The effective mass of Fr
¨
ohlich polarons, m
∗
FP
(λ)
is well fitted by a single exponent, which is e
0.73λ
for ω
0
= T (a) and e
1.4λ
for
ω = 0.5T (a). The exponents are remarkably close to those obtained with the
Lang–Firsov transformation, e
0.78λ
and e
1.56λ
, respectively. Hence, in the case
of the Fr¨ohlich interaction the transformation is perfectly accurate even in the
moderate adiabatic regime, ω/T (a) ≤ 1forany coupling strength. This is not the
case for the Holstein polaron. If the interaction is short range, the same analytical
technique is applied only in the non-adiabatic regime ω/T (a)>1.
Another interesting point is that the size of the SFP and the length over which
the distortion spreads are different. In the strong-coupling limit, the polaron is
almost localized on one site m. Hence, the size of its wavefunction is the atomic
size. In contrast, the ion displacements, proportional to the displacement force
f (m − n), spread over a large distance. Their amplitude at a site n falls with
distance as |m − n|
−3
in our one-dimensional model. The polaron cloud (i.e.
lattice distortion) is more extended than the polaron itself [66, 72, 100]. Such a
polaron tunnels with a larger probability than the Holstein polaron due to a smaller
relative lattice distortion around two neighbouring sites. For a short-range e–ph
interaction, the entire lattice deformation disappears at one site and then forms at
its neighbour, when the polaron tunnels from site to site. Therefore, γ = 1and
the polaron is very heavy already at λ ≈ 1. In contrast, if the interaction is long-
ranged, only a fraction of the total deformation changes every time the polaron
tunnels from one site to its neighbour and γ is smaller than 1. The fact that the
Lang–Firsov transformation is rather accurate for the long-range interaction in
a wide region of parameters, allows us to generalize this result. Including all
110
Strong-coupling theory
Figure 4.5. Inverse effective polaron mass in units of 1/m = 2T (a)a
2
.
phonon branches in the three-dimensional lattice, we obtain m
∗
SFP
= (m
∗
SHP
)
γ
,
where the masses are measured in units of the band mass, and
γ =
q,ν
γ
2
(q,ν)[1 − cos(q · m)]
q,ν
γ
2
(q,ν)
. (4.57)
For the Fr¨ohlich interaction (i.e. γ(q)
1/q), we find γ = 0.57 in a cubic
lattice and γ = 0.255 for the in-plane oxygen hole in cuprates (Part II). A lighter
mass of SFP compared with the non-dispersive SHP is a generic feature of any
dispersive electron–phonon interaction. As an example, a short-range interaction
with dispersive acoustic phonons (γ(q) ∼ 1/q
1/2
, ω
q
∼ q) also leads to a lighter
polaron in the strong-coupling regime compared with the SHP. Actually, Holstein
[68] pointed out in his original paper that the dispersion is a vital ingredient of the
polaron theory.
4.3.4 Polaron spectral and Green’s functions
The multi-polaron problem has an exact solution in the extreme infinite-coupling
limit (λ =∞) for any type of e–ph interaction conserving the on-site occupation
numbers of electrons (equation (4.3)). For finite coupling, the 1/λ perturbation
expansion is applied. The expansion parameter is actually [72, 74,98, 99]
1
2zλ
2
1
so that the analytical perturbation theory has a wider region of applicability
than one can expect using a semiclassical estimate E
p
> D.However,

Polaron dynamics
111
the expansion convergency is different for different e–ph interactions. Exact
numerical diagonalizations of vibrating clusters, variational calculations [83, 85,
87, 89, 92, 93], dynamical mean-field approach in infinite dimensions [91], and
quantum Monte Carlo simulations [94] revealed that the ground state energy
(≈−E
p
) is not very sensitive to the parameters. In contrast, the effective mass, the
bandwidth and the polaron density of states strongly depend on the adiabatic ratio
ω/T (a) and on the radius of the interaction. The first order in 1/λ perturbation
theory is practically exact in the non-adiabatic regime (ω/T (a)>1) for any
value of the coupling constant and any type of e–ph interaction. However, it
overestimates the polaron mass by a few orders of magnitude in the adiabatic
case (ω/T (a)<1), if the interaction is short-ranged [83]. A much lower
effective mass of the adiabatic Holstein polaron compared with that estimated
using first-order perturbation theory is the result of the poor convergency of the
perturbation expansion owing to the double-well potential [68] in the adiabatic
limit. The tunnelling probability is extremely sensitive to the shape of this
potential. However, the analytical theory is practically exact in a wider range of
the adiabatic parameter and of the coupling constant for the long-range Fr¨ohlich
interaction.
Keeping this in mind, let us calculate the one-particle GF in the first
order in 1/λ. Applying the canonical transformation we write the transformed
Hamiltonian as
˜
H = H
p
+ H
ph
+ H
int
(4.58)
where
H
p
=
k
ξ(k)c
†
k
c
k
(4.59)
is the ‘free’ polaron contribution and
H
ph
=
q
ω
q
(d
†
q
d
q
+ 1/2) (4.60)
is the free phonon part. For simplicity, we drop the spin and phonon branch
indexes. Here ξ(k) = Z
E(k) − µ is the renormalized polaron band dispersion.
The chemical potential µ includes the polaron level shift −E
p
. It might also
include all higher orders in 1/λ corrections to the spectrum independent of k.
E(k) =
m
T (m) exp(−ik · m) is the bare dispersion in the rigid lattice and
Z
=
m
T (m)e
−g
2
(m)
exp(−ik · m)
m
T (m) exp(−ik · m)
(4.61)
is the band-narrowing factor (Z
= exp(−γ E
p
/ω)) as discussed earlier). The
interaction term H
int
comprises the polaron–polaron interaction, equation (4.32),
and the residual polaron–phonon interaction
H
p−ph
≡
i=j
[ˆσ
ij
−ˆσ
ij
ph
]c
†
i
c
j
. (4.62)

112
Strong-coupling theory
We can neglect H
p−ph
in the first order in 1/λ 1. To better understand the
spectral properties of a single polaron, let us also neglect the polaron–polaron
interaction. If H
int
= 0, the energy levels are
E
{˜m}
=
k
ξ
k
n
k
+
q
ω
q
[n
q
+ 1/2] (4.63)
and the transformed eigenstates |˜m are sorted by the polaron Bloch-state
occupation numbers, n
k
= 0, 1, and the phonon occupation numbers, n
q
=
0, 1, 2,...,∞. The spectral function (equation (D.10)) is defined by the matrix
element n|c
k
|m. It can be written as
n|c
k
|m=
1
√
N
m
e
−ik·m
˜n|c
i
ˆ
X
i
|˜m (4.64)
by the use of the Wannier representation and the Lang–Firsov transformation.
Here
ˆ
X
i
= exp
q
u
i
(q)d
q
− H.c.
.
Now, applying the Fourier transform of the δ-function in equation (D.10),
δ(ω
nm
+ ω) =
1
2π
∞
−∞
dt e
i(ω
nm
+ω)t
the spectral function is expressed as
A(k,ω) =
1
2
∞
−∞
dt e
iωt
1
N
m,n
e
ik·(n−m)
×{c
i
(t)
ˆ
X
i
(t)c
†
j
ˆ
X
†
j
+ c
†
j
ˆ
X
†
j
c
i
(t)
ˆ
X
i
(t)}. (4.65)
Here the quantum and statistical averages are performed for independent polarons
and phonons, therefore
c
i
(t)
ˆ
X
i
(t)
ˆ
X
†
j
c
†
i
= c
i
(t)c
†
j
ˆ
X
i
(t)
ˆ
X
†
j
. (4.66)
The Heisenberg free-polaron operator evolves with time as
c
k
(t) = c
k
e
−iξ
k
t
(4.67)
and
c
i
(t)c
†
i
=
1
N
k
,k
e
i(k
·m−k
·n)
c
k
(t)c
†
k
=
1
N
k
[1 −¯n(k
)]e
ik
·(m−n)−iξ
k
t
(4.68)
c
†
i
c
i
(t) =
1
N
k
¯n(k
)e
ik
·(m−n)−iξ
k
t
(4.69)

Polaron dynamics
113
where ¯n(k) =[1 + exp ξ
k
/T ]
−1
is the Fermi–Dirac distribution function of
polarons. The Heisenberg free-phonon operator evolves in a similar way,
d
q
(t) = d
q
e
−iω
q
t
and
ˆ
X
i
(t)
ˆ
X
†
j
=
q
exp[u
i
(q, t)d
q
− H.c.]exp[−u
j
(q)d
q
− H.c.] (4.70)
where u
i, j
(q, t) = u
i, j
(q)e
−iω
q
t
. This average is calculated using the operator
identity (appendix E)
e
ˆ
A+
ˆ
B
= e
ˆ
A
e
ˆ
B
e
−[
ˆ
A,
ˆ
B]/2
(4.71)
which is applied for any two operators
ˆ
A and
ˆ
B, whose commutator [
ˆ
A,
ˆ
B] is a
number. Because [d
q
, d
†
q
]=1, we can apply this identity in equation (4.70) to
obtain
e
[u
i
(q,t)d
q
−H.c.]
e
[−u
j
(q)d
q
−H.c.]
= e
(α
∗
d
†
q
−αd
q
)
× e
[u
i
(q,t)u
∗
j
(q)−u
∗
i
(q,t)u
j
(q)]/2
where α ≡ u
j
(q, t) − u
i
(q). Applying once again the same identity yields
e
[u
i
(q,t)d
q
−H.c.]
e
[−u
j
(q)d
q
−H.c.]
= e
α
∗
d
†
q
e
−αd
q
e
−|α|
2
/2
× e
[u
i
(q,t)u
∗
j
(q)−u
∗
i
(q,t)u
j
(q)]/2
. (4.72)
Now the quantum and statistical averages are calculated by the use of
(appendix E)
e
α
∗
d
†
q
e
−αd
q
= e
−|α|
2
n
ω
(4.73)
where n
ω
=[exp(ω
q
/T ) − 1]
−1
is the Bose–Einstein distribution function of
phonons. Collecting all multiplies in equation (4.72), we arrive at
ˆ
X
i
(t)
ˆ
X
†
j
= exp
−
1
2N
q
|γ(q)|
2
f
q
(m − n, t)
(4.74)
where
f
q
(m, t) =[1 −cos(q · m) cos(ω
q
t)]coth
ω
q
2T
+ i cos(q · m) sin(ω
q
t). (4.75)
Here we have used the symmetry of γ(−q) = γ(q), and, hence, the terms
containing sin(q · m) have disappeared. The average
ˆ
X
†
j
ˆ
X
i
(t), which is a
multiplier in the second term in the brackets of equation (4.65), is obtained by
replacing u
i
(q, t) u
j
(q) in the previous expressions. The result is
ˆ
X
†
j
ˆ
X
i
(t) =
ˆ
X
i
(t)
ˆ
X
†
j
∗
. (4.76)
114
Strong-coupling theory
To proceed with the analytical results, we consider low temperatures, T ω
q
,
when coth(ω
q
/2T ) ≈ 1. Then expanding the exponent in equation (4.74) yields
ˆ
X
i
(t)
ˆ
X
†
j
= Z
∞
l=0
{
q
|γ(q)|
2
e
i[q·(m−n)−ω
q
t]
}
l
(2N)
l
l!
(4.77)
where
Z = exp
−
1
2N
q
|γ(q)|
2
. (4.78)
Substituting equations (4.77) and (4.68) into equation (4.66) and performing
summation with respect to m, n, k
and integration with respect to time in
equation (4.65), we arrive at [101]
A(k,ω) =
∞
l=0
[A
(−)
l
(k,ω)+ A
(+)
l
(k,ω)] (4.79)
where
A
(−)
l
(k,ω) = π Z
q
1
,...,q
l
"
l
r=1
|γ(q
r
)|
2
(2N)
l
l!
×
1 −¯n
k −
l
r=1
q
r
δ
ω−
l
r=1
ω
q
r
−ξ
k−
l
r=1
q
r
(4.80)
and
A
(+)
l
(k,ω) = π Z
q
1
,...,q
l
"
l
r=1
|γ(q
r
)|
2
(2N)
l
l!
ׯn
k +
l
r=1
q
r
δ
ω+
l
r=1
ω
q
r
−ξ
k+
l
r=1
q
r
. (4.81)
Obviously, equation (4.79) is in the form of a perturbative multi-phonon
expansion. Each contribution A
(±)
l
(k,ω) to the spectral function describes the
transition from the initial state k of the polaron band to the final state k±
l
r=1
q
r
with the emission (or absorption) of l phonons. The 1/λ expansion result
(equation (4.79)) is applied to low-energy polaron excitations in the strong-
coupling limit. In the case of the long-range Fr¨ohlich interaction with high-
frequency phonons, it is also applied in the weak-coupling and intermediate
regimes (section 4.3.3). Differing from the canonical Migdal GF (chapter 3),
there is no damping of polaronic excitations in equation (4.79). Instead the e–ph
coupling leads to the coherent dressing of electrons by phonons because of the

Polaron dynamics
115
energy conservation (section 4.3.2). The dressing can be seen as the phonon ‘side-
bands’ with l ≥ 1. While the major sum rule (equation (D.11)) is satisfied,
1
π
∞
−∞
dω A(k,ω) = Z
∞
l=0
q
1
,...,q
l
"
l
r=1
|γ(q
r
)|
2
(2N)
l
l!
= Z
∞
l=0
1
l!
1
2N
q
|γ(q)|
2
l
= Z exp
1
2N
q
|γ(q)|
2
= 1 (4.82)
the higher-momentum integrals,
∞
−∞
dωω
p
A(k,ω)with p > 0, calculated using
equation (4.79), differ from the exact value by an amount proportional to 1/λ.
The difference is due to a partial ‘undressing’ of high-energy excitations in the
side-bands, which is beyond the first-order 1/λ expansion.
The spectral function of the polaronic carriers comprises two different parts.
The first (l = 0) k-dependent coherent term arises from the polaron band
tunnelling,
A
coh
(k,ω) =[A
(−)
0
(k,ω)+ A
(+)
0
(k,ω)]=π Z δ(ω − ξ
k
). (4.83)
The spectral weight of the coherent part is suppressed as Z 1. However,
in the case of the Fr¨ohlich interaction, the effective mass is less enhanced,
ξ
k
= Z
E
k
− µ, because Z Z
< 1 (section 4.3.3). The second incoherent
part A
incoh
(k,ω) comprises all the terms with l ≥ 1. It describes the excitations
accompanied by emission and absorption of phonons. We note that its spectral
density spreads over a wide energy range of about twice the polaron level shift
E
p
, which might be larger than the unrenormalized bandwidth 2D in the rigid
lattice without phonons. In contrast, the coherent part shows a dispersion only
in the energy window of the order of the polaron bandwidth, 2w = 2Z
D.It
is interesting that there is some k dependence of the incoherent background as
well, if the matrix element of the e–ph interaction and/or phonon frequencies
depend on q. Only in the Holstein model with the short-range dispersionless
e–ph interaction (γ(q) = γ
0
and ω
q
= ω
0
) is the incoherent part momentum
independent. Replacing k ±
l
r=1
q
r
by k
in equations (4.80) and (4.81), we
obtain the following expression in this case:
A
incoh
(k,ω) = π
Z
N
∞
l=1
γ
2l
0
2
l
l!
×
k
{[1 −¯n(k
)]δ(ω − lω
0
− ξ
k
) +¯n(k
)δ(ω +lω
0
− ξ
k
)}
(4.84)
