Alexandrov A.S.,Theory of Superconductivity - From Weak to Strong Coupling
Подождите немного. Документ загружается.


226
Superconducting state of cuprates
Figure 8.8. Theoretical conductance of figure 8.7 for g
2
= 0.5625 (full line) compared
with the tunnelling spectrum obtained on Bi
2
Sr
2
CaCu
2
O
8+δ
single crystals by the
break-junction technique [268] (dots).
main peaks in the superconducting state of an SIS junction, while the incoherent
temperature-independent part
p
survives well above T
c
as observed [274, 275].
8.4 ARPES
Let us discuss ARPES in doped charge-transfer Mott insulators in the framework
of bipolaron theory [262] to describe some unusual ARPES features of high-T
c
YBa
2
Cu
3
O
7−δ
(Y123), YBa
2
Cu
4
O
8
(Y124) and several other materials.
Perhaps the most intriguing feature of ARPES in cuprates is an extremely
narrow and intense peak lying below the Fermi energy, which is most clearly
seen near the Y and X points in Y124 [278], and Y123 [279]. Its angular
dependence and spectral shape as well as the origin of the featureless (but
dispersive) background remain unclear. Some authors [278] refer to the peak
as an extended van Hove singularity (evHs) arising from a plane (CuO
2
) strongly
correlated band. They also implicate the resulting (quasi-)one-dimensional DOS
singularity as a possible origin for the high transition temperature. However,
polarized ARPES studies of untwinned Y123 crystals of exceptional quality [279]
unambiguously show that the peak is a narrow resonance arising primarily from
the quasi-one-dimensional CuO
3
chains in the buffer layers rather than from the
planes. Interestingly, a very similar narrow peak was observed by Park et al [280]
in high-resolution ARPES near the gap edge of the cubic semiconductor FeSi with
no Fermi surface at all.
As discussed in section 5.2, cuprates and many other transition metal
compounds are charge transfer Mott–Hubbard insulators, where the first band to
be doped is the oxygen band lying within the Hubbard gap, as shown in figure 5.3.

ARPES
227
A single photoexited oxygen hole is described by the polaron spectral function of
section 4.3.4. Its low-energy part is affected by low-frequency thermal lattice,
spin and random fluctuations. The latter can be described as a ‘Gaussian white
noise’ potential. Also p-hole polarons in oxides are almost one-dimensional due
to a large difference in the ppσ and ppπ hopping integrals. This allows us
to explain the shape of the narrow peaks in ARPES using the spectral density
A(k, E) of a one-dimensional particle in a Gaussian white noise potential [281].
8.4.1 Photocurrent
The interaction of the crystal with the electromagnetic field of frequency ν is
described by the following Hamiltonian (in the dipole approximation):
H
int
= (8π I )
1/2
sin(νt)
k,k
(e · d
kk
)c
†
k
h
†
k
+ H.c. (8.40)
where I is the intensity of the radiation with polarization e, k is the momentum
of the final state (i.e. of the photoelectron registered by the detector), k
is the
(quasi-)momentum of the hole remaining in the sample after the emission and
c
†
k
and h
†
k
are their creation operators, respectively. For simplicity, we suppress
the band index in h
†
k
. Due to the translational symmetry of the Bloch states,
|k
≡u
−k
(r) exp(−ik
· r) (appendix A), there is a momentum conservation in
the dipole matrix element,
d
kk
= d(k)δ
k+k
,G
(8.41)
with
d(k) = ie(N/v
0
)
1/2
∇
k
v
0
e
−iG·r
u
k−G
(r) dr (8.42)
and v
0
is the unit cell volume (G is a reciprocal-lattice vector). The Fermi–Dirac
golden rule gives the photocurrent to be
I (k, E) = 4π
2
I |e·d(k)|
2
i, f
e
+µN
i
−E
i
|f |h
†
k−G
|i f |
2
δ(E +E
f
−E
i
) (8.43)
where E is the binding energy, E
i, f
is the energy of the initial and final states and
,µ, N
i
are the thermodynamic and chemical potentials and number of holes,
respectively. By definition, the sum in equation (8.43) is n(E)A(k − G, −E),
where the spectral function
A(k − G, E) =−
1
π
Im G
R
(k − G, E) (8.44)
is proportional to the imaginary part of the retarded GF (appendix D) and
n(E) =[exp(E/ T )+1]
−1
is the Fermi distribution. In the following, we consider

228
Superconducting state of cuprates
temperatures well below the experimental energy resolution, so that n(E) = 1, if
E is negative, and zero otherwise, and we put G = 0.
The spectral function depends on essential interactions of a single hole
with the rest of the system. The most important interaction in oxides is
the Fr¨ohlich electron–phonon interaction with c-axis polarized high-frequency
phonons (section 5.2), which leads to the polaron spectral function (4.79). As a
result, we obtain
I (k, E) ∼|d(k)|
2
n(E)Z δ(E + ξ
k
) + I
incoh
(k, E) (8.45)
where I
incoh
(k, E) is an incoherent part, which spreads from about −ω
0
down to
−2E
p
. There might be some multi-phonon structure in I
incoh
(k, E) as observed
in tunnelling (section 8.3).
Here we concentrate on the angular, spectral and polarization dependence of
the first coherent term in equation (8.45). The present experimental resolution
[264] allows the intrinsic damping of the coherent quasi-particle excitations to be
probed. The damping appears due to a random field and low-frequency lattice
and spin fluctuations described by the polaron self-energy, (k, E), so that the
coherent part of the spectral function is given by
A
c
(k, E) =−
Z
π
Im (k, E)
[E + Re (k, E) − ξ
k
)]
2
+[Im (k, E )]
2
. (8.46)
Hence, the theory of narrow ARPES peaks is reduced to determining the self-
energy of a hole.
8.4.2 Self-energy of one-dimensional hole in a non-crossing approximation
Due to energy conservation, small polarons exist in the Bloch states at
temperatures below the optical phonon frequency T <ω
0
/2 (section 4.3.2). A
finite polaron self-energy appears due to (quasi-)elastic scattering off impurities,
a low-frequency deformation potential and spin fluctuations. First we apply the
simplest non-crossing (ladder) approximation (chapter 3) to define an analytical
(k, E). Within this approximation the self-energy is k-independent for a short-
range scattering potential like a deformation or a screened impurity potential, so
that
(E)
k
G
R
(k, E) (8.47)
where G
R
(k, E) =[E − ξ
k
− (E)]
−1
.
The hole energy spectrum is parametrized in a tight-binding model as
ξ
x,y
k
= 2t cos(k
x,y
a) − 2t
cos(k
y,x
a) − µ. (8.48)
We assume that the minima of two polaron bands (equation (8.48)), are found at
the Brillouin zone boundary in X (π, 0) and Y (0,π).
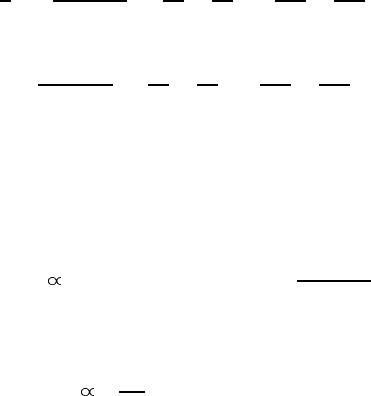
ARPES
229
As previously mentioned, the oxygen hole is (quasi-)one-dimensional due to
a large difference between the oxygen hopping integrals for the orbitals elongated
parallel to and perpendicular to the oxygen–oxygen hopping t
t. This allows
us to apply a one-dimensional approximation, reducing equation (8.48) to two
one-dimensional parabolic bands near the X and Y points, ξ
x,y
k
= k
2
/2m
∗
− µ
with m
∗
= 1/2ta
2
and k taking relative to (π, 0) and (0,π), respectively. Then,
equation (8.47) for the self-energy in the non-crossing approximation takes the
following form:
() =−2
−3/2
[() − ]
−1/2
(8.49)
for each doublet component. Here we introduce a dimensionless energy (and
self-energy), ≡ (E + µ)/
0
using
0
= (D
2
m
∗
)
1/3
as the energy unit.
The constant D is the second moment of the Gaussian white noise potential,
comprising thermal and random fluctuations as D = 2(V
2
0
T/M +n
im
α
2
),where
V
0
is the amplitude of the deformation potential, M is the elastic modulus, n
im
is
the impurity density and α is the coefficient of the δ-function impurity potential
(i.e. the strength of the scattering potential). The solution is
() =
3
−
1 + i3
1/2
2
1
16
+
3
27
+
1
256
+
3
216
1/2
1/3
−
1 − i3
1/2
2
1
16
+
3
27
−
1
256
+
3
216
1/2
1/3
. (8.50)
While the energy resolution in the present ARPES studies is almost perfect
[264], the momentum resolution remains finite in most experiments, δ>0.1π/a.
Hence, we have to integrate the spectral function (equation (8.46)) with a
Gaussian momentum resolution to obtain the experimental photocurrent:
I (k, E)
∞
−∞
dk
A
c
(k
, −E) exp
−
(k − k
)
2
δ
2
. (8.51)
The integral is expressed in terms of () and the error function w(z) as follows:
I (k, E)
−
2Z
δ
Im{()[w(z
1
) + w(z
2
)]} (8.52)
where z
1,2
=[±k − i/2()]/δ, w(z) = e
−z
2
erfc(−iz) and = (−E + µ)/
0
.
This photocurrent is plotted as broken lines in figure 8.9 for two momenta,
k = 0.04π/a (almost Y or X points of the Brillouin zone) and k = 0.3π/a.
The chemical potential is placed in the charge transfer gap below the bottom
of the hole band, µ =−20 meV, the momentum resolution is taken as δ =
0.28π/a and the damping
0
= 19 meV. The imaginary part of the self-energy
(equation (8.50)) disappears below =−3/2
5/3
−0.9449. Hence, this

230
Superconducting state of cuprates
Figure 8.9. The polaron spectral function, integrated with the momentum resolution
function for two angles, k = 0.04π/a (upper curves) and k = 0.30π/a with the damping
0
= 19 meV, the momentum resolution δ = 0.28π/a and the polaron mass m
∗
= 9.9m
e
.
The bipolaron binding energy 2|µ|=40 meV. The broken curves are the spectral density
integrated with the momentum resolution in the non-crossing approximation.
approximation gives a well-defined gap rather than a pseudogap. Actually, the
non-crossing approximation fails to describe the localized states inside the gap
(i.e. a tail of the density of states). We have to go beyond a simple ladder to
describe the single-electron tunnelling inside the gap and the ARPES spectra at
small binding energies.
8.4.3 Exact spectral function of a one-dimensional hole
The exact spectral function for a one-dimensional particle in a random Gaussian
white noise potential was calculated by Halperin [281] and the density of states
by Frisch and Lloyd [282]. Halperin derived two pairs of differential equations
from whose solutions the spectral function may be calculated:
A
c
(k,) = 4
∞
−∞
p
0
(−z) Re p
1
(z) dz. (8.53)
Here p
0,1
(z) obeys two differential equations:
d
2
dz
2
+
d
dz
(z
2
+ 2)
p
0
= 0 (8.54)
and
d
2
dz
2
+
d
dz
(z
2
+ 2) − z − ik
p
1
+ p
0
= 0 (8.55)

ARPES
231
with the boundary conditions
lim
z→∞
z
2−n
p
n
(z) = lim
z→−∞
z
2−n
p
n
(z) (8.56)
where k is measured in units of k
0
= (D
1/2
m
∗
)
2/3
. The first equation may be
integrated to give
p
0
(z) =
exp(−z
3
/3 − 2z)
z
−∞
exp(u
3
/3 + 2u) du
π
1/2
∞
0
u
−1/2
exp(−u
3
/12 − 2u) du
. (8.57)
The equation for p
1
(z) has no known analytic solution and, hence, must be solved
numerically. There is, however, an asymptotic expression for A
c
(k,) in the tail
where ||1:
A
c
(k,) 2π(−2)
1/2
exp
−
4
3
(−2)
3/2
cosh
2
πk
(−8)
1/2
. (8.58)
The result for A
c
(k, −E) integrated with the Gaussian momentum resolution
is shown in figure 8.9 for two values of the momentum (full lines). In contrast
to the non-crossing approximation, the exact spectral function (averaged with
the momentum resolution function) has a tail due to the states localized by
disorder within the normal-state gap. However, besides this tail, the non-crossing
approximation gives very good agreement and for a binding energy greater than
about 30 meV, it is practically exact.
The cumulative DOS (appendix B)
K
0
() = (2π)
−1
−∞
d
∞
−∞
dkA
p
(k,
) (8.59)
is expressed analytically [282] in terms of the tabulated Airy functions Ai(x) and
Bi(x) as
K
0
() = π
−2
[Ai
2
(−2) + Bi
2
(−2)]
−1
. (8.60)
DOS ρ() = dK
0
()/d fits well the voltage–current tunnelling characteristics of
cuprates, as discussed in section 8.2.
8.4.4 ARPES in Y124 and Y123
With the polaronic doublet (equation (8.48)) placed above the chemical potential,
we can quantitatively describe high-resolution ARPES in Y123 [279] and Y124
[278]. The exact one-dimensional polaron spectral function, integrated with
the experimental momentum resolution (shown in figure 8.10), provides a
quantitative fit to the ARPES spectra in Y124 along the Y– direction. The
angular dispersion is described with the polaron mass m
∗
= 9.9m
e
. The spectral
shape is reproduced well with
0
= 19 meV. There is also quantitative agreement
232
Superconducting state of cuprates
Figure 8.10. Theoretical ARPES spectra for the Y– direction (b). Parameters are those
of figure 8.9. The theory provides a quantitative fit to experiment (a) [278] in this scanning
direction.
Figure 8.11. Theoretical ARPES spectra in Y124 for the Y–S direction (b). The theoretical
fit agrees well with experiment (a) [278] in a restricted range of k
x
near the Y-point and,
outside this range, the theoretical peaks are somewhat higher than in experiment.

ARPES
233
Figure 8.12. Energy-integrated ARPES intensity in Y124 in the Y– (a)andY–S(b)
directions. Momenta are measured relative to the Y-point of the Brillouin zone.
between theory and experiment in the perpendicular direction Y–S, in a restricted
region of small k
x
, where almost no dispersion is observed around Y (figure 8.11).
However, there is a significant loss of the energy-integrated intensity along
both directions (figure 8.12) which the theoretical spectral function alone cannot
account for. The energy-integrated ARPES spectra obey the sum rule,
∞
−∞
dEI(k, E) |d(k)|
2
(8.61)
if the chemical potential is pinned inside the charge-transfer gap. Therefore,
we have to conclude that the dipole matrix element depends on k. The rapid
loss of the integrated intensity in the Y–S direction was interpreted by some
authors [283] as a Fermi-surface crossing. While the Fermi-surface crossing
might be compatible with our scenario (see figure 5.3(b)), it is hard to believe
that it has been really observed in Y124. Indeed, the peaks in the Y–S direction
are all 15 meV or more below the Fermi level—at a temperature of 1 meV. If the
loss of spectral weight were due to a Fermi-surface crossing, one would expect
the peaks to approach much closer to the Fermi level.
Also the experimental spectral shape of the intensity at k = k
F
is
incompatible with any theoretical scenario, including different marginal Fermi-
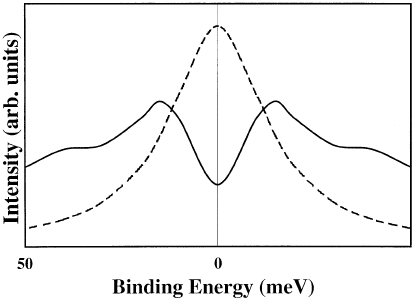
liquid models, as shown in figure 8.13. The spectral function on the Fermi surface
should be close to a simple Lorentzian:
A
c
(k
F
, E) ∼
|E|
β
E
2
+ constant × E
2β
(8.62)
because the imaginary part of the self-energy behaves as |E|
β
with 0 ≤ β ≤ 2
in a Fermi or in a marginal Fermi liquid. In contrast, the experimental intensity
234
Superconducting state of cuprates
Figure 8.13. The experimental ARPES signal (full line) on the alleged Fermi surface does
not correspond to a Fermi-liquid spectral function (broken line). We assume particle–hole
symmetry to obtain the spectral function for negative binding energy.
shows a pronounced minimum at the alleged Fermi surface (figure 8.13). If there
is indeed no Fermi-surface crossing, why then do some determinations point to
a large Fermi surface in cuprates, which is drastically incompatible with their
kinetic and thermodynamic properties? It might be due to the fact that the oxygen
hole band has its minima at large k inside or even on the boundary of the Brillouin
zone. Then ARPES show intense peaks near large k imitating a large Fermi-
surface.
8.5 Sharp increase of the quasi-particle lifetime below T
c
It has been observed at certain points in the Brillouin zone that the ARPES peak in
bismuth cuprates is relatively sharp at low temperatures in the superconduncting
state but that it almost disappears into the background above the transition [284,
285]. A very sharp increase in the quasi-particle lifetime in the superconducting
state has been observed in the thermal Hall conductivity measurements [286].
The abrupt appearence of the quasi-particle state below T
c
is also implied in the
tunnelling I –V characteristics [274,275].
Here we show that a large increase in the quasi-particle lifetime below T
c
is due to the screening of scatterers by the Bose–Einstein condensate of charged
bipolarons [203, 287]. To illustrate the point, let us calculate the scattering cross
section of a charged particle (mass m,chargee) scattered by a static Coulomb
potential V (r) screened by a charged Bose gas. The general theory of potential
scattering in terms of phase shifts was developed in the earliest days of quantum
mechanics [288]. While, in principle, this allows scattering cross sections to be
calculated for an arbitary potential, in practice the equations for the radial part

Sharp increase of the quasi-particle lifetime below
T
c
235
of the wavefunction may only be solved analytically for a few potentials and, in
the standard formulation, are not in a suitable form for numerical computation.
The ‘variable phase’ approach [289] solves this problem by taking the phase-
shift functions of the radial coordinate. The Schr¨odinger equation for each radial
component of the wavefunction then reduces to a first-order differential equation
for the corresponding phase shift.
In dimensionless units (
= 2m = 1), the Schr¨odinger equation for the radial
part of the angular momentum component (l) of the wavefunction of a particle
with wavevector k undergoing potential scattering is
u
l
(r) +[k
2
−l(l + 1)/r
2
− V (r)]u
l
(r) = 0. (8.63)
The scattering phase shift, δ
l
, is obtained by comparison with the asymptotic
relation
u
l
(r)
r→∞
−→ sin(kr − lπ/2 + δ
l
) (8.64)
and the scattering cross section is then
σ =
4π
k
2
∞
l=0
sin
2
δ
l
. (8.65)
In the variable phase method [289], we must satisfy the condition that
V (r)
r→0
−→ V
0
r
−n
(8.66)
with n < 2. The angular momentum phase shift is then
δ
l
= lim
r→∞
δ
l
(r) (8.67)
where the phase function, δ
l
(r), satisfies the phase equation
δ
l
(r) =−k
−1
V (r)[cos δ
l
(r) j
l
(kr) −sin δ
l
(r)n
l
(kr)]
2
(8.68)
with
δ
l
(r)
r→0
−→ −
V
0
r
−n
k
2
(kr)
2l+3
(2l + 3 − n)[(2l + 1)!!]
2
(8.69)
and j
l
(x ) and n
l
(x ) are the Riccati–Bessel functions. In the l = 0 case, the phase
equation reduces to
δ
0
(r) =−k
−1
V (r) sin
2
[kr + δ
0
(r)]. (8.70)
In the slow-particle limit, we may neglect higher-order contributions to the
scattering cross section, so that
σ =
4π
k
2
sin
2
δ
0
. (8.71)
