Alexandrov A.S.,Theory of Superconductivity - From Weak to Strong Coupling
Подождите немного. Документ загружается.

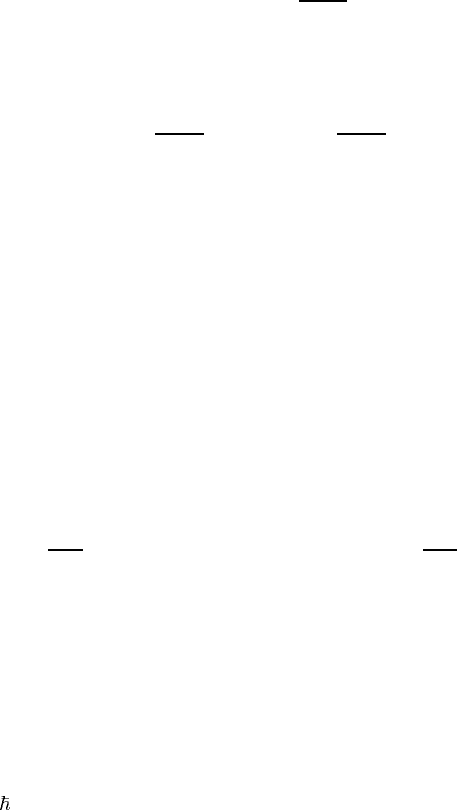
246
Bloch states
Since the volume of the reciprocal lattice primitive cell is (2π)
3
N/V ,whereV is
the volume of the crystal, k can be written in the alternative form:
k =
(2π)
3
V
. (A.14)
This allows us to replace the sum over all allowed k by an integral over the first
Brillouin zone,
k
F(k) =
V
(2π)
3
k
F(k)k =
V
(2π)
3
BZ
F(k) dk (A.15)
for any analytical function F(k). Different eigenstates of the periodic
Hamiltonian are also the eigenstates of the translation operator. Hence, they
transform under translations as
ψ
k
(r + l) = e
ik·l
ψ
k
(r). (A.16)
If we write ψ(r) in the form
ψ
k
(r) = u
k
(r)e
ik·r
(A.17)
then u
k
(r) should be periodic (u
k
(r + l) = u
k
(r)) as follows from
equation (A.16). Substituting ψ
k
(r) into the Schr¨odinger equation yields the
following equation for the periodic part of the wavefunction:
−
1
2m
e
(∇
2
+ 2ik · ∇) + V (r)
u
k
(r) =
E
k
−
k
2
2m
e
u
k
(r). (A.18)
This equation should be solved within the primitive unit cell and extended
periodically for the rest of the crystal. Just like for particles in a box, the
eigenstates of the equation are each identified by a discrete quantum number
n = 0, 1, 2,.... Hence, the eigenstates of an electron in a crystal are described
by almost continuous wavevectors k in the first Brillouin zone, and by a discrete
band index n. The wavevector, k, plays a fundamental role in the electron energy
band structure and dynamics, similar to that of the free electron momentum p.
However, although the free-electron wavevector and the momentum are the same
(if
= 1), the Bloch k is not proportional to the electron momentum on a lattice.
When acting on ψ
k
(r), the momentum operator p =−i∇ yields
−i∇ψ
k
(r) = kψ
k
(r) − ie
ik·r
∇u
k
(r) (A.19)
which is not a constant multiplied by ψ
k
(r) because of the second term. Hence,
ψ
k
(r) is not a momentum eigenstate.

Effective mass approximation
247
A.2 Effective mass approximation
Electron wavefunctions in semiconductors and narrow-band metals differ
significantly from plane waves because the periodic part of the Bloch function is
strongly modulated with a characteristic length of the order of the lattice constant.
In general, the band structure should be calculated numerically. However, in
doped semiconductors, states in the vicinity of special points of the Brillouin
zone matter only at low temperatures and doping. These are the points where the
energy dispersion, E
nk
, of the conduction (empty) band has a minimum and the
valence band dispersion has a maximum. While their positions and band edges
are determined experimentally or numerically, the energy dispersion nearby can
be calculated analytically by applying the so-called ‘k · p’ perturbation theory. To
illustrate the theory, we consider a simple cubic semiconductor with the gap E
g
,
which has a non-degenerate conduction band of s or d-like symmetry at k = 0
( point) and three p-like valence bands degenerate at k = 0 and transforming at
this point like x, y and z under the rotation of the crystal space group. There is no
spin–orbit interaction in this example, so that spin is irrelevant. According to the
Bloch theorem,
ψ
nk
(r) = e
ik·r
u
nk
(r) (A.20)
where u
nk
(r) is periodic in r. It satisfies equation (A.18). At the point k = 0,
this equation for u
n0
(r) is
−
1
2m
e
∇
2
+ V (r)
u
n0
(r) = E
n0
u
n0
(r). (A.21)
Hence, u
n0
(r) has the symmetry of the crystal space group. For a small k, one
can expand u
nk
in the series,
u
nk
(r) =
n
=s,x,y,z
a
n
k
u
n
0
(r) (A.22)
to obtain a secular equation:
det
E
g
+
k
2
2m
e
− E
k
k
x
p
m
e
k
y
p
m
e
k
z
p
m
e
k
x
p
m
e
k
2
2m
e
− E
k
00
k
y
p
m
e
0
k
2
2m
e
− E
k
0
k
z
p
m
e
00
k
2
2m
e
− E
k
= 0 (A.23)
where p ≡s|−i∇
x
|x=s|−i∇
y
|y=s|−i∇
z
|z. Different bras and kets
correspond to the four different Bloch functions u
n0
(r). There are four solutions
to this equation. Two of them correspond to the conduction (c) and light hole (lh)
valence band:
E
c,lhk
=
k
2
2m
e
+
E
g
2
±
E
2
g
4
+
k
2
p
2
m
2
e
(A.24)

248
Bloch states
N
(
F
(
OK
(
KK
Figure A.1. ‘k · p’ energy bands near the -point of the Brillouin zone in the cubic lattice.
and the other two, which are degenerate, correspond to heavy holes (hh):
E
hhk
=
k
2
2m
e
(A.25)
One can split two degenerate heavy-hole bands and change the sign of their
effective mass if one includes the states at the -point split-off from those under
consideration by an energy larger than E
g
as shown by a thin line in figure A.1.
The effective mass approximation follows from equation (A.24) for small
k m
e
E
g
/ p,
E
ck
− E
g
k
2
2m
c
(A.26)
and
E
lhk
−
k
2
2m
lh
(A.27)
where the effective mass is
m
c,lh
m
e
=
1
p
2
/(m
e
E
g
) ± 1
. (A.28)
In many semiconductors, the interband dipole moment p is large and the bandgap
is small, p
2
m
e
E
g
. Therefore, the electron and hole masses can be significantly
smaller than the free-electron mass:
m
c
m
e
m
lh
m
e
1. (A.29)
As a result, when experiment does not show heavy carriers, it does not necessarily
follow that the electron–phonon interaction is small and the renormalization of the

Tight-binding approximation
249
band mass is absent. The effective mass approximation is applied if the external
field varies slowly in time and smoothly in space. If the external or internal fields
are strong and contain high-frequency and (or) short-wave Fourier components,
they involve large momenta of the order of the reciprocal lattice constant making
all states of the electron band relevant. In this case, a tight binding approximation
is more appropriate.
A.3 Tight-binding approximation
For narrow-band semiconductors and metals, it is convenient to replace the Bloch
states by the site (Wannier) wavefunctions, defined as
w
m
(r) =
1
√
N
k
e
−ik·m
ψ
k
(r) (A.30)
where m =
j
m
j
a
j
is the lattice vector with the integer m
j
andwedropthe
band quantum number n. The Wannier wavefunctions are orthogonal,
dr w
∗
m
(r)w
n
(r) = δ
m,n
(A.31)
because the Bloch functions are orthogonal. Indeed calculating the integral in
equation (A.31), one obtains
dr w
∗
m
(r)w
n
(r) =
1
N
k
e
ik·(m−n)
. (A.32)
The sum is
k
e
ik·(m−n)
=
N
1
/2
n
1
=−N
1
/2+1
e
2πin
1
l
1
/N
1
N
2
/2
n
2
=−N
2
/2+1
e
2πin
2
l
2
/N
2
×
N
3
/2
n
3
=−N
3
/2+1
e
2πin
3
l
3
/N
3
(A.33)
where l
j
≤ N
j
− 1 are integers. Here each of the multipliers is the sum of a
geometric progression:
N
j
/2
n
j
=−N
j
/2+1
exp(2iπn
j
l
j
/N
j
) = e
iπl
i
N
j
n
j
=1
exp(2iπn
j
l
j
/N
j
)
= e
iπl
i
(e
2iπn
j
− 1) exp(2iπl
j
/N
j
)
e
2iπl
j
/N
j
− 1
. (A.34)
250
Bloch states
The denominator of this expression is not zero for any allowed l
j
, except l
j
= 0.
However, the numerator is zero because n
j
is an integer. Hence, the sum
equation (A.32) is non-zero only for m = n. In this case the sum is trivially
equal to N which proves the orthogonality of the Wannier functions. In the same
way, one can prove that
1
N
m
exp[i(k − k
) · m]=δ
kk
. (A.35)
Then multiplying equation (A.30) by exp(ik · m) and performing the sum with
respect to m, we express the Bloch state as a linear combination of the Wannier
states:
ψ
k
(r) =
1
√
N
m
e
ik·m
w
m
(r). (A.36)
If we substitute this sum into the Schr¨odinger equation and multiply it by w
∗
n
(r),
then, after integrating with respect to the electron coordinate r, the energy band
dispersion, E
k
, is expressed via the hopping integrals T (m − n) as
E
k
=
1
N
m
T (m)e
ik·m
(A.37)
where
T (m − n) =
dr w
∗
n
(r)
−
∇
2
2m
e
+ V (r)
w
m
(r). (A.38)
The idea behind the tight-binding approximation is to fit the band dispersion
calculated numerically with a finite number of hopping integrals. Many electronic
structures, in particular perovskite ones, can be fitted with only the nearest-
neighbour matrix elements between s-, p- and d-like orbitals. The hopping
integrals could not be calculated by using tabulated atomic wavefunctions and
potentials estimated for various solids. True atomic orbitals are not orthogonal for
different sites and they do not provide a quantitative description of bands in solids.
However, atomic-like Wannier orbitals (equation (A.30)) can provide a very good
description already in a tight-binding nearest-neighbour approximation. For a
non-degenerate band in a cubic lattice, the approximation yields
E
k
=
1
N
|m|=a
T (m)e
ik·m
= 2T (a)[cos(k
x
a) + cos(k
y
a) + cos(k
z
a)] (A.39)
if the middle of the band is taken as zero (T (0) = 0). If the nearest-neighbour
hopping integral, T (a), is negative, the bottom of the band is found at k = 0.
Near the bottom the dispersion is parabolic with the effective band mass
m =
1
2a
2
|T (a)|
. (A.40)

Tight-binding approximation
251
Half the bandwidth is D = z|T (a)|,wherez = 6 is the number of nearest
neighbours. Many physical properties of solids depend on the density of states
(DOS) per unit cell,
N(E) =
1
N
k
δ(E − E
k
) (A.41)
rather than on a particular dispersion E
k
. Replacing the sum by the integral, we
obtain
N(E) =
1
4π
2
|T (a)|
E
|T (a)|
(A.42)
if the dispersion is parabolic, E
k
∝ k
2
. If the dispersion is parabolic but two-
dimensional, E
k
∝ (k
2
x
+ k
2
y
), the DOS is energy independent:
N(E) =
1
4π|T (a)|
. (A.43)
Finally, for a one-dimensional parabolic spectrum (E
k
∝ k
2
x
), the DOS has a
square-root singularity near the bottom of the band:
N(E) =
1
2π|T (a)|
|T (a)|
E
. (A.44)

Appendix B
Quantum statistics and Boltzmann kinetics
B.1 Grand partition function
If the number of particles is large, the life history of a single particle is not
so important. What really determines the physical properties of a macroscopic
system is the average distribution of particles in real and momentum space.
A statistical approach combined with quantum mechanics allow for a full
description of the macroscopic system. Within this approach, we first assume
that we know the exact eigenstates |Q and energy levels U
Q
of the many-
particle system. The particles interact with the walls of their container (i.e. with
a thermostat) so as to establish a thermal equilibrium but not to such an extent
as to affect the whole set of quantum numbers Q and energy levels. Due to the
interaction with the thermostat, the energy and the total number of particles (N)
fluctuate. The system takes some time staying in every allowed quantum state Q.
The statistical probability P of finding the system in a particular quantum state
Q with the total number of particles N is proportional to this time. It depends on
U
Q
and N: P = P(U
Q
, N).
It is not hard to find the probability P(U
Q
, N) in thermal equilibrium. Let
us consider a system containing two independent parts 1 and 2 with the energies
U
1,2
and the number of particles N
1,2
, respectively. If the two parts do not interact
with each other, the probability P
1
(U
1
, N
1
) that system 1 should be in the state
U
1
, N
1
is independent of the probability P
2
(U
2
, N
2
). The probability for two
independent events to occur is equal to the product of their separate probabilities.
This means that the probability P(U, N) of finding the whole system in the state
U, N is the product of P
1
(U
1
, N
1
) and P
2
(U
2
, N
2
),
P(U, N) = P
1
(U
1
, N
1
)P
2
(U
2
, N
2
). (B.1)
The thermal equilibrium is described by a universal probability, P
1
(U, N) =
P
2
(U, N) = P(U, N), which depends only on U and N but not on the particular
system. Then taking the logarithm of both parts of equation (B.1), we obtain
ln P(U, N) = ln P(U
1
, N
1
) + ln P(U
2
, N
2
). (B.2)
252
Fermi–Dirac and Bose–Einstein distribution functions
253
The energy of non-interacting systems and the number of particles are additive:
U = U
1
+U
2
(B.3)
N = N
1
+ N
2
(B.4)
and the only possibility to satisfy equation (B.2) is given by
ln P(U, N) =−ln Z − β(U − µN) (B.5)
where Z, β and µ are independent of U and N. Hence, the equilibrium density
matrix is given by
P(U
Q
, N) = Z
−1
e
−β(U
Q
−µN)
. (B.6)
The constant Z (the grand partition function) depends on β and µ because the
probability is normalized by the condition
∞
N=0
Q
P(U
Q
, N) = 1. (B.7)
Hence, the grand partition function is obtained as
Z =
∞
N=0
Q
e
−β(U
Q
−µN)
. (B.8)
The quantity β = 1/ T is the inverse temperature. It describes the interaction with
the thermostat and determines the average energy of the macroscopic system.
Finally, the constant µ is the chemical potential. It determines the average
equilibrium number of particles in an open system.
B.2 Fermi–Dirac and Bose–Einstein distribution functions
The quantum statistics of non-interacting identical particles is readily derived
using the grand partition function. The quantum state of an ideal Fermi or Bose
gas is fully described by the numbers n
ν
of identical particles in every single-
particle quantum state |ν. This means that proper quantum numbers of the
whole gas are different sets of the occupation numbers of single-particle states,
Q ={n
ν
},wheren
ν
= 0, 1 for fermions and n
ν
= 0, 1, 2,...,∞ for bosons.
The energy levels are given by
U
Q
=
ν
E
ν
n
ν
(B.9)
and the total number of particles is
N =
ν
n
ν
. (B.10)

254
Quantum statistics and Boltzmann kinetics
Here E
ν
are the single-particle energy levels. The average energy and the average
number of particles of a gas depend on the average values ¯n
ν
of the occupation
numbers of each single-particle state. The distribution function
¯n
ν
=
Q
n
ν
P(U
Q
, N
Q
) (B.11)
can be expressed as
¯n
ν
=−
1
Zβ
∞
N=0
Q
∂
∂ E
ν
exp
− β
ν
n
ν
(E
ν
− µ)
=−
∂ ln Z
∂ E
ν
. (B.12)
The partition function is readily obtained by using
Z =
{n
ν
}
ν
e
−βn
ν
(E
ν
−µ)
=
ν
n
ν
e
−βn
ν
(E
ν
−µ)
. (B.13)
In the case of fermions, there are only two terms in the sum with n
ν
= 0and
n
ν
= 1, and
Z =
ν
[1 +e
−β(E
ν
−µ)
]. (B.14)
Hence the (Fermi–Dirac) distribution of ideal fermions is
¯n
F
ν
=
1
e
β(E
ν
−µ)
+ 1
. (B.15)
The partition function of ideal bosons is determined by the sum of the geometric
progression as
∞
n
ν
=0
e
−βn
ν
(E
ν
−µ)
=
1
1 − e
−β(E
ν
−µ)
(B.16)
and the (Bose–Einstein distribution) of ideal bosons is
¯n
B
ν
=
1
e
β(E
ν
−µ)
− 1
.
B.3 Ideal Fermi gas
B.3.1 Fermi energy
The density of states (DOS) (per unit of volume) of a single particle in a
macroscopic box is proportional to its kinetic energy E = k
2
/(2m) in a power
depending on the dimensionality d of the box (appendix A.3):
N(E)
E
(d−2)/2
. (B.17)

Ideal Fermi gas
255
If we place N
F
non-interacting fermions with the spin-
1
2
into a box of volume L
d
,
their total energy U and particle density n (= N
F
/L
d
)aregivenby
U = 2
dEN(E)
E
e
β(E−µ)
+ 1
(B.18)
and
n = 2
dEN(E)
1
e
β(E−µ)
+ 1
. (B.19)
Here, 2 takes into account the degeneracy of every orbital state due to the spin.
Let us calculate these integrals at zero temperature. The chemical potential should
be positive at T = 0, otherwise the Fermi–Dirac distribution function would be
zero for any positive E.Forµ>0andβ →∞, the distribution is a step function
1
e
β(E−µ)
+ 1
≈ (E
F
− E) (B.20)
where E
F
≡ µ(0) is the Fermi energy, and (x) = 1forx > 0 and zero
otherwise. Calculating the integrals with a step-like distribution yields
E
F
=
(3π
2
n)
2/3
2m
(B.21)
E
F
=
πn
m
E
F
=
π
2
n
2
8m
for a three-, two- and one-dimensional box, respectively, and the total energy
U
n
(d+2)/d
.
B.3.2 Specific heat
At almost all temperatures of interest, T remains much smaller than the Fermi
temperature of ordinary metals, T
F
= E
F
/k
B
1000 K. Following Sommerfeld,
we can expand the total energy in powers of T/T
F
to calculate the electron
contribution to the specific heat of a metal. Let us introduce a function of energy
defined as
K
r
(E) =
E
−∞
dE
N(E
)E
r
. (B.22)
In particular K
0
(E) represents the cumulative DOS, which is the number of states
with an energy less than E. Then integrating by parts, the integral
∞
−∞
dEN(E)
E
r
e
β(E−µ)
+ 1
becomes
β
4
∞
−∞
dE
K
r
(E)
cosh
2
[β(E − µ)/2]
. (B.23)
