Alexandrov A.S.,Theory of Superconductivity - From Weak to Strong Coupling
Подождите немного. Документ загружается.


216
Superconducting state of cuprates
expect ν ≥ 1 and a substantial contribution from delocalized bipolarons moving
principally in two dimensions and thus, that λ increases linearly with temperature,
as observed [254]. However, heavy-ion bombardment [257] introduces rather
deep and narrow potential wells for which we might expect ν<1. This would
explain the upturn in the temperature dependence of λ in the disordered films
[257].
8.2 SIN tunnelling and Andreev reflection
There is compelling experimental evidence that the pairing of carriers takes place
well above T
c
in cuprates (chapter 6), the clearest being uniform susceptibility
[186, 267] and tunnelling [265]. The gap in tunnelling and photoemission
is almost temperature independent below T
c
[265, 268] and exists above T
c
[265, 269–271]. Kinetic [198] and thermodynamic [272] data suggest that the
gap opens in both charge and spin channels at any relevant temperature in a wide
range of doping. At the same time, reflection experiments, in which an incoming
electron from the normal side of a normal/superconducting contact is reflected
as a hole along the same trajectory (section 2.13), revealed a much smaller gap
edge than the bias at the tunnelling conductance maxima in a few underdoped
cuprates [273]. Other tunnelling measurements [274, 275] also showed distinctly
different superconducting- and normal-state gaps.
In the framework of bipolaron theory, we can consider a simplified model,
which describes the temperature dependence of the gap and tunnelling spectra
in cuprates and accounts for two different energy scales in the electron-hole
reflection [260]. The assumption is that the attraction potential in cuprates
is large compared with the (renormalized) Fermi energy of polarons. The
model is a generic one-dimensional Hamiltonian including the kinetic energy of
carriers in the effective mass (m
∗
) approximation and a local attraction potential,
V (x − x
) =−U δ(x − x
),as
H =
s
dx ψ
†
s
(x )
−
1
2m
∗
d
2
dx
2
− µ
ψ
s
(x )
−U
dx ψ
†
↑
(x )ψ
†
↓
(x )ψ
↓
(x )ψ
↑
(x ) (8.16)
where s =↑, ↓ is the spin. The first band in cuprates to be doped is the
oxygen band inside the Hubbard gap (section 5.2). This band is quasi-one-
dimensional as discussed in section 5.4, so that a one-dimensional approximation
(equation (8.16)) is a realistic starting point. Solving a two-particle problem
with the δ-function potential, one obtains a bound state with the binding energy
2
p
= m
∗
U
2
/4 and with the radius of the bound state r = 2/(m
∗
U).We
assume that this radius is less than the inter-carrier distance in cuprates. It is then
that real-space bipolarons are formed. If three-dimensional corrections to the
energy spectrum of pairs are taken into account, the ground state of the system is

SIN tunnelling and Andreev reflection
217
the Bose–Einstein condensate (BEC). The chemical potential is pinned below the
band edge by about
p
both in the superconducting and normal states, so that the
normal state single-particle gap is
p
.
Now we take into account that in the superconducting state (T < T
c
)
single-particle excitations interact with the condensate via the same potential U.
Applying the Bogoliubov approximation (section 2.2) we reduce the Hamiltonian
(8.16) to a quadratic form:
H =
s
dx ψ
†
s
(x )
−
1
2m
∗
d
2
dx
2
− µ
ψ
s
(x )+
dx [
c
ψ
†
↑
(x )ψ
†
↓
(x )+H.c.]
(8.17)
where the coherent pairing potential,
c
=−Uψ
↓
(x )ψ
↑
(x ), is proportional
to the square root of the condensate density,
c
= constant × n
1/2
c
(T ).The
single-particle excitation energy spectrum, E(k), is found using the Bogoliubov
transformation as
E(k) =[(k
2
/2m
∗
+
p
)
2
+
2
c
]
1/2
(8.18)
if one assumes that the condensate density does not depend on position. This
spectrum is quite different from the BCS quasi-particles because the chemical
potential is negative with respect to the bottom of the single-particle band,
µ =−
p
. The single-particle gap, /2, defined as the minimum of E(k),is
given by
/2 =[
2
p
+
2
c
(T )]
1/2
. (8.19)
It varies with temperature from (0)/2 =[
2
p
+
2
c
(0)]
1/2
at zero temperature
down to the temperature-independent
p
above T
c
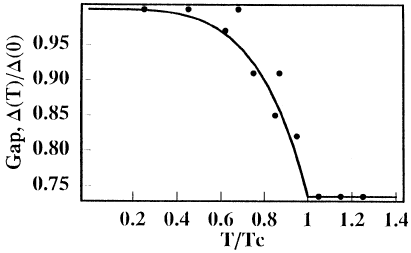
. The theoretical temperature
dependence, equation (8.19), describes well the pioneering experimental
observation of the anomalous gap in YBa
2
Cu
3
O
7−δ
in the electron-energy-loss
spectra by Demuth et al [277] (figure 8.3) with
2
c
(T ) =
2
c
(0) ×[1 −(T / T
c
)
n
]
below T
c
and zero above T
c
,andn = 4. We note that n = 4 is an exponent which
is expected in the two-fluid model of any superfluid [276].
A normal metal–superconductor (SIN) tunnelling conductance via a
dielectric contact, dI /dV is proportional to the density of states, ρ(E),ofthe
spectrum (equation (8.18)). Taking into account the scattering of single-particle
excitations by a random potential, as well as thermal lattice and spin fluctuations
(see section 8.4.3), one finds, at T = 0
dI /dV = constant ×
ρ
2eV −
0
+ Aρ
−2eV −
0
(8.20)
with
ρ(ξ) =
4
π
2
×
Ai(−2ξ)Ai
(−2ξ) +Bi(−2ξ)Bi
(−2ξ)
[Ai
2
(−2ξ) + Bi
2
(−2ξ)]
2
(8.21)
A is an asymmetry coefficient, explained in [259], Ai(x) and Bi(x ) the Airy
functions and
0
is the scattering rate.
218
Superconducting state of cuprates
Figure 8.3. Temperature dependence of the gap (equation (8.19) (line)) compared with the
experiment [277] (dots) for
p
= 0.7(0).
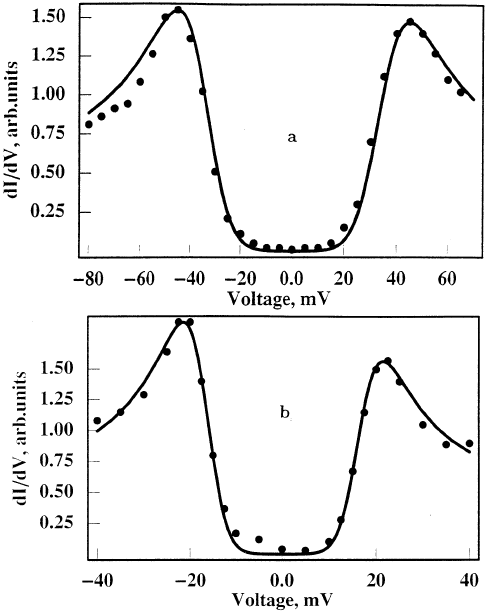
We compare the conductance (equation (8.20)) with one of the best
STM spectra measured in Ni-substituted Bi
2
Sr
2
CaCu
2
O
8+x
single crystals by
Hancottee et al [268] in figure 8.4(a). This experiment shows anomalously
large /T
c
> 12 with the temperature dependence of the gap similar to
that in figure 8.3 below T
c
. The theoretical conductance (equation (8.20))
describes well the anomalous gap/T
c
ratio, injection/emission asymmetry, zero-
bias conductance at zero temperature and the spectral shape inside and outside
the gap region. There is no doubt that the gap (figure 8.4(a)) is s-like. The
conductance (equation (8.20)) also fits well the conductance curve obtained on
‘pure’ Bi-2212 single crystals, as shown in figure 8.4(b), while a simple d-wave
BCS density of states cannot describe the excess spectral weight in the peaks and
the shape of the conductance outside the gap region. We note that the scattering
rate,
0
, is apparently smaller in the ‘pure’ sample than in the Ni-substituted
sample, as expected.
A simple theory of tunnelling into a bosonic (bipolaronic) superconductor
in a metallic (no-barrier) regime follows from this model. As in the canonical
BCS approach applied to normal metal–superconductor tunnelling by Blonder
et al [47], the incoming electron produces only outgoing particles in the
superconductor (x > l), allowing for a reflected electron and (Andreev) hole
in the normal metal (x < 0) (section 2.13). There is also a buffer layer of the
thickness l at the normal metal–superconductor boundary (x = 0), where the
chemical potential with respect to the bottom of the conduction band changes
gradually from a positive large value µ in metal to a negative value −
p
in
a bosonic superconductor. We approximate this buffer layer by a layer with a
constant chemical potential µ
b
(−
p
<µ
b
<µ) and with the same strength of
the pairing potential
c
as in a bulk superconductor. The Bogoliubov equations
may be written as usual (section 2.13), with the only difference being that the
chemical potential with respect to the bottom of the band is a function of the
SIN tunnelling and Andreev reflection
219
Figure 8.4. Theoretical tunnelling conductance (equation (8.20) (line)) compared with the
experimental STM conductance (dots) in (a) Ni-substituted Bi
2
Sr
2
CaCu
2
O
8+x
[268] with
= 90 meV, A = 1.05,
0
= 40 meV and (b) in ‘pure’ Bi-2212 [268] with = 43 meV,
A = 1.2and
0
= 18 meV.
coordinate x:
Eψ(x) =
−(1/2m) d
2
/dx
2
− µ(x)
c
c
(1/2m) d
2
/dx
2
+ µ(x)
ψ(x). (8.22)
Thus, the two-component wavefunction in normal metal is given by
ψ
n
(x < 0) =
1
0
e
iq
+
x
+ b
1
0
e
−iq
+
x
+ a
0
1
e
−iq
−
x
(8.23)
220
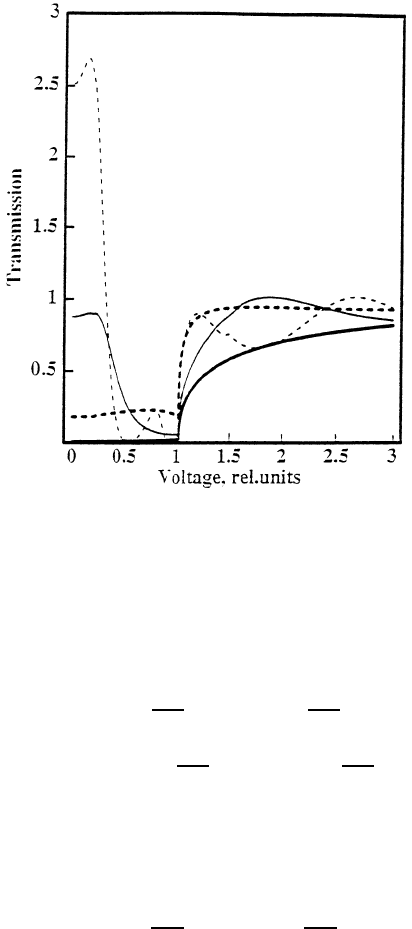
Superconducting state of cuprates
Figure 8.5. Transmission versus voltage (measured in units of
p
/e)for
c
= 0.2
p
,
µ = 10
p
, µ
b
= 2
p
and l = 0 (bold line), l = 1 (bold dashes), l = 4 (thin line), and
l = 8 (thin dashes) (in units of 1/(2m
p
)
1/2
).
while in the buffer layer, it has the form
ψ
b
(0 < x < l) = α
1
c
E+ξ
e
ip
+
x
+ β
1
c
E−ξ
e
−ip
−
x
+ γ
1
c
E+ξ
e
−ip
+
x
+ δ
1
c
E−ξ
e
ip
−
x
(8.24)
where the momenta associated with the energy E are q
±
=[2m(µ ± E)]
1/2
and
p
±
=[2m(µ
b
± ξ)]
1/2
with ξ = (E
2
−
2
c
)
1/2
. A well-behaved solution in the
superconductor with a negative chemical potential is given by
ψ
s
(x > l) = c
1
c
E+ξ
e
ik
+
x
+ d
1
c
E−ξ
e
ik
−
x
(8.25)
where the momenta associated with the energy E are k
±
=[2m(−
p
± ξ)]
1/2
.
The coefficients a, b, c, d,α,β,γ,δ are determined from the boundary
conditions, which are the continuity of ψ(x) and its derivatives at x = 0and
x = l. Applying the boundary conditions and carrying out an algebraic reduction,
SIN tunnelling and Andreev reflection
221
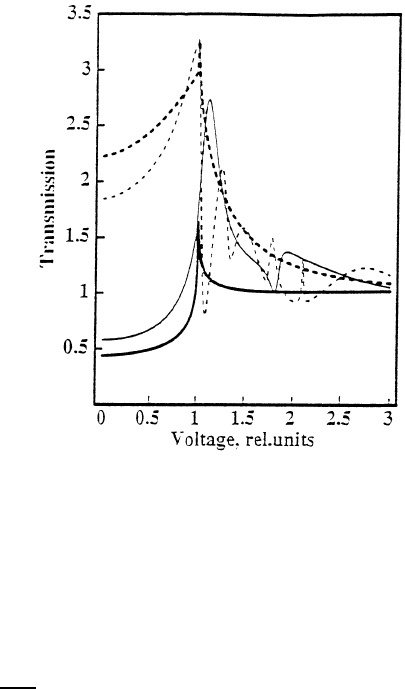
Figure 8.6. Transmission versus voltage (measured in units of
c
/e)for
p
= 0.2
c
,
µ = 10
c
, µ
b
= 2
c
and l = 0 (bold line), l = 1 (bold dashes), l = 4 (thin line), and
l = 8 (thin dashes) (in units of 1/(2m
c
)
1/2
).
we find
a = 2
c
q
+
( p
+
f
−
g
+
− p
−
f
+
g
−
)/D (8.26)
b =−1 +
2q
+
D
[(E + ξ) f
+
(q
−
f
−
− p
−
g
−
) − (E − ξ) f
−
(q
−
f
+
− p
+
g
+
)]
(8.27)
with
D = (E + ξ)(q
+
f
+
+ p
+
g
+
)(q
−
f
−
− p
−
g
−
)
− (E − ξ)(q
+
f
−
+ p
−
g
−
)(q
−
f
+
− p
+
g
+
) (8.28)
and
f
±
= p
±
cos(p
±
l) − ik
±
sin( p
±
l) (8.29)
g
±
= k
±
cos( p
±
l) − i p
±
sin( p
±
l).
The transmission coefficient in the electrical current, 1 +|a|
2
−|b|
2
is shown
in figure 8.5 for different values of l, when the coherent gap
c
is smaller than the
pair-breaking gap
p
and in figure 8.6 in the opposite case,
p
<
c
.Inthefirst

222
Superconducting state of cuprates
case, figure 8.5, we find two distinct energy scales, one is
c
in the subgap region
due to the electron-hole reflection and the other one is /2, which is a single-
particle band edge. However, there is only one gap,
c
, which can be seen in the
second case, figure 8.6. We note that the transmission has no subgap structure if
the buffer layer is absent (l = 0) in both cases. In the extreme case of a wide
buffer layer, l (2m
p
)
−1/2
(figure 8.5) or l (2m
c
)
−1/2
(figure 8.6), there
are some oscillations of the transmission due to the bound states inside the buffer
layer.
We expect that
p
c
in underdoped cuprates (figure 8.5) while
p
≤
c
in optimally doped cuprates (figure 8.6). Thus, the model accounts for two
different gaps experimentally observed in Giaver tunnelling and electron-hole
reflection in underdoped cuprates and for a single gap in optimally doped samples
[273]. An oscillating structure, observed in underdoped YBa
2
Cu
3
O
7−δ
[273], is
also found in the theoretical conductance at finite l (figure 8.5). The transmissions
(figures 8.5 and 8.6) are due to a coherent tunnelling into the condensate and
into a single-particle band of the bosonic superconductor. There is an incoherent
transmission into localized single-particle impurity states and into incoherent
(‘supracondensate’) bound pair states as well, which might explain a significant
featureless background in the subgap region [273].
8.3 SIS tunnelling
Within the standard approximation [76], the tunnelling current, I (V ), between
two parts of a superconductor separated by an insulating barrier is proportional
to a convolution of the Fourier component of the single-hole retarded Green’s
function, G
R
(k,ω), with itself as
I (V ) ∝
k, p
∞
−∞
dω Im G
R
(k,ω)Im G
R
( p, e|V |−ω) (8.30)
where V is the voltage in the junction.
The problem of a hole on a lattice coupled with the bosonic field of lattice
vibrations has a solution in terms of the coherent (Glauber) states in the strong-
coupling limit, λ>1, where the Migdal–Eliashberg theory cannot be applied
(section 4.3.4),
G
R
(k,ω) = Z
∞
l=0
q
1
,...,q
l
"
l
r=1
|γ(q
r
)|
2
(2N)
l
l!(ω −
l
r=1
ω
q
r
− (k +
l
r=1
q
r
) + iδ)
.
(8.31)
The hole energy spectrum, (k), is renormalized due to the polaron narrowing of
the band and (in the superconducting state) also due to interaction with the BEC
of bipolarons as discussed in section 8.2,
(k) =[ξ
2
(k) +
2
c
]
1/2
. (8.32)

SIS tunnelling
223
Here ξ(k) = Z
E(k) − µ is the renormalized polaron band dispersion with
the chemical potential µ and E(k) =
m
T (m) exp(−ik · m) is the bare band
dispersion in a rigid lattice.
Quite differently from the BCS superconductor, the chemical potential µ is
negative in the bipolaronic system, so that the edge of the single-hole band is
found above the chemical potential at −µ =
p
. Near the edge the parabolic
one-dimensional approximation for the oxygen hole is applied, compatible with
the ARPES data [262],
k
k
2
x
2m
∗
+ /2. (8.33)
Differently from the canonical Migdal–Eliashberg Green function (chapter 3),
there is no damping (‘dephasing’) of low-energy polaronic excitations in
equation (8.31) due to the electron–phonon coupling alone. This coupling leads
to a coherent dressing of low-energy carriers by phonons, which is seen in the
Green fucntion as phonon sidebands with l ≥ 1.
However, elastic scattering by impurities yields a finite life-time for the
Bloch polaronic states. For the sake of analytical transparency, here we model this
scattering as a constant imaginary self-energy, replacing iδ in equation (8.31) by
a finite i/2. In fact, the ‘elastic’ self-energy can be found explicitly as a function
of energy and momentum (see section 8.4.3). Its particular energy/momentum
dependence is essential in the subgap region of tunnelling, where it determines
the value of zero-bias conductance. However, it hardly plays any role in the peak
region and higher voltages.
Substiting equation (8.33) into equations (8.31) and (8.30), and performing
the intergration with respect to frequency and both momenta, we obtain for the
tunnelling conductance, σ(V ) = dI /dV ,
σ(V ) ∝
∞
l,l
=0
q,q
"
l
r=1
"
l
r
=1
|γ(q
r
)|
2
|γ(q
r
)|
2
(2N)
l+l
l!l
!
× L
e|V |− −
l
r=1
ω
q
r
−
l
r
=1
ω(q
r
),
(8.34)
where L[x ,]=/(x
2
+
2
). To perform the remaining integrations and
summations, we introduce a model analogue of the Eliashberg spectral function
(α
2
F(ω) (section 3.4)) by replacing the q-sums in equation (8.34) by
1
2N
q
|γ(q)|
2
A(ω
q
) =
g
2
π
dω L[ω − ω
0
,δω]A(ω) (8.35)
for any arbitrary function of the phonon frequency A(ω
q
).Inthiswaywe
introduce the characteristic frequency, ω
0
, of phonons strongly coupled with
holes, their average number g
2
in the polaronic cloud and their dispersion δω.

224
Superconducting state of cuprates
As soon as δω is less than ω
0
, we can extend the integration over phonon
frequencies from −∞ to ∞ and obtain
σ(V ) ∝
∞
l,l
=0
g
2(l+l
)
l!l
!
L[e|V |− − (l + l
)ω
0
,+ δω(l +l
)]. (8.36)
By replacing the Lorentzian in equation (8.36) by the Fourier integral, we
perform the summation over l and l
with the final result for the conductance as
follows:
σ(V ) ∝
∞
0
dt exp[2g
2
e
−δωt
cos(ω
0
t) − t]
× cos[2g
2
e
−δωt
sin(ω
0
t) − (e|V |−)t]. (8.37)
From the isotope effect on the carrier mass, phonon densities of states,
experimental values of the normal-state pseudogap and the residual resistivity
(chapters 6 and 7), one estimates the coupling strength g
2
to be of the order of one,
the characteristic phonon frequency about 30–100 meV, the phonon frequency
dispersion about a few tens meV, the gap /2 about 30–50 meV and the impurity
scattering rate of the order of 10 meV.
The SIS conductance (equation (8.37)) calculated with parameters in this
range is shown in figure 8.7 for three different values of coupling. The
conductance shape is remarkably different from the BCS density of states, both
s-wave and d-wave. There is no Ohm’s law in the normal region, e|V | >,
the dip/hump features (due to phonon sidebands) are clearly seen already in the
first derivative of the current, there is a substantial incoherent spectral weight
beyond the quasi-particle peak for the strong coupling, g
2
≥ 1, and there is
an unusual shape for the quasi-particle peaks. All these features as well as the
temperature dependence of the gap are beyond BSC theory no matter what the
symmetry of the gap is. However, they agree with the experimental SIS tunnelling
spectra in cuprates [265,268,269,274,275]. In particular, the theory quantitatively
describes one of the best tunnelling spectra obtained on Bi
2
Sr
2
CaCu
2
O
8+δ
single
crystals by the break-junction technique [268] (figure 8.8). Some excess zero-
bias conductance compared with the experiment is due to our approximation of
the ‘elastic’ self-energy. The exact (energy-dependent) self-energy provides an
agreement in this subgap region as well, as shown in figure 8.9. The dynamic
conductance of Bi-2212 mesas [274] at low temperatures is almost identical to
the theoretical one in figure 8.7 for g
2
= 0.5625.
The unusual shape of the main peaks (figure 8.8) is a simple consequence
of the (quasi-)one-dimensional hole density of states near the edge of the oxygen
band. The coherent (l = l
= 0) contribution to the current with no elastic
scattering ( = 0) is given by
I
0
∝
∞
d
( − /2)
1/2
∞
d
(
− /2)
1/2
δ( +
− e|V |) (8.38)
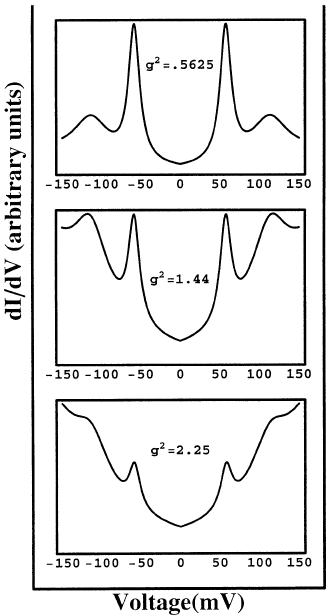
SIS tunnelling
225
Figure 8.7. SIS tunnelling conductance in a bipolaronic superconductor for different
values of the electron–phonon coupling, g
2
,and/2 = 29 meV, ω
0
= 55 meV,
δω = 20 meV, = 8.5meV.
so that the conductance is a δ function:
σ
0
(V ) ∝ δ(e|V |−). (8.39)
Hence, the width of the main peaks in the SIS tunnelling (figure 8.8) measures the
elastic scattering rate directly.
The disappearance of the quasi-particle sharp peaks above T
c
in Bi-cuprates
can also be explained in the framework of bipolaron theory. Below T
c
, bipolaronic
condensate provides an effective screening of the long-range (Coulomb) potential
of impurities, while above T
c
the scattering rate might increase by many times
(section 8.5). This sudden increase in in the normal state washes out sharp peaks
from tunnelling and ARPES spectra. The temperature-dependent part,
c
(T ),
of the total gap (equation (8.19)) is responsible for the temperature shift of the
