Alexandrov A.S.,Theory of Superconductivity - From Weak to Strong Coupling

Подождите немного. Документ загружается.

206

Superconducting transition

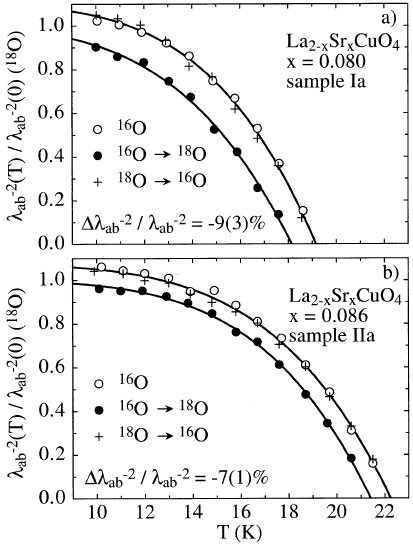
Figure 7.3. The isotope effect on the magnetic ﬁeld penetration depth in two samples of

2−x

CuO

[173] (courtesy of J Hofer).

α>0.5 [230], and a small negative value of α was found in Bi-2223 [231].

Essential features of the isotope effect, in particular large values in low-T

cuprates, an overall trend to lower value as T

increases [232] and a small or even

negative α in some high-T

cuprates were understood using equations (4.225) and

(4.226) for the isotope exponents of (bi)polaronic superconductors [82]. With

increasing ion mass, the bipolaron mass increases and the BEC temperature T

decreases in the bipolaronic superconductor. In contrast, an increase in the ion

mass leads to band narrowing and an enhancement of the polaron density of

states and to an increase in T

in polaronic superconductors. Hence, the isotope

exponent in T

can distinguish the BCS-like polaronic superconductivity with

α<0 and the BEC of small bipolarons with α>0. Moreover, underdoped

cuprates, which are deﬁnitely in the BEC regime (section 5.3), could have α>0.5

(equation (4.226)) as observed.

Another prediction of the bipolaron theory is an isotope effect on the carrier

mass (equation (4.222)) which is linked with the isotope effect on T

, according

to equations (4.224) and (4.226).

Speciﬁc heat anomaly

207

Remarkably, this prediction was experimentally conﬁrmed by Zhao et al

[173] providing compelling evidence for polaronic carriers in doped cuprates.

The effect was observed in the London penetration depth of isotope-substituted

cuprates (ﬁgure 7.3). The carrier density is unchanged with the isotope

substitution of O

by O

, so that the isotope effect on λ

directly measures

the isotope’s effect on the carrier mass. In particular, the carrier mass isotope

exponent α

= dlnm

∗∗

/dlnM was found to be as large as α

= 0.8in

1.895

0.105

CuO

. Then, according to equation (4.222), the polaron mass

enhancement should be m

∗∗

/m  5 in this material. Using equation (5.27),

we obtain an in-plane bipolaron mass as large as m

∗∗

≈ 10m

with the bare

hopping integral T (NNN) = 0.2 eV. The in-plane magnetic ﬁeld penetration

depth, calculated with this mass is λ

=[m

∗∗

/8πne

]

1/2

≈ 316 nm, where n is

the hole density. This agrees well with the experimental one, λ

 320 nm.

Using the measured values of λ

= 320 nm, λ

= 4160 nm and R

4 ×10

−3

−1

(just above T

), we obtain T

= 31 K in astonishing agreement

with the experimental value T

= 30 K in this compound.

7.3 Speciﬁc heat anomaly

Bose liquids (or, more precisely,

He) show the characteristic λ-point singularity

in their speciﬁc heat but superﬂuid Fermi liquids like BCS superconductors

exhibit a sharp second-order phase transition accompanied by a ﬁnite jump in

the speciﬁc heat (section 2.6). It was established beyond doubt [233–237] that the

anomaly in high-T

cuprates differs qualitatively from the BSC prediction. As was

stressed by Salamon et al [238], the heat capacity is logarithmic near the transition

and, consequently, cannot be adequately treated by mean-ﬁeld BCS theory even if

the Gaussian ﬂuctuations are included. In particular, estimates using the Gaussian

ﬂuctuations yield an unusually small coherence volume (table 7.3), comparable

with the unit cell volume [234] and Gi number (equation (1.53)) of the order of

one.

Table 7.3. Coherence volume  in

, the in-plane ξ

and out-of-plane ξ

coherence

lengths derived from a Ginzburg–Landau analysis of the speciﬁc heat [234].

Compound ξ

(

)ξ

(

YBa

400 125 3.2

YBa

7−0.025

309 119 2.6

YBa

7−0.05

250 119 2.1

YBa

7−0.1

143 119 1.2

0.8

0.2

0.5

84 70 1.2

1.8

2.2

40 <0.9

208

Superconducting transition

2.5

3.0

3.5

4.0

4.5

.4 .6 .8 1.0 1.2 1.4

0.01

0.03

0.1

0.2

0.3

T/T

-1.0

-.8

-.6

-.4

-.2

.4 .6 .8 1.0 1.2 1.4

0.01

0.03

0.1

0.2

0.3

(T)

T/T

C(H,T)-C(0,T)

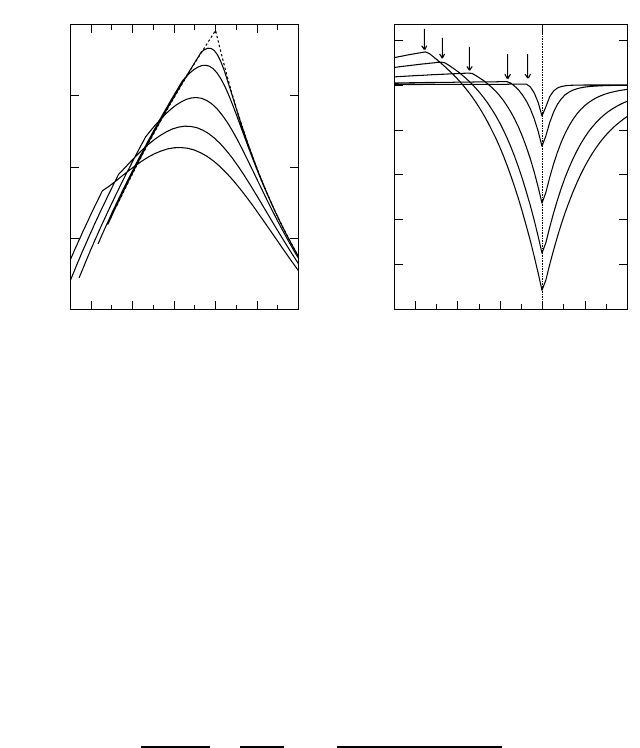
Figure 7.4. Temperature dependence of the speciﬁc heat divided by temperature (arbitrary

units) of the charged Bose gas scattered off impurities for several ﬁelds (ω

= 2eB/m

∗∗

(b) shows two anomalies, the lowest one traces the resistive transition, while the highest

anomaly is the normal-state feature.

The magnetic ﬁeld dependence of the anomaly [239] is also unusual but

it can be described by the bipolaron model [240, 241]. Calculations of the

speciﬁc heat of charged bosons in a magnetic ﬁeld require an analytical DOS,

N(, B) of a particle, scattered by other particles and/or by a random potential of

impurities. We can use the DOS in a magnetic ﬁeld with an impurity scattering

as in section 4.7.8, which allows for an analytical result (equation (4.266)). The

speciﬁc heat coefﬁcient

C(T, B)

T dT



d

N(, B)

exp[( − µ)/T ]−1

calculated with this DOS and with µ determined from n



d N(, B) f () is

showninﬁgure7.4.

The broad maximum at T  T

is practically the same as in an ideal Bose

gas without scattering [240] (appendix B.4.2). It barely shifts in the magnetic

ﬁeld. However, there is a second anomaly at lower temperatures, which is absent

in the ideal gas. This shifts with the magnetic ﬁeld, tracing precisely the resistive

transition (section 7.4), as clearly seen from the difference between the speciﬁc

heat in the ﬁeld and zero-ﬁeld curve, ﬁgure 7.4(b). The speciﬁc heat (ﬁgure 7.4)

has a striking resemblance with the Geneva group’s experiments on DyBa

andonYBa

[239], where both anomalies were observed. Within the

bipolaron model, when the magnetic ﬁeld is applied, it hardly changes the

Universal upper critical ﬁeld of unconventional superconductors

209

temperature dependence of the chemical potential near the zero-ﬁeld T

because

the energy spectrum of thermally excited bosons is practically unchanged. This is

because their characteristic energy (of the order of T

) remains huge compared

with the magnetic energy of the order of 2eB/m

∗∗

. In contrast, the energy

spectrum of low-energy bosons is strongly perturbed even by a weak magnetic

ﬁeld. As a result the chemical potential ‘touches’ the band edge at lower

temperatures, while having almost the same ‘kink’-like temperature dependence

around T

as in a zero ﬁeld. While the lower anomaly corresponds to the true long-

range order due to BEC, the higher one is just a ‘memory’ about the zero-ﬁeld

transition. This microscopic consideration shows that a genuine phase transition

into a superconducting state is related to a resistive transition (section 7.4) and to

the lower speciﬁc heat anomaly, while the broad higher anomaly is the normal-

state feature of the bosonic system in an external magnetic ﬁeld. Differing from

the BCS superconductor, these two anomalies are well separated in the bosonic

superconductor at any ﬁeld but zero.

7.4 Universal upper critical ﬁeld of unconventional

superconductors

The upper critical ﬁeld (H

(T ) = 

/2πξ(T )

) is very different in a BCS

superconductor (section 1.6.4) and in a charged Bose gas (section 4.7.8). While

(T ) is linear in temperature near T

in the Landau theory of second-order

phase transitions, it has a positive curvature (H

(T ) (T

− T )

3/2

) in a CBG.

Also at zero temperature, H

(0) is normally below the Pauli pair-breaking limit

given by H

 1.84T

(in tesla) in the BCS theory but the limit can be exceeded

by many times in CBG.

In cuprates [241–247], spin-ladders [248] and organic superconductors

[249], high-magnetic ﬁeld studies revealed a non-BCS upward curvature of

resistive H

(T ). When measurements were performed on low-T

unconventional

superconductors [243, 244, 246, 248, 249], the Pauli limit was exceeded several

times. A nonlinear temperature dependence in the vicinity of T

was

unambigously observed in a few samples [241, 245–247]. Importantly, a

thermodynamically determined H

turned out to be much higher than the

resistive H

[250] due to the contrasting magnetic ﬁeld dependences of the

speciﬁc heat anomaly and of resistive transition.

We believe that many unconventional superconductors are in the ‘bosonic’

limit of preformed real-space bipolarons, so their resistive H

is actually a

critical ﬁeld of the BEC of charged bosons [121]. Calculations carried out for

the heat capacity of a CBG in section 7.3 led to the conclusion that the resistive

and the thermodynamically determined H

are very different in bosonic

superconductors. While the magnetic ﬁeld destroys the condensate of ideal

bosons, it hardly shifts the speciﬁc heat anomaly as observed.

A comprehensive scaling of resistive H

measurements in unconventional

210

Superconducting transition

0 .2 .4 .6 .8 1.0

T/T

(T)/H

.001

.01

.01 .1 1

Tl-2201

Bi-2201

(TMTSF)

LSCO

YBCO+Zn

2-x

CuO

4-y

Bi-2212

YBCO-123

1-T/T

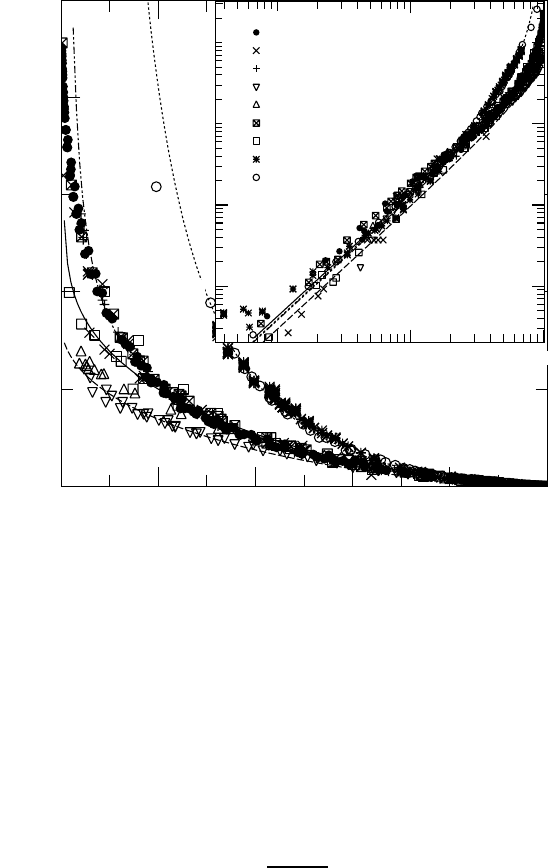
Figure 7.5. Resistive upper critical ﬁeld (determined at 50% of the transition) of

cuprates, spin-ladders and organic superconductors scaled according to equation (7.9). The

parameter b is 1 (dots), 0.02 (chain), 0.0012 (full curve), and 0 (dashes). The inset shows

a universal scaling of the same data near T

on the logarithmic scale.

superconductors is shown in ﬁgure 7.5 [241] in the framework of the microscopic

model of charged bosons scattered off impurities (section 4.7.8). The generalized

equation (4.261), accounting for a temperature dependence of the number of

delocalized bosons n

(T ), can be written as follows:

(T ) = H



(T )

)

− t

1/2



3/2

(7.8)

where T

is the zero-ﬁeld critical temperature and t = T /T

.Asshown

in section 4.7.8, the scaling constant H

depends on the mean-free path l,

= 

/2πξ

, with the characteristic (coherence) length ξ

 (l/n

))

1/4

In the vicinity of T

, one obtains a parameter-free H

(T ) ∝ (1 − t)

3/2

using equation (7.8) but the low-temperature behaviour depends on a particular

scattering mechanism and a detailed structure for the density of localized states.

Universal upper critical ﬁeld of unconventional superconductors

211

As suggested by the normal-state Hall measurements in cuprates (section 6.1),

(T ) can be parametrized as n

(T ) = n

(0) +constant × T ,sothatH

(T ) can

be described by a single-parameter expression:

(T ) = H



b(1 −t)

+ 1 − t

1/2



3/2

. (7.9)

The parameter b is proportional to the number of delocalized bosons at zero

temperature. We expect that this expression is applied in the whole temperature

region except at ultra-low temperatures, where the Fermi–Dirac golden rule in

the scaling fails. Exceeding the Pauli pair-breaking limit readily follows from the

fact that the singlet-pair binding energy is related to the normal-state pseudogap

temperature T

∗

, rather than to T

. T

∗

is higher than T

in bosonic superconductors

and cuprates (ﬁgure 5.6).

The universal scaling of H

near T

is conﬁrmed by resistive measurements

of the upper critical ﬁeld of many cuprates, spin-ladders, and organic

superconductors, as shown in ﬁgure 7.5. All measurements reveal a universal

(1 − t)

3/2

behaviour in a wide temperature region (inset), when they are ﬁtted by

equation (7.9). The low-temperature behaviour of H

(T )/H

is not universal but

well described using the same equation with the single ﬁtting parameter, b.The

parameter is close to one in high-quality cuprates with a very narrow resistive

transition [247]. It naturally becomes rather small in overdoped cuprates where

randomness is more essential, so almost all bosons are localized (at least in one

dimension) at zero temperature.

Chapter 8

Superconducting state of cuprates

Independent observations of normal-state pseudogaps in a number of magnetic

and kinetic measurements (chapter 6) and unusual critical phenomena (chapter 7)

tell us that many cuprates may not be BCS superconductors. Indeed their

superconducting state is as anomalous as the normal one. In particular,

there is strong evidence for a d-like order parameter (changing sign when

the CuO

plane is rotated by π/2) in cuprates [251]. A number of phase-

sensitive experiments [252] provide unambiguous evidence in this direction;

furthermore, the low-temperature magnetic penetration depth [253, 254] was

found to be linear in a few cuprates as expected for a d-wave BCS superconductor.

However, superconductor–insulator–normal metal (SIN) and superconductor–

insulator–superconductor (SIS) tunnelling studies (sections 8.2 and 8.3), the c-

axis Josephson tunnelling [255] and some high-precision magnetic measurements

[256] show a more usual s-like symmetry or even reveal an upturn in the

temperature dependence of the penetration depth below some characteristic

temperature [257]. Also both angle-resolved photoemission spectroscopy

(ARPES) [264] and scanning tunnelling microscopy (STM) [265] have shown

that the maximum energy gap is many times larger and the 2/T

ratio is well

above that expected in weak-coupling BCS theory (∼3.5) or in its intermediate-

coupling generalization (chapter 3).

Strong deviations from the Fermi/BCS-liquid behaviour are suggestive of a

new electronic state in cuprates, which is a charged Bose liquid of bipolarons.

In this chapter we discuss the low-temperature London penetration depth [258],

tunnelling [259–261] and ARPES [262], the symmetry of the order parameter and

superconducting stripes [263] in the framework of the bipolaron theory.

8.1 Low-temperature penetration depth

If the total number of bipolarons in one unit cell is x/2ofwhichn

are in localized

states and n

are in delocalized states, then the number in the condensate n

x − n

− n

(8.1)

212

Low-temperature penetration depth

213

and the London penetration depth λ ∝ 1/

√

. Taking the delocalized bipolarons

to be a three-dimensional gas, we have n

∝ T

3/2

. Thus in the low-temperature

limit, we can neglect n

and make the approximation

≈ x/2 − n

. (8.2)

In this limit, λ(T ) − λ(0) is small and so

λ(T ) − λ(0) ∝ n

(T ) − n

(0) (8.3)

i.e. λ has the same temperature dependence as n

. For small amounts of disorder

delocalized bipolarons may contribute to the low-temperature dependence of

λ(T ) as well; for non-interacting bipolarons moving in d dimensions, this would

give λ ∝ T

d/2

In our picture, interacting bosons ﬁll up all the localized single-particle

states in a random potential and Bose-condense into the ﬁrst extended state at

the mobility edge, E

. For convenience we choose E

= 0. When two or more

charged bosons are in a single localized state of energy E, there may be signiﬁcant

Coulomb energy and we take this into account as follows. The localization length

ξ is thought to depend on E via

ξ ∝

(−E)

(8.4)

where ν>0. The Coulomb potential energy of p charged bosons conﬁned within

aradiusξ can be expected to be

potential energy 

4 p( p −1)e



. (8.5)

Thus, the total energy of p bosons in a localized state of energy E is taken to be

w(E) = pE + p( p − 1)κ(−E)

(8.6)

where κ>0. We can thus deﬁne an energy scale E

= κ

1/(1−ν)

. (8.7)

From here on we choose our units of energy such that E

= 1. We take the total

energy of charged bosons in localized states to be the sum of the energies of the

bosons in individual potential wells. The partition function Z for such a system

is then the product of the partition functions z(E) for each of the wells,

z(E) = e

αp

∞



p=0

−α(p−p

)

(8.8)

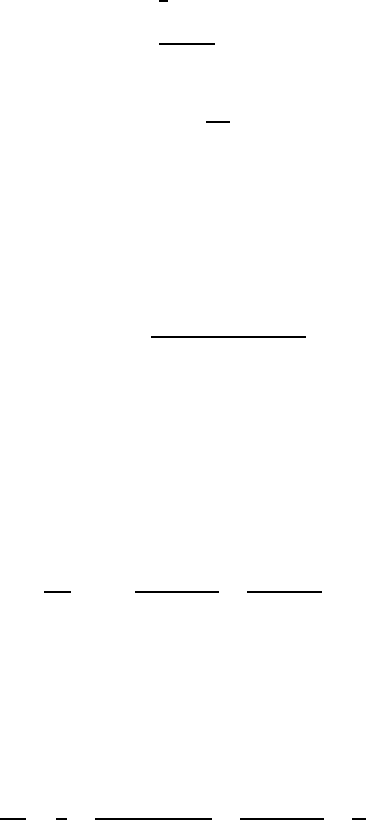
214

Superconducting state of cuprates

where

{1 + (−E)

1−ν

} (8.9)

α =

(−E)

(8.10)

and

θ =

. (8.11)

The average number of bosons in localized states n



−∞

dE pN

(E) (8.12)

where the mean occupancy p of a single localized state is taken to be

p=



∞

p=0

−α(p−p

)



∞

p=0

−α(p−p

)

(8.13)

and N

(E) is the one-particle density of localized states per unit cell below the

mobility edge (section 5.5).

We now focus on the temperature dependence of n

at low temperature

(θ  1) for the case where the (dimensionless) width of the impurity tail γ is

large (γ>1). We note that the parameter γ is the ratio of the width of the tail to

the characteristic Coulomb repulsion, E

. In the following, we consider the case

ν>1ﬁrstandthenν<1. If ν>1, we can approximate n

≈ 1 +

ν − 1

2(2 −ν)γ

2θ

(2 − ν)γ

ln 2. (8.14)

So we expect n

to be close to the total number of wells N

and to increase

linearly with temperature. Figure 8.1(a) compares this analytical formula with

an accurate numerical calculation for the case ν = 1.5, γ = 20. We also note

that even when γ<1, n

(θ) will still be linear with the same slope provided

θ  γ .Ifν<1 we obtain, keeping only the lowest power of θ (valid provided

1/ν

 θ )

(2 −ν)γ

1−ν

1 − ν

2(2 − ν)γ

−

ln 2. (8.15)

Hence, in this case, n

decreases linearly with increasing temperature (in the

low-temperature limit). Figure 8.1(b) compares this analytical formula with the

numerical calculation for the case ν = 0.65, γ = 20. We note that such

a value of ν is typical for amorphous semiconductors [266]. A large value

of γ is also expected in disordered cuprates with their large static dielectric

constant.

Low-temperature penetration depth

215

Figure 8.1. Dependence of the density of localized bosons n

on temperature θ for

γ = 20: (a) ν = 1.5, (b) ν = 0.65. The full lines correspond to the low-temperature

predictions from equations (8.14) and (8.15) while the broken lines are derived from an

accurate numerical calculation.

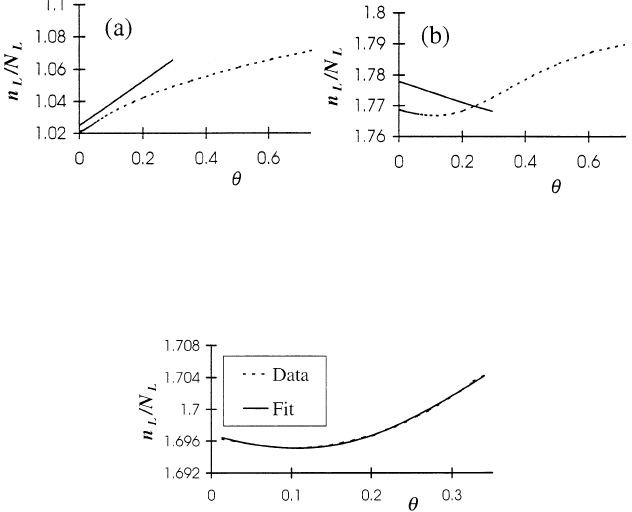
Figure 8.2. Fit to the London penetration depth measured by Walter et al [257] for a

YBCO ﬁlm. The parameter values from the ﬁt were E

= 74 K, γ = 20 and ν = 0.67.

Figure 8.2 shows that the low-temperature experimental data [257] on the

London penetration depth λ of YBCO ﬁlms can be ﬁtted very well by this theory

with ν<1. It is more usual to see λ increase linearly with temperature [253,254]

and this would correspond to ν>1 (or to the predominance of the effect of

delocalized bipolarons moving in two dimensions). We believe that ν<1is

more probable for a rapidly varying random potential while ν ≥ 1ismore

likely for a slowly varying one. Both ν<1andν ≥ 1 are observed in doped

semiconductors [266]. Hence, it is not surprising that a drastically different low-

temperature dependence of the London penetration depth is observed in different

samples of doped cuprates. In the framework of this approach, λ(T ) is related

to the localization of carriers at low temperatures rather than to any energy scale

characteristic of the condensate or to its symmetry. The excitation spectrum of the

charged Bose liquid determines, however, the temperature dependence of λ(T ) at

higher temperatures.

The key parameter of the temperature dependence of the London penetration

depth is the exponent ν of the localization length of bosons. Experimentally, the

more usual linear increase of λ with temperature is observed in samples which

either have no disorder or a shallow and smooth random potential proﬁle. Here we