Alexandrov A.S.,Theory of Superconductivity - From Weak to Strong Coupling
Подождите немного. Документ загружается.


176
Competing interactions in unconventional superconductors
Here u
j
(q, t) ≡ u
j
(q) exp(−iω
q
t) and n
q
= 0, 1, 2,...the phonon occupation
numbers. Calculating the bracket in equation (5.15), one obtains
...=T
2
pd
e
−g
2
pd
e
−g
2
dp
exp
−
q
[u
d
(q) − u
p
(q)][u
∗
p
(q) − u
∗
d
(q)]e
−iω
q
t
.
(5.17)
If ω
q
is q-independent the integral in equation (5.15) is calculated by the
expansion of the exponent in equation (5.17) as
σ
(2)
pp
=−
T
2
pd
E
g
e
−g
2
pd
e
−g
2
dp
∞
k=0
(−1)
k
(
q
[u
d
(q) − u
p
(q)][u
∗
p
(q) − u
∗
d
(q)])
k
k!(1 +kω
0
/E
g
)
.
(5.18)
Then equation (5.13) is obtained in the limit E
g
ω
0
. Equation (5.14) yields
g
2
pp
=
E
p
ω
0
1 −
Si(q
d
m)
q
d
m
, (5.19)
if we approximate the Brillouin zone by a sphere of the radius q
d
(the Debye
approximation). Here
Si(x) =
x
0
dt
sin t
t
m = a/
√
2andm = a for the in-plane oxygen–oxygen, and for apex–apex
narrowing factors, respectively. In cuprates with q
d
≈ 0.7
˚
A
−1
and a 3.8
˚
A
one obtains g
2
pp
≈ 0.2E
p
/ω
0
for an in-plane hopping, and g
2
≈ 0.3E
p
/ω
0
for
an apex–apex one. Hence, both band-narrowing factors are much less than one
can expect in the Holstein model.
The bipolaron hopping integral, t, is obtained by projecting the Hamiltonian
(5.10) onto a reduced Hilbert space containing only empty or doubly occupied
elementary cells and averaging the result with respect to phonons. The
wavefunction of an apex bipolaron localized, let us say, in the cell m is written as
|m=
4
i=1
A
i
c
†
i
c
†
apex
|0 (5.20)
where i denotes the p
x,y
orbitals and spins of the four plane oxygen ions in the
cell (figure 5.4) and c
†
apex
is the creation operator for the hole on one of the three
apex oxygen orbitals with the spin, which is the same or opposite of the spin of
the in-plane hole depending on the total spin of the bipolaron. The probability
amplitudes A
i
are normalized by the condition |A
i
|=1/2, if four plane orbitals
p
x1
, p
y2
, p
x3
and p
y4
are involved or by |A
i
|=1/
√
2 if only two of them are
relevant.
The matrix element of the Hamiltonian (5.10) of first order with respect to the
transfer integral responsible for the bipolaron tunnelling to the nearest-neighbour
cell m + a is
t =m|
˜
H|m + a=|A
i
|
2
T
apex
pp
e
−g
2
(5.21)

Bipolaron bands in high-
T
c
perovskites
177
where T
apex
pp
e
−g
2
is a single-polaron hopping integral between two apex ions. As
a result, the hole bipolaron energy spectrum consists of two bands E
x,y
(K ),
formed by an overlap of p
x
and p
y
apex polaron orbitals, respectively, as in
equation (4.269). In this equation t is the renormalized hopping integral between
p orbitals of the same symmetry elongated in the direction of the hopping (ppσ)
and t
is the renormalized hopping integral in the perpendicular direction (ppπ).
Their ratio t/t
= T
apex
pp
/T
apex
pp
= 4 as follows from the tables of hopping
integrals in solids. Two different bands are not mixed because T
apex
p
x
, p
y
= 0
for the nearest neighbours. The random potential does not mix them either if
it varies smoothly on the lattice scale. Hence, we can distinguish ‘x’and‘y’
bipolarons with a lighter effective mass in the x or y direction, respectively. The
apex z bipolaron, if formed is approximately four times less mobile than x and
y bipolarons. The bipolaron bandwidth is of the same order as the polaron one,
which is a specific feature of the inter-site bipolarons (section 4.6). For a large
part of the Brillouin zone near (0,π) for ‘x’and(π, 0) for ‘y’ bipolarons, one
can adopt the effective mass approximation
E
x,y
K
=
K
2
x
2m
∗∗
x,y
+
K
2
y
2m
∗∗
y,x
(5.22)
with K
x,y
taken relative to the band bottom positions and m
∗∗
x
= 1/t, m
∗∗
y
=
4m
∗∗
x
.
5.4.2 In-plane bipolarons
Here we consider a two-dimensional lattice of ideal octahedra that can be
regarded as a simplified model of the copper–oxygen perovskite layer as shown in
figure 5.4. The lattice period is a = 1 and the distance between the apical sites and
the central plane is h = a/2 = 0.5. For mathematical transparency, we assume
that all in-plane atoms, both copper and oxygen, are static but apical oxygens are
independent three-dimensional isotropic harmonic oscillators, so that the model
Hamilonian of section 4.6.3 is applied. Due to poor screening, the hole–apical
interaction is purely Coulombic:
g
ν
(m − n) =
κ
ν
|m − n|
2
where ν = x, y, z. To account for the experimental fact that z-polarized phonons
couple to holes stronger than others [172], we choose κ
x
= κ
y
= κ
z
/
√
2. The
direct hole–hole repulsion is
V
c
(n − n
) =
V
c
√
2|n − n
|
so that the repulsion between two holes in the nearest-neighbour (NN)
configuration is V
c
. We also include the bare NN hopping T
NN
, the next nearest
178
Competing interactions in unconventional superconductors
neighbour (NNN) hopping across copper T
NNN
and the NNN hopping between
the pyramids T
NNN
. The polaron shift is given by the lattice sum (4.148) which,
after summation over polarizations, yields
E
p
= 2κ
2
x
ω
0
m
1
|m − n|
4
+
h
2
|m − n|
6
= 31.15κ
2
x
ω
0
(5.23)
where the factor two accounts for two layers of apical sites. For reference, the
Cartesian coordinates are n = (n
x
+
1
2
, n
y
+
1
2
, 0), m = (m
x
, m
y
, h) and
n
x
, n
y
, m
x
, m
y
are integers. The polaron–polaron attraction is
V
ph
(n − n
) = 4ω
0
κ
2
x
m
h
2
+ (m − n
) · (m − n)
|m − n
|
3
|m − n|
3
. (5.24)
Performing the lattice summations for the NN, NNN and NNN
configurations
one finds V
ph
= 1.23E
p
, 0.80E
p
and 0.82E
p
, respectively. As a result, we obtain
a net inter-polaron interaction as v
NN
= V
c
− 1.23E
p
, v
NNN
=
V
c
√
2
− 0.80E
p
,
v
NNN
=
V
c
√
2
− 0.82E
p
and the mass renormalization exponents as g
2
NN
=
0.38(E
p
/ω
0
), g
2
NNN
= 0.60(E
p
/ω
0
) and (g
NNN
)
2
= 0.59(E
p
/ω
0
).
Let us now discuss different regimes of the model. At V
c
> 1.23E
p
,no
bipolarons are formed and the system is a polaronic Fermi liquid. The polarons
tunnel in the square lattice with NN hopping t = T
NN
exp(−0.38E
p
/ω
0
) and
NNN hopping t
= T
NNN
exp(−0.60E
p
/ω
0
).(Sinceg
2
NNN
≈ (g
NNN
)
2
one can
neglect the difference between NNN hoppings within and between the octahedra.)
A single-polaron spectrum is, therefore,
E
1
(k) =−E
p
− 2t
[cos k
x
+ cos k
y
]−4t cos(k
x
/2) cos(k
y
/2). (5.25)
The polaron mass is m
∗
= 1/(t +2t
). Since in general t > t
, the mass is mostly
determined by the NN hopping amplitude t.
If V
c
< 1.23E
p
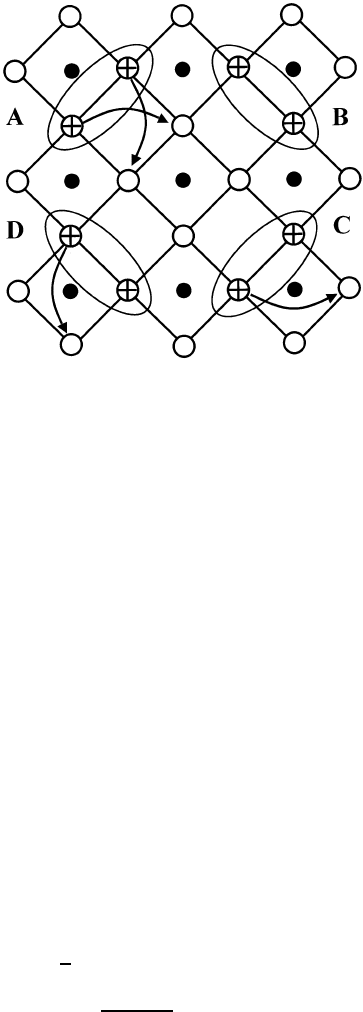
then inter-site NN bipolarons form. The bipolarons tunnel in
the plane via four resonating (degenerate) configurations A, B, C and D, as shown
in figure 5.5.
In the first order in the renormalized hopping integral, one should retain
only these lowest-energy configurations and discard all the processes that involve
configurations with higher energies. The result of such a projection is a bipolaron
Hamiltonian:
H
b
= (V
c
− 3.23E
p
)
l
[A
†
l
A
l
+ B
†
l
B
l
+ C
†
l
C
l
+ D
†
l
D
l
]
− t
l
[A
†
l
B
l
+ B
†
l
C
l
+ C
†
l
D
l
+ D
†
l
A
l
+ H.c.]
− t
n
[A
†
l−x
B
l
+ B
†
l+y
C
l
+ C
†
l+x
D
l
+ D
†
l−y
A
l
+ H.c.] (5.26)
Bipolaron bands in high-
T
c
perovskites
179
Figure 5.5. Four degenerate in-plane bipolaron configurations A, B, C and D. Some
single-polaron hoppings are indicated by arrows.
where l numbers octahedra rather than individual sites, x = (1, 0) and y = (0, 1).
A Fourier transformation and diagonalization of a 4×4 matrix yields the bipolaron
spectrum:
E
2
(k) = V
c
− 3.23E
p
± 2t
[cos(k
x
/2) ± cos(k
y
/2)]. (5.27)
There are four bipolaronic sub-bands combined in the band of width 8t
.The
effective mass of the lowest band is m
∗∗
= 2/t
. The bipolaron binding energy
is ≈ 1.23E
p
− V
c
. The bipolaron already moves in the first order of polaron
hopping. This remarkable property is entirely due to the strong on-site repulsion
and long-range electron–phonon interaction that leads to a non-trivial connectivity
of the lattice. This fact combines with a weak renormalization of t
yielding a
superlight bipolaron with the mass m
∗∗
∝ exp(0.60E
p
/ω). We recall that in the
Holstein model m
∗∗
∝ exp(2E
p
/ω) (section 4.6.1). Thus the mass of the Fr¨ohlich
bipolaron in the perovskite layer scales approximately as a cubic root of that of
the Holstein one.
With an even stronger e–ph interaction, V
c
< 1.16E
p
, NNN bipolarons
become stable. More importantly, holes can now form three- and four-particle
clusters. The dominance of the potential energy over kinetic in the transformed
Hamiltonian enables us to readily investigate these many-polaron cases. Three
holes placed within one oxygen square have four degenerate states with the energy
2(V
c
− 1.23E
p
) + V
c
/
√
2 − 0.80E
p
. The first-order polaron hopping processes
mix the states resulting in a ground-state linear combination with the energy
E
3
= 2.71V
c
− 3.26E
p
−
√
4t
2
+ t
2
. Itisessentialthatbetweenthesquares
such triads could move only in higher orders of polaron hopping. In the first order,

180
Competing interactions in unconventional superconductors
they are immobile. A cluster of four holes has only one state within a square of
oxygen atoms. Its energy is E
4
= 4(V
c
− 1.23E
p
) + 2(V
c
/
√
2 − 0.80E
p
) =
5.41V
c
− 6.52E
p
. This cluster, as well as all bigger ones, are also immobile
in first-order polaron hopping. We would like to stress that at distances much
larger than the lattice constant the polaron–polaron interaction is always repulsive
(section 4.4) and the formation of infinite clusters, stripes or strings is strictly
prohibited (section 8.6). We conclude that at V
c
< 1.16E
p
, the system quickly
becomes a charge segregated insulator.
The fact that within the window, 1.16E
p
< V
c
< 1.23E
p
, there are no three
or more polaron bound states means that bipolarons repel each other. The system
is effectively a charged Bose gas, which is a superconductor (section 4.7). The
superconductivity window, that we have found, is quite narrow. This indicates
that the superconducting state in cuprates requires a rather fine balance between
electronic and ionic interactions.
5.5 Bipolaron model of cuprates
The considerations set out in sections 5.2, 5.3 and 5.4 leads us to a simple model
of cuprates [179]. The main assumption is that all electrons are bound into small
singlet and triplet inter-site bipolarons stabilized by e–ph and spin–fluctuation
interactions. As the undoped plane has a half-filled Cu3d
9
band, there is no
space for bipolarons to move if they are inter-site. Their Brillouin zone is half the
original electron one and is completely filled with hard-core bosons. Hole pairs,
which appear with doping, have enough space to move, and they are responsible
for low-energy kinetics. Above T
c
a material such as YBa
2
Cu
3
O
6+x
contains a
non-degenerate gas of hole bipolarons in singlet and triplet states. Triplets are
separated from singlets by a spin-gap J and have a lower mass due to a lower
binding energy (figure 5.6). The main part of the electron–electron correlation
energy (Hubbard U and inter-site Coulomb repulsion) and the electron–phonon
interaction are taken into account in the binding energy of bipolarons , and in
their band-width renormalization as described in chapter 4. When the carrier
density is small (n
b
1 (as in cuprates)), bipolaronic operators are almost
bosonic (section 4.7.1). The hard-core interaction does not play any role in
this dilute limit, so only the Coulomb repulsion is relevant. This repulsion is
significantly reduced due to a large static dielectric constant in oxides (
0
1). Hence, carriers are almost-free charged bosons and thermally excited non-
degenerate fermions, so that the canonical Boltzmann kinetics (section 1.1) and
the Bogoliubov excitations of the charged Bose gas (section 4.7.3) are perfectly
applied in the normal and superconducting states, respectively.
The population of singlet, n
s
,tripletn
t
and polaron, n
p
bands is determined
by the chemical potential µ ≡ T ln y,wherey is found using the thermal
equilibrium of singlet and triplet bipolarons and polarons:
2n
s
+ 2n
t
+ n
p
= x. (5.28)

Bipolaron model of cuprates
181
Figure 5.6. Bipolaron picture of high-temperature superconductors. A indicates
degenerate singlet and triplet inter-site bipolarons. B shows non-degenerate singlet and
triplet inter-site bipolaron, which naturally includes the addition of an extra excitation
band. The crosses are copper sites and the circles are oxygen sites. w is the half-bandwidth
of the polaron band, t is the half-bandwidth of the bipolaronic bands, /2 is the bipolaron
binding energy per polaron and J is the exchange energy per bipolaron.
Applying the effective-mass approximation for quasi-two-dimensional energy
spectra of all particles, we obtain for 0
y < 1:
−m
∗∗
s
ln(1 − y) − 3m
∗∗
t
ln(1 − ye
−J/T
) + m
∗
ln(1 + y
1/2
e
−/(2T )
) =
π x
T
(5.29)
in the normal state, and y = 1 in the superconducting state. Here x is the total
number of holes per unit area. If the polaron energy spectrum is (quasi-)one-
dimensional (as in section 6.5), an additional T
−1/2
appears in front of the
logarithm in the third term on the left-hand side of equation (5.29).
We should also take into account localization of holes by a random potential,
because doping inevitably introduces some disorder. The Coulomb repulsion
182
Competing interactions in unconventional superconductors
restricts the number of charged bosons in each localized state, so that the
distribution function will show a mobility edge E
c
[194]. The number of bosons in
a single potential well is determined by the competition between their long-range
Coulomb repulsion (
4e
2
/ξ ) and the binding energy, E
c
− . If the localization
length diverges with the critical exponent ν<1 (ξ ∼ (E
c
− )
−ν
), we can
apply a ‘single-well–single-particle’ approximation assuming that there is only
one boson in each potential well (see also section 8.1). Within this approximation
localized charged bosons obey the Fermi–Dirac statistics, so that their density is
given by
n
L
(T ) =
E
c
−∞
N
L
(E) dE
y
−1
exp(E/T ) + 1
(5.30)
where N
L
(E) is the density of localized states. Near the mobility edge, it remains
constant N
L
(E) n
L
/γ , where γ is of the order of the binding energy in a single
random potential well, and n
L
is the number of localized states per unit area. The
number of empty localized states turns out to be linear as a function of temperature
in a wide temperature range T
γ from equation (5.30). Then the conservation
of the total number of carriers yields for the chemical potential:
π(x − 2n
L
)
T
=−m
∗∗
s
ln(1 − y) − 3m
∗∗
t
ln(1 − ye
−J/T
)
+ m
∗
ln(1 + y
1/2
e
−/(2T )
) −
2πn
L
γ
ln(1 + y
−1
). (5.31)
If the number of localized states is about the same as the number of pairs
(n
L
≈ x /2), a solution of this equation does not depend on temperature in a
wide temperature range above T
c
. With y to be a constant (y ≈ 0.6inawide
range of parameters in equation (5.31)), the number of singlet bipolarons in the
Bloch states is linear in temperature:
n
s
(T ) = (x /2 − n
L
) + T
n
L
γ
ln(1 + y
−1
). (5.32)
The numbers of triplets and polarons are exponentially small at low temperatures,
T J,.
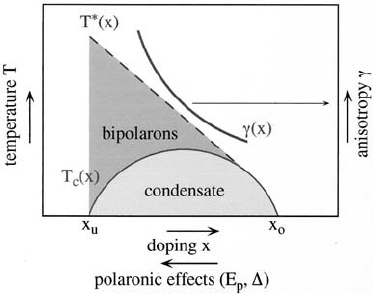
The model suggests a phase diagram of the cuprates as shown in figure 5.7.
This phase diagram is based on the assumption that to account for the high
values of T
c
in cuprates, one has to consider electron–phonon interactions
larger than those used in the intermediate-coupling theory of superconductivity
(chapter 3). Regardless of the adiabatic ratio, the Migdal–Eliashberg theory of
superconductivity and the Fermi-liquid theory break at λ ≈ 1(section4.2). A
many-electron system collapses into a small (bi)polaron regime at λ ≥ 1 with
well-separated vibration and charge-carrier degrees of freedom. Even though
it seems that these carriers should have a mass too large to be mobile, the
inclusion of the on-site Coulomb repulsion and a poor screening of the long-range
electron–phonon interaction leads to mobile inter-site bipolarons (section 4.6).
Bipolaron model of cuprates
183
Figure 5.7. Phase diagram of superconducting cuprates in the bipolaron theory (courtesy
of J Hofer).
Above T
c
, the Bose gas of these bipolarons is non-degenerate and below T
c
,their
phase coherence sets in and hence superfluidity of the double-charged 2e bosons
occurs. Of course, there are also thermally excited single polarons in the model
(figure 5.6).
There is much evidence for the crossover regime at T
∗
and normal-state
charge and spin gaps in cuprates (chapter 6). These energy gaps could be
understood as half of the binding energy and the singlet–triplet gap of
preformed bipolarons, respectively [185] and T
∗
is a temperature, where the
polaron density compares with the bipolaron one. Further evidence for bipolarons
comes from a parameter-free estimate of the renormalized Fermi energy
F
,which
yields a very small value as discussed in section 5.3. There might be a crossover
from the Bose–Einstein condensation to a BCS-like polaronic superconductivity
(section 4.5) across the phase diagram [179]. If the Fermi liquid does exist at
overdoping, then it is likely that the heavy doping causes an ‘overcrowding effect’
where polarons find it difficult to form bipolarons due to a larger number of
competing holes. Many experimental observations can be explained using the
bipolaron model (chapters 6, 7 and 8).

Chapter 6
Normal state of cuprates
6.1 In-plane resistivity and Hall ratio
Thermally excited phonons and (bi)polarons are well decoupled in the strong-
coupling regime of the electron–phonon interaction (chapter 4), so that the
standard Boltzmann equation of section 1.1 for renormalized carriers is applied.
We make use of the τ approximation [193] in an electric field E = ∇φ, a
temperature gradient ∇T and in a magnetic field B ⊥ E, ∇T . Bipolaron and
single-polaron non-equilibrium distributions are found to be
f (k) = f
0
(E) + τ
∂ f
0
∂ E
v ·{F + n × F} (6.1)
where
F = (E − µ)∇T / T + ∇(µ − 2eφ)
f
0
(E) =[y
−1
exp(E/T ) − 1]
−1
for bipolarons with the energy E = k
2
/(2m
∗∗
) and with the Hall angle =
b
= 2eBτ
b
/m
∗∗
and
F = (E + /2 − µ/2)∇T/T + ∇(µ/2 −eφ)
f
0
(E) ={y
−1/2
exp[(E + /2)/T ]+1}
−1
E = k
2
/(2m
∗
) and =
p
= eBτ
p
/m
∗
for thermally excited polarons. Here
n = B/B is a unit vector in the direction of the magnetic field. The Hall angles
areassumedtobesmall( 1), because the polarons and bipolarons are heavy.
Equation (6.1) is used to calculate the electrical and thermal currents induced by
the applied thermal and potential gradients:
j
α
= a
αβ
∇
β
(µ − 2eφ) + b
αβ
∇
β
T (6.2)
w
α
= c
αβ
∇
β
(µ − 2eφ) + d
αβ
∇
β
T. (6.3)
184

In-plane resistivity and Hall ratio
185
Equation (6.2) defines the current with the polaronic conductivity σ
p
=
e
2
τ
p
n
p
/m
∗
, where kinetic coeffficents are given by
a
xx
= a
yy
=
1
2e
σ
p
(1 + 4A) (6.4)
a
yx
=−a
xy
=
1
2e
σ
p
(
p
+ 4A
b
)
b
xx
= b
yy
=
σ
p
e
[
p
+
− µ
2T
+ 2A(
b
− µ/T )]
b
yx
=−b
xy
=
σ
p
e
p
p
+
− µ
2T
+ 2A
b
(
b
− µ/T )
.
Equation (6.3) defines the heat flow with coefficients given by
c
xx
= c
yy
=
σ
p
2e
2
[T
p
+ /2 +eφ + 2A(T
b
+ 2eφ)] (6.5)
c
yx
=−c
xy
=
σ
p
2e
2
[
p
(T
p
+ /2 +eφ) + 2A
b
(T
b
+ 2eφ)]
d
xx
= d
yy
=
σ
p
e
2
T γ
p
+
p
( − µ/2 + eφ) + (/2 + eφ)
− µ
2T
+ A[T γ
b
+
b
(2eφ − µ) − 2eφµ/T ]
d
yx
=−d
xy
=
σ
p
e
2
p
T γ
p
+
p
( − µ/2 +eφ) + (/2 +eφ)
− µ
2T
+ A
b
[T γ
b
+
b
(2eφ − µ) − 2eφµ/T )]
.
Here
=
∞
0
dEE
2
∂ f
0
/∂ E
T
∞
0
dEE∂ f
0
/∂ E
=
2(z, 2, 1)
(z, 1, 1)
(6.6)
and
γ =
∞
0
dEE
3
∂ f
0
/∂ E
T
2
∞
0
dEE∂ f
0
/∂ E
=
6(z, 3, 1)
(z, 1, 1)
are numerical coefficients, expressed in terms of the Lerch transcendent
(z, s, a) =
∞
k=0
z
k
(a + k)
s
with z = y in
b
, γ
b
and z =−y
1/2
exp[−/(2T )] in
p
, γ
p
,
A =
m
∗
τ
b
n
b
m
∗∗
τ
p
n
p
(6.7)
