Alexandrov A.S.,Theory of Superconductivity - From Weak to Strong Coupling

Подождите немного. Документ загружается.

146

Strong-coupling theory

phonon frequency, which depends on M as ω

−1/2

. Hence, there is a

substantial isotope effect on the carrier mass in polaronic and bipolaronic systems,

in contrast to the zero isotope effect in ordinary metals.

The isotope exponent in m

∗

is deﬁned as α

∗



dlnm

∗

/dlnM

,where

is the mass of the i th ion in a unit cell. Using this deﬁnition and the expression

for the polaron mass m

∗

mentioned above, one readily ﬁnds

∗

ln(m

∗

/m). (4.222)

The same isotope exponent is predicted for inter-site bipolarons, when their

mass m

∗∗

is proportional to the polaron mass (section 4.6.3). The isotope

effect on the polaron/bipolaron mass leads to an anomalous isotope effect

on the superconducting critical temperature of polaronic and bipolaronic

superconductors [82]. T

of bipolarons is the Bose–Einstein condensation

(BEC) temperature of CBG. It is approximately the Bose–Einstein condensation

temperature of ideal bosons (appendix B) as long as the Coulomb repulsion is

weak (r

1):

≈

3.31n

2/3

∗∗

(4.223)

where n

is the volume density of bipolarons. Corrections to equation (4.223),

caused by the Coulomb repulsion, are numerically small even at r

= 1 [118,119].

Hence, the isotope exponent α in T

of inter-site bipolarons is the same as α

∗∗

α ≡−

dlnT

dlnM

= α

∗∗

. (4.224)

In the crossover region from the normal polaron Fermi liquid to bipolarons, one

can apply the BCS-like expression (4.113) for T

of non-adiabatic carriers which

we write as

D exp



−g

−



λ − µ



. (4.225)

Here only g

√

M depends on M.Whenλ − µ

 Z



= e

−g

,this

expression also describes the isotope exponent in T

of inter-site bipolarons

(equation (4.223)) if their effective mass m

∗∗

∗

. In this case we can

apply equation (4.225) to the whole region of the phase diagram (ﬁgure 4.6)

including the BCS-like crossover regime and the Bose–Einstein condensation.

Differentiating equation (4.225) with respect to M yields

α = α

∗



1 −



λ − µ



. (4.226)

We see that the isotope exponent is negative in polaronic superconductors, where

λ −µ

< Z



but it is positive in bipolaronic superconductors, where λ−µ

> Z



Equation (4.225), interpolating between BCS- and BEC-type superconductivity,

allows us to understand the origin of high values of T

in comparison with the

Bipolaronic superconductivity

147

weak-coupling BCS theory (equation (2.48)). High T

originates in the polaron

narrowing of the band. The exponentially enhanced DOS of the narrow polaronic

band effectively eliminates the small exponential factor in equation (4.225). But

at a very strong e–ph coupling, T

drops again because the carriers become very

heavy. Therefore, we conclude that the highest T

is in the crossover region from

polaronic to bipolaronic superconductivity where λ − µ

≈ Z



. The polaron

half-bandwidth Z



D is normally less or about the phonon frequency ω

, so that

the maximum value of T

is estimated to be T

/3 [13]. In novel oxygen

and carbon-based superconductors (part 2), the characteristic optical phonon

frequency is about 500 to 2000 K. That is why T

is remarkably high in these

compounds.

4.7.6 Magnetic ﬁeld expulsion

The linear response function is deﬁned as

(q,ω) =



β=x,y,z

αβ

(q,ω)a

(q,ω) (4.227)

where j

(q,ω) and a

(q,ω) are the Fourier transforms of the current and of

the vector potential, respectively. To calculate the response, we need to solve

equation (4.190) with µ = 0 in the ﬁrst order with respect to A(r, t),

(r, t) =−

[∇ + i2e A(r, t)]

∗∗

(r, t)+





¯v(r −r



)|ψ

∗



, t)|

(r, t).

Using a perturbed wavefunction,

(r, t) =

√

+ φ(r, t) (4.228)

and keeping only the terms linear in A(r, t), we obtain for the Fourier transform

φ(q,ω):

ωφ(q,ω) =

∗∗

φ(q,ω)+n

¯v

{φ(q,ω)+φ

∗

(−q, −ω)}−

√

∗∗

q ·a(q,ω).

(4.229)

The solution is

φ(q,ω)+ φ

∗

(−q, −ω) =−

√

∗∗

− 

q · a(q,ω) (4.230)

φ(q,ω)− φ

∗

(−q, −ω) =−

√



− 

q · a(q,ω). (4.231)

The expectation value of the current is given by

j(r, t) =

∗∗

[ψ

∗

(r, t)∇ψ

(r, t) − ψ

(r, t)∇ψ

∗

(r, t)]−

∗∗

A(r, t).

(4.232)

148

Strong-coupling theory

Using the perturbed wavefunction, we obtain the Fourier transform of the current

j(q,ω) =

√

∗∗

q[φ(q,ω)− φ

∗

(−q, −ω)]−

∗∗

a(q,ω) (4.233)

and

αβ

(q,ω) =

∗∗



αβ



− ω

+ (q

− δ

αβ

)



(

− ω

)



. (4.234)

This response function has been split into a longitudinal K

( δ

αβ

)anda

transverse K

( (q

− δ

αβ

)) part. The longitudinal response to the ﬁeld

(D  q) is expressed in terms of the so-called external conductivity σ

(q,ω) = σ

(q,ω)D(q,ω) (4.235)

where D is the external electric ﬁeld. Using equation (4.234), we ﬁnd

(q,ω) =

iω

i

ωω

4π(ω

− 

)

. (4.236)

The conductivity sum rule (1.18) is satisﬁed as



∞

dω Re σ

(ω) =



. (4.237)

The conductivity in the transverse electromagnetic ﬁeld (D ⊥ q)isgivenby

4πλ

(4.238)

where



∗∗

16πe



1/2

. (4.239)

This expression combined with the Maxwell equation describes the Meissner–

Ochsenfeld effect in the CBG with the magnetic ﬁeld penetration depth λ

4.7.7 Charged vortex and lower critical ﬁeld

The CBG is an extreme type II superconductor, as shown later. Hence, we can

analyse a single vortex in the CBG and calculate the lower (ﬁrst) critical ﬁeld H

by solving a stationary equation for the macroscopic condensate wavefunction

[120]:



−

[∇ + 2ie A(r)]

∗∗

−µ +







|ψ



, t)|

− n

|r − r





(r, t) = 0. (4.240)

Bipolaronic superconductivity

149

Subtracting n

in the integral of equation (4.240), we explicitly take into account

the Coulomb interaction with a homogeneous charge background with the same

density as the density of charged bosons.

The integra-differential equation (4.240) is quite different from the

Ginsburg–Landau equation (1.43). While the CBG shares quantum coherence

with the BCS superconductors owing to the Bose–Einstein condensate (BEC),

the long-range (non-local) interaction leads to some peculiarities. In particular,

the vortex is charged in the CBG and the coherence length occurs just the same

as the screening radius.

Indeed, introducing dimensionless quantities f =|ψ

|/n

1/2

, ρ = r/λ(0)

and h = 2eξ(0)λ(0)∇×A for the order parameter, length and magnetic ﬁeld,

respectively, equation (4.240) and the Maxwell equations take the following form:

dρ

d f

dρ

−



dρ



− φ f = 0 (4.241)

dρ

dφ

dρ

= 1 − f

(4.242)

dρ

= h. (4.243)

The new feature compared with the GL equations of chapter 1 is the electric ﬁeld

potential determined as

φ =

2eφ





¯v(r − r



)[|ψ



− n

] (4.244)

with a new fundamental unit φ

= em

∗∗

ξ(0)

. The potential is calculated using

the Poisson equation (4.242). At T = 0, the coherence length is the same as the

screening radius,

ξ(0) = (2

1/2

∗∗

)

−1/2

(4.245)

and the London penetration depth is

λ(0) =



∗∗

16πn



1/2

. (4.246)

There are now six boundary conditions in a single-vortex problem. Four of them

are the same as in the BCS superconductor (section 1.6.3), h = dh/ρ = 0, f = 1

for ρ =∞and the ﬂux quantization condition, dh/dρ =−pf

/κρ for ρ = 0,

where p is an integer. The remaining two conditions are derived from the global

charge neutrality, φ = 0forρ =∞and

φ(0) =



∞

ρ ln(ρ)(1 − f

) dρ (4.247)

for the electric ﬁeld at the origin, ρ = 0. We note that the chemical potential is

zero at any point in the thermal equilibrium.

150

Strong-coupling theory

CBG is an extreme type II superconductor with a very large Ginsburg–

Landau parameter (κ = λ(0)/ξ(0)  1). Indeed, with the material parameters

typical for oxides, such as m

∗∗

= 10m

, n

= 10

−3

and 

= 10

,we

obtain ξ(0)  0.48 nm, λ(0)  265 nm, and the Ginsburg–Landau ratio κ  552.

Owing to a large dielectric constant, the Coulomb repulsion remains weak even

for heavy bipolarons, r

 0.46. If κ  1, equation (4.243) is reduced to the

London equation with the familiar solution h = pK

(ρ)/κ,whereK

(ρ) is the

Hankel function of imaginary argument of zero order (section 1.6.3). For the

region ρ ≤ p, where the order parameter and the electric ﬁeld differ from unity

and zero, respectively, we can use the ﬂux quantization condition to ‘integrate

out’ the magnetic ﬁeld in equation (4.241). This leaves us with two parameter-

free equations written for r = κρ:

d f

−

− φ f = 0 (4.248)

and

dφ

= 1 − f

. (4.249)

They are satisﬁed by regular solutions of the form f = c

and φ =

φ(0) + (r

/4), when r → 0. The constants c

and φ(0) are determined by

complete numerical integration of equations (4.248) and (4.249). The numerical

results for p = 1 are shown in ﬁgures 4.11 and 4.12, where c

 1.5188 and

φ(0) −1.0515.

In the region p  r < pκ, the solutions are f = 1 + (4 p

) and

φ =−p

. In this region, f differs qualitatively from the BCS order parameter,

BCS

= 1 −( p

) (see also ﬁgure 4.11). The difference is due to a local charge

redistribution caused by the magnetic ﬁeld in the CBG. Being quite different from

the BCS superconductor, where the total density of electrons remains constant

across the sample, the CBG allows for ﬂux penetration by redistributing the

density of bosons within the coherence volume. This leads to an increase of the

order parameter compared with the homogeneous case ( f = 1) in the region close

to the vortex core. Inside the core the order parameter is suppressed (ﬁgure 4.11)

as in the BCS superconductor. The resulting electric ﬁeld (ﬁgure 4.12) (together

with the magnetic ﬁeld) acts as an additional centrifugal force increasing the

steepness (c

) of the order parameter compared with the BCS superﬂuid, where

 1.1664, ﬁgure 4.11(a).

The breakdown of the local charge neutrality is due to the absence of any

equilibrium normal-state solution in the CBG below the H

(T ) line. Both

superconducting (

= 0) and normal (

= 0) solutions are allowed at any

temperature in the BCS superconductors (chapter 2). Then the system decides

which of two phases (or their mixture) is energetically favourable but the local

charge neutrality is respected. In contrast, there is no equilibrium normal-state

solution (with ψ

= 0) in CBG below the H

(T )-line because it does not respect

the density sum rule. Hence, there are no different phases to mix and the only

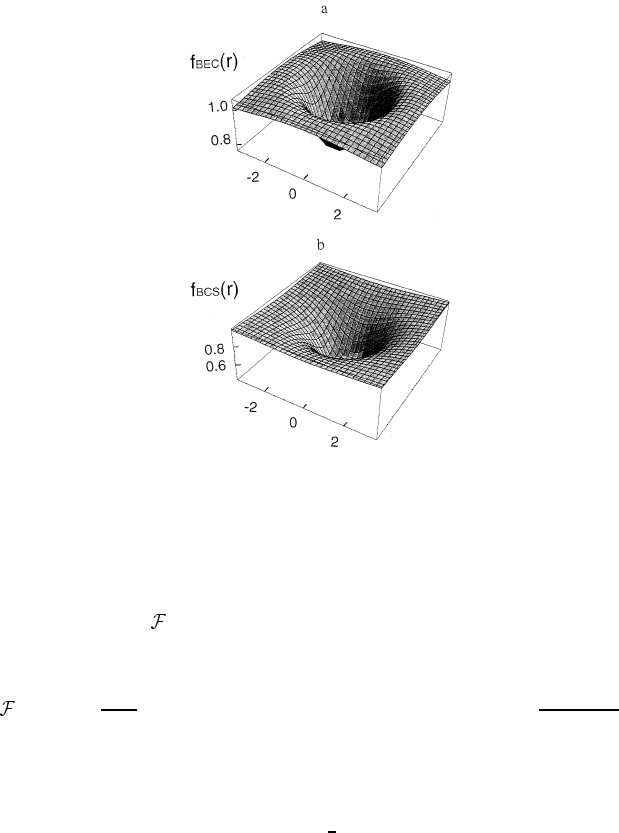
Bipolaronic superconductivity

151

Figure 4.11. Vortex core proﬁle in the charged Bose gas, f

BEC

,(a) compared with the

vortex in the BCS superconductor, f

BCS

,(b).

way to acquire a ﬂux in the thermal equilibrium is to redistribute the local density

of bosons at the expense of their Coulomb energy. This energy determines the

vortex free energy

= E

− E

, which is the difference between the energy of

the CBG with, E

, and without, E

, a magnetic ﬂux:





∗

|[∇ +2ie A(r)]ψ

(r)|

+ eφ

φ[|ψ

(r)|

− n

(∇×A)

8π



(4.250)

Using equations (4.241), (4.242) and (4.243), this can be written in dimensionless

form:

F = 2π



∞

−

φ(1 + f

)]ρ dρ. (4.251)

In the large κ limit, the main contribution comes from the region p/κ < ρ < p,

where f  1andφ −p

/(κ

). The energy is, thus, the same as that in

the BCS superconductor, F  2π p

ln(κ)/κ

(section 1.6.3). It can be seen that

the most stable solution is the formation of the vortex with one ﬂux quantum,

p = 1, and the lower critical ﬁeld is the same as in the BCS superconductor,

≈ ln κ/(2κ). However, differing from the BCS superconductor, where the

Ginsburg–Landau phenomenology is microscopically justiﬁed in the temperature

region close to T

(section 2.16), the CBG vortex structure is derived here in the

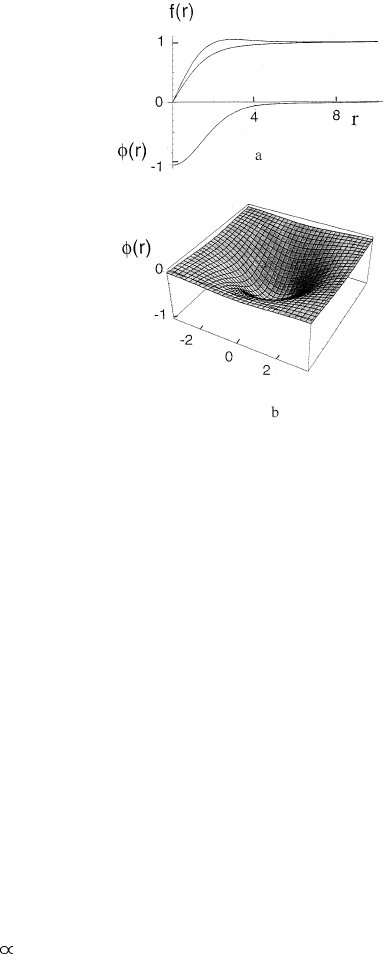
152

Strong-coupling theory

Figure 4.12. Electric ﬁeld potential φ as a function of the distance (measured in units of

ξ(0)) (lower curve) together with the CBG (upper curve) and BCS order parameters (a);

its proﬁle is shown in (b).

low-temperature region. In fact, the zero-temperature solution (ﬁgure 4.11) is

applied in a wide temperature region well below the Bose–Einstein condensation

temperature, where the depletion of the condensate remains small. The actual size

of the charged core is about 4ξ (ﬁgure 4.12).

4.7.8 Upper critical ﬁeld in the strong-coupling regime

If we ‘switch off’ the Coulomb repulsion between bosons, an ideal CBG cannot be

bose-condensed at ﬁnite temperatures in a homogeneous magnetic ﬁeld because

of one-dimensional particle motion at the lowest Landau level [7]. However, an

interacting CBG condenses in a ﬁeld lower than a certain critical value H

(T )

[121]. Collisions between bosons and/or with impurities and phonons make the

motion three dimensional, and eliminate the one-dimensional singularity of the

density of states, which prevents BEC of the ideal gas in the ﬁeld. As we show

later, the upper critical ﬁeld of the CBG differs signiﬁcantly from the H

(T ) of

BCS superconductors (section 1.6.4). It has an unusual positive curvature near T

(T ) (T

− T )

3/2

) and diverges at T → 0, if there is no localization due to

a random potential. The localization can drastically change the low-temperature

behaviour of H

(T ) (part 2).

In line with the conventional deﬁnition (section 1.6.4), H

(T ) is a ﬁeld,

where the ﬁrst non-zero solution of the linearized stationary equation for the

Bipolaronic superconductivity

153

macroscopic condensate wavefunction occurs:



−

∗∗

[∇ −2ie A(r)]

+ V

scat

(r)



(r) = µψ

(r). (4.252)

Here we include the ‘scattering’ potential V

scat

(r) caused, for example, by

impurities. Let us ﬁrst discuss non-interacting bosons, V

scat

(r) = 0. Their energy

spectrum in a homogeneous magnetic ﬁeld is (section 1.6.4)

= ω(n + 1/2) +

∗∗

(4.253)

where ω = 2eH

c2/

∗∗

and n = 0, 1, 2,...,∞. BEC occurs when the chemical

potential ‘touches’ the lowest band edge from below, i.e. µ = ω/2 (appendix B).

Hence, quite different from the GL equation (1.90), the Schr¨odinger equation

(4.252) does not allow for a direct determination of H

, In fact, it determines the

value of the chemical potential. Then using this value, the upper critical ﬁeld is

found from the density sum rule,



∞

f ()N(, H

) d = n

(4.254)

where N(, H

) is the DOS of the Hamiltonian (4.252), f () =[exp(−µ)/T −

−1

is the Bose–Einstein distribution function and E

is the lowest band edge.

For ideal bosons, we have µ = E

= ω/2and

N(, H

) =

√

2(m

∗∗

)

3/2

4π

∞



n=0

√

 − ω(n + 1/2)

. (4.255)

Substituting equation (4.255) into equation (4.254) yields

√

2(m

∗∗

)

3/2

4π



∞

1/2

exp(x /T ) − 1

= n

−˜n(T ) (4.256)

where

˜n(T ) =

√

2(m

∗∗

)

3/2

4π



∞

exp(x/T ) − 1

∞



n=1

√

x − ωn

(4.257)

is the number of bosons occupying the levels from n = 1ton =∞. This number

is practically the same as in zero ﬁeld, ˜n(T ) = n

(T /T

)

3/2

(see equation (B.61)),

if ω  T

. In contrast, the number of bosons on the lowest level, n = 0, is given

by a divergent integral on the left-hand side of equation (4.256). Hence the only

solution to equation (4.256) is H

(T ) = 0.

The scattering of bosons effectively removes the one-dimensional singularity

in N

(, H

) ω( − ω/2)

−1/2

leading to a ﬁnite DOS near the bottom of the

lowest level,

(, H

) ∝

√



)

. (4.258)

154

Strong-coupling theory

Using the Fermi–Dirac golden rule, the collision broadening of the lowest level



) is proportional to the same DOS:



) ∝ N

(, H

) (4.259)

so that 

scales with the ﬁeld as 

) H

2/3

. Then the number of bosons

at the lowest level is estimated to be

√

2(m

∗∗

)

3/2

4π



∞



1/2

exp(x/T ) − 1

2/3

(4.260)

as long as T  

. Here we apply the one-dimensional DOS but cut the integral

at 

from below. Finally we arrive at

(T ) = H

−1

− t

1/2

)

3/2

(4.261)

where t = T/T

and H

is a temperature-independent constant. The scaling

constant, H

, depends on the scattering mechanism. If we write H



/(2πξ

), then the characteristic length is

≈





1/4

(4.262)

where l is the zero-ﬁeld mean-free path of low-energy bosons. The upper critical

ﬁeld has a nonlinear behaviour:

(T ) ∝ (T

− T )

3/2

in the vicinity of T

and diverges at low temperatures as

(T ) T

−3/2

These simple scaling arguments are fully conﬁrmed by DOS calculations

with impurity [121] and boson–boson [122] scattering. For impurities, the energy

spectrum of the Hamiltonian (4.252) consists of discrete levels (i.e. localized

states) and a continuous spectrum (extended states). The density of extended

states

N (, H

) and their lowest energy E

(the so-called mobility edge, where

N (E

, H

) = 0) can be found, if the electron self-energy () is known. We

calculate () in the non-crossing approximation of section 3.3 considering the

impurity scattering as the elastic limit of the phonon scattering:



() =





νν



 − 



− 



()

. (4.263)

To obtain analytical results, we choose the matrix elements of the scattering

potential as V

νν



= V δ



.Hereν ≡ (n, k

, k

) are the quantum numbers of

a charge particle in the magnetic ﬁeld. Then the DOS is found to be

N (, H

) =

π V



Im 

(). (4.264)

Bipolaronic superconductivity

155

Integrating over k

in equation (4.263) yields a cubic algebraic equation for the

self-energy 

() of the nth level:



() =

2π



∞

−∞

 − ω(n + 1/2) − k

/(2m

∗∗

) − 

()

√

∗∗

√

 − ω(n + 1/2) − 

()

. (4.265)

Solving this equation, we obtain

N (, H ) =

4π



∗∗



∞



n=0











˜



˜





1/3

−





˜

−



˜





1/3







(4.266)

and the mobility edge

−

3

2/3

. (4.267)

Here





√

∗∗



2/3

is the collision broadening of levels and ˜

=[ − ω(n + 1/2]/

With this DOS in the sum rule (equation (4.254)), we obtain the same H

(T )

for T  

as through the scaling, equation (4.261), and

≈ 0.8





1/4

. (4.268)

The zero-ﬁeld mean free path l is expressed via microscopic parameters as

l = π/(Vm

∗∗

)

−2

. The ‘coherence’ length ξ

of the CBG (equation (4.268))

depends on the mean free path l and the inter-particle distance n

−1/3

. It has little

to do with the size of the bipolaron and could be as large as the coherence length

of weak-coupling BCS superconductors.

Thus H

(T ) of strongly-coupled superconductors has a ‘3/2’ curvature

near T

which differs from the linear weak-coupling H

(T ) of section 1.6

(ﬁgure 4.13). The curvature is a universal feature of the CBG, which does not

depend on a particular scattering mechanism and on any approximations. Another

interesting feature of strongly-coupled superconductors is a breakdown of the

Pauli paramagnetic limit given by H

 1.84T

in the weak-coupling theory

(section 1.6.4). The H

(T ) of bipolarons exceeds this limit because the singlet