Алексеев В.В. Физическое и математическое моделирование экосистем

Подождите немного. Документ загружается.

тен

(см. п. 1.6),

совпадающей

выражением (2.9), предложенным

Моно.

Зависимость Моно оказывается

ряде случаев справедливой

при

лимитировании пищей крупных организмов, например

рыб.

Так,

В. С.

Ивлевым

[70] при

изучении питания

рыб

эксперимен-

тально было получено соотношение

между

рационом (скоростью

питания)

г и

концентрацией пищи

среде

где

R —

максимальный рацион;

k —

коэффициент пропорциональ-

ности.

общем

случае

интегрирование уравнения

дает

зависи-

мость

= Я

(1-ехр

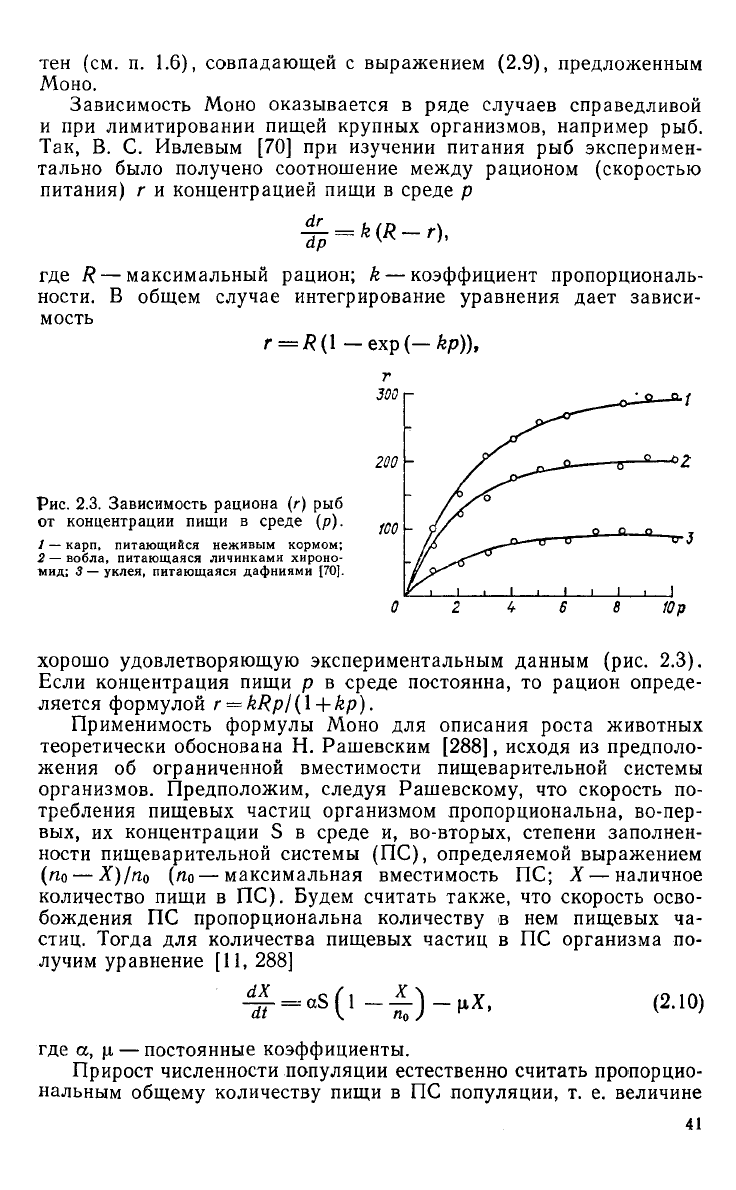
Рис.

2.3. Зависимость рациона (г) рыб

от концентрации пищи в

среде

(р).

—

карп, питающийся неживым кормом;

—

вобла, питающаяся личинками хироно-

мид;

3 —

уклея, питающаяся дафниями

[70].

Ь 6 в Юр

хорошо удовлетворяющую экспериментальным данным

(рис. 2.3).

Если концентрация пищи

р в

среде постоянна,

то

рацион опреде-

ляется формулой

r =

kRp/(l+kp).

Применимость формулы Моно

для

описания роста животных

теоретически обоснована

Н.

Рашевским [288], исходя

из

предполо-

жения

об

ограниченной вместимости пищеварительной системы

организмов. Предположим, следуя Рашевскому,

что

скорость

по-

требления пищевых частиц организмом пропорциональна, во-пер-

вых,

их

концентрации

S в

среде

и,

во-вторых, степени заполнен-

ности пищеварительной системы

(ПС),

определяемой выражением

(па

— Х)/по («о —

максимальная вместимость

ПС; X —

наличное

количество пищи

в ПС).

Будем считать также,

что

скорость осво-

бождения

ПС

пропорциональна количеству

в нем

пищевых

ча-

стиц. Тогда

для

количества пищевых частиц

в ПС

организма

по-

лучим уравнение

[11, 288]

—7^

= 0:8(1 ) — аХ,

(2.10)

По

)

где

а, |л —

постоянные коэффициенты.

Прирост численности популяции естественно считать пропорцио-

нальным общему количеству пищи

в ПС

популяции,

т. е.

величине

XN, где N— численность популяции. Считая, что смертность в по-

пуляции пропорциональна численности, получим уравнение

-jp = yXN — eN,

(2.11)

где е — коэффициент естественной смертности; у — коэффициент

усвоения пищи.

Время, в течение которого происходят значительные изменения

численности популяции, как правило, значительно больше, чем

время достижения стационарной заполненности ПС организмов при

данной концентрации пищи. Поэтому, используя теорему

А. Н. Тихонова, можно считать, что питание особей происходит

в стационарном режиме и

dX/dt

— O.

Отсюда

у- поХ

(2.12)

где Hmax=Yrto; K =

/a.

Уравнение

(2.12)

с точностью до обозначений совпадает с форму-

лой Моно (2.9) при

учете

в (2.9) потерь, связанных с отмиранием,

дыханием, выделением метаболитов.

Широкая

применимость формулы Моно для описания роста

популяций самых различных организмов привела к

тому,

что урав-

нения

роста, основанные на этой формуле, стали базовыми в мате-

матической экологии и используются с различными модификаци-

ями

в большинстве теоретических работ, посвященных исследова-

нию взаимодействия организмов со средой обитания, а также пи-

щевым взаимодействиям

между

организмами разных трофических

уровней.

Использование формулы Моно сыграло важную роль и в раз-

витии кинетической микробиологии, поскольку появилась возмож-

ность оценки условий среды и сравнения свойств видов по экспе-

риментально определяемым кинетическим параметрам К и

|Я

ах-

Экспериментальные значения кинетических параметров К и

Цтах получены для ряда видов микроорганизмов при лимитирова-

нии

их роста различными элементами питания [178, 188]. На

рис.

2.4 приведены кривые насыщения, экспериментально получен-

ные для диатомовой водоросли

Diatoma

elongatum

при лимитиро-

вании

ее фосфатами и силикатами, а также соответствующие кри-

вые обратных величин, позволяющих определять К и ц

ах (гра-

фик

Лайнуивера—Берка) [218].

Следует

отметить, что кинетиче-

ские параметры К и Umax отражают поведение популяции при

лимитировании отдельным компонентом питания, но не характе-

ризуют максимально возможной продуктивности вида. Так, для

водоросли

Diatoma

elongatum

(см. рис. 2.4) максимальные скоро-

сти роста, вычисленные по формуле Моно, оказываются различ-

0,5

0,3

0,1

30\IM

0 1

ЦМ

f/S

Рис.

2.4.

Удельная

скорость размножения водоросли

Diatoma

elongatum

как

функция

содержания в

среде

фосфатов (о) и силикатов (б) и график Лай-

нуивера—Берка для определения параметров уравнения Моно (в) [218].

ными

и равными для фосфата Цтах(Р) =0,7; для силиката

Mmax(Si) = 1,23

сут"

Значения К и

(Лтах

зависят также от кон-

кретной

химической формы лимитирующего компонента питания.

Например,

для диатомеи

Sceletonema

costatum

константы полуна-

сыщения

при лимитировании нитратным и аммонийным азотом

резко

отличаются и составляют соответственно 7 и 50 мкг/л (при

пересчете на азот) [178]. В опытах Моно по росту культуры

В.

coli

на различных источниках углеродного питания также были

зафиксированы

различия как в максимальных скоростях роста,

так

и в константах полунасыщения, что хорошо видно из рис. 2.2.

В общем

случае

необходимо определение кинетических харак-

теристик

для каждой из основных форм лимитирующего элемента

питания.

2.4.

Замкнутая

система

хемостат

Используя

«принцип минимума» Либиха и формулу Моно, ди-

намику

биомассы М изолированной популяции можно описать

уравнением

^ ^-,

(2.13)

где е—коэффициент смертности и метаболических потерь.

Уравнение роста

(2.13)

содержит две переменные — биомассу

концентрацию в среде лимитирующего ресурса питания S. Оче-

видно,

что для замыкания системы уравнение

(2.13)

необходимо

дополнить

уравнением, описывающим динамику лимитирующего

биогена.

В данной книге в основном

будут

рассматриваться два типа

моделей — экосистемы с замкнутым круговоротом лимитирующего

биогенного

элемента, а также экосистемы с постоянной скоростью

протока

питательных веществ через систему, так называемые про-

точные (хемостатные) системы.

В системе с замкнутым круговоротом лимитирующего элемента

(система с консервативным ресурсом) величина S определяется

из

уравнения сохранения общего запаса лимитирующего элемента

системе. В простейшем

случае

динамика одной популяции в зам-

кнутой системе описывается уравнениями

(2.13)

M + S = M

(2.14)

где М — биомасса популяции, выраженная в единицах содержания

лимитирующего элемента питания; S — концентрация этого эле-

мента в среде; М

— общее содержание элемента в системе.

Использование

алгебраического закона сохранения вещества

математических моделях экосистем позволяет записывать замк-

нутые

системы уравнений и проводить достаточно глубокий ана-

лиз

возможных динамических режимов. В нашей стране широкие

теоретические исследования экосистем с замкнутым круговоротом

лимитирующих элементов питания проводятся в Московском го-

сударственном университете с начала

1970-х

годов

В. В. Алексее-

вым и его учениками [10, 11, 62]. Возможности конструктивного

анализа моделей экосистем с консервативным ресурсом

будут

продемонстрированы в последующих

главах

книги.

Обсудим

вопрос, насколько реалистично использование урав-

нения

сохранения элемента для описания экосистемы. Как было

подробно рассмотрено в гл. 1, само существование и функциони-

рование природной экосистемы построено по принципу замыкания

круговорота биогенных элементов, поэтому в среднем в длительно

существующей

экосистеме содержание

всех

элементов поддержи-

вается на постоянном уровне. Временная задержка в разложении

органических остатков до минеральных компонент в естественных

экосистемах компенсируется наличием

двух

фондов элемента —

обменного и запасного (буферного). Буферный фонд находится

равновесии с обменным, поглощая непереработанные

отходы

возвращая в

среду

эквивалентное количество минеральных компо-

нент

из ранее поступивших органических остатков. При этом

обменном фонде элемента количество его остается приблизи-

тельно постоянным. Примерами запасных фондов являются дон-

ные

отложения в

водоемах,

листовой опад в

лесах

и т. д. В ис-

кусственных экосистемах замкнутая циркуляция вещества может

осуществляться

путем

принудительной быстрой регенерации ре-

сурса,

например, химическим

путем

(в системах космического жиз-

необеспечения) .

Нетрудно показать, что система уравнений (2.13),

(2.14)

дает

кривую роста популяции, практически совпадающую с логистиче-

ской

кривой. Система имеет два стационарных состояния, причем

нетривиальное определяется формулами

S =

-J^ZT=M,K

;

M = M

-M

1KP

(2.15)

устойчиво при Ms > Mi

p. Если запас элемента в системе

меньше Mi

то

устойчивым становится нулевое положение

рав-

новесия,

популяция вымирает.

Начиная

1950-х

годов

экспериментальных исследованиях

микробиологической промышленности широкое распространение

получило культивирование микроорганизмов

системах

постоян-

ным

протоком

—

хемостатах.

Хемостат

был

предложен

в 1950 г.

Ж.

Моно

позволял избавиться

от

обычного

для

непроточного

способа культивирования чрезмерного накопления продуктов мета-

болизма

среде [259]. Принципиальная схема хемостата пока-

зана

на рис. 2.5.

Теория хемостата

была разработана

работах Моно,

Новика,

Сцилларда

и др.

[259,

269,

241]. Хемостаты оказались чрезвы-

чайно

удобными

как для

экспери-

ментальных,

так и для

теоретиче-

ских исследований процессов

эко-

системах. Популяции микроорганиз-

мов

хемостатах

имеют высокие

численности,

что

позволяет приме-

нять

аппарат дифференциальных

уравнений

для их

описания. Кроме

того,

большинстве случаев можно

пренебрегать возрастной структурой

популяций,

эффектами запаздыва-

ния,

пространственное распределе-

ние

считать однородным.

Все эти

Питатель-

ный

растйор

___ О п

— гг

Культиватор"*-

Рис.

2.5.

Принципиальная

схема

хемостата-

аппарата

для

непрерывного культивирова-

ния

микроорганизмов [259].

-_5трабо~_

тинная

'жидкость-

факторы,

также возможность достаточно точного воспроизве-

дения

результатов экспериментов позволили построить достаточно

надежный

экспериментально проверенный математический

ап-

парат

для

описания экосистем

проточных условиях.

Динамика

биомассы популяции

концентрации лимити-

рующего элемента

среде

для

проточной системы описывается

дифференциальными

уравнениями

= D(S

-S)-n

SM/(K-

(2.16)

где

D —

скорость протока,

S° —

концентрация лимитирующего био-

гена

на

входе

системы.

На

основании закона сохранения вещества, протекающего

че-

рез систему, нетрудно видеть,

что в

равновесном режиме суммар-

ное

количество свободного

связанного

организмах химического

элемента должно быть равно его концентрации в поступающем на

вход

системы потоке биогенного элемента. Действительно, сложив

уравнения

(2.16)

и проинтегрировав полученную

сумму,

получим

соотношение

S (t) = S° — М + С ехр (- Dt),

(2.17)

S(0)-S°

+ M(0),

где S(0), M(0)—соответственно концентрация лимитирующего

элемента и биомасса популяции в начальный момент времени.

После

затухания экспоненциального члена выражение

(2.17)

полностью совпадает с уравнением сохранения

(2.14)

при М

S°. Система уравнений

(2.16)

имеет состояние нетривиального

равновесия,

стационарные значения переменных выражаются фор-

мулами

(2.15)

при e = D. Таким образом, проточная система

имеет те же состояния равновесия, что и замкнутая система с за-

пасом лимитирующего элемента питания Mj3 = S°.

математической точки зрения исследование замкнутых эко-

систем проще, поэтому моделирование, как правило,

будет

прово-

диться на примерах замкнутых систем с

учетом

того, что разли-

чия

в поведении замкнутых и проточных систем

могут

проявляться

лишь

в неравновесных режимах.

2.5.

«Принцип минимума» и

смена

факторов,

лимитирующих

рост популяции

Использование

в математических моделях зависимости скоро-

сти роста популяции как функции одного элемента питания (x(S)

допустимо только для систем с установившимся характером лими-

тирования.

Между тем, смена факторов лимитирования встреча-

ется повсеместно и представляет как теоретический, так и важ-

ный

практический интерес в микробиологическом производстве,

аквакультуре, в исследованиях изменений экосистем при антропо-

генном воздействии.

Наиболее четко смену лимитирования можно проследить в хе-

мостате, используя так называемый эффект аутостабилизации ли-

митирующего фактора [59]. Возвращаясь к формулам (2.15),

легко заметить, что при выращивании популяции в'хемостате, кон-

центрация

лимитирующего субстрата устанавливается на посто-

янном

уровне (S = const) независимо от его концентрации на

входе

хемостата (S

). Биомасса же популяции прямо пропорциональна

поступлению субстрата на

вход

хемостата: M=S° — S; экспери-

ментальные данные, подтверждающие это явление, представлены

на

рис. 2.6.

Смена

лимитирующих факторов в процессе роста популяции

наглядно продемонстрирована в работе [109] на примере наблю-

дений

за культурой дрожжей

Candida

tropicalis,

результаты ко-

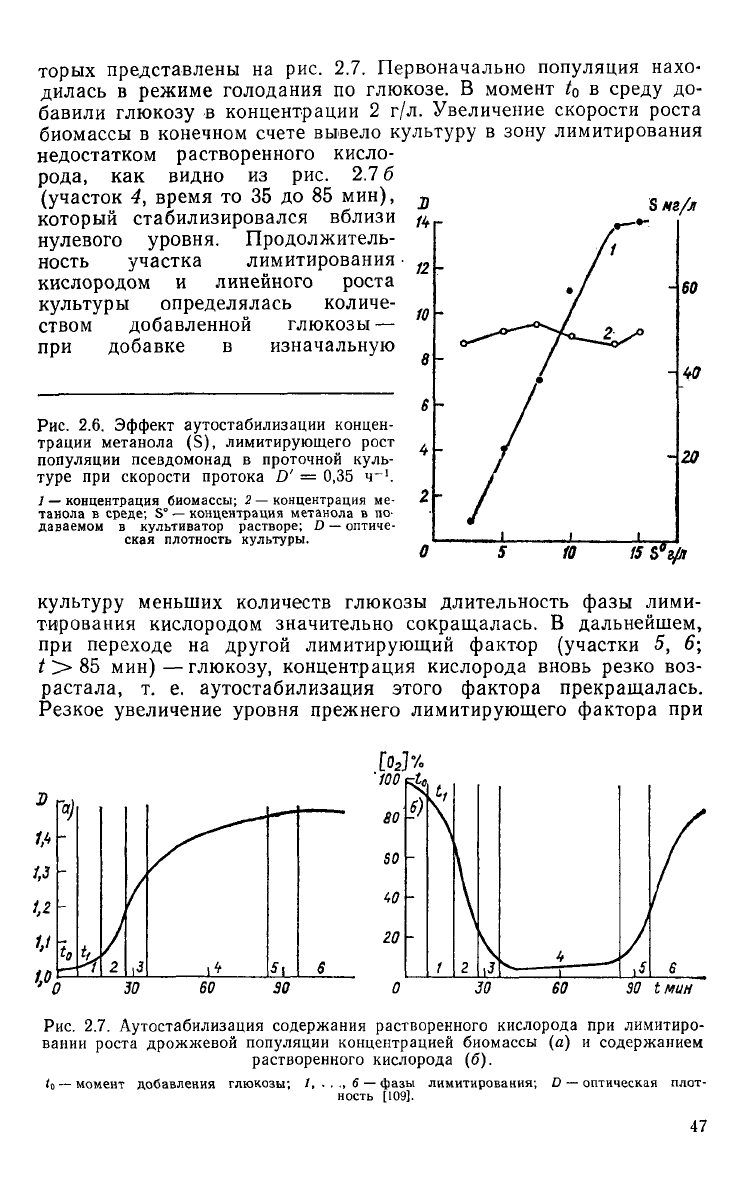
торых представлены на рис. 2.7. Первоначально популяция нахо-

дилась в режиме голодания по глюкозе. В момент /

среду

до-

бавили глюкозу в концентрации 2 г/л. Увеличение скорости роста

биомассы в конечном счете вывело

культуру

в зону лимитирования

недостатком растворенного кисло-

рода, как видно из рис. 2.7 6

(участок 4, время то 35 до 85 мин),

который

стабилизировался вблизи

нулевого уровня. Продолжитель-

ность участка лимитирования

кислородом и линейного роста

культуры определялась количе-

ством добавленной глюкозы —

при

добавке в изначальную

Рис.

2.6. Эффект аутостабилизации концен-

трации метанола (S), лимитирующего рост

популяции псевдомонад в проточной куль-

туре

при скорости протока D' = 0,35 ч~

—

концентрация биомассы;

2 —

концентрация

ме-

танола

среде;

S° —

концентрация метанола

в по-

даваемом

культиватор растворе;

D —

оптиче-

ская

плотность

культуры.

Ънг/л

№

культуру

меньших количеств глюкозы длительность фазы лими-

тирования

кислородом значительно сокращалась. В дальнейшем,

при

переходе на

другой

лимитирующий фактор (участки 5, 6;

t > 85 мин)—глюкозу, концентрация кислорода вновь резко воз-

растала, т. е. аутостабилизация этого фактора прекращалась.

Резкое

увеличение уровня прежнего лимитирующего фактора при

100

30 30 60

tMUH

Рис.

2.7. Аутостабилизация содержания растворенного кислорода при лимитиро-

вании

роста дрожжевой популяции концентрацией биомассы (а) и содержанием

растворенного кислорода (б).

—

момент добавления глюкозы;

1 6 —

фазы лимитирования;

D —

оптическая плот-

ность [109].

его смене другим является общим свойством как периодических

(непроточных), так и хемостатных культур.

Существует несколько различных подходов к теоретическому

описанию

механизма смены факторов, лимитирующих рост попу-

ляции.

Наиболее распространенными являются модели с жестким

переключением, когда предполагается строгое выполнение поло-

жения

о контроле роста только одним элементом питания в любой

момент времени. Среди моделей этого типа можно отметить два

варианта определения момента смены лимитирования.

Первый

вариант основан на представлениях об

«узком

месте»

метаболизма: лимитирующим считается элемент питания, даю-

-Г

Г*

s,,s

Рис.

2.8. Кривые

Моно

ц< = VmiSil(Ki+Si) для удельной скорости роста

jii(t = 1; 2) при лимитировании роста популяции субстратами Si, S

(а) и изо-

линии

скорости роста для случая жесткого переключения по лимитированию (б)

[315].

щий

наименьшую скорость роста популяции. Например, для мо-

дели Моно смена лимитирующего элемента питания Si на S

за-

писывается следующим образом [2, 3, 72]:

Hm,

»*л

. о , если -тг-

ftl + bi Ai

Si Л'г + S

(2.18)

если

Ai -f-

Графическое определение лимитирующего элемента в этом ва-

рианте представлено на рис. 2.8 а. Из математической формы

функций

м-(Si) и ц(5г)

следует,

что смена лимитирования может

происходить только при неравенстве максимальных скоростей ро-

ста:

\Ут

{

Ф\Ьт

На рис. 2.86 представлено семейство изолиний

скорости роста популяции, потребляющей два потенциально лими-

тирующих элемента питания Si и S

, для модели (2.18).

Во втором варианте для описания смены лимитирования ис-

пользуется способ, предложенный Либихом: лимитирующим явля-

ется элемент питания, для которого отношение «концентрация

в среде/концентрация в организме» оказывается наименьшим по

сравнению с другими незаменимыми компонентами питания.

Смена лимитирования в этом варианте записывается следующим

образом:

Hm, Si S, S

если

(2.19)

если

где cti,

0&2

— удельное содержание первого и второго элементов

в организмах популяции соответственно.

Различия в описанных способах

(2.18)

(2.19)

определения

лимитирующих элементов удобно показать, рассмотрев динамику

популяции в замкнутой экосистеме при наличии

двух

потенциально

лимитирующих элементов питания.

Система уравнений модели с переключением в форме

(2.18)

(по

скорости роста) имеет вид

dM. .. , . .

= M(-e + n),

(2.20)

Si-

где a

0С2 определяют содержание химических элементов в био-

массе М.

Уравнения модели с переключением в форме

(2.19)

(по соотно-

шению элементов) имеют вид [9, 24]

(2.21)

S. + a.M-S?,

+ a

M = S

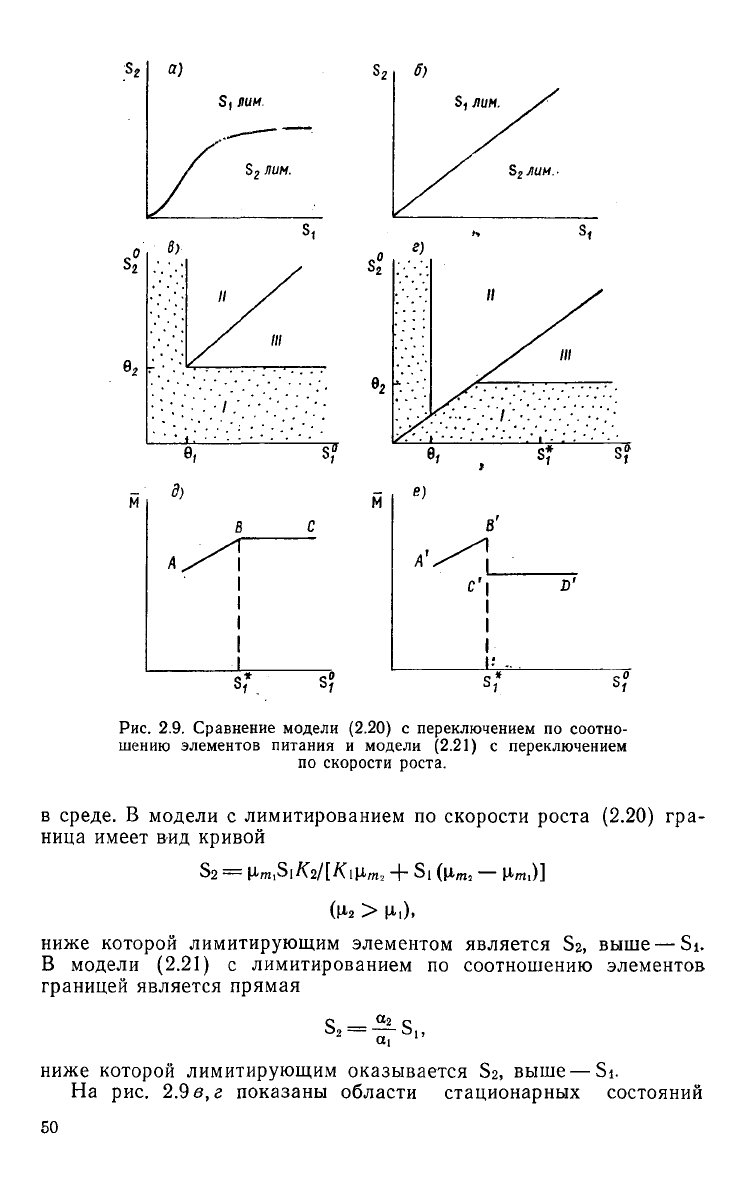
Результаты исследования динамики и стационарных состояний

моделей

(2.20)

(2.21)

представлены на рис. 2.9 а, в,д и

2.9 6, г, д соответственно. На рис. 2.9 а, б показаны линии смены

лимитирования на плоскости концентраций (Si, S2) элементов

4 Заказ № 57 49

а)

ним

HUM.

в)

II /

/ '"

9, г

пим. •

г)

с'\

о*

!•• -

Рис.

2.9. Сравнение модели

(2.20)

с переключением по соотно-

шению элементов питания и модели

(2.21)

с переключением

по

скорости роста.

среде. В модели с лимитированием по скорости роста

(2.20)

гра-

ница

имеет вид кривой

, + Si ([im, —

ниже которой лимитирующим элементом является S2, выше — Si.

В модели

(2.21)

с лимитированием по соотношению элементов

границей

является прямая

«2

—

ниже которой лимитирующим оказывается S2, выше — Si.

На

рис. 2.9 в, г показаны области стационарных состояний