Accardi L., Freudenberg W., Obya M. (Eds.) Quantum Bio-informatics IV: From Quantum Information to Bio-informatics
Подождите немного. Документ загружается.


360
conductivity
can
be
found as
-e
2
!'i
00
1 J
jPrna
x 2
o
f(w) R A
O'xx
=
4m
2
L L
27f
dw
dp
P
~GMex(p,W)GMa(P,W)
0:
M=O
-Prnax
x
{I
+
~ReAII(p,w)}
(18)
where f(w) =
(l+exp(,8hw))-I,
GR (G
A
)
is
the
retarded
(advanced) Green
function,
and
An is
the
vertex
function.
The
theories so far proposed con-
sider
the
effects
ofthe
millimeterwave
radiation
on
the
2DES only. However,
if
there
is
an
electron reservoir,
the
effects
of
the
radiation
on
the
electrons
in
the
reservoir should also
be
taken
into account.
Since
the
amount
of
energy
that
an
excited electron
can
receive from
millimeterwave
radiation
is !'iv,
the
condition
under
which
the
electron
can
join
the
2DES should be hw
e
/ 2 + E
res
< !'iv.
This
condition
can
also
be
written
as B < (2mc/!'ie)(!'iv - Eres)
==
Be. As
the
chemical
potential
is
the
minimum
free energy
to
add
an
electron
to
the
system,
the
emergence
of
such a process
may
be
described by
introducing
another
singularity in
the
retarded
Green function
at
!'iv.
This
singularity of
the
Green function
may
be
expressed as
an
effective chemical potential.
Then
the
conductivity
formula
(18)
yields
I4
e
2
A e
2
A
O'xx
= -
{WIBI
+ W
2
B
2
+
~B}
==
-WON
m m
(19)
when
the
radiation
is on,
and
e
2
A e
2
A
O'xx
= - {W2 +
~B}
==
-WOFF
m m
(20)
when
the
radiation
is off. Here
~
==
(-e/47f
2
mcA)
LM
AO
is assumed
to
be
a
constant,
and
Wi'S
are
given
as
Wi
= L f
,8
hw
e (21)
ex
M = O
{1
+
e(3(c
M
,,-TJ;l}
{I
+
e-(3(C
M
,,-TJil} .
In
the
measurement
by Zudov
et
al.
ll
the
current
Ix is
measured
by con-
trolling
the
electric field Ex, while
the
current
Iy as well as
the
external
electric field Ey
are
kept zero. Therefore,
the
resistivity Rxx observed in
their
measurement
should correspond
to
1/0'
xx
in
this
theory.
The
resistiv-
ity
corresponding
to
Rxx
in
RefY
is given as
(22)

361
The
theoretical
pattern
shows excellent agreement
with
the
experimental
curve.
The
B-dependence
of
the
oscillatory
patterns
of
the
millimeterwave
induced magnetoresistance oscillations observed by Zudov
et
al.
ll
is almost
perfectly
reproduced
from
our
theoretical model based
on
the
FLH
and
the
ERH,
including
its
immunity
to
the
polarization
of
the
radiation
field in
perfect accordance
with
the
experimental
observation by
Smet
et
al.
13.
5.
Concluding
Remarks
We have shown
that
the
electron reservoir model
can
perfectly explain
the
three
prominent
phenomena
in semiconductor 2DES.
Although
experimen-
tal
identification of
the
microscopic mechanism
of
the
electron reservoir
still needs
to
be
carried
out,
there
seems
to
be
no
doubt
that
the
electron
reservoir should exist
in
those systems.
References
1.
G. A.
Baraff
and
D. C. Tsui,
Phys.
Rev. B
24,
2274 (1981).
2.
T.
Toyoda, V.
Gudmundsson,
and
Y.
Takahashi,
Phys.
Lett.
102A,
130
(1984)
3.
T.
Toyoda
, V.
Gudmundsson,
and
Y.
Takahashi,
Physica
132A,
164 (1985).
4.
K.
von
Klitzin, G.
Dorda,
and
M.
Pepper
,
Phys.
Rev
.
Lett.
45,
494 (1980).
5.
T.
Toyoda,
Phys
.
Rev
. A
39,
2659(1989)
6.
S.
Holland
, Ch. Heyn, D.
Heitmann,
E.
Batke,
R.
Hey,
K.
J.
Friedl
an
d,
and
C.-M. Hu,
Phys.
Rev.
Lett.
93,
186804 (2004).
7.
T.
Toyoda, N. Hiraiwa,
T.
Fukuda,
and
H. Koizumi,
Phys.
Rev.
Lett.
100,
036802 (2008).
8.
T.
Toyoda, V.
Gudmundsson
,
and
Y.
Takahashi,
Physica
132A
, 164 (1985).
9.
M. P. Greene, H. J. Lee,
J.
J.
Quinn,
and
S.
Rodriguez,
Phys.
Rev.
177,
1019 (1969).
10. N. Hiraiwa
and
T.
Toyoda,
in
preparation.
11. M.A. Zudov, D.R.
Du,
J.A.
Simmons,
and
J.L. Reno,
Phys.
Rev. B
64,
201311 (2001).
12.
R.
G. Mani,
J.
H.
Sm
et,
K. von Klitzing, V.
Narayanamurti,
W.
B.
Johnson,
and
V. Umansky,
Nature
420,646
(2002).
13.
J.
H. Smet , B. Gorshunov, C.
Jiang,
L. Pfeiffer,
K.
West, V. Umansky, M.
Dressel,
R.
Meisels,
F.
Kuchar,
and
K. von
Klitzing
,
Phys.
Rev.
Lett.
95,
116804 (2005).
14.
T.
Toyoda,
Modern
Physics
Letter
s B,
24
, 1923 (2010).

This page intentionally left blankThis page intentionally left blank

Quantum
Bio-Informatics
IV
eds. L.
Accardi,
W.
Freudenberg
and
M.
Ohya
© 2011
World
Scientific
Publi
sh
ing
Co.
(pp.
363-372)
ON
THE
CORRESPONDENCE
BETWEEN
NEWTONIAN
AND
FUNCTIONAL
MECHANICS
E.V.
PISKOVSKIY,
LV.
VOLOVICH
Moscow
Institute
of
Physics
and
Technology
Institustkiy
lane 9,
141700
Dolgoprudny,
Moscow
Region
,
Russia
email:
piskovskiy@mi.ms.ru
Steklov
Mathemati
cal
Institute
Gubkin
St.8,
119991 Moscow,
Russia
email:
volovich
@mi.
ms.ru
The
world
view
underl
y
ing
traditional
science is
based
on reductionism
and
deter-
minism
when
there
is
an
empty
space
(vacuum)
and
material
points
which
move
along
the
Newtonian
trajectories.
This
approach
may
be
called
"mechanistic"
or
"
Newtonian"
.
Quantum
mechanics,
in
its
Copenhagen
int
erp
retation,
also
adopts
this
world
view.
Howev
er
this
world
view
is
not
satisfactory
by
at
least
two
rea-
sons.
First,
there
is
uncertainty
in
the
derivation
of
the
position
and
velocity
of
the
material
point
and
second,
it
can
not
so
lve
the
time
irreversibility
problem.
Moreover,
the
Newtonian
approach
is
not
well
suited
for
applications
of
mathemat-
ics
and
physics
to
life science.
Recently
a
new
approach
to
classical
mechanics
was
proposed
in
which
the
basic
notion
is
not
th
e
trajectory
but
a
probability
distri-
bution.
In
this
functional
mechanics
approach
one
deals
with
the
mean
trajectories
and
one
has
corrections
to
the
Newtonian
equa
tion
of
motion.
In
this
note
we
consider
correspondence
between
the
Newtonian
trajectories
for
an
anharmonic
oscillator
and
the
averaged
trajectories
in
the
functional
m
echan
ics
and
compute
the
depend
ence
of
the
characteristic
time
from
the
dispersion.
1.
Introduction
Classical mechanics, as first formulated
by
Newton
and
further
developed
by
others,
was seen,
until
the
early
20th
century, as
the
foundation
for
science as a whole.
Other
disciplines, such as physics, biology,
or
economics,
did
accept
a general mechanistic
or
Newtonian
approach
and
world view.
Even
quantum
mechanics is
based
on
the
classical
deterministic
Newtonian
mechanics, according
to
the
Copenhagen
interpretation.
The
basic principle
behind
Newtonian
science is reductionism:
to
un-
derstand
any
complex
phenomenon,
you need
to
reduc
e
it
to
its individual
components.
The
smallest
possible
parts
are
called
atoms
or
"elementary
363

364
particles".
The
only
property
that
fundamentally
distinguishes particles is
their
position
in
space
and
velocities.
If
you know
the
initial positions
and
velocities
of
the
particles
constituting
a
system
together
with
the
forces
acting
on
those
particles,
then
you
can
in principle
predict
the
further
evo-
lution
of
the
system
with
complete
certainty
and
accuracy.
The
evolution
will
be
regular, reversible
and
predictable. Such categories as life,
mind,
or
organization
are
to
be
seen as
particular
arrangements
of
particles in space
and
time.
However
the
Newtonian
world view is
not
satisfactory
by
at
least two
reasons.
First,
there
is
uncertainty
in
the
derivation
of
the
position
and
ve-
locity
of
the
material
point.
Second,
it
can
not
solve
the
time
irreversibility
problem, see
1;
for a discussion
of
the
irreversibility
problem
see
2.
More-
over,
the
Newtonian
approach
is
not
well
suited
for
applications
of
math-
ematics
and
physics
to
life science.
Recently
a new
approach
to
classical
mechanics was
proposed
in which
the
basic
notion
is
not
the
trajectory
but
a
probability
distribution.
In
this
functional mechanics
approach
1,
see also
3,4,5,6
,
7,
one deals
with
the
mean
trajectories
and
one
has
corrections
to
the
Newtonian
equation
of
motion.
Emphasize
that
the
exact
derivation
of
the
coordinate
and
momentum
can
not
be
done,
not
only
in
quantum
mechanics, where
there
is
the
Heisen-
berg
uncertainty
relation,
but
also in classical mechanics. Always
there
are
some errors in
setting
the
coordinates
and
momenta.
There
are
classical
uncertainty
relations
1:
!:,.q
>
0,
!:,.p>
0,
i.e.
the
uncertainty
(errors
of
observation) in
the
determination
of
coordi-
nate
and
momentum
is always positive (non zero).
The
concept
of
arbitrary
real
numbers,
given
by
the
infinite decimal series, is a
mathematical
ideal-
ization, such
numbers
can
not
be
measured
in
the
experiment.
In
this
note
we
consider correspondence
between
the
Newtonian
tra-
jectories for
an
anharmonic
oscillator
and
the
averaged
trajectories
in
the
functional mechanics
and
compute
the
dependence
of
the
characteristic
time
from
the
dispersion. We
are
motivated
by
the
consideration
of
the
quantum
classical correspondence for
the
baker's
map
performed
by
Inoue,
Ohya
and
one
of
the
present
authors
8.
Note
that
the
conventional widely used concept
of
the
microscopic
state
of
the
system
at
some
moment
in
time
as
the
point
in
phase
space, as well
as
the
notion
of
trajectory
and
the
microscopic
equations
of
motion
have
no
direct
physical meaning, since
arbitrary
real
numbers
not
observable

365
(observable physical
quantities
are
only
presented
by
rational
numbers).
The
fundamental
equation
of
the
microscopic
dynamics
of
the
proposed
functional probabilistic
approach
is
not
Newton's
equation,
but
a Liouville
equation
for
distribution
function.
It
is well known
that
the
Liouville equa-
tion
is used in
statistical
mechanics for
the
description
of
the
motions
of
gas.
Let
us
stress
that
we shall use
the
Liouville
equation
for
the
description
of
a single
particle
in
the
empty
space.
A Liouville
equation
on
the
manifold f
with
coordinates
x =
(xl,
... ,
xk)
has
the
form
k
[)p
,,[)
i
[)t
+ L
[)x
Jpv
) = 0 .
i=1
(1)
Here p = p(x, t) is
the
probability
density function
and
v =
v(x)
=
(vI, ... , v
k
) -
vector field
on
f.
The
solution
of
the
Cauchy
problem
for
the
equation
(1)
with
initial
data
(2)
might
be
written
in
the
form
(3)
Here
CPt
(x) is a
phase
flow along
the
solutions
of
the
characteristic
equation
X=v(x).
(4)
Let
(q,p)
be
co-ordinates
on
the
plane
ffi.2
(phase space), t E
ffi.
is time.
The
state
of
a classical
particle
at
time
t will
be
described
by
the
function
p =
p(
q,
p,
t),
it
is
the
density
of
the
probability
that
the
particle
at
time
t
has
the
coordinate
q
and
momentum
p.
Therefore, in
the
functional
approach
to
classical mechanics
the
concept
of precise
trajectory
of a
particle
is
absent,
the
fundamental
concept is a
distribution
function p = p(q,p, t)
and
D-function
as
a
distribution
function
is
not
allowed.
We
assume
that
the
continuously differentiable
and
integrable
function
p
= p(
q,
p, t) satisfies
the
conditions:
p
~
0, r p(q,p, t)dqdp =
1,
t E
ffi..
ill!.2
(5)
If
f = f(q,p) is a function
on
phase
space,
the
average value
of
f
at
time
t is given
by
the
integral
(f)(t)
= J f(q,p)p(q,p, t)dqdp.
(6)

366
In a sense
we
are
dealing
with
a
random
process
~(t)
with
values in
the
phase
spac
e.
Motion
of
a
point
body
along a
straight
line in
the
potential
field will
be
described
by
the
equation
8p p 8p 8V(q) 8p
8t
= - m 8q +
--;)g
8p .
(7)
Here V(q) is
the
potential
field
and
mass
m >
O.
If
the
distribution
Po(q,p) for t = 0 is known, we
can
consider
the
Cauchy
problem
for
the
e
quation
(7):
plt=o
= Po(q,p)·
(8)
The
mean
trajectori
es defined as follows
(q)(t) = J qp(q,p, t)dqdp = J q(t)Po(q,p)dqdp,
(9)
where q(t) - is a classical
trajectory
of a
point
mass
,
the
function q(t) is
governed
by
Newton
equ
a
tion
..
8V(q)
mq
=--;)g'
Therefor
e
the
mean
trajectory
can
be
obtained
by
averaging classical
trajectory
with
reference
to
probability
distribution
function for initial con-
ditions.
This
fact will
be
widely used
in
the
present work.
2.
Anharmonic
oscillator
In
the
present
work
an
anharmonic
oscillator is considered.
Namely
a
point
mass
is moving
within
a field
that
is described by
the
potential
V(q):
1 1
V(q) =
2w6q2
+=
t::
q4
(10)
where
Wo
> 0
and
E > 0 is a
small
coupling
constant.
The
coordinate
q(t)
changes
in
accordance
with
the
Newton
equation:
q +
W6q
= _
Eq
3.
(11)
We
set
the
following initial conditions:
(12)
The
exact
solution
to
(11) is well-known
but
for simplicity we shall use
the
approximate
Krylov-Bogolyubov
method
described for
example
in
9.
The
solution reads:
a
3
qKB(t) = acos(tw) + E
32w5
cos(3tw) +
O(E2),

367
where a is
an
arbitrary
constant
and
is
the
frequency w depends
on
para-
meter
a as follows:
3
w = w(a) =
wo(1
+
Sa
2
c + O(c
2
)).
From
the
initial conditions (12)
we
get
(13)
We
write
and
we
have
qKB(O,
b)
=
b.
The
mean
value
of
coordinate
in
the
functional mechanics
we
define by
the
integral
(b
- b
O
)2
11-
(q)(t,
CJ)
=
r;;:;;
qKB(t, b)e
CJ
db
V
CJ1r
IR
(14)
with
the
distribution
function
Po(b)
= exp{
-(b-
b
O
)2
/CJ}
/
ViW.
Here
CJ
> °
is dispersion.
Note
that
(q)(O,
CJ)
=
boo
We
want
to
compare two
time
dependent
functions: (q)(t,
CJ)
and
qKB(t, b
o
).
For small t
the
difference between
them
is small since
(q)(O,
CJ)
=
qKB(O,
b
o
) =
boo
The
question is
what
is
the
char-
acteristic
threshold
value
tc
such
that
for t >
tc
the
difference between
the
two functions become
rather
big
and
what
is
the
dependence of
tc
=
tc(CJ)
from
the
dispersion
CJ?
Note
that
the
analogous problem of
the
dependence
of
the
characteristic
time
from
the
Planck
constant
is considered in
8.
3.
Newtonian
and
Averaged
Trajectories
Comparison
It
was proved
in
1
that
for
any
time
t one has
lim
(q)(t,
CJ)
= qKB(t, b
o
).
a-+O
That
is why one should
expect
tc(CJ)
to
increase
with
CJ
-->
0.
One
can
assume
without
loss
of
generality
that
Wo
= 1.
The
real
roots
of
the
cubic
equation
(13)
are
given by
the
following function
10:
a =
a(b)
=
S{£
sinh(~arCSinh(~f¥bo))

368
Let us
introduce
the
following change of variables in
the
integral (14):
zva
+ b
o
=
b.
It
yields
(q)(t,
O")
=
In
1
(a(zVa
+ b
o
) cos(tw(zVa + b
o
))+
E(a(zva+bo))3
2
+ 32
cos(3tw(zva
+ bo)))e-
Z
dz
(15)
One
can
make a rough
estimate
of
the
threshold
time
tc
by using
the
method
of
steepest
descent. In
this
way we get
tc
=
0(1/
va)
as
0"
--7
O.
4.
Numerical
Approach
One
of
the
ways
to
compare functional mechanical
mean
value
of
coordi-
nate
and
trajectory
obtained
by means
of
perturbations
theory
is
estimate
dependence
time
tthr
of
convergence
on
dispersion
0"
of initial condition
b.
To define
the
threshold
time
we consider
the
following function
L\(t) = I(q)(t,
0")
- qKBM(t,
bo)1
(16)
so
that
the
moment
of
time
tc
=
tthr(O",
C)
is
the
minimal value
of
time
t
when
the
absolute value of
the
function L\(t) equals some positive value C
(17)
For
instanc
e,
constant
C
can
be
put
equal
to
b
o
.
In
order
to
carry
out
numerical
estimations
one
has
to
define
constants
as follows E = 0.1, b
o
= 0.
5.
The
classical
and
averaged
trajectories
for
different
time
intervals are
plotted
on
the
figures below.
The
classical
and
averaged
trajectories
are
represented by
the
dashed
and
solid lines respec-
tively.
One
can
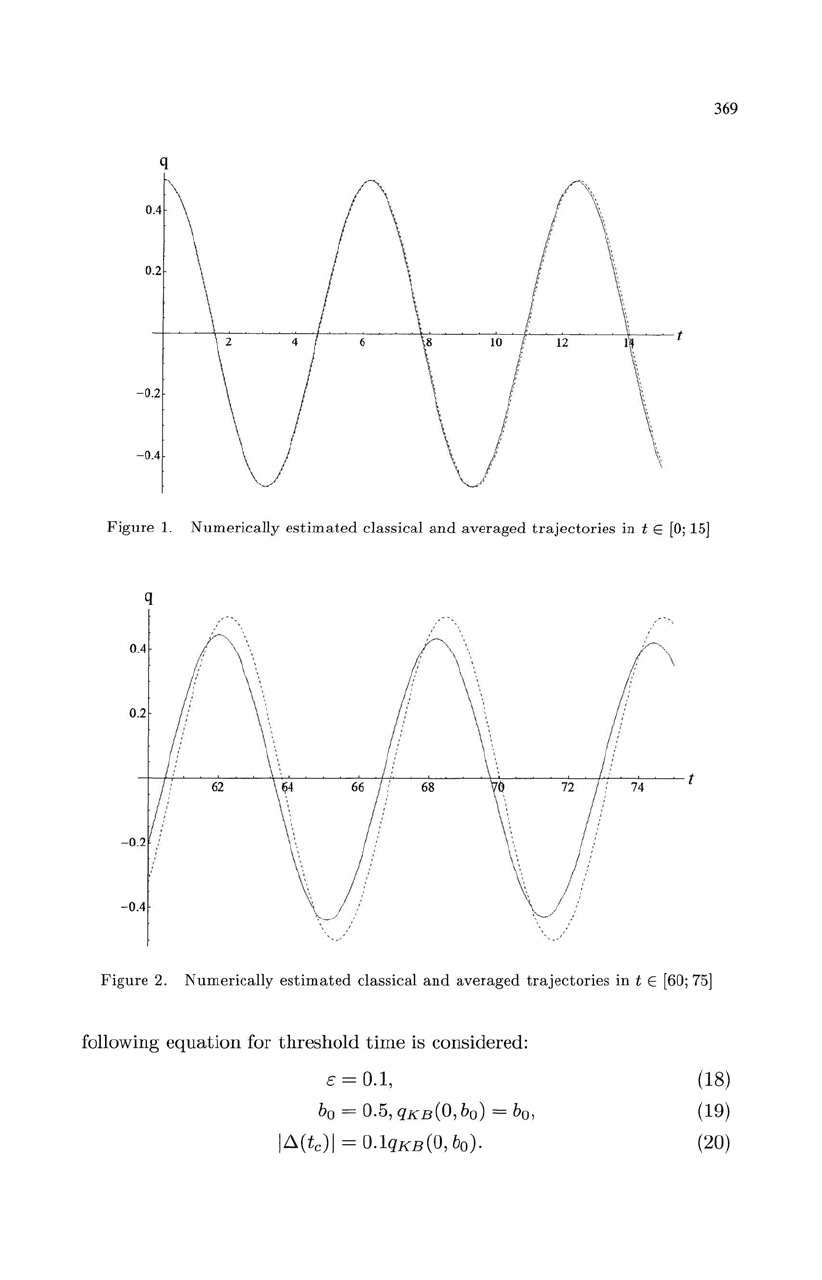
see from Fig. 1
that
the
divergence between classical
and
averaged
trajectories
is less
than
E for t E
[0;
15].
On
the
Fig. 2
it
is shown
that
the
amplitude
of
the
averaged
trajectory
is decreasing
with
time, con-
sequently
the
divergence between
the
trajectories
is increasing. Also one
can
see
that
the
phase
shift between oscillations becomes easily observed
(Fig. 2).
The
averaged
trajectory
amplitude
tends
to
zero
with time
(Fig 3) while
the
phase
difference
of
the
oscillations does
not
seem
to
have
any
limit value.
In
order
to
move
further
and
make
estimations
of
tc
for different values
of
0"
it
is necessary
to
define
constant
C =
O.lqKB(O,
b
o
).
So
that
the
q
0.4
0.2
-0.2
-0.4
/'.
I '
f \
! \
i \
I ,
I \
f \
I \
/ \
I \
I \
, \
369
Figure
1.
Numerically
estimated
classical
and
averaged
trajectories
in
t E
[0;
15]
q
Figure
2.
Numerically
estimated
classical
and
averaged
trajectories
in
t E [60;
75]
following
equation
for
threshold
time
is considered:
E = 0.1,
b
o
= 0.5, qKB(O, b
o
)
= b
o
,
1~(tc)1
= O.lqKB(O, b
o
).
(18)
(19)
(20)
