Accardi L., Freudenberg W., Obya M. (Eds.) Quantum Bio-informatics IV: From Quantum Information to Bio-informatics
Подождите немного. Документ загружается.


390
Moreover,
the
noisy
quantum
channel
with
the
vacuum noise
state
~o
=
10)
(01
is called
the
attenuation
channel
Ao
given by Ohya 19 as
(3)
which are
important
to
discuss
the
quantum
communication processes.
3.
Complexities
In
ID
22,
two kind of complexities CS (p),
TS
(p;
A *) are used for
studying
the
complex systems. CS
(p)
is
a complexity of a
state
p measured from
a subset
Sand
T
S
(p;
A *)
is
a
transmitted
complexity associated
with
the
state
change from p
to
A * p. These complexities should satisfy
the
follow-
ing conditions: Let
S
,S,
St be subsets of 6
(Hd
, 6 (H
2
) , 6
(H1
® H2),
respectively.
(1) For any
PES,
CS
(p)
and
TS
(p;
A *) are nonnegative.
(2) For a bijection
j from
ex6(H
1
)
to
ex6(H
1
),
CS(p)
is
equal
to
CS(j
(p)), where
ex6
(Hd
is
the
set
of extremal
point
of 6
(Hd.
(3) For p ® a E 6
(H1
® H
2
),
p E 6
(Hd,
a E 6 (H
2
),
the
complexity
CSt
(p ® a) of
the
state
p ® a of
totally
independent systems
is
equal
to
the
sum
C
S
(p)
+ C
S
(a) of
the
complexities of
the
states
p
and
a.
(4)
The
transmitted
complexity
TS
(p;
A *) is
greater
than
0
and
it
is
less
than
the
complexity C
S
(p)
of
the
state
p.
(5)
If
the
channel A * is
the
identity
map
id,
then
T
S
(p
; id) is equal
to
CS(p).
One of
the
example of
the
above complexities are
the
Shannon
entropy
S
(p)
for CS
(p)
and
classical
mutual
entropy I
(p;
A *) for
TS
(p;
A *). Let
us consider these complexities for
quantum
systems.
3.1.
Example
of
Complexity
C
S
(p)
3.1.1.
(1)
von
Neumann
entropy
One of
the
example of
the
complexity C
S
(p)
of ID in
quantum
system is
the
von
Neumann
entropy
17
S
(p)
described by
C
S
(p)
{:}
S(p)
=
-trplogp
for any density
operators
p E 6
(Hd,
which satisfies
the
above conditions
(1), (2), (3).

391
3.1.2.
(2)
S-mixing
entropy
Let
(A,
6(A),
a(G))
be
a
C*-dynamical
system
and
S
be
a weak*
compact
and
convex
subset
of
6(A).
For
example, S is given
by
6(A)
(the
set
of
all
states
on
A),
I(a)
(the
set
of
all
invariant
states
for a ),
K(a)
(the
set
of
all KMS
states),
and
so on.
Every
state
rp
E S
has
a
maximal
measure
fL
pseudosupported
on
exS
such
that
rp
=
is
wdfL,
(4)
where
exS
is
the
set
of
all
extreme
points
of
S.
The
measure
fL
giving
the
above decomposition is
not
unique
unless S is a
Choquet
simplex. We
denote
the
set
of all such measures by M",(S),
and
define
D",(S) = {M",(S);
3fLk
c
jR+
and
{rpd
c
exS
s.t.
~fLk
=
1,
fL
=
~fLk8(rpk)}'
(5)
where 8(rp) is
the
Dirac
measure
concentrated
on
an
initial
state
rp.
For a
measure
fL
E D",(S), we
put
H(fL)
= -
LfLklogfLk·
k
(6)
The
C*-entropy of a
state
rp
E S
with
respect
to
S
(S-mixing
entropy)
is defined
in
21
by
SS(rp) = {
inf
{H
(fL);
fL
E D",(S)}
+00
if D",(S) =
0.
(7)
It
describes
the
amount
of
information
of
the
state
rp
measured
from
the
subsystem
S.
We
denote
S6(AJ(rp)
by
S(rp) if S =
6(A).
It
is
an
extension
of
von
Neumann's
entropy.
This
entropy
(mixing
S-entropy)
of
a general
state
rp
satisfies
the
fol-
lowing
properties
21.
Theorem
3.1.
When A =
B(H)
and
at
=
Ad(U
t
) (i.e.,
at(A)
=
Ut
AUt
for
any
A E
A)
with
a
unitary
operator
Ut,
for
any
state
rp
given
by
rp(.) =
trp·
with
a density
operator
p, the
following
facts
hold:
(1)
S(rp) =
-trplogp.
(2)
If
rp
is
an
a-invariant
faithful
state
and
every eigenvalue
of
p is
non-degenerate,
then
SI(a.J(rp) = S(rp), where I
(a)
is
the
set
of all
a-invariant
faithful
states.

392
(3)
If
ep
E K(n:),
then
sK(al(ep) = 0, where K (n:)is
the
set
of all KMS
states.
Theorem
3.2.
For any
ep
E K(n:) , one can obtain
(1) sK(al(ep)
:::;
sI(al(ep).
(2) sK(al(ep)
:::;
Seep).
3.2.
Example
of
Transmitted Complexity
rs (Pi A
*)
3.2.1.
(1)
Ohya
mutual
entropy
for
density
operator
An
example of
the
transmitted
complexity T
S
(p;
A
*)
of ID in
quantum
system is
the
Ohya
mutual
entropy
with
respect
to
the
initial
state
p
and
the
quantum
channel A * defined in
19
by
T
S
(p;
A*)
~
J
(p;
A*)
==
sup
{~S(O'E'P@A*P)'P
=
~AnEn}'
(8)
where
0'
E is
the
compound
state
given by
0'
E =
2::n
AnEn@A * En associated
with
the
Schatten-von
Neumann
(one dimensional spectral) decomposition
30
p =
2::n
AnEn of
the
input
state
p,
and
S (',
.)
is
the
Umegaki's relative
entropy denoted by
S(
)
=
{trp(lOgp-IogO')
(whenranpcranO')
p,O'
-
(h
.)
00
ot
erWlse
(9)
which was
extended
to
more general
quantum
systems by Araki
and
Uhlmann
5,20,23,32.
The
Ohya
mutual
entropy holds
the
above conditions
(4)
such as
0:::;
J(p,A*):::;
S(p).
3.2.2. (2)
Ohya
mutual
entropy
for
general
C*-system
Let
(A,6(A),n:(G))
be a
unital
C*-system
and
S
be
a weak* compact
convex subset of
6(A).
For
an
initial
state
ep
E S
and
a channel
A*
:
6 (A)
-+
6 (B), two
compound
states
are
<P~
=
Is
w @A*w
dj1,
<Po
=
ep@A*ep.
(10)
(11)

393
The
compound
state
if>~
expresses
the
correlation between
the
input
state
c.p
and
the
output
state
A*c.p.
The
mutual
entropy
21
with
respect
to
Sand
f.L
is given by
I~
(c.p
; A *) = s
(if>~,
if>o)
and
the
mutual
entropy
with
respect
to
S is defined
by
Ohya
21 as
IS
(c.p
; A
*)
=
sup
{I~
(c.p
; A
*)
;
f.L
E
Mtp
(S)}
.
4.
Quantum
Mean
Mutual
Entropy
of
K-S
type
(12)
(13)
In
this
section, we briefly review
quantum
mean
entropy
and
quantum
mean
mutual
entropy
introduced
by
Ohya
21.
A
stationary
information source
in
quantum
information
theory
is de-
scribed by a
C*triple
(A,
6(A),
()
A)
with
a
stationary
state
c.p
with
respect
to
()
A;
that
is, A is a
unital
C*
-algebra
,
6(A)
is
the
set of all
states
on
A, ()A is
an
automorphism
of
A,
and
c.p
E
6(A)
is a
state
over A
with
c.p
0 ()A =
c.p.
Let
an
output
C*-dynamical
system
be
the
triple
(8,6(8),
()s),
and
A * :
6(A)
--->
6(8)
be
a covariant c.p. channel: A : 8
--->
A such
that
A 0
()s
=
()
A 0
A.
In
this
section
we
exp
lain new functionals
S~(c.p;aM),
SS(c.p;a
M
),
I~
(c.p;
aM,
f3N)
and
IS
(c.p;
aM,
f3N)
introduced
in
21,16
for a
pair
of
finite se-
quences
of
aM = (aI, a2, .
..
, aM),
f3N
=
(13
1
,13
2
,
.
..
,13
N)
of
completely
positive
unital
maps
am
:
Am
--->
A,
f3
n
:
8
n
--->
8 where
Am
and
8
n
(m
= 1, ·· ·
,M,
n = 1,
···
,N)
are
finite dimensional
unital
C*-algebras.
For a given finite sequences
of
completely positive
unital
maps
am
:
Am
--->
A from finite dimensional
unital
C*
-algebras
Am
(m
=
1,··
.
,M)
and
a given measure
f.L
of
c.p
E Mtp(S),
the
compound
state
of
M
aic.p,
a2c.p,
...
,aMc.p
on
th
e
tensor
product
algebra
®
Am
is given by 21,
16
m=l
M
if>~(aM)
= r
Q9
a:nw
df.L(w).
JS(A)
m=l
(14)
Furthermore
if>~(aM
U
f3N)
is a
compound
state
of
if>~(aM)
and
if>~(f3N)
with
aM U
f3N
==
(aI,
a2,···
,aM,
131,
132,···
,f3
N
)
constructed
as
if>~
(aM U
f3N)
= 1
(~a:nw)
(db
f3~W)
df.L.
(15)
SeA
) m = l
n=l

394
For
any
pair
(aM,
(3N)
of finite sequences aM = (aI,
...
, aM)
and
(3N
=
((31'
...
,
(3N)
of
completely positive
unital
maps
(c.p.u.
maps
for
short)
am
:
Am
----;
A,
(3n
: 8
n
----;
A from finite dimensional
unital
C*
-algebras
and
any
extremal
decomposition measure
J.L
of
rp,
the
entropy
functional
SIL
and
the
mutual
entropy
functional III
are
defined by
21,16
S~(rp;aM)=
r
S((6>::;=la:nw,<P~(aM))dJ.L(w),
(16)
J
SeA)
I~
(rp;
aM,
(3N)
= S (
<P~
(aM U
(3N),
<P~
(aM)
(6)
<I>~
((3N)) ,
(17)
where S(·,·) is
the
relative
entropy
for a finite algebra.
The
relative
entropy
of
two
states
was
introduced
in
31
for O'-finite
and
semi finite von
Neumann
algebras. Araki 5
and
Uhlmann
32
extended
this
relative
entropy
for more
general
quantum
systems
23.
For a given
pair
of finite sequences
of
completely positive
unital
maps
aM = (a1,'"
,aM),
(3N
=
((31''''
,
(3N),
the
functional SS(rp;a
M
) (resp.
IS(rp;a
M
,(3N)) is given by
taking
the
supremum
of
S~(rp;aM)
(resp.
I~(rp;
aM,
(3N))
for all possible
extremal
decompositions
J.L'S
of
rp:
SS(rp;a
M
) =
sup{S~(rp;aM);
J.L
E M<p(S)},
(18)
IS(rp;a
M
,(3N) =
sup{I~(rp;aM,(3N);
J.L
E
M<p(S)}.
(19)
Let A (resp.
8)
be
a
unital
C*
-algebra
with
a fixed
automorphism
804
(resp.
8{3),
A
be
a covariant c.p.u.
map
from 8
to
A,
and
rp
be
an
invariant
state
over A, i.e.,
rp
0
804
=
rp.
N - ( 8 8
N
-
1
)
a = a, A 0 a,
...
, A 0 a ,
(3f..
==
(Ao(3,A
0
8{30(3
, '" ,A
0
8;;- 1
0(3).
(20)
(21)
For each c.p.u.
map
a : Ao
----;
A (resp.
finite dimensional
unital
C*
-algebra
Ao (resp.
§S(rp;8
A
,a),
jS(rp;A*,8
A
,8{3,a,(3)
are
given by
(3
: 8
0
----;
8)
from a
8
0
)
to
A (resp.
8),
jS
(rp;
A *,8
04
,
8{3,
a,
(3)
= lim
sup
N
1
IS
(rp;
aN,
(3f..).
(23)
N-+oo
The
functionals
§s
(rp;
804)
and
jS
(rp;
A
*,804,
8{3)
are
defined by
taking
the

395
supremum
for all possible Ao's,
a's,
Bo's,
and
(3's:
SS(<P;BA)
=supSs(<p;BA,a),
(24)
<>
-s
*
-s
*
I
(cp;A
,BA,Bs) =
supI
(cp;A
,B
A
,B
s
,a,(3).
(25)
<>,(3
The
next
theorem
21
,16
shows
that
the
fundamental
ine
quality
in
informa-
tion
theory
holds for
SS(<P;BA)
and
jS(
cp;
A*,BA,B
s
).
Theorem
4.1.
o:s;
jS(cp;A*,BA,Bs):S; min{SS(cp;BA),SS(A*cp;Bs)}.
4.1.
Computation
of
mean
mutual
entropy
for
modulated
states
of
OOK
and
PSK
Let B(rto) (resp. B(rto))
be
the
set
of all
bounded
linear
operators
on
a
Hilbert
spac
e rto (resp. {to)
and
Ao
(resp.
Bo)
be
a finite subset
in
B(rt
o
)
(resp. B(rto)).
Let A (resp.
B)
be
an infinite
tensor
product
space of B(rto) (resp.
B(rt
o
))
re
pr
esented by
00 00
A
==
0 B(rto), B
==
0 B(rto).
i
=-
oo
i=-oo
Moreover, let
BA
(resp. Bs)
be
a shift
transformations
on
A (resp.
B)
defined by
00
00
00
i=-oo
i'=-ex>
i=
-
CXJ
00
00
00
j
=-oo
j'
=
-oo
j =
-oo
Let a (resp.
(3)
be
the
embedding
map
from
Ao
to
A , (resp.
Bo
to
B)
given
by
a(
A) =
...
I ® I ® A ® I ® .
..
E
A,
for
any
A E Ao,
(3(B)
=
...
I ® I ® B ® I ®
...
E
B,
for
any
B E B
o
.
We
denote
the
set
of all density
operators
on
rto (resp. rto) by
60
(resp.
(
0
),
and
let 6 (resp.
6)
be
the
set
of
all
states
p
on
A (resp. p
on
B).
The
maps
afM)'
(3r(M)
are
given by
N ( - B - B
N
-
1
- )
aiM)
==
aO'(M)'
Aoao'(M),"',
A
oao'(M)'
(3r(M)
==
(1(
M)
0
J...
0
(3,
1(
M)
0
J...
0
Bs
0 (3,'" , 1(M) 0
J...
0
B;-l
0
(3),

396
00
where
we
took
a special channel
and
modulators
M such
that
A
==
® A
00
and
i(M)
==
®
I(M)'
i=-(X)
4.1.1.
Mean
mutual
entropy
for
modulated
state
of
OOK
and
PSK
00 00
i= -
oo
For
an
initial
state
p(M)
to\
(M)
E
I.(Y
Pi
® 6
i
(M
=
OaK,
PSK),
i=-oo
i=-CXJ
p~OOK)
and
p~PSK)
are
given by
p~OOK)
= v
10)
(01
+
(1
-
v)
I,,;)
(,,;1,
p~PSK)
= v
1-,,;
)
(-,,;1
+
(1-
v)
I,,;)
(,,;1
(0::; v
::;
1).
The
Schatten
decomposition
of
p~M)
is
obtained
as
2
pi
M
)
= L
A~)
E~~)
,
ni=l
where
the
eigenvalues
A~~)
of
pi
M
)
are
A~
~O
K
)
=
~
{l+(_l)k-l
V
1
-
4v(1-
v)
(1-
exp
(-1,,;1
2
))
},
Ar:,SK)
=
~
{l+(_l)k-l
V1-
4v(1-
v)
(1-
exp
(-2
1
,,;1
2
))}
(k = 1,
2)
.
Two
projections
E~~
)
(ni
(ni
= 1,2) are given by
1,
2)
and
the
eigenvectors
le~~
))
of
A~~)

397
where
For
the
above initial
state
E~A(),
one
can
obtain
the
output
state
for
the
attenuation
channel
Ao
as follows:
2
A*E~A()
= L
:\~~~;E~7~;
(ni =
1,
2),
n~=l
.
~(M)
(M)
.
where
the
eIgenvalues
An
i,
n;
of A * Eni are gIven by (ni =
1,2),
(k =
1,2)
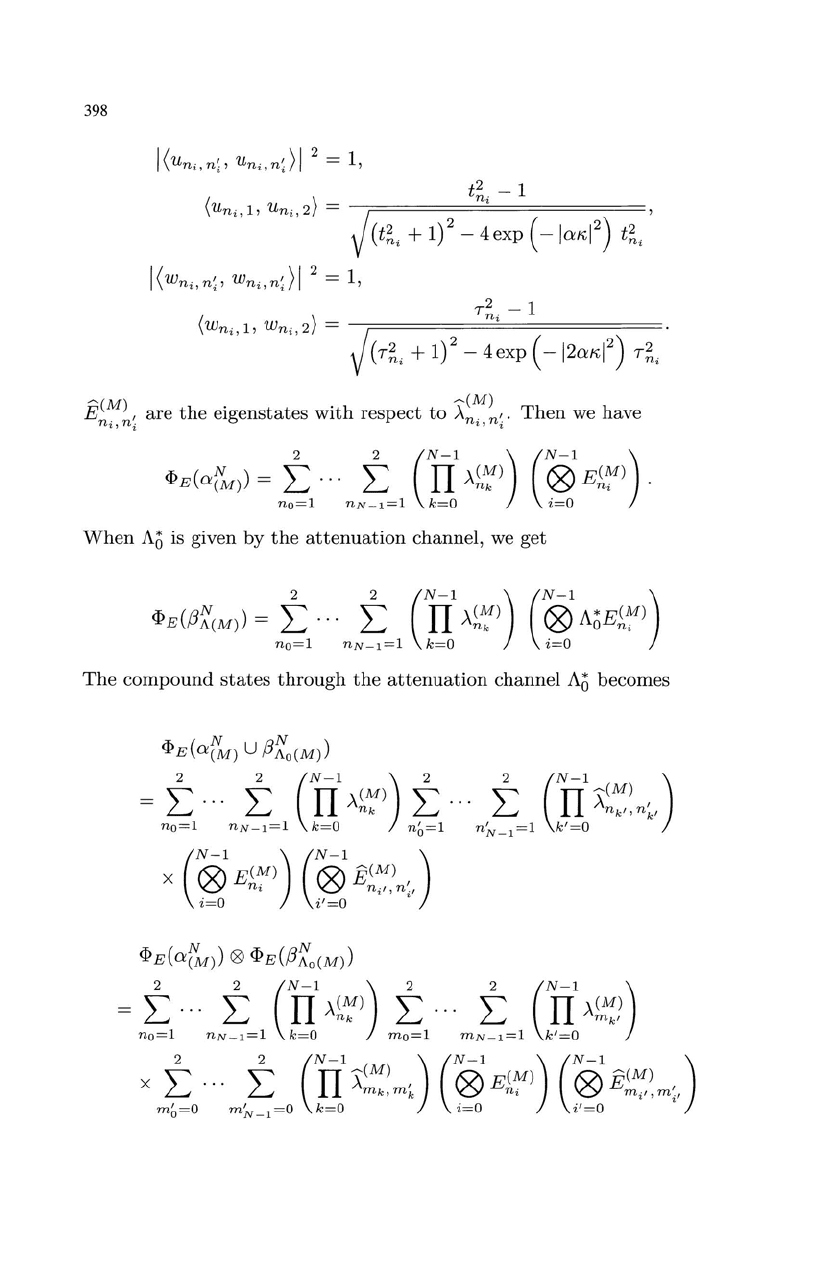
398
When
AD
is given by
the
attenuation
channel, we get
The
compound
states
through
the
attenuation
channel
Ao
becomes
iI>
E (a[11)) ®
iI>
E
({3;:;'o
(M))
=
i;l···
nNf:=l
(IT
A~~))
m~l
mt=l
Crr:
A~:)
x
Jo
mt
~o
(IT
~;:::
m~)
(~E~:'l)
(~E~~:
m:,
)

399
00 00
Lemma
4.1.
For an initial state
p(M)
=
(8)
pi
M
)
E
(8)
6
i
,
we have
i=-oc>
i=-OCJ
IE(p(M);
arM)'
fJraOK))
~
nt,··
·n'Nt.dn~'···
nNt
m:
A~~'lX;'~)nl)
By using
the
above lemma, we have
the
following theorems.
00 00
Theorem
4.2.
For an initial state
p(M)
=
(8)
pi
M
) E
(8)
6
i
i=-oo i=-oo
(M
=
OOK,
PSK),
we
have
S(p(M);
()A,
arM))
=
J~oo~S(p(M);
arM))
2
= - L
A~M)
log
A~M)
n=l
and
I
-(p(
M).
A*
()A
()B
n,N
a.
N
)
, , ,
''-'(M)'
fJ(M)
2 2
~(M)
_
""
(M)~(M)
An,
n'
- 0 0
An
An,
n'
log
-----=-2----'---
n'=l
n=l
" A
(M)>..(M)
~
m
m,n'
m=l
00
00
Theorem
4.3.
For an initial state
p(M)
=
(8)
pi
M
)
E
(8)
6
i
i=-OCJ
(M
=
OOK,
PSK),
one has the following inequalities:
(1)
S
-(
(PSK).
()
N ) S-(
(OOK).
()
N )
P
,A,
a(PSK)
2':
p
,A,
a(OOK)
,
i=-OCJ
