Accardi L., Freudenberg W., Obya M. (Eds.) Quantum Bio-informatics IV: From Quantum Information to Bio-informatics
Подождите немного. Документ загружается.


350
28.
Tomizawa
,
S.
and
Machida, M. (1999).
Measure
of
proportional
reduction
in
variation
for multi-way contingency
tables
with
multiple
response variables.
The Egyptian Statistical Journal,
43,
167-182.
29. Tomizawa,
S.
and
Tahata,
K.
(2007).
Th
e analysis
of
symmetry
and
asymme-
try:
orthogonality
of
decomposition
of
symmetry
into
quasi-symmetry
and
marginal
symmetry
for multi-way
tables.
Journal
de
la
Societe Francaise
de
Statistiqu
e,
148,
3-36.
30. Tomizawa,
S.
and
Yukawa,
T.
(2003).
Proportional
reduction
in
variation
measures
of
departure
from
cumulative
dichotomous
independence
for
square
contingency
tables
with
same
ordinal
classifications. Far East Journal
of
The-
oretical Statistics,
11,
133-165.
31. Tomizawa,
S.
and
Yukawa,
T.
(2004).
Proportional
reduction
in
variation
measure
for two-way contingency
tables
with
ordered
categories. Journal
of
Statistical Research,
38,
45-59.
32. Tomizawa,
S.,
Miyamoto,
N.
and
Yajima,
R. (2002).
Proportional
reduction
in
variation
measure
for
nominal-ordinal
contingency tables. Calcutta Statis-
tical Association Bulletin,
53,
167-183.
33.
Tomizawa
, S.,
Miyamoto,
N.
and
Yamamoto,
K.
(2006).
Decomposition
for
polynomial
cumulative
symmetry
model
in
square
contingency
tables
with
ordered
categories. Metron,
64,
303-314.
34. Tomizawa,
S., Seo,
T.
and
Ebi, M. (1997). Generalized
proportional
reduction
in
variation
measure
for two-way
contingency
tables. Behaviormetrika, 24,
193-201.
35.
Yamamoto,
K.
and
Tomizawa
,
S.
(2009).
Measure
of
proportional
reduction
in
variation
and
measure
of
agreement
for contingency
tables
with
ordered
categories. International Journal
of
Applied Mathematics and Statistics, 14,
3-23.
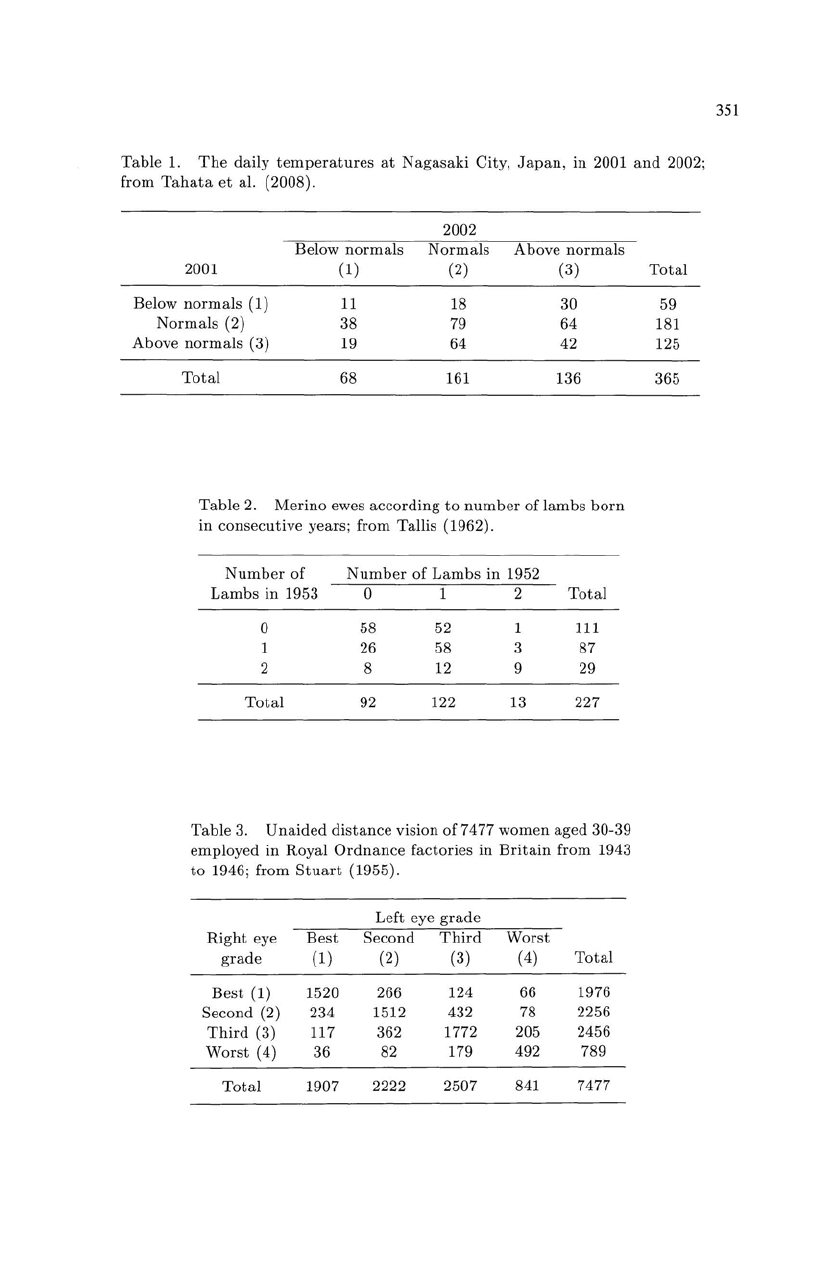
Table
1.
The
daily
temperatures
at
Nagasaki
City,
Japan,
in
2001
and
2002;
from
Tahata
et
al. (2008).
2002
Below
normals
Normals
Above
normals
2001
(1)
(2) (3)
Below
normals
(1)
11
18
30
Normals
(2)
38 79 64
Above
normals
(3) 19
64 42
Total
68 161 136
Table
2.
Merino
ewes
according
to
number
of
lambs
born
in
consecutive
years;
from
Tallis (1962).
Number
of
Number
of
Lambs
in 1952
Lambs
in 1953
0 1 2
Total
0 58 52
1
111
26 58 3
87
2 8 12 9 29
Total
92 122 13 227
Table
3.
D
naided
distance
vision of 7477
women
aged
30-39
employed
in
Royal
Ordnance
factories
in
Britain
from 1943
to
1946; from
Stuart
(1955).
Left
eye
grade
Right
eye
Best
Second
Third
Worst
grade
(1) (2) (3)
(4)
Total
Best
(1)
1520 266
124
66
1976
Second
(2)
234 1512
432 78 2256
Third
(3)
117 362
1772 205 2456
Worst
(4) 36
82
179 492 789
Total
1907
2222 2507
841 7477
Total
59
181
125
365
351
352
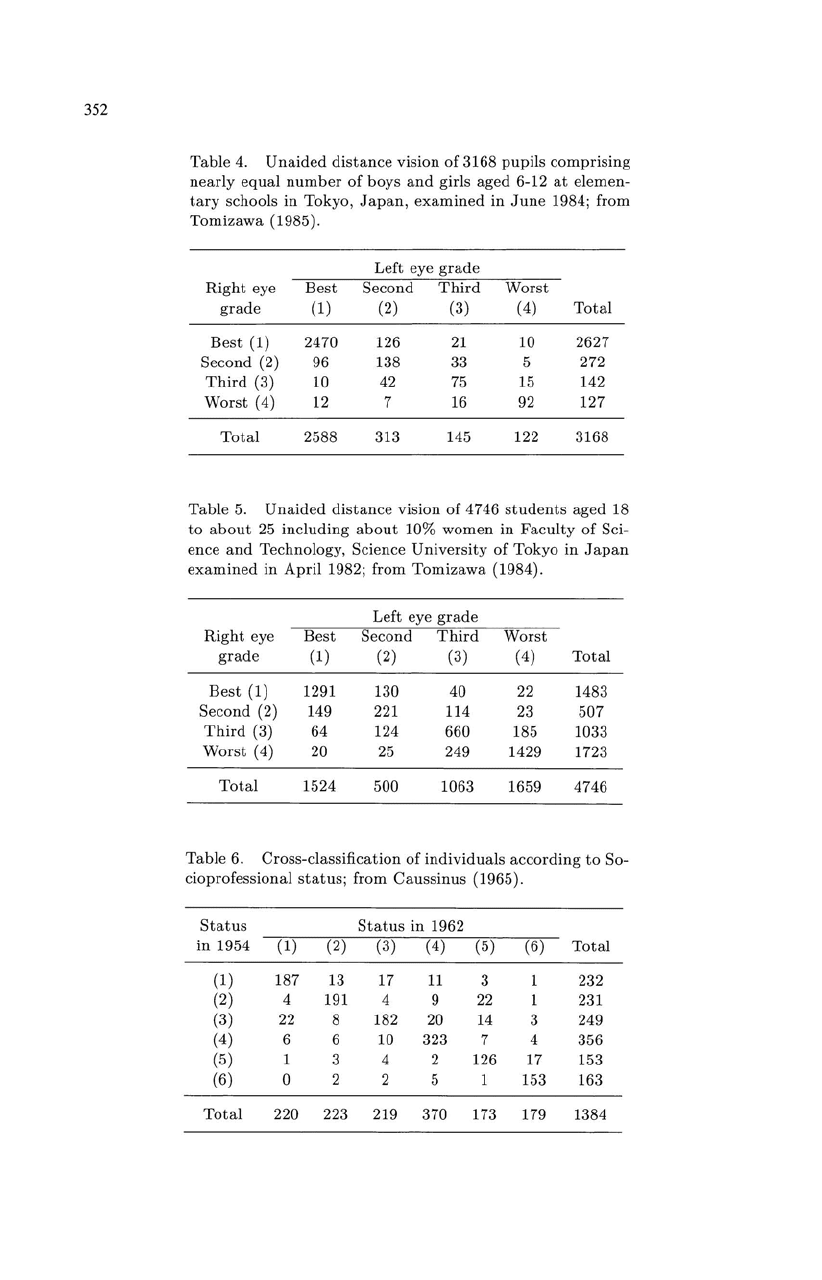
Table
4.
Unaided
distance
vision
of
3168
pupils
comprising
nearly
equal
number
of
boys
and
girls
aged
6-12
at
elemen-
tary
schools in
Tokyo,
Japan,
examined
in
June
1984; from
Tomizawa
(1985).
Left
eye
grade
Right
eye
Best
Second
Third
Worst
grade
(1) (2) (3)
(4)
Total
Best
(1)
2470 126
21
10 2627
Second
(2) 96 138 33 5
272
Third
(3) 10 42
75
15
142
Worst
(4) 12 7 16 92 127
Total
2588
313 145 122 3168
Table
5.
Unaided
distance
vision
of
4746
students
aged
18
to
about
25
including
about
10%
women
in
Faculty
of
Sci-
ence
and
Technology, Science
University
of
Tokyo
in
Japan
examined
in
April
1982; from
Tomizawa
(1984).
Left
eye
grade
Right
eye
Best
Second
Third
Worst
grade
(1) (2)
(3)
(4)
Total
Best
(1) 1291 130 40
22 1483
Second
(2) 149 221 114
23
507
Third
(3)
64 124
660 185 1033
Worst
(4) 20
25 249 1429
1723
Total
1524
500 1063
1659 4746
Table
6.
Cross-classification
of
individuals
according
to
So-
cioprofessional
status;
from
Caussinus
(1965).
Status Status
in
1962
in 1954 (1) (2)
(3) (4) (5)
(6)
Total
(1) 187 13
17
11
3
232
(2) 4
191 4
9
22 1
231
(3) 22
8
182
20
14 3 249
(4)
6 6
10 323
7
4
356
(5) 1
3
4 2 126 17
153
(6)
0
2
2 5 1 153 163
Total
220 223 219
370 173 179 1384
353
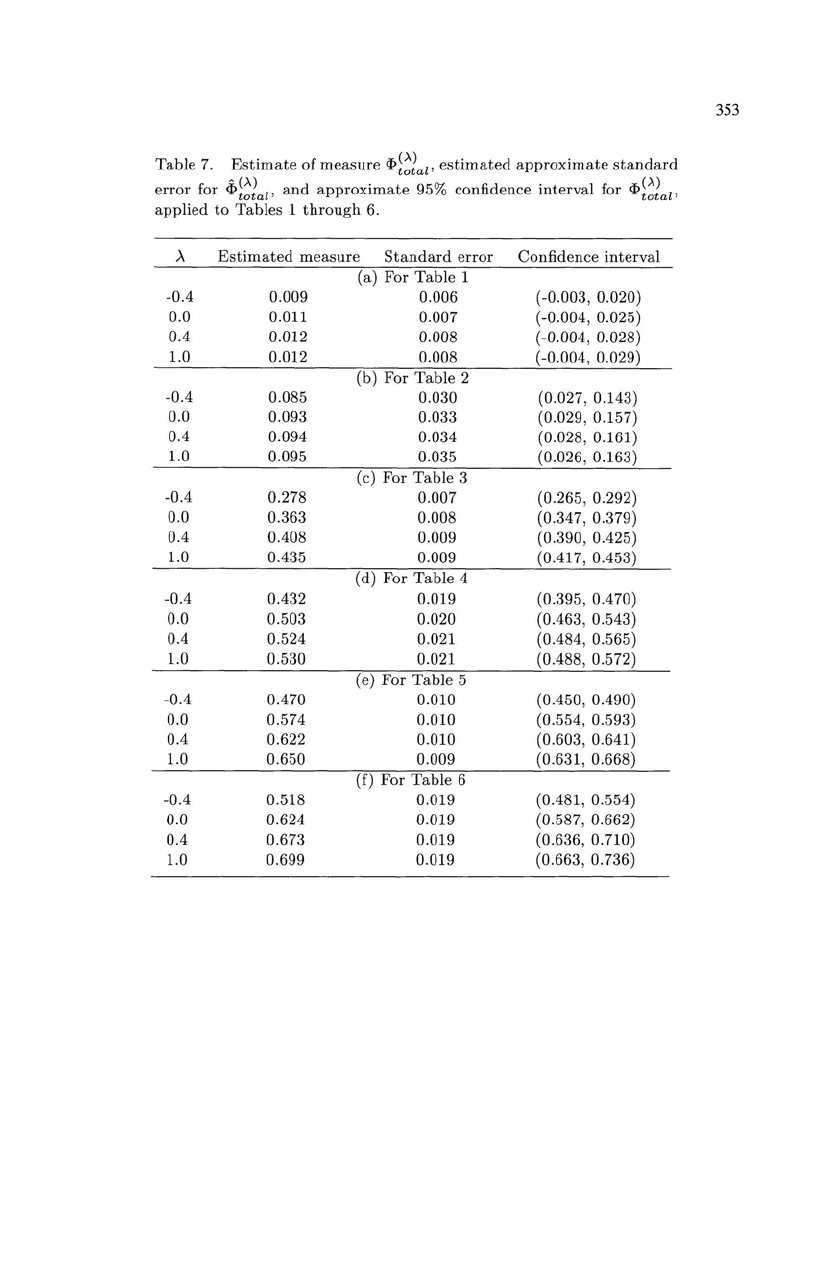
Table
7.
Estimate
of
measure
<p~~lal'
estimated
approximate
standard
error
for
4:>~~lal'
and
approximate
95% confidence
interval
for
<p~~lal'
applied
to
Tables
1
through
6.
.A.
Estimated
measure
Standard
error
Confidence
interval
(a)
For
Table
1
-0.4
0.009 0.006
(-0.003, 0.020)
0.0 0.011
0.007 (-0.004, 0.025)
0.4
0.012 0.008
(-0.004, 0.028)
1.0 0.012
0.008
(-0.004, 0.029)
(b)
For
Table
2
-0.4 0.085
0.030
(0.027, 0.143)
0.0 0.093
0.033
(0.029, 0.157)
0.4 0.094
0.034
(0.028, 0.161)
1.0
0.095
0.035 (0.026, 0.163)
(c)
For
Table
3
-0.4
0.278 0.007
(0.265, 0.292)
0.0
0.363 0.008
(0.347, 0.379)
0.4 0.408
0.009
(0.390, 0.425)
1.0
0.435 0.009
(0.417, 0.453)
(d)
For
Table
4
-0.4
0.432 0.019
(0.395, 0.470)
0.0 0.503 0.020
(0.463, 0.543)
0.4
0.524 0.021
(0.484, 0.565)
1.0 0.530 0.021
(0.488, 0.572)
(e)
For
Table
5
-0.4 0.470 0.010
(0.450, 0.490)
0.0 0.574
0.010
(0.554, 0.593)
0.4 0.622 0.010 (0.603, 0.641)
1.0 0.650 0.009
(0.631, 0.668)
(f)
For
Table
6
-0.4 0.518 0.019 (0.481, 0.554)
0.0 0.624 0.019
(0.587, 0.662)
0.4 0.673 0.019
(0.636,0.710)
1.0 0.699 0.019 (0.663, 0.736)
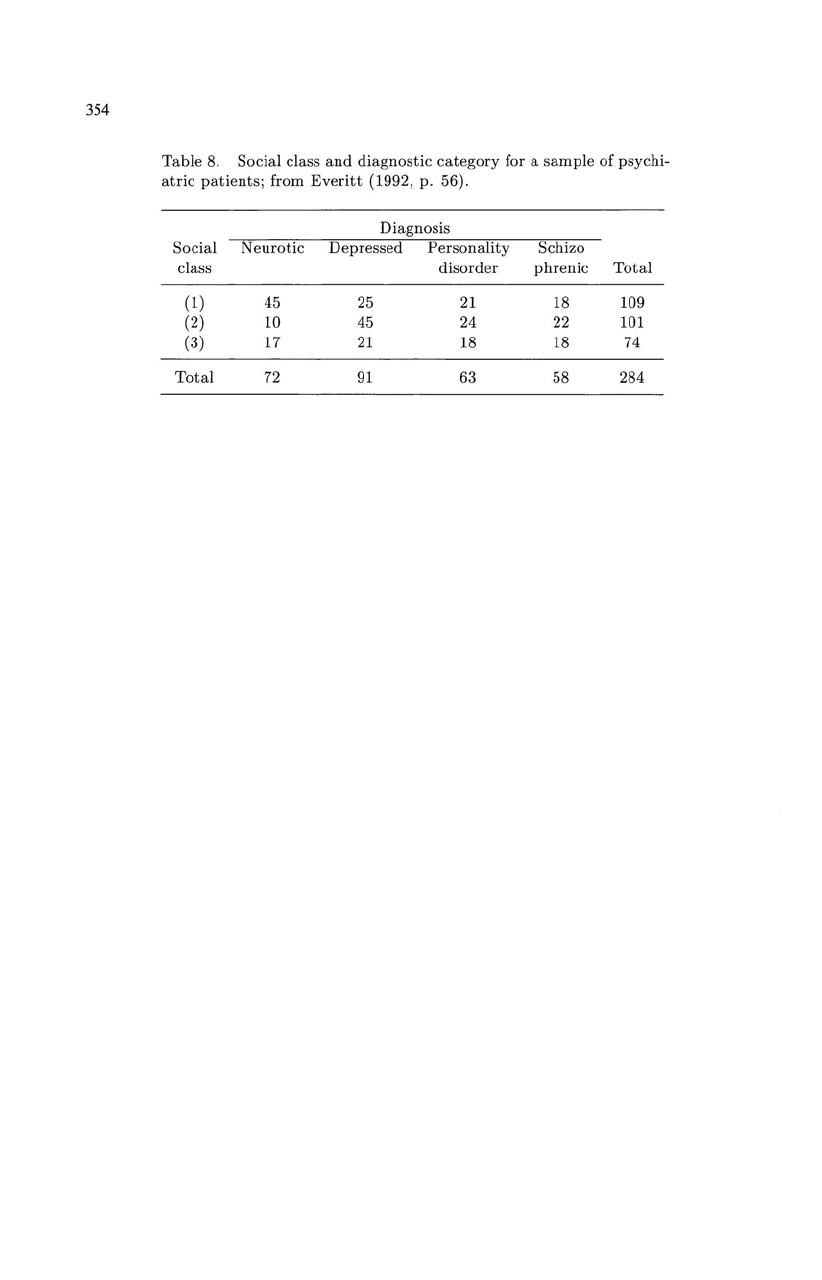
354
Table
8.
Social
class
and
diagnostic
category
for a
sample
of
psychi-
atric
patients;
from
Everitt
(1992,
p.
56).
Diagnosis
Social
Neurotic
Depressed
Personality
Schizo
class
disorder
phrenic
Total
(1) 45 25
21
18 109
(2) 10 45 24 22 101
(3)
17
21
18 18
74
Total
72 91
63 58
284

Quantum
Bio-Informatics
IV
eds. L.
Accardi,
W.
Freudenberg
and
M.
Ohya
© 2011
World
Scientific
Publishing
Co. (pp. 355- 361)
THE
ELECTRON
RESERVOIR
HYPOTHESIS
FOR
TWO-DIMENSIONAL
ELECTRON
SYSTEMS
K.
YAMADA1, T. UCHIDA1 ,
M.
FUJITAl,
H.
KOIZUMI
2
AND
T.
TOYODA
h
1 Department
of
Physic
s,
Tokai University,
Kitakaname
1117, Hiratsuka, Kanagawa 259-1292, Japan
2Nippon Gear
Co., Ltd., Kirihara-cho
7,
Fujisawa, Kanagawa 252-0811, Japan
* Corresponding author. E-mail: toyoda@keyaki.cc.u-tokai.ac.jp
The
el
ectron
reservoir
model
for
the
int
eger
quantum
Hall
effects,
the
magneto-
plasmon
dispersion
plateaus
,
and
the
radiation-induced
magnetoresistance
oscilla-
tions,
are
briefly reviewed.
Keywords:
Two-dimensional
electron
systems;
Quantum
Hall effects;
Magne-
toplasmon
dispersion
;
Magnetoresistance
oscillations.
1.
Introduction
The
quantum
statistical
theory
of
many-electron
systems
is
based
on
the
grand
canonical ensemble, which requires
the
existence
of
an
electron reser-
voir.
If
the
number
of electrons of
the
system
under
consideration is fixed,
then
it
is necessary
to
calculate
the
chemical
potential
as a function
of
the
electron
number
N
exp
and
other
thermodynamic
variables by solving
the
equation
(1)
where
~
oR
is
the
second
quantized
field
operator
in
the
Heisenberg
picture
describing
the
electrons,
and
a is
the
spin
variable.
The
notation
<
...
>G
stands
for
the
grand
canonical ensemble ex
pectation
value defined as
1 (
~
~
)
(
..
')G
==
-tr{e
-
i3
H-j1.N
...
},
Zo
(2)
355

356
where
Ze
is
the
grand
partition
function,
f3
=
l/kBT,
J-L
is
the
chemical
potential,
and
iI
and
N
are
the
Hamiltonian
and
number
operators
for
the
electrons, respectively.
Except
for
the
zero-temperature
limit
of
an
ideal
electron
gas,
the
above
equation
(1)
cannot
be
solved
to
find
the
chemical
potential
(3)
This difficulty is inherent
in
the grand canonical ensemble formulation
of
quantum many-body theories. However, if
the
system
is
an
open
system
with
respect
to
the
electron
number,
the
situation
is
totally
different. In such
a system,
the
chemical
potential
is one
of
the
independent
thermodynamic
variables
that
are
directly controlled in
the
experiment.
Then
one need
not
solve
the
above
equation.
The
aim
of
this
paper
is
to
show
that
there
exist such cases
in
the
two-dimensional electron
systems
(2DES) in vari-
ous
semiconductors
such
as
MOSFET
and
GaAs
heterostructure
FET
1
,2,3.
Three
prominent
cases, i.e.,
the
integer
quantum
Hall effects,
the
magneto-
plasmon
dispersion
plateaus,
and
the
radiation-induced
magnetoresistance
oscillations,
are
briefly reviewed
in
the
following sections.
2.
Quantum
Hall
Effects
In 1980 von Klitzing4 discovered
that
the
Hall
conductivity
of
a two-
dimensional
electron
system
in
the
inversion layer
of
MOSFET
at
a very
low
temperature
(T
= 1.5K) is
quantized
(j=1,2
, ... )
(4)
when
the
system
is
subjected
to
a
strong
perpendicular
magnetic
field
(B
=
18.9T). In 1985, Toyoda,
Gudmundsson,
and
Takahashi
3
showed
that
this
phenomenon
can
be
fully explained
by
introducing
the
second
quantized
Schrodinger field
operators
to
describe
the
electrons
and
by
assuming
the
Hamiltonian
(5)
On
the
right-hand
side,
the
first
term
HA is
the
kinetic
energy
with
minimal
coupling
to
the
magnetic
field;
the
second
term
HE,
the
energy
due
to
the
electric field;
the
third
term
H
spin
,
the
coupling
between
the
spin
and
the
magnetic
field;
the
fourth
term
H
e
-
e
,
the
electron-electron interaction;
and
the
fifth
term
H
imp
,
the
effects of
impurities
or
lattice
defects. Using
this

357
Hamiltonian,
the
canonical
equations
of
motion
for
the
currents
Iv = J d
2
r
[-
ien
ljI~(x
)
'8 vljla(X) -
~
Av(
X)ljI~(
X)ljIa(X)]
2m
me
(6)
are
calculated.
Then
taking
the
grand
canonical ensemble average
of
the
equations
and
considering
the
boundary
conditions,
the
Hall
conductivity
formula
Nee
O"H=B
(7)
is
obtained
.
If
the
2DES is
an
open
system
with
respect
to
electrons,
then
eB
00
1
N = - L L = N((3
fl)
he a n=
al+exp(3(Ena-fl)
"
(8)
where
Ena
is
the
energy
spectrum
of
the
electron
asymptotic
field, i.e.,
the
Landau
levels
with
renormalized
param
ete
rs.
Equations
(7)
and
(8) yield
the
quantum
Hall conductivity formula
e
2
00
1
O"H
= h
~
~
1 + exp
(3
(Ena
-
fl)
.
(9)
The
significance
of
this
result
is
that
the
electron-electron
interaction
and
the
impurity
term
in
the
Hamiltonian
do
not
appear
explicitly.
Their
effects
should
be
in
the
energy
spectrum
Ena.
Adopting
the
linear model for
the
relation b
et
ween
the
chemical
potential
and
the
gate
voltage
fl
= a(Vg +
Va)
(10)
and
assuming
the
Landau
level energy
spectrum
eB
(1)
g*
flB
Ena
=
n--
n + - +
sgn(a)-2-B
,
m*e
2
(11)
where
flB
is
the
Bohr
magneton,
m*
and
g*
are
the
effective mass
and
effective g-factor, respectively,
the
Hall
conductivity
can
be
writt
en as a
function
of
B,
V
g
,
and
temperature.
The
obtained
theoretical
results show
excellent
quantitative
agreement
with
the
experimental
data
3
.
3.
Magnetoplasmon
Dispersion
Plateaus
In
2004, Holland et
al.
6
measured
the
explicit filling factor dependence
of
the
dispersion
of
the
long-wavelength
magnetoplasmon
in
a high-mobility
2DES realized
in
a
GaAs
quantum
well, using
th
e coupling between
the

358
plasmon
with
THz
radiation.
The
observed dispersion seemed
to
deviate
violently from
the
well-established semi-classical dispersion
2 2
271"e
2
N
2
DES
W
mp
=
We
+
q,
em
(12)
where
e is
the
dielectric
constant
of
GaAs semiconductor
into
which
the
2DES is embedded, m is
the
electron effective mass,
-e
is
the
electron
charge,
N
2DE
S is
the
electron
number
density, q is
the
wave-number vector,
and
We
= e
Bjmc
is
the
cyclotron frequency.
U sing
the
measured
magnetoplasmon
frequency
w!;P,
they
defined
the
renormalized
magnetoplasmon
frequency,
{
EXp
}2
2
n
EXP
= W
mp
-
We
mp
We
.
They
plotted
this
n!;P
versus
the
filling factor defined as
hcNsample
v =
---"--
eB
'
(13)
(14)
where
Ns
ample
is
the
electron
number
density
of
the
samples, whose explicit
values were given for
three
samples
in
Ref.
6.
By
substituting
Eqs. (12)
and
(14)
into
Eq. (13),
and
assuming N
2DE
S =
Nsample,
one straightforwardly
finds
n
EXP
_
271"ecNsample
_
271"e
2
mp
-
eB
q -
eh
vq.
(15)
For a fixed value
of
th
e wave-number vector
q,
this
Eq. (15) shows
that
n!;p
is simply
proportional
to
the
filling factor. After
the
measur
eme
nt,
however,
they
found
an
astonishing deviation from such a simple linear
relation.
They
found a
quantized
dispersion
with
plateaus
forming
around
even filling factors.
If
we
follow carefully
the
quantum
statistical
mechanical derivation of
the
dispersion relation (12)10,
then
we find
that
the
quantity
N
2DES
in
the
formula is
actually
the
grand
canonical ensemble
expectation
value for
the
electron
number
density in
the
system
and
that
it
should
be
given by (8).
Then,
the
renormalized
magnetoplasmon
frequency defined by Eq. (13)
should
be
replaced by
271"ecN
2DE
s
eB
q,
(16)
where
w
mp
is given by Eq. (12).
The
only difference between Eqs. (15)
and
(16) is
the
electron
number
density. In Eq. (15),
Nsample
is a given

359
quantity.
On
the
other
hand,
in Eq. (16), N
2DE
S is a function of
the
temperature
T,
the
magnetic
field
strength
B,
and
the
chemical
potential
/-i,
as given by Eq. (8).
Substituting
Eq. (8)
into
Eq. (16), we find
7
Apart
from
the
factor 27rq/c,
the
resemblance
to
the
quantum
Hall conduc-
tivity
formula is derived
in
Refs. 2
and
8 is unmistakable.
This
result (17)
shows excellent agreement
with
the
experimental
data.
4.
Radiation-induced
Magnetoresistance
Oscillations
In
2004, Zudov
et
alY
and
Mani
et
aP2
found a new class
of
magne-
toresistance oscillations in a high-mobility two-dimensional electron
system
(2DES)
in
a
GaAs/
AlxGal-xAs
heterostructure
subjected
to
weak mag-
netic fields
and
millimeterwave radiation.
The
period
of
these
new oscilla-
tions is gove
rned
by
the
ratio
of
the
millimeterwave
to
cyclotron frequen-
cies,
and
the
minima
of
the
oscillations
are
characterized by
an
exponen-
tially vanishing diagonal resistance.
When
the
millimeterwave
radiation
is
turned
off,
the
magnetoresistance shows
the
well-established SdHvA oscil-
lation whose
period
is governed by
the
ratio
of
the
chemical
potential
to
the
cyclotron frequency. Hence
this
magnetoresistance oscillation is
apparently
induced by
the
illumination
with
millimeterwaves.
Although
various dif-
ferent theoretical models have
been
proposed, one crucial question remains
to
be
solved.
The
experiment
by
Smet
et
al.
13
shows
that
the
resistance
oscillations
are
notably
immune
to
the
polarization
of
the
radiation
field.
This
observation is discrepant
with
these
theories
and
seems
to
cast
doubt
on
the
validity
of
the
theoretical models so far proposed.
The
Fermi liquid
theory
of
electrical
conductivity
was originally formu-
lated
by Eliashberg.
The
core
of
the
theory
is
the
analytic
continuation
of
the
finite
temperature
current
correlation function
with
respect
to
the
Mat-
subara
frequency
to
obtain
the
retarded
real-time
current
response function,
which directly yields
the
conductivity. Here
the
formulation given in Ref.
5
is applied
to
an
electron gas
that
is confined
in
the
xy-plane
and
subjected
to
a
perpendicular
magnetic
field B =
(0,0,
B).
The
general expression
of
