Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию
Подождите немного. Документ загружается.

для которых длина перпендикуляра, опущенного из точки на прямую ,
меньше
r и больше r, должны быть окрашены в разные цвета.
863. Пусть дана система линейных неравенств
.0
.......
0
0
222
111
≥++
≥++
≥++
mmm
cybxa
cybxa
cybxa
Каждое из неравенств этой системы определяет в координатной
плоскости некоторую полуплоскость. Если какие- либо числа
х и у
удовлетворяют всем неравенствам системы, то точка (
х, у)
принадлежит пересечению у казанных полуплоскостей. Граница этого
пересечения может состоять из отрезков, полупрямых и целых прямых.
В том случае, когда граница состоит только из отрезков, пересечение
полуплоскостей является выпуклым многоугольником (мы здесь
называем многоугольником не только границу, но и все множество
точек, охваченное границей). Обратно, любой выпуклый
многоугольник, принадлежащий координатной плоскости, может быть
описан системой линейных неравенств. Пусть
n
AA ...,,
1
-
последовательные вершины выпуклого многоугольника, из которых
никакие три не лежат на одной прямой. Можно выписать уравнение
0
111
=++ cybxa прямой, проходящей через точки
21
,AA . Так как
многоугольник выпуклый, то все
n
AAAA ...,,,,
321
лежат в одной
полуплоскости относительно этой прямой. Поэтому в качестве первого
неравенства можно взять
0
111
≥++ cybxa или 0
111
≥−−− cybxa
в зависимости от того, является или нет положительным числом
результат подстановки в
111
cybxa ++ координат какой-либо из точек
n
AAA ...,,,
43
. Аналогичным образом следует поступать с уравнениями
прямых, проходящих через точки
32
, AA и т. д. (последние две точки -
1
, AA
n
).
Даны натуральные числа
n, a
0
,..., a
2n -1
. Пары чисел
1
,
+ii
aa (i
кратно 2) являются координатами точек. Рассматривается граница
l
выпуклого многоугольника с вершинами в точках (36, 30), (30, 27), (24,
30), (З0, 39). Построить
l, а также точки, заданные
последовательностью
a
0
,..., a
2n -1
:
а) лежащие вне многоугольника;
б) лежащие внутри многоугольника, но не на
l;
в) принадлежащие
l (точки выделить цветом, отличным от цвета
l).
г) лежащие где-либо на плоскости; те точки, которые лежат
внутри многоугольника, на его границе и вне его, должны иметь
разные цвета, ни один из которых не совпадает с цветом границы.
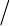
864. Пусть две точки заданы своими координатами ),(
11
yx и
),(
22
yx . Прямая, проходящая через эти две точки может быть описана
следующими параметрическими уравнениями:
tyyyytxxxx )(,)(
121121
−+=−+= .
При 0 <
t < 1 точка (x, y) лежит внутри отрезка и делит его в
отношении
t /(1 - t); при t = 0 достигается конец отрезка ),(
11
yx , при t
= 1 - конец ),(
22
yx . При t > 1 точка (x, y) лежит на прямой вне отрезка
с той же стороны от ),(
11
yx , что и ),(
22
yx ; при t < 0 - с
противоположной стороны.
Даны натуральные числа ,,
11
yx
22
, yx , действительное число
)10( <≤
µ
µ
. Построить отрезок с координатами концов ),(
11
yx ,),(
22
yx
и точку, делящую отрезок в отношении
)1(
µ
µ
− .
865. Начертить узор, показанный на рис. 76. Узор образован 20
вложенными квадратами. Стороны первого квадрата параллельны осям
координат экрана и равны 60. Вершины каждого последующего
квадрата - это точки на сторонах предыду щего квадрата, делящие эти
стороны в отношении
08.0=
µ
(см. предыдущую задачу).
Рис. 76
866. Начертить узор, повторяющий узор, описанный в
предыдущей задаче, но составленный из
а) треугольников;
б) пятиугольников;
в) шестиугольников.
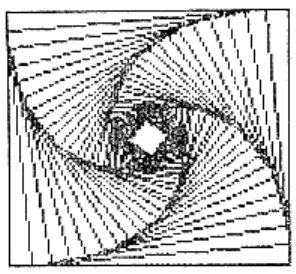
867. Построить узор, показанный на рис. 77, используя
алгоритм описанный в задаче 864
.
Рис. 77
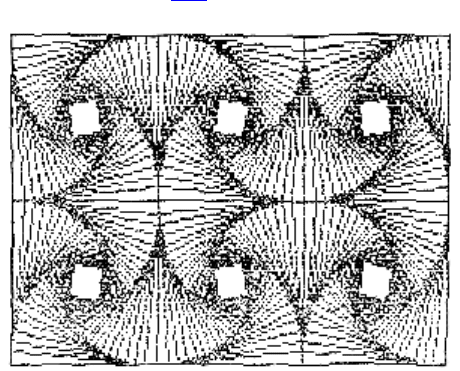
868. Даны натуральные числа x
1
, y
1
, x
2
, y
2
. Начертить штриховые
линии между точками (
x
1
, y
1
) и (x
2
, y
2
) так, как показано на рис. 78.
Способ определения координат точки, лежащей на отрезке с
концами (
x
1
, y
1
) и (x
2
, y
2
) и делящей отрезок в заданном отношении, см.
в задаче 864
.
869. Даны натуральные числа х
1
, у
1
, х
2
, у
2
, х
3
, у
3
, х
4
, у
4.
Построить
две прямые, одна из которых проходит через точки с координатами (
x
1
,
y
1
) и (x
2
, y
2
) а другая - через точки с координатами (x
1
, y
1
) и (x
2
, y
2
).
Построить точку пересечения этих прямых, если она существует, и
Рис. 78 Рис. 79

определить, лежит ли точка пересечения внутри отрезков с концами
(
x
1
, y
1
), (x
2
, y
2
) и (x
3
, y
3
), (x
4
, y
4
) или вне их (см. задачу 864).
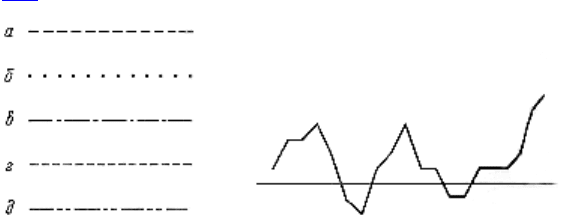
870. Даны целые числа t
1
, t
2
, ..., t
31
. Последовательность
значений
t
1
, t
2
, ..., t
31
задает график температу р за март месяц,
подобный показанному на рис. 79. Построить график температур.
Отрезки прямых, лежащие выше горизонтальной прямой,
соответствующей нулевой температуре, и лежащие ниже этой прямой,
должны быть окрашены в разные цвета.
871. Даны натуральные числа х
1
, у
1
, х
2
, у
2
, х
3
, у
3
. Построить
отрезок с координатами концов (
x
1
, y
1
) и (x
2
, y
2
), а также отрезок,
параллельный и равный по длине первому отрезку; один конец отрезка
должен иметь координаты (
x
3
, y
3
), второй следует расположить:
а) по ту же сторону от (
x
3
, y
3
), что и (x
2
, y
2
) от (x
1
, y
1
);
б) с противоположной стороны.

Воспользоваться тем, что параметрические уравнения прямой,
проходящей через точку (
x
3
, y
3
) и параллельной прямой, проходящей
через точки (
x
1
, y
1
) и (x
2
, y
2
), могут иметь вид
x = x
3
+ (x
2
- x
1
) t, y = y
3
+ (y
2
- y
1
) t.
Координаты конца искомого отрезка вычисляются под-
становкой значений
t= 1 и t= -1. При t= 1 конец отрезка будет
расположен на прямой с той же стороны от (
x
3
, y
3
), что и точка (x
2
, y
2
)
от точки (x
1
, y
1
); при t= -1 с противоположной.
872. Даны натуральные числа х
1
, у
1
, х
2
, у
2
, х
3
, у
3
. Построить
отрезок с координатами концов (
x
1
, y
1
) и (x
2
, y
2
).Через точку (x
3
, y
3
)
провести отрезок, параллельный и равный по длине первому отрезку,
таким образом, чтобы точка (
x
3
, y
3
) делила искомый отрезок пополам
(см. предыдущую задачу и задачу 864
).
873. Даны натуральные числа x
c
, y
c
, h, w, x, y. Построить
прямоугольник с центром в точке (
x
c
, у
c
), высотой h и шириной w, а
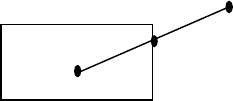
также отрезок прямой с координатами концов (x
c
, у
c
) и (x, y). Отметить
точку пересечения отрезка со стороной прямоугольника (рис. 80).
(
x, y)
),(
cc
yx
Рис. 80
874. Даны натуральные числа x
c
, y
c
, h, w, x, y. Построить
прямоугольник с центром в точке (
x
c
, у
c
), высотой h и шириной w, а
также определить координаты
х
p
, y
p
точки пересечения с
прямоугольником невидимой прямой, проходящей через точки (
x
c
, у
c
)
и (
x, y) (см. предыдущую задачу). Кроме того, построить:
а) отрезок прямой с координатами концов (
x
c
, у
c
) и (x
p
, у
p
) (рис.
81,
а);
б) отрезок прямой с координатами концов (
x, у) и (x
p
, у
p
) (рис.
81,
б).
