Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию
Подождите немного. Документ загружается.


треугольной матрице (см. задачу 716). Кроме этой последовательности
дан вектор
b с n элементами. Найти вектор Аb.
719. Симметричные квадратные матрицы А и В порядка n
заданы последовательностями из
2/)1( +nn чисел, аналогично правым
треугольным матрицам (см. задачу 716
). Получить в аналогичном виде:
а) матрицу
АВ;
б) матрицу
22
B
A − .
§ 22. Численные методы *)
*) С численными методами, рассматриваемыми в задачах этого
раздела, можно ознакомиться в [10].
720.Даны действительные числа
mnn
ttyyxx , , , , , ,, ,
111
KKK
) , ,1 , ,(
121
mixtxxxx
nin
KK =≤≤<<< . Число y представляет
собой значение некоторой функции f от аргумента; )(
jj
xfy =
) , ,1( nj K= . С помощью линейной интерполяции получить значения
f(t
1
), f(t
2
), …, f(t
т
).
721. Даны действительные числа h, x
1
, …, x
n
, y
1
, …, y
n
. Все
сказанное о x
1
, …, x
n
, y
1
, …, y
n
в предыдущей задаче остается в силе. С
помощью линейной интерполяции получить значения функции f для
значений аргументов, равных x
1
, x
1
+h, x
1
+2h, ..., x
1
+kh, где k -
наибольшее целое, для которого x
1
+ kh ≤ x
n
.

722. Даны натуральное число n, действительные числа x
1
, ..., x
n
,
y
1
, ..., y
n
. Рассмотреть предыдущую задачу, считая, что h = (x
n
– x
1
)/n
(ответом должна служить последовательность, содержащая n+1
число).
723. Даны действительные числа x
1
, ..., x
n
, y
1
, ..., y
n
, t (x
1
<x
2
<
...<x
n
, y
1
≤
t ≤y
n
). Предполагается, что y
1
, ...,y
n
представляют собой
результаты измерения температуры воздуха в моменты времени x
1
, ...,
x
n
. С помощью линейной интерполяции указать все моменты времени,
в которые температура воздуха была равна t (не исключен случай
y
j
=y
j+1
=t для некоторых j (1 ≤j ≤n – 1)).
724. Вернуться к задачам 721, 723, считая, что разности между
соседними известными значениями аргумента x
1
, ..., x
n
равны между
собой: x
n
– x
n-1
= x
n-1
–
x
n-2
= ... = x
2
– x
1
= h. Вместо x
1
, ..., x
n
задаются x
1
и
h, порядок остальных исходных данных не изменяется.

725. Дано действительное положительное число
ε
. Методом
деления отрезка пополам найти приближенное значение корня
уравнения f(x) = 0. Абсолютная погрешность найденного значения не
должна превосходить
ε
. (Ниже, рядом с уравнением f(x) = 0,
дополнительно указан отрезок , содержащий корень.)
а) x + ln(x + 0.5) – 0.5 = 0, [0, 2];
б) x
5
– x – 0.2 = 0, [1, 1.1];
в) x
4
+ 2x
3
– x – 1 = 0, [0, 1];
г) x
3
– 0.2x
2
– 0.2x – 1.2 = 0, [1, 1.5];
д)
4
cos3
3
sin2
22
xx
− = 0, [0,
π
/2];
е) x
4
+ 0.8x
3
– 0.4x
2
– 1.4x – 1.2 = 0, [–1.2, –0.5];
ж) x
4
– 4.1x
3
+ x
2
– 5.1x + 4.1 = 0, [3.7, 5].
726. Дано действительное положительное число
ε
. Методом
хорд вычислить с точностью
ε
*) корень уравнения f(x) = 0 (ниже,

следом за уравнением f(x) = 0, дополнительно задан отрезок,
содержащий корень):
а) ⋅
x
2
x
– 1 = 0, [0, 1];
б) x
2
– sin 5x = 0, [0.5, 0.6];
в)
3
2sin2
2
x
–
4
2cos3
2
x
= 0, [0,
π
/4];
г) x
3
– 2x
2
+ x – 3 = 0, [2.1, 2.2]
д) (4 + x
2
)(e
x
– e
-x
) = 18, [1.2, 1.3];
е) x
4
+ 0.5x
3
– 4x
2
– 3x – 0.5 = 0, [–1, 0];
ж) x
2
– 1.3 ln( x + 0.5) – 2.8x + 1.15 = 0, [2.1, 2.5].
*) Когда заходит речь о «вычислении с точностью
ε
», следует
иметь в виду, что лишь немногие численные методы, основанные на
построении последовательных приближений x
0
, x
1
, ... к искомому
числу x, гарантируют, подобно методу деления отрезка пополам, что
абсолютная погрешность найденного значения будет меньше
ε
. Будем
считать, что требуемая точность
ε
достигнута, как только получено
такое x
m
(при m > 1), для которого
1−
−
mm
xx <
ε
. В данной задаче
предполагается, что в программе будет реализован именно этот подход
к оценке точности.
727. Вернуться к предыдущей задаче, считая, что построение
приближений к корню уравнения f(x) = 0 следует закончить, когда
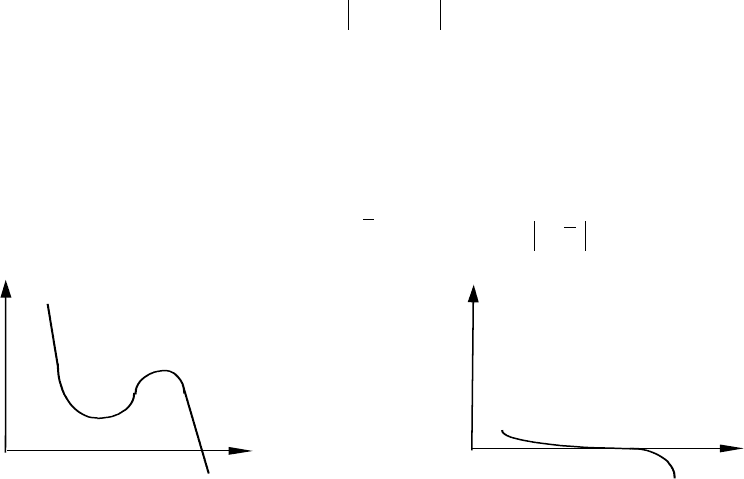
будет получено такое приближение x , для которого )(xf <
ε
. (Этот
а
б
Рис. 41
y
x
y
x

подход к оценке точности может быть приемлемым только в тех
случаях, когда известно, что
)(xf не принимает значений меньше
ε
при значениях
x, удаленных от корня уравнения f(x) = 0; рис.41, а, б.)
728. В уравнениях, приведенных в задачах 725, 726, вычислить
корень, находящийся в заданном отрезке (отрезок следует за
уравнением), методом деления отрезка пополам и методом хорд с
одной и той же точностью
ε
. Сравнить количество шагов, которые
нужно сделать для получения корня этими методами.
729. Дано действительное положительное
ε
. Методом
касательных вычислить с точностью
ε
(см. замечание к № 726) корень
уравнения
f(x) = 0 (ниже, следом за уравнением f(x) = 0, в скобках
указано начальное приближение к корню):
а)
x
3
– 2x
2
+ x – 3 = 0, (2.2);
б) tg
x – x = 0, (4.67);
в) 1.8
x
4
– sin 10x = 0, (0.22);
г) x
4
– 3x
2
+ 75x – 10000 = 0, (–11);
д)
x
3
– 6x
2
+ 20 = 0, (2.31).
730. Решить методом касательных перечисленные в
предыдущей задаче уравнения, прекращая построение приближений к
корню уравнения
f(x) = 0 в тот момент, когда будет получено такое
приближение
x , для которого )(xf < 0.00001.
731. Дано действительное положительное число
ε
. Методом
итераций вычислить с точностью
ε
(см. замечание к № 726) корень
уравнения
f(x) = 0 (ниже, следом за уравнением f(x) = 0, в скобках
указано начальное приближение к корню):
а)
2
sin x
x −
– 1 = 0, (0);
б) 2
x
3
+ 4x – 1 = 0, (0.11);
в)
x
3
+ 12x – 2 = 0, (0.95);
г) 5
x – 8 ln x = 8, (4.32);

д) x
3
+ x = 1000, (9.42);
е)
x – sin x = 0.25, (1.17);
ж)
x
3
– 6x
2
+ 20 = 0, (2.25);
з) 5
x
3
+ 10 x
2
+ 5x – 1 = 0, (0.6).
732. Сравнить методы деления отрезка пополам, хорд,
касательных и итераций, поочередно используя их для решения одного
и того же уравнения. Независимо от метода построение приближений к
корню уравнения
f(x) = 0 следует заканчивать, как только будет
получено такое приближение
x , для которого )(xf <
ε
. Значение
ε
следует поочередно брать равным 0.01, 0.001, ..., 0.0000001. Для
каждого из методов построить график или столбчатую диаграмму
изменения числа потребовавшихся приближений при переходе от
одного значения
ε
к другому. В качестве уравнения, на котором
проводится сравнение методов, и отрезка, которому принадлежит
корень, следует взять:
а)
x
3
+ x
2
– 3 = 0, [0.6, 1.4];
б)
x
5
– x – 0.2 = 0, [0.9, 1.1];
в) 5
x
3
– x – 1 = 0, [0.6, 0.8];
г)
x
3
– 2x – 5 = 0, [1.9, 2.93];
д)
x
3
+ x = 1000, [9.1, 10];
е)
x
4
+ 2x
3
– x – 1 = 0, [0, 1].
Для метода касательных и итераций в качестве начального
приближения выбирается подходящий конец отрезка.
733. Дано действительное положительное число
ε
. Найти с
помощью подходящих методов все корни уравнения
f(x) = 0 с
точностью
ε
. Для получения отрезков, содержащих по одному корню
уравнения
f(x), или для получения начальных приближений к корням
исследовать график функции
y = f(x). В качестве f(x) рассмотреть:
