Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию
Подождите немного. Документ загружается.


соответствующую квадратную матрицу порядка n (элементы главной
диагонали заполняются нулями).
696. Имеется таблица футбольного чемпионата, в котором
участвовало n команд (см. задачу 413). Таблица представлена
целочисленной квадратной матрицей порядка n, элементы главной
диагонали этой матрицы равны нулю. Перестроить эту таблицу,
присвоив каждой команде номер, равный занятому ею месту (для
простоты считается, что при равном числе очков места распределяются
произвольно). Отдельно указать распределение команд в старой
нумерации по занятым ими местам.

§ 21. Матричная алгебра *)
*) В матричной алгебре [10] принято обозначать матрицу какой-нибудь
большой буквой латинского алфавита, а элемент матрицы–
одноименной малой буквой с индексами. Такая система обозначений
выдержана и в этом разделе книги.
За исключением задачи 714, во всех задачах матрицы и векторы
считаются действительными.
697. Даны матрицы А и В размера k×m и m×l соответственно.
Найти произведение АВ.
698. Дана квадратная матрица прядка n. Получить матрицу А
2
.
699. Даны квадратные матрицы А и В порядка n. Получить
матрицу АВ–ВА.
700. Дана квадратная матрица А порядка n. Получить матрицу
АВ; элементы матрицы В вычисляются по формуле:
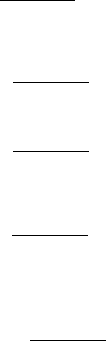
а)
1
1
−+
=
ji
b
ij
;
б)
++
≤
−+
=
случае; противном в
1
1
, если ,
1
1
ji
ji
ji
b
ij
в)
−+
−
=
<
−+
=
случаях остальных в
1
1
, если ,0
, если ,
1
1
ji
ji
ji
ji
b
ij
(i, j=1, …, n).
701. Даны квадратная матрица A порядка n и вектор b c n
элементами. Получить вектор:
а) Ab;
б) A
2
b;
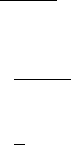
в) (A–E)b, где E–единичная матрица порядка n.
702. Дана квадратная матрица порядка n. Получить вектор Ab,
где b–вектор, элементы которого вычисляются по формуле:
а)
2
1
2
+
=
i
b
i
;
б)
+
=
случае противном в
1
четное, - если ,
2
1
2
i
i
i
b
i
(i=1, …, n).
703. Даны квадратная матрица А порядка n, векторы x и y с n
элементами. Получить вектор A(x+y).
704. Даны квадратные матрицы A, B и C порядка n. Получить
матрицу (A+B)C.

705. Даны квадратные матрицы A и B порядка n. Получить
матрицу A(B–E)+C, где E–единичная матрица порядка n, а элементы
матрицы C вычисляются по формул е
. ..., ,2 ,1 , ,
1
nji
ji
C
ij
=
+
=
706. Пусть даны квадратная матрица A порядка m и натуральное
число n; требуется найти A
n
. Алгоритм, основанный на
непосредственном применении формулы
n
A = AAA ...⋅ (n
сомножителей), слишком разорителен . Например, А
4
экономичнее
вычислять как (А
2
)
2
. Идея одного достаточно экономного алгоритма
вычисления А
п
заключена в следующем: если kn 2= , то
kn
AA )(
2
= ;
если же 12 += kn , то AAA
kn
⋅= )(
2
. Степень с показателем k
вычисляется с учетом этих же соображений. Итак, надо разделить n на
2 с остатком: 1)(0 2 ≤≤+= llkn , потом это же проделать с k и т. д.
Эти действия приводят, как известно, к построению двоичной записи
n. Алгоритм, основанный на этой идее, состоит в том, что
последовательно вычисляются
011010
...
..,., ,
aaaaaaa
ll
AAA
−
, где
011
... aaaa
ll −
–
двоичная запись числа n. Для этого вычисляется, цифра за цифрой,
двоичная запись n и, параллельно, степень за степенью,
..., , ,
)2()2()2(
210
AAA – каждая следующая степень получается из
предыдущей возведением в квадрат. Подсчитывается произведение тех
из вычисленных степеней, для которых соответствующая цифра
двоичного представления равна 1. Например, запись 9 в двоичной
системе есть 1001
)12040819( +⋅+⋅+⋅= ; для вычисления А
9
достаточно найти А
2
, А
4
, А
8
(3 умножения), а затем определить
8
AA⋅ (1
умножение).
Преимущество этого алгоритма в сравнении с простейшим
состоит в том, что простейший алгоритм требует числа умножений,

расту щего как линейная функция от n, а здесь число умножений, грубо
говоря, пропорционально количеству цифр числа n или двоичному
логарифму n. Это преимущество весьма ощутимо при работе с
матрицами (из-за трудоемкости каждого умножения), хотя, разумеется,
этот алгоритм может быть использован и для вычисления степени
любого числа.
Написать программу, реализующую предложенный алгоритм.
707. Дана квадратная матрица порядка 5. Получить матрицу А
15
(см. задачу 706
).
708. Даны квадратная матрица А порядка m, натуральное число
n. Получить матрицу
n
AAAE ++++ ...
2
, где E–единичная матрица
порядка m.
709. Даны квадратная матрица А порядка m, натуральное число
n, действительные числа p
n
, p
n-1
, …, p
0
. Получить матрицу

EpApApAp
n
n
n
n 01
1
1
... ++++
−
−
, где Е – единичная матрица порядка m.
710. Дана матрица А размера nm × . Получить
транспонированную матрицу
А
*
(ее размер – nm × ).
711. Дана матрица А:
а) размера
mm × ;
б) размера
nm × .
Получить матрицу
АА
*
(ее размер mm × ).
712. Дана квадратная матрица А порядка m. Получить матрицы
*)(
2
1
AA +
и *)(
2
1
AA −
.
713. Следом квадратной матрицы называется сумма элементов,
расположенных на главной диагонали.
Даны квадратная матрица порядка
m, натуральное число n.
Вычислить следы матриц
А, А
2
, …, А
n
.
714. Комплексная матрица Z представляется парой X, Y
действительных матриц так, что
iYXZ += . Даны действительные
квадратные матрицы
А, В, С и D порядка m. Найти произведение двух
комплексных матриц
iBA + и iDC + , т . е. найти действительные
квадратные матрицы
X и Y порядка m такие, что
))(( iDCiBAiYX ++=+ .
715. Пусть для квадратной матрицы А, имеющей порядок n,
существу ет обратная матрица
А
-1
. Тогда, рассматривая элементы
матрицы
А
-1
ка неизвестные величины, из соотношения AА
-1
=Е, где Е–
единичная матрица порядка
n, можно получить систему n
2
линейных
уравнений с
n
2
неизвестными. Найти матрицу этой системы и вектор,
определяющий ее правую часть, считая, что неизвестные элементы
матрицы
А
-1
пронумерованы так, что сначала по порядку идут
элементы первой строки, затем–второй, и т. д. Считать, что
А –
заданная матрица порядка 4; в ответе должны получиться квадратная
матрица и вектор порядка 16.
716. Правая треугольная матрица А порядка n задана в виде
последовательности
2/)1( nn + чисел: сначала идет n элементов первой
строки, затем
1−n элемент второй строки, начиная со второго
элемента, и т. д. (из последней,
n–й строки берется только n–й
элемент). Кроме этой последовательности дан вектор
b с n элементами.
Найти вектор
Аb.
717. Две правые треугольные матрицы А и В порядка n заданы
так, как описано в предыдущей задаче. Получить в аналогичном виде:
а) матрицу
АВ;
б) матрицу
А(Е+В
2
), где Е–единичная матрица порядка n.
718. Симметричная квадратная матрица А порядка n задана
последовательностью
2/)1( +nn чисел, аналогично правой
