Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию
Подождите немного. Документ загружается.


файлов a и b без повторений. Файл c должен быть упорядочен по
возрастанию.
656. Дан файл f, компоненты которого являются целыми
числами. Получить в файле g все нечетные числа, входящие в файл f.
Числа в файле g должны следовать:
а) в порядке невозрастания;
б) в порядке убывания, без повторений.
657. Дан символьный файл f, компоненты которого - малые
латинские буквы и пробелы. Слова (см. задачу 269) файла f имеют не
более шестнадцати букв. Записать эти слова в файл g в
лексикографическом порядке.
§19. Многочлены *)
*) Каждый раз, когда в задачах этого раздела говориться, что дан
многочлен P(x) степени n, то подразумевается, что даны
действительные числа (коэффициенты)
n
ppp ...,,,
21
такие, что P(x)=
0
1
1
... pxpxp
n
n
n
n
+++
−
−
. Аналогично, получить многочлен – это значит
получить последовательность его коэффициентов.
658. Дан многочлен P(x) степени n. Получить многочлен P
2
(x).
659. Дан многочлен P(x) степени n. Получить многочлен P(x+1)
- P(x). (Какова степень этого многочлена?).
660. Дан многочлен P(x) степени n. Получить его производную
)(xP
′
, а также вычислить )3(),2(),1( PPP
′′′
661. Даны действительное число a, многочлен P(x) степени n.
Получить
а) многочлен (х – а)P(x);
б) многочлен (х
2
+2ах+3)P(x);
в) многочлен (х
2
+ а
2
)P(x).
662. Даны действительные числа s и t, натуральное число n,
действительные числа a
0
, …, a
n
. Среди а
1
, …, a
n
есть как
отрицательные, так и неотрицательные числа. Получить значение
P(s)+Q(t), где в качестве коэффициентов многочлена P взяты
отрицательные члены последовательности а
0
, …, a
n
(с сохранением
порядка их следования), а в качестве коэффициентов многочлена Q –
неотрицательные члены (также с сохранением порядка их следования).
663. Даны действительные числа s, t, многочлен P(x) степени n.
Найти значение
∫
t
s
dxxP )(.
664. Даны действительные числа s, t, многочлен P(x) степени n.
Получить многочлен (sх
2
+t)P(x)+ )(xP
′
, где )(xP
′
производная
многочлена P(x).
665. Даны действительные числа
510
...,,, aaa . Получить
многочлен шестой степени ))...()((
510
axaxax −−− .
666. Даны действительные числа
50
...,, aa ,
50
...,, dd . Получить
многочлен шестой степени d
0
+ d
1
(х – а
0
) + d
2
(х – а
0
) (х – а
1
) + … + d
5
(х – а
0
)(х – а
1
)… (х – а
5
).
667. Даны действительные числа
50
...,, aa , многочлен P(x)
шестой степени. Получить действительные числа
70
...,, dd такие, что
P(x)= d
0
+ d
1
(х – а
0
) + + d
2
(х – а
0
) (х – а
1
)+…+ d
7
(х – а
0
) (х – а
1
) … (х –
а
5
).
668. Последовательность многочленов T
0
(x), T
1
(x), …
определяется следующим образом: T
0
(x)=1, T
1
(x)=x, T
k
(x)=2xT
k – 1
(x) –
T
k – 2
(x), (k = 2, 3, …). Получить T
2
(x), …, T
8
(x).
669. Последовательность многочленов H
0
(x), H
1
(x), …
определяется следующим образом: H
0
(x)=1, H
1
(x)=2, H
k
(x)=xH
k – 1
(x) –
(k – 1)H
k – 2
(x) (k = 2, 3, …).
a) Получить H
3
(x), H
5
(x), H
6
(x).
б) Даны действительные числа a
0
, …, a
6
. Получить многочлен
a
0
H
0
(x)+…+a
6
H
6
(x).
в) Дано действительное число a. Вычислить H
0
(a)+…+H
6
(a).
670. Последовательность многочленов G
0
(x), G
1
(x), …
определяется следующим образом: G
0
(x)=1, G
1
(x)= x – 1, G
k
(x) = (x –
2k+1)G
k – 1
(x) – (k – 1)
2
G
k – 2
(x) (k = 2, 3, …). Выполнить для G
0
(x), G
1
(x),
… задания а), б), в), сформулированные в предыдущей задаче для
многочленов H
0
(x), H
1
(x), ….

671. Последовательность многочленов L
0
(x), L
1
(x), …,
определяется следующим образом L
0
(x) =1, L
1
(x) = x,
)(
)12)(32(
)1(
)()(
2
2
1
xL
kk
k
xxLxL
kkk −−
−−
−
−= , k = 2, 3, …
а) Получить L
5
(x), L
7
(x).
б) Даны действительные числа d
0
, …d
8
, a. Вычислить
d
0
+d
1
L
1
(a)+…+d
8
L
8
(a).
в) Получить многочлен L
0
(x)+L
1
(x)+…+L
6
(x).
672. Даны действительные числа a
0
, …, a
n
, b
0,
…, b
n
(a
0
, …, a
n
попарно различны). Требуется найти многочлен F(x) степени не выше,
чем n, такой, что F(a
i
)= b
i
( i = 0, 1, …, n).
Отметим, что нетрудно построить многочлены
)(...,),(),(
10
xwxwxw
n
каждый из которых имеет степень n и которые
обладают тем свойством, что ω
i
(x) равен 1 при x = a
i
и равен 0 при x
= a
0
, a
1
, …, a
i – 1
, a
i+1
, …, a
n
– для этого достаточно положить

))...()(...)...()((
))...()()...()((
)(
1110
1110
niiiiiii
nii
i
aaaaaaaaaa
axaxaxaxax
x
−−−−
−−−−−
=
+−
+−
ω
,
i = 0, 1, …, n.
В качестве искомого многочлена F(x) берется сумма
)(...)()(
1100
xbxbxb
nn
ω
ω
ω
+++ .
§ 20. Преобразование и построение матриц
673. Даны действительная матрица размера n×(n+1),
действительные числа
1111
...,,,...,,
++ nn
bbaa , натуральные числа p, q (p
≤ n, q ≤ n+1). Образовать новую матрицу размера (n+1)×(n+2) вставкой
после строки с номером p данной матрицы новой строки с элементами
a
1
,…, a
n+1
и последующей вставкой после столбца с номером q нового
столбца с элементами b
1
, …, b
n+1
.
674. Даны целые числа a
1
, …, a
10
, целочисленная квадратная
матрица порядка n. Заменить нулями в матрице те элементы с четной
суммой индексов, для которых имеются равные среди a
1
, …, a
10
.
675. Даны действительные числа a
1
, …, a
n
, действительная
квадратная матрица порядка n (n ≥ 6). Получить действительную
матрицу размера n×(n+1), вставив в исходную матрицу между пятым и
шестым столбцами новый столбец с элементами a
1
, …, a
n
.
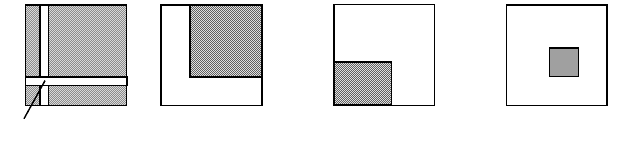
676. Дана целочисленная матрица размера 6×9. Найти матрицу,
получающуюся из данной:
а) перестановкой столбцов – первого с последним, второго с
предпоследним и т. д.;
б) перестановкой строк – первой с последней, второй – с
предпоследней и т.д.
a
ij
a
ij
a
ji
a
ij
a
ij
Рис. 36
677. Дана действительная матрица [ a
ij
]
i,j
=
1, …, n
. Получить
действительную матрицу [ b
ij
]
i,j
=
1, …, n
, элемент b
ij
который равен
сумме элементов данной матрицы, расположенных в области,
определяемой индексами i, j так, как показано на рис. 36, а – г
(область заштрихована).
Сходным образом можно рассмотреть вместо суммы элементов
их произведение, набольшее значение, наименьшее значение.
678. Дана действительная квадратная матрица порядка n.
Преобразовать матрицу по правилу: строку с номером n сделать
столбцом с номером n, а столбец с номером n сделать строкой с
номером n.
679. Даны две действительные квадратные матрицы порядка n.
Получить новую матрицу:
а) умножением элементов каждой строки первой матрицы на
наибольшее из значений элементов соответствующей строки второй
матрицы;
б) прибавлением к элементам каждого столбца первой матрицы
произведения элементов соответствующих строк второй матрицы.
