Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию
Подождите немного. Документ загружается.

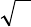
а) x
3
– 6x
2
+ 12x + 5 = 0;
б)
x
6
+ x
2
– 2 = 0;
в)
x
3
+ 3x + 2 = 0;
г)
x + 1 = cos (0.5x);
д) 3
x
2
– cos 2x – 1 = 0;
е) 2ln
x – 1/x + 0.5 = 0;
ж)
x
4
– 6x
3
+ 9x
2
– 16 = 0.
734. Найти с точностью 0.00001 наименьший корень уравнения:
а)
x
3
– 6x
2
+ 19.8 = 0;
б)
x
4
+ x
3
– 10x
2
– 34x – 25 = 0;
в)
x
3
– 1.75x + 0.75 = 0;
г)
x
5
+5x
4
– 2x
3
– 4x
2
+ 7x – 3 = 0;
д) 3
x – sin x = 7;
е)
x
8
– 0.4x
3
– 1.24 = 0;
ж)
x = cos x +1;
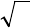
з) e
-x
= 0.5 + x ;
и)
x
4
+ 39x
3
+ 958x
2
– 1081x – 1987 = 0.
Использовать какой-нибудь подходящий численный метод
решения уравнений. Для получения отрезка, содержащего наименьший
корень уравнения
f(x) = 0, или для получения начального приближения
к этому корню исследовать график функции
y = f(x).
735. Вернуться к предыдущей задаче, рассматривая вместо
наименьшего корня:
а) наибольший;
б) наименьший отрицательный;
в) наибольший положительный;
г) второй по величине;
д) наименьший по модулю.
736. Найти с точностью 0.0001 все корни уравнения 1/x = sin x,
принадлежащего отрезку [
π
− ,
π
].

737. Для каждого целого числа n из диапазона от 1 до 50 найти
подходящим методом с точностью 1/
n
2
наибольший корень уравнения
2
2
3
3x
n
x
− + 1 = 0 (этот корень, как нетрудно показать, меньше, чем 3n
2
).
Получить графическое изображение зависимости значения
наибольшего корня от
n.
738. Иногда функция y = f(x) задается на некотором отрезке с
помощью уравнения вида
F(x, y) = 0. Вычислить значения функции,
заданной уравнением:
а)
y
3
+ x
3
– 2xy = 0 для x = 0, –0.1, –0.2, ..., –1;
б)
y
3
+ y
2
– x
2
= 0 для x = 1, 1.1, 1.2, ..., 2.
В первом случае функция определена и неотрицательна на
отрезке [–1, 0], ее значения на этом отрезке меньше, чем 1; во втором
случае функция определена и отрицательна на отрезке [1, 2], ее
значения на этом отрезке меньше, чем 1.5. Для нахождения значений
y
использовать подходящий численный метод решения уравнений.
Вычисление проводить с точностью 0.0001.
739. Написать программу решения по методу Гау сса системы
линейных уравнений
a
11
x
1
+ ... + a
1n
x
n
= b
1
,
. . . . . . . . . . . . . . . . . .
a
n1
x
1
+ ... + a
nn
x
n
= b
n
.
Квадратная матрица [
a
ij
]
i,j = 1, ..., n
и вектор b
1
, ..., b
n
- исходные данные
задачи (предполагается, что система совместна и имеет единственное
решение).
Применить программу для решения следующих систем:
а)
;141022
,13102
,1210
321
321
321
=++
=++
=++
xxx
xxx
xxx
б)
;20408.004.0
,915.0309.0
,808.024.04
321
321
321
=+−
=−+
=−+
xxx
xxx
xxx
в)
;426
,326
,33.116
321
321
321
=+−−
=−+−
=−−
xxx
xxx
xxx
г)
;1542
,02
,53
321
321
21
=+−
=−+−
=−
xxx
xxx
xx
д)
;423.1175.4273.1012.0
,176.0102.1513.0270.4
,425.2307.1210.3427.0
321
321
321
=−+
−=+−
=−+
xxx
xxx
xxx
е)
;152023
,102032
,0210
,03210
4321
4321
432
4321
1
=+++
−=−++
=+−−
=−+−
xxxx
xxxx
xxxx
xxxx
ж)
;07.41.2210
,014315.0
,02521.0
,01.3432
4321
4321
4321
4321
=++−+
=−−+−
=−+−−
=−+−+
xxxx
xxxx
xxxx
xxxx
з)
;1.37.39.33.1
,148.02
,1241.35.0
,64.25.13
4321
421
4321
4321
=−+−
=−−
−=−−+−
=+−+
xxxx
xxx
xxxx
xxxx
и)
;79.242.341.233.487.2
,33.276.014.375.219.0
,16.471.115.023.727.1
,32.061.094.187.213.4
4321
4321
4321
4321
=−−+
=−++
−=+−+
=+−−
xxxx
xxxx
xxxx
xxxx
к)
;3.343232
,5.7352
,522352
,4.53543
,5.0223
54321
5432
54321
54321
5321
=+++−−
=++−
=+−+−−
=−+−+
=−−+
xxxxx
xxxx
xxxxx
xxxxx
xxxx
л)
;13.89.84.12.3
,6.83.92.32.43.4
,95.95.35.08.45.8
,68.62.77.56.59.7
4321
4321
4321
4321
=+−−
=+−+
=++−
=−++
xxxx
xxxx
xxxx
xxxx

м)
.06.3214.871.23.68
,08.2592.46.7928.9
,03.501.907.62.10
321
321
321
=+−−
=+−−
=+−+
xxx
xxx
xxx
740. Дано действительное положительное число ε. Методом
итераций решить систему линейных алгебраических уравнений с
точностью ε. В данной задаче вычисление с точностью ε означает
следующее. Вычисляется последовательность векторов-приближений
() () () ()
),...,(
21
m
n
mmm
xxxx =
где
n—число неизвестных системы, m=0, 1, 2, ...
Если для некоторого
k выполнено условие
,max
)()1(
ε
<−
− k
i
k
i
i
xx i=1, 2, ... , n,
то вектор
),...,,(
)()(
2
)(
1
)( k
n
kkk
xxxx = считается решением системы с
точностью ε:
а)
;02.001.05
,05.003.03
,02.006.02
213
312
321
xxx
xxx
xxx
+−=
+−=
+−=
б)
;2.02.04.1
,1.02.03.1
,1.01.02.1
213
312
321
xxx
xxx
xxx
−−=
−−=
−−=
в)
;75.0005.01.015.0
,5.005.015.01.0
,5.02.01.01.0
,3.02.01.0
3214
4213
4312
4321
+−−−=
−+−−=
+−+−=
+−=
xxxx
xxxx
xxxx
xxxx
г)
;111.1333.0
,4.02.04.02.0
,2.02.02.0
,4.02.01.02.0
14
4213
312
4321
−=
−+−=
+−=
−−+−=
xx
xxxx
xxx
xxxx
д)
;34.109.01.004.0
,26.011.006.015.0
,64.008.018.012.0
3213
3212
3211
+−−=
+−+=
−+−=
xxxx
xxxx
xxxx
е)
;2.01.01.0
,1.01.01.0
,2.01.01.01.0
,3.02.01.0
432
432
4321
321
=++−
=−+−
−=−−+
=+−
xxx
xxx
xxxx
xxx
ж)
.93.138.912.376.1
,4.243.271.972.2
,44.284.124.192.5
321
321
321
=+−
=+−
=−−
xxx
xxx
xxx
741. Вычислить интегралы по формулам численного
интегрирования и по формуле Ньютона-Лейбница. Сравнить
результаты:
