A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику

Подождите немного. Документ загружается.

304 20 Eﬃciency and mean squared error

Remark 20.1 (How to compute this variance). The trick is to com-

pute not E





but E[M

+ 1)]. First we derive an identity from Equa-

tion (20.1) as before, this time replacing N by N +2andn by n +2:

N+2



j=n+2

(j − 1)!

(j − n − 2)!

(N +2)!

(n +2)(N − n)!

Changing the summation variable to k = j − 2 yields



k=n

(k +1)!

(k − n)!

(N +2)!

(n +2)(N − n)!

With this formula one can obtain:

E[M

+1)]=



k=n

k(k +1)· n

(k − 1)!

(k − n)!

(N − n)!

n(N +1)(N +2)

n +2

Since we know E[M

], we can determine E





from this, and subsequently

the variance of M

With the expression for the variance of M

,wederive

Var(T

)=Var



n +1

− 1



(n +1)

Var(M

(N +1)(N − n)

n(n +2)

We see that Var(T

) < Var(T

) for all N and n ≥ 2. Hence T

is always more

eﬃcient than T

, except when n = 1. In this case the variances are equal,

simply because the estimators are the same—they both equal X

The quotient Var(T

) /Var(T

), is called the relative eﬃciency of T

with

respect to T

. In our case the relative eﬃciency of T

with respect to T

equals

Var(T

)

Var(T

)

(N +1)(N − n)

n(n +2)

(N +1)(N − n)

n +2

Surprisingly, this quotient does not depend on N, and we see clearly the

advantage of T

over T

as the sample size n gets larger.

Quick exercise 20.4 Let n = 5, and let the sample be

7 3 10 45 15.

Compute the value of the estimator T

for N. Do you notice anything strange?

The self-contradictory behavior of T

in Quick exercise 20.4 is not rare: this

phenomenon will occur for up to 50% of the samples if n and N are large.

This gives another reason to prefer T

over T

20.3 Mean squared error 305

Remark 20.2 (The Cram´er-Rao inequality). Suppose we have a ran-

dom sample from a continuous distribution with probability density function

,whereθ is the parameter of interest. Under certain smoothness condi-

tions on the density f

, the variance of an unbiased estimator T for θ always

has to be larger than or equal to a certain positive number, the so-called

Cram´er-Rao lower bound:

Var(T ) ≥





∂

∂θ

ln f

(X)





for all θ.

Here n is the size of the sample and X a random variable whose density

function is f

. In some cases we can ﬁnd unbiased estimators attaining this

bound. These are called minimum variance unbiased estimators.Anexam-

ple is the sample mean for the expectation of an exponential distribution.

(We will consider this case in Exercise 20.3.)

20.3 Mean squared error

In the last section we compared two unbiased estimators by considering their

spread around the value to be estimated, where the spread was measured by

the variance. Although unbiasedness is a desirable property, the performance

of an estimator should mainly be judged by the way it spreads around the

parameter θ to be estimated. This leads to the following deﬁnition.

Definition. Let T be an estimator for a parameter θ.Themean

squared error of T is the number MSE(T )=E



(T − θ)



According to this criterion, an estimator T

performs better than an estima-

tor T

if MSE(T

) < MSE(T

). Note that

MSE(T )=E



(T − θ)





(T − E[T ]+E[T ] − θ)





(T − E[T ])



+2E[T − E[T ]] (E [T ] − θ)+(E[T ] − θ)

=Var(T )+(E[T ] − θ)

So the MSE of T turns out to be the variance of T plus the square of the bias

of T . In particular, when T is unbiased, the MSE of T is just the variance

of T . This means that we already used mean squared errors to compare the

estimators T

and T

in the previous section. We extend the notion of eﬃciency

by saying that estimator T

is more eﬃcient than estimator T

(for the same

parameter of interest), if the MSE of T

is smaller than the MSE of T

Unbiasedness and eﬃciency

A biased estimator with a small variance may be more useful than an unbiased

estimator with a large variance. We illustrate this with the network server

306 20 Eﬃciency and mean squared error

−µ

0.2 0.3 0.4

−µ

0.2 0.3 0.4

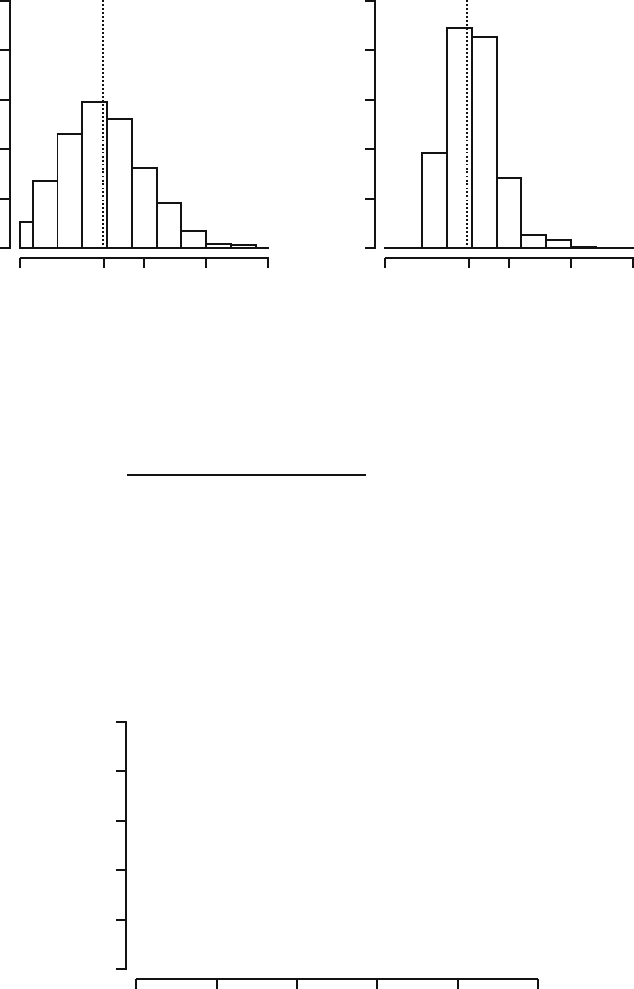
Fig. 20.2. Histograms of a thousand values for S (left) and T (right).

example from Section 19.2. Recall that our goal was to estimate the probability

−µ

of zero arrivals (of packages) in a minute. We did have two promising

candidates as estimators:

S =

number of X

equal to zero

and T =e

−

In Figure 20.2 we depict histograms of one thousand simulations of the values

of S and T computed for random samples of size n =25fromaPois(µ)

distribution, where µ = 2. Considering the way the values of the (biased!)

estimator T are more concentrated around the true value e

−µ

−2

=0.1353,

we would be inclined to prefer T over S. This choice is strongly supported

by the fact that T is more eﬃcient than S:MSE(T ) is always smaller than

MSE(S), as illustrated in Figure 20.3.

012345

0.000

0.002

0.004

0.006

0.008

0.010

MSE(S)



MSE(T )



...

....

...

....

...

....

...

....

..........

....

...

....

...

...........

..........

...

..........

................

....

.....................

..................................

...

............................................

Fig. 20.3. MSEs of S and T as a function of µ.

20.5 Exercises 307

20.4 Solutions to the quick exercises

20.1 We have ¯x

= (61 + 19 + 56 + 24 + 16)/5 = 176/5=35.2. Therefore

=2·35.2 − 1=69.4.

20.2 When n = N,wehavedrawnall the numbers. But then the largest

number M

is N ,andsoE[M

]=N.

20.3 We have t

=(6/5) · 61 − 1=72.2.

20.4 Since 45 is in the sample, N has to be at least 45. Adding the numbers

yields 7 + 3 + 10 + 15 + 45 = 80. So t

=2¯x

− 1=2· 16 − 1=31. What is

strange about this is that the estimate for N is far smaller than the number

45 in the sample!

20.5 Exercises

20.1 Given is a random sample X

,...,X

from a distribution with ﬁnite

variance σ

. We estimate the expectation of the distribution with the sample

mean

. Argue that the larger our sample, the more eﬃcient our estimator.

What is the relative eﬃciency Var





/Var





with respect to

20.2  Given are two estimators S and T for a parameter θ.Furthermoreit

is known that Var(S) = 40 and Var(T )=4.

a. Suppose that we know that E[S]=θ and E[T ]=θ + 3. Which estimator

would you prefer, and why?

b. Suppose that we know that E [S]=θ and E[T ]=θ + a for some positive

number a.Foreacha, which estimator would you prefer, and why?

20.3  Suppose we have a random sample X

,...,X

from an Exp(λ) distri-

bution. Suppose we want to estimate the mean 1/λ. According to Section 19.4

the estimator

+ X

+ ···+ X

)

is an unbiased estimator of 1/λ.LetM

be the minimum of X

,...,X

Recall from Exercise 8.18 that M

has an Exp(nλ) distribution. In Exer-

cise 19.5 you have determined that

= nM

is another unbiased estimator for 1/λ. Which of the estimators T

and T

would you choose for estimating the mean 1/λ? Substantiate your answer.

308 20 Eﬃciency and mean squared error

20.4  Consider the situation of this chapter, where we have to estimate the

parameter N from a sample x

,...,x

drawn without replacement from the

numbers {1,...,N}. To keep it simple, we consider n =2.LetM = M

the maximum of X

and X

. We have found that T

=3M/2 − 1 is a good

unbiased estimator for N. We want to construct a new unbiased estimator

based on the minimum L of X

and X

. In the following you may use

that the random variable L has the same distribution as the random variable

N +1− M (this follows from symmetry considerations).

a. Show that T

=3L − 1isanunbiasedestimatorforN.

b. Compute Var(T

)usingthatVar(M )=(N +1)(N − 2)/18. (The latter

has been computed in Remark 20.1.)

c. What is the relative eﬃciency of T

with respect to T

20.5 Someone is proposing two unbiased estimators U and V ,withthesame

variance Var(U )=Var(V ). It therefore appears that we would not prefer one

estimator over the other. However, we could go for a third estimator, namely

W =(U + V )/2. Note that W is unbiased. To judge the quality of W we

want to compute its variance. Lacking information on the joint probability

distribution of U and V , this is impossible. However, we should prefer W in

any case! To see this, show by means of the variance-of-the-sum rule that the

relative eﬃciency of U with respect to W is equal to

Var((U + V )/2)

Var(U )

ρ(U, V ) .

Here ρ(U, V ) is the correlation coeﬃcient. Why does this result imply that we

should use W instead of U (or V )?

20.6 A geodesic engineer measures the three unknown angles α

,α

, and α

of a triangle. He models the uncertainty in the measurements by considering

them as realizations of three independent random variables T

, and T

with expectations

E[T

]=α

, E[T

]=α

, E[T

]=α

and all three with the same variance σ

. In order to make use of the fact that

the three angles must add to π, he also considers new estimators U

, and

deﬁned by

(π − T

− T

(π − T

− T

(π − T

− T

(Note that the “deviation” π − T

− T

is evenly divided over the three

measurements and that U

+ U

= π.)

20.5 Exercises 309

a. Compute E[U

]andVar(U

) .

b. What does he gain in eﬃciency when he uses U

instead of T

to estimate

the angle α

c. What kind of estimator would you choose for α

if it is known that the

triangle is isosceles (i.e., α

= α

20.7  (Exercise 19.7 continued.) Leaves are divided into four diﬀerent types:

starchy-green, sugary-white, starchy-white, and sugary-green. According to

genetic theory, the types occur with probabilities

(θ +2),

θ,

(1 − θ), and

(1 − θ), respectively, where 0 <θ<1. Suppose one has n leaves. Then the

number of starchy-green leaves is modeled by a random variable N

with a

Bin(n, p

) distribution, where p

(θ + 2), and the number of sugary-white

leaves is modeled by a random variable N

with a Bin (n, p

) distribution,

where p

θ. Consider the following two estimators for θ:

− 2andT

In Exercise 19.7 you showed that both T

and T

are unbiased estimators

for θ. Which estimator would you prefer? Motivate your answer.

20.8  Let

and

be the sample means of two independent random

samples of size n (resp. m) from the same distribution with mean µ.We

combine these two estimators to a new estimator T by putting

T = r

+(1− r)

where r is some number between 0 and 1.

a. Show that T is an unbiased estimator for the mean µ.

b. Show that T is most eﬃcient when r = n/(n + m).

20.9 Given is a random sample X

,...,X

from a Ber(p) distribution.

One considers the estimators

+ ···+ X

)andT

=min{X

,...,X

a. Are T

and T

unbiased estimators for p?

b. Show that

MSE(T

p(1 − p), MSE(T

)=p

− 2p

n+1

+ p

c. Which estimator is more eﬃcient when n =2?

20.10 Suppose we have a random sample X

,...,X

from an Exp(λ) distri-

bution. We want to estimate the expectation 1/λ. According to Section 19.4,

310 20 Eﬃciency and mean squared error

+ X

+ ···+ X

)

is an unbiased estimator of 1/λ. Let us consider more generally estimators T

of the form

T = c · (X

+ X

+ ···+ X

) ,

where c is a real number. We are interested in the MSE of these estimators

and would like to know whether there are choices for c that yield a smaller

MSE than the choice c =1/n.

a. Compute MSE(T )foreachc.

b. For which c does the estimator perform best in the MSE sense? Compare

this to the unbiased estimator

that one obtains for c =1/n.

20.11  In Exercise 17.9 we modeled diameters of black cherry trees with the

linear regression model (without intercept)

= βx

+ U

for i =1, 2,...,n.Asusual,theU

here are independent random variables

with E[U

]=0, and Var(U

)=σ

We considered three estimators for the slope β of the line y = βx:theso-

called least squares estimator T

(which will be considered in Chapter 22),

the average slope estimator T

, and the slope of the averages estimator T

These estimators are deﬁned by:



i=1



i=1



i=1



i=1



i=1

In Exercise 19.8 it was shown that all three estimators are unbiased. Compute

the MSE of all three estimators.

Remark: it can be shown that T

is always more eﬃcient than T

,whichin

turn is more eﬃcient than T

. To prove the ﬁrst inequality one uses a famous

inequality called the Cauchy Schwartz inequality; for the second inequality

one uses Jensen’s inequality (can you see how?).

20.12 Let X

,...,X

represent n draws without replacement from the

numbers 1, 2,...,N with equal probability. The goal of this exercise is to

compute the distribution of M

in a way other than by the combinatorial

analysis we did in this chapter.

a. Compute P(M

≤ k), by using, as in Section 8.4, that:

P(M

≤ k)=P(X

≤ k, X

≤ k,...,X

≤ k) .

20.5 Exercises 311

b. Derive that

P(M

= n)=

n!(N − n)!

c. Show that for k = n +1,...,N

P(M

= k)=n ·

(k − 1)!

(k − n)!

(N −n)!

Maximum likelihood

In previous chapters we could easily construct estimators for various param-

eters of interest because these parameters had a natural sample analogue:

expectation versus sample mean, probabilities versus relative frequencies, etc.

However, in some situations such an analogue does not exist. In this chap-

ter, a general principle to construct estimators is introduced, the so-called

maximum likelihood principle. Maximum likelihood estimators have certain

attractive properties that are discussed in the last section.

21.1 Why a general principle?

In Section 4.4 we modeled the number of cycles up to pregnancy by a ran-

dom variable X with a geometric distribution with (unknown) parameter p.

Weinberg and Gladen studied the eﬀect of smoking on the number of cycles

and obtained the data in Table 21.1 for 100 smokers and 486 nonsmokers.

Table 21.1. Observed numbers of cycles up to pregnancy.

Numberofcycles1 2 3456789101112>12

Smokers 291617439451113 7

Nonsmokers 19810755381822795 3 6 6 12

Source: C.R. Weinberg and B.C. Gladen. The beta-geometric distribution ap-

plied to comparative fecundability studies. Biometrics, 42(3):547–560, 1986.

Is the parameter p, which equals the probability of becoming pregnant after

one cycle, diﬀerent for smokers and nonsmokers? Let us try to ﬁnd out by

estimating p in the two cases.

314 21 Maximum likelihood

What would be reasonable ways to estimate p?Sincep =P(X = 1), the law

of large numbers (see Section 13.3) motivates use of

S =

number of X

equal to 1

as an estimator for p. This yields estimates p =29/100 = 0.29 for smokers and

p = 198/486 = 0.41 for nonsmokers. We know from Section 19.4 that S is an

unbiased estimator for p. However, one cannot escape the feeling that S is a

“bad” estimator: S does not use all the information in the table, i.e., the way

the women are distributed over the numbers 2, 3,... of observed numbers of

cycles is not used. One would like to have an estimator that incorporates all

the available information. Due to the way the data are given, this seems to be

diﬃcult. For instance, estimators based on the average cannot be evaluated,

because 7 smokers and 12 nonsmokers had an unknown number of cycles

up to pregnancy (larger than 12). If one simply ignores the last column in

Table 21.1 as we did in Exercise 17.5, the average can be computed and yields

1/¯x

=0.2809 as an estimate of p for smokers and 1/¯x

474

=0.3688 for

nonsmokers. However, because we discard seven values larger than 12 in case

of the smokers and twelve values larger than 12 in case of the nonsmokers, we

overestimate p in both cases.

In the next section we introduce a general principle to ﬁnd an estimate for a

parameter of interest, the maximum likelihood principle. This principle yields

good estimators and will solve problems such as those stated earlier.

21.2 The maximum likelihood principle

Suppose a dealer of computer chips is oﬀered on the black market two batches

of 10 000 chips each. According to the seller, in one batch about 50% of the

chips are defective, while this percentage is about 10% in the other batch. Our

dealer is only interested in this last batch. Unfortunately the seller cannot tell

the two batches apart. To help him to make up his mind, the seller oﬀers our

dealer one batch, from which he is allowed to select and test 10 chips. After

selecting 10 chips arbitrarily, it turns out that only the second one is defective.

Our dealer at once decides to buy this batch. Is this a wise decision?

With the batch where 50% of the chips are defective it is more likely that

defective chips will appear, whereas with the other batch one would expect

hardly any defective chip. Clearly, our dealer chooses the batch for which it is

most likely that only one chip is defective. This is also the guiding idea behind

the maximum likelihood principle.

The maximum likelihood principle. Given a dataset, choose

the parameter(s) of interest in such a way that the data are most

likely.

A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику - Как? и Почему? )

Подождите немного. Документ загружается.