A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику

Подождите немного. Документ загружается.

18.2 The empirical bootstrap 273



lim

n→∞

sup

t∈R

∗

(t) − G

(t)| =0



(see, for instance, Singh [32]). In fact, the empirical bootstrap approxima-

tion can be improved by approximating the distribution of the standardized

average

√

−µ)/σ by its bootstrapped version

√

∗

−µ

∗

)/σ

∗

,where

σ and σ

∗

denote the standard deviations of F and F

. This approximation

is even better than the normal approximation by the central limit theorem!

See, for instance, Hall [14].

Let us continue with approximating the distribution of

− µ by that of

∗

−µ

∗

. First note that the empirical distribution function F

of the original

dataset is the distribution function of a discrete random variable that attains

the values x

,...,x

, each with probability 1/n. This means that each of

the bootstrap random variables X

∗

has expectation

∗

=E[X

∗

]=x

+ x

+ ···+ x

=¯x

Therefore, applying the empirical bootstrap to

−µ means approximating

its distribution by that of

∗

− ¯x

. In principle it would be possible to deter-

mine the probability distribution of

∗

−¯x

. Indeed, the random variable

∗

is based on the random variables X

∗

, whose distribution we know precisely:

it takes values x

,...,x

with equal probability 1/n. Hence we could de-

termine the possible values of

∗

− ¯x

and the corresponding probabilities.

For small n this can be done (see Exercise 18.5), but for large n this becomes

cumbersome. Therefore we invoke a second approximation.

Recall the jury example in Section 6.3, where we investigated the variation

of two diﬀerent rules that a jury might use to assign grades. In terms of

the present chapter, the jury example deals with a random sample from a

U(−0.5, 0.5) distribution and two diﬀerent sample statistics T and M,cor-

responding to the two rules. To investigate the distribution of T and M,

a simulation was carried out with one thousand runs, where in every run we

generated a realization of a random sample from the U(−0.5, 0.5) distribution

and computed the corresponding realization of T and M. The one thousand

realizations give a good impression of how T and M vary around the deserved

score (see Figure 6.4).

Returning to the distribution of

∗

−¯x

, the analogue would be to repeatedly

generate a realization of the bootstrap random sample from F

and every time

compute the corresponding realization of

∗

− ¯x

. The resulting realizations

would give a good impression about the distribution of

∗

−¯x

. A realization

of the bootstrap random sample is called a bootstrap dataset and is denoted

∗

,...,x

∗

to distinguish it from the original dataset x

,...,x

. For the centered

sample mean the simulation procedure is as follows.

274 18 The bootstrap

Empirical bootstrap simulation (for

−µ). Given a dataset

,...,x

, determine its empirical distribution function F

as an

estimate of F , and compute the expectation

∗

=¯x

+ x

+ ···+ x

corresponding to F

1. Generate a bootstrap dataset x

∗

,...,x

∗

from F

2. Compute the centered sample mean for the bootstrap dataset:

¯x

∗

− ¯x

where

¯x

∗

+ x

∗

+ ···+ x

∗

Repeat steps 1 and 2 many times.

Note that generating a value x

∗

from F

is equivalent to choosing one of the

elements x

,...,x

of the original dataset with equal probability 1/n.

The empirical bootstrap simulation is described for the centered sample mean,

but clearly a similar simulation procedure can be formulated for any (normal-

ized) sample statistic.

Remark 18.3 (Some history). Although Efron [7] in 1979 drew attention

to diverse applications of the empirical bootstrap simulation, it already

existed before that time, but not as a uniﬁed widely applicable technique.

See Hall [14] for references to earlier ideas along similar lines and to further

development of the bootstrap. One of Efron’s contributions was to point out

how to combine the bootstrap with modern computational power. In this

way, the interest in this procedure is a typical consequence of the inﬂuence of

computers on the development of statistics in the past decades. Efron also

coined the term “bootstrap,” which is inspired by the American version

of one of the tall stories of the Baron von M¨unchhausen, who claimed to

have lifted himself out of a swamp by pulling the strap on his boot (in the

European version he lifted himself by pulling his hair).

Quick exercise 18.2 Describe the empirical bootstrap simulation for the

centered sample median Med(X

,...,X

) − F

inv

(0.5).

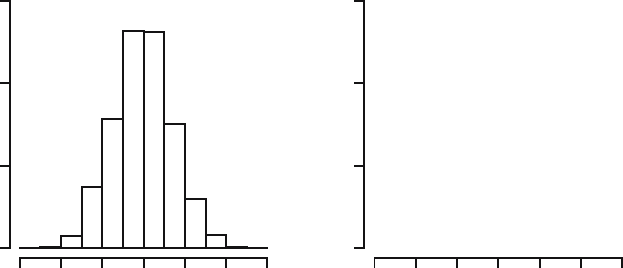
For the Old Faithful data we carried out the empirical bootstrap simulation

for the centered sample mean with one thousand repetitions. In Figure 18.1

a histogram (left) and kernel density estimate (right) are displayed of one

thousand centered bootstrap sample means

¯x

∗

n,1

− ¯x

¯x

∗

n,2

− ¯x

··· ¯x

∗

n,1000

− ¯x

18.2 The empirical bootstrap 275

-18 -12 -6 0 6 12 18

0.02

0.04

0.06

-18 -12 -6 0 6 12 18

0.02

0.04

0.06

.....................

..........

....

...

....

......

............

.............

Fig. 18.1. Histogram and kernel density estimate of centered bootstrap sample

means.

Since these are realizations of the random variable

∗

− ¯x

,weknowfrom

Section 17.2 that they reﬂect the distribution of

∗

− ¯x

. Hence, as the dis-

tribution of

∗

− ¯x

approximates that of

− µ, the centered bootstrap

sample means also reﬂect the distribution of

−µ. This leads to the following

application.

An application of the empirical bootstrap

Let us return to our example about the Old Faithful data, which are mod-

eled as a realization of a random sample from some F . Suppose we estimate

the expectation µ corresponding to F by ¯x

= 209.3. Can we say how far

away 209.3 is from the “true” expectation µ? To be honest, the answer is

no...(oops). In a situation like this, the measurements and their correspond-

ing average are subject to randomness, so that we cannot say anything with

absolute certainty about how far away the average will be from µ.Oneofthe

things we can say is how likely it is that the average is within a given distance

from µ.

To get an impression of how close the average of a dataset of n = 272 ob-

served durations of the Old Faithful geyser is to µ, we want to compute the

probability that the sample mean deviates more than 5 from µ:



− µ| > 5



Direct computation of this probability is impossible, because we do not know

the distribution of the random variable

−µ. However, since the distribution

∗

− ¯x

approximates the distribution of

−µ, we can approximate the

probability as follows



− µ| > 5



≈ P



∗

− ¯x

| > 5





∗

− 209.3| > 5



276 18 The bootstrap

where we have also used that for the Old Faithful data, ¯x

= 209.3. As we

mentioned before, in principle it is possible to compute the last probability

exactly. Since this is too cumbersome, we approximate P



∗

− 209.3| > 5



by means of the one thousand centered bootstrap sample means obtained from

the empirical bootstrap simulation:

¯x

∗

n,1

− 209.3¯x

∗

n,2

− 209.3 ··· ¯x

∗

n,1000

− 209.3.

In view of Table 17.2, a natural estimate for P



∗

− 209.3| > 5



is the relative

frequency of centered bootstrap sample means that are greater than 5 in

absolute value:

number of i with |¯x

∗

n,i

− 209.3| greater than 5

1000

For the centered bootstrap sample means of Figure 18.1, this relative fre-

quency is 0.227. Hence, we obtain the following bootstrap approximation



− µ| > 5



≈ P



∗

− 209.3| > 5



≈ 0.227.

It should be emphasized that the second approximation can be made ar-

bitrarily accurate by increasing the number of repetitions in the bootstrap

procedure.

18.3 The parametric bootstrap

Suppose we consider our dataset as a realization of a random sample from a

distribution of a speciﬁc parametric type. In that case the distribution function

is completely determined by a parameter or vector of parameters θ: F = F

Then we do not have to estimate the whole distribution function F , but it

suﬃces to estimate the parameter(vector) θ by

θ and estimate F by

F = F

The corresponding bootstrap principle is called the parametric bootstrap.

Let us investigate what this would mean for the centered sample mean. First

we should realize that the expectation of F

is also determined by θ: µ = µ

The parametric bootstrap for the centered sample mean now amounts to the

following. The random sample X

,...,X

from the “true” distribution

function F

is replaced by a bootstrap random sample X

∗

,...,X

∗

from

, and the probability distribution of

− µ

is approximated by that of

∗

− µ

∗

,where

∗

= µ

denotes the expectation corresponding to F

Often the parametric bootstrap approximation is better than the empirical

bootstrap approximation, as illustrated in the next quick exercise.

18.3 The parametric bootstrap 277

Quick exercise 18.3 Suppose the dataset x

,...,x

is a realization of a

random sample X

,...,X

from an N (µ, 1) distribution. Estimate µ by

¯x

and consider a bootstrap random sample X

∗

,...,X

∗

from an N (¯x

, 1)

distribution. Check that the probability distributions of

−µ and

∗

− ¯x

are the same:anN(0, 1/n) distribution.

Once more, in principle it is possible to determine the distribution of

∗

−µ

exactly. However, in contrast with the situation considered in the previous

quick exercise, in some cases this is still cumbersome. Again a simulation

procedure may help us out. For the centered sample mean the procedure is as

follows.

Parametric bootstrap simulation (for

− µ). Given a

dataset x

,...,x

, compute an estimate

θ for θ. Determine F

as an estimate for F

, and compute the expectation µ

∗

= µ

corre-

sponding to F

1. Generate a bootstrap dataset x

∗

,...,x

∗

from F

2. Compute the centered sample mean for the bootstrap dataset:

¯x

∗

− µ

where

¯x

∗

+ x

∗

+ ···+ x

∗

Repeat steps 1 and 2 many times.

As an application we will use the parametric bootstrap simulation to investi-

gate whether the exponential distribution is a reasonable model for the soft-

ware data.

Are the software data exponential?

Consider ﬁtting an exponential distribution to the software data, as discussed

in Section 17.3. At ﬁrst sight, Figure 17.6 shows a reasonable ﬁt with the ex-

ponential distribution. One way to quantify the diﬀerence between the dataset

and the exponential model is to compute the maximum distance between the

empirical distribution function F

of the dataset and the exponential distri-

bution function F

estimated from the dataset:

=sup

a∈R

(a) − F

(a)|.

Here F

(a)=0fora<0and

(a)=1− e

−

λa

for a ≥ 0,

where

λ =1/¯x

is estimated from the dataset. The quantity t

is called the

Kolmogorov-Smirnov distance between F

and F

278 18 The bootstrap

The idea behind the use of this distance is the following. If F denotes the

“true” distribution function, then according to Section 17.2 the empirical

distribution function F

will resemble F whether F equals the distribution

function F

of some Exp(λ) distribution or not. On the other hand, if the

“true” distribution function is F

, then the estimated exponential distribu-

tion function F

will resemble F

, because

λ =1/¯x

is close to the “true” λ.

Therefore, if F = F

,thenbothF

and F

will be close to the same distribu-

tion function, so that t

is small; if F is diﬀerent from F

,thenF

and F

are close to two diﬀerent distribution functions, so that t

is large. The value

is always between 0 and 1, and the further away this value is from 0, the

more it is an indication that the exponential model is inappropriate. For the

software dataset we ﬁnd

λ =1/¯x

=0.0015 and t

=0.176. Does this speak

against the believed exponential model?

One way to investigate this is to ﬁnd out whether, in the case when the data are

truly a realization of an exponential random sample from F

, the value 0.176 is

unusually large. To answer this question we consider the sample statistic that

corresponds to t

. The estimate

λ =1/¯x

is replaced by the random variable

Λ =1/

, and the empirical distribution function of the dataset is replaced

by the empirical distribution function of the random sample X

,...,X

(again denoted by F

(a)=

number of X

less than or equal to a

In this way, t

is a realization of the sample statistic

=sup

a∈R

(a) − F

(a)|.

To ﬁnd out whether 0.176 is an exceptionally large value for the random vari-

able T

, we must determine the probability distribution of T

. However, this

is impossible because the parameter λ of the Exp(λ) distribution is unknown.

We will approximate the distribution of T

by a parametric bootstrap. We use

the dataset to estimate λ by

λ =1/¯x

=0.0015 and replace the random sam-

ple X

,...,X

from F

by a bootstrap random sample X

∗

,...,X

∗

from F

. Next we approximate the distribution of T

by that of its boot-

strapped version

∗

=sup

a∈R

∗

(a) − F

∗

(a)|,

where F

∗

is the empirical distribution function of the bootstrap random sam-

ple:

∗

(a)=

number of X

∗

less than or equal to a

and

∗

=1/

∗

,with

∗

being the average of the bootstrap random sample.

The bootstrapped sample statistic T

∗

is too complicated to determine its

probability distribution, and hence we perform a parametric bootstrap simu-

lation:

18.4 Solutions to the quick exercises 279

1. We generate a bootstrap dataset x

∗

,...,x

∗

135

from an exponential dis-

tribution with parameter

λ =0.0015.

2. We compute the bootstrapped KS distance

∗

=sup

a∈R

∗

(a) − F

∗

(a)|,

where F

∗

denotes the empirical distribution function of the bootstrap

dataset and F

∗

denotes the estimated exponential distribution function,

where

∗

=1/¯x

∗

is computed from the bootstrap dataset.

We repeat steps 1 and 2 one thousand times, which results in one thousand

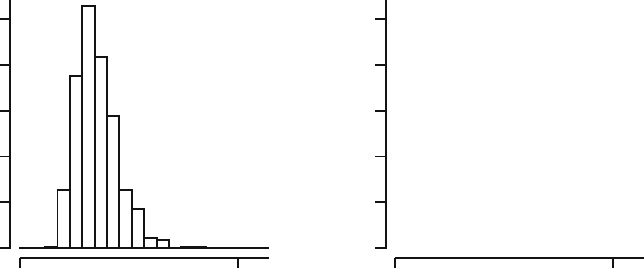
values of the bootstrapped KS distance. In Figure 18.2 we have displayed a

histogram and kernel density estimate of the one thousand bootstrapped KS

distances. It is clear that if the software data would come from an exponential

distribution, the value 0.176 of the KS distance would be very unlikely! This

strongly suggests that the exponential distribution is not the right model for

the software data. The reason for this is that the Poisson process is the wrong

model for the series of failures. A closer inspection shows that the rate at

which failures occur over time is not constant, as was assumed in Chapter 17,

but decreases.

0 0.176

............................

...........

....

...

.....

........................

....

.........................................................................

Fig. 18.2. One thousand bootstrapped KS distances.

18.4 Solutions to the quick exercises

18.1 You could have written something like the following: “Use the dataset

,...,x

to compute an estimate

F for F . Replace the random sample

,...,X

from F by a random sample X

∗

,...,X

∗

from

F ,and

approximate the probability distribution of

280 18 The bootstrap

Med(X

,...,X

) − F

inv

(0.5)

by that of Med(X

∗

,...,X

∗

) −

inv

(0.5),where

inv

(0.5) is the median

F .”

18.2 You could have written something like the following: “Given a dataset

,...,x

, determine its empirical distribution function F

as an estimate

of F ,andthemedianF

inv

(0.5) of F

1. Generate a bootstrap dataset x

∗

,...,x

∗

from F

2. Compute the sample median for the bootstrap dataset:

Med

∗

− F

inv

(0.5),

where Med

∗

= sample median of x

∗

,...,x

∗

Repeat steps 1 and 2 many times.”

Note that if n is odd, then F

inv

(0.5) equals the sample median of the original

dataset, but this is not necessarily so for n even.

18.3 According to Remark 11.2 about the sum of independent normal ran-

dom variables, the sum of n independent N(µ, 1) distributed random variables

has an N (nµ, n) distribution. Hence by the change-of-units rule for the normal

distribution (see page 106), it follows that

has an N(µ, 1/n) distribution,

and that

− µ has an N(0, 1/n) distribution. Similarly, the average

∗

n independent N (¯x

, 1) distributed bootstrap random variables has a nor-

mal distribution N (¯x

, 1/n) distribution, and therefore

∗

− ¯x

again has an

N(0, 1/n) distribution.

18.5 Exercises

18.1  We generate a bootstrap dataset x

∗

,...,x

∗

from the empirical

distribution function of the dataset

211463,

i.e., we draw (with replacement) six values from these numbers with equal

probability 1/6. How many diﬀerent bootstrap datasets are possible? Are

they all equally likely to occur?

18.2 We generate a bootstrap dataset x

∗

from the empirical distri-

bution function of the dataset

1346.

a. Compute the probability that the bootstrap sample mean is equal to 1.

18.5 Exercises 281

b. Compute the probability that the maximum of the bootstrap dataset is

equal to 6.

c. Compute the probability that exactly two elements in the bootstrap sam-

ple are less than 2.

18.3  We generate a bootstrap dataset x

∗

,...,x

∗

from the empirical

distribution function of the dataset

0.39 0.41 0.38 0.44 0.40

0.36 0.34 0.46 0.35 0.37.

a. Compute the probability that the bootstrap dataset has exactly three

elements equal to 0.35.

b. Compute the probability that the bootstrap dataset has at most two ele-

ments less than or equal to 0.38.

c. Compute the probability that the bootstrap dataset has exactly two ele-

ments less than or equal to 0.38 and all other elements greater than 0.42.

18.4  Consider the dataset from Exercise 18.3, with maximum 0.46.

a. We generate a bootstrap random sample X

∗

,...,X

∗

from the empir-

ical distribution function of the dataset. Compute P(M

∗

< 0.46), where

∗

=max{X

∗

,...,X

∗

b. The same question as in a, but now for a dataset with distinct elements

,...,x

and maximum m

. Compute P(M

∗

), where M

∗

the maximum of a bootstrap random sample X

∗

,...,X

∗

generated

from the empirical distribution function of the dataset.

18.5  Suppose we have a dataset

036,

which is the realization of a random sample from a distribution function F .If

we estimate F by the empirical distribution function, then according to the

bootstrap principle applied to the centered sample mean

− µ,wemust

replace this random variable by its bootstrapped version

∗

− ¯x

. Determine

the possible values for the bootstrap random variable

∗

− ¯x

and the corre-

sponding probabilities.

18.6 Suppose that the dataset x

,...,x

is a realization of a random

sample from an Exp (λ) distribution with distribution function F

,andthat

¯x

=5.

a. Check that the median of the Exp (λ) distribution is m

=(ln2)/λ (see

also Exercise 5.11).

b. Suppose we estimate λ by 1/¯x

. Describe the parametric bootstrap sim-

ulation for Med(X

,...,X

) − m

282 18 The bootstrap

18.7  To give an example in which the bootstrapped centered sample mean

in the parametric and empirical bootstrap simulations may be diﬀerent,con-

sider the following situation. Suppose that the dataset x

,...,x

is a re-

alization of a random sample from a U (0,θ) distribution with expectation

µ = θ/2. We estimate θ by

θ =

n +1

where m

=max{x

,...,x

}. Describe the parametric bootstrap simula-

tion for the centered sample mean

− µ.

18.8  Here is an example in which the bootstrapped centered sample mean in

the parametric and empirical bootstrap simulations are the same. Consider the

software data with average ¯x

= 656.8815 and median m

= 290, modeled as

a realization of a random sample X

,...,X

from a distribution function

F with expectation µ. By means of bootstrap simulation we like to get an

impression of the distribution of

− µ.

a. Suppose that we assume nothing about the distribution of the interfailure

times. Describe the appropriate bootstrap simulation procedure with one

thousand repetitions.

b. Suppose we assume that F is the distribution function of an Exp(λ) distri-

bution, where λ is estimated by 1/¯x

=0.0015. Describe the appropriate

bootstrap simulation procedure with one thousand repetitions.

c. Suppose we assume that F is the distribution function of an Exp(λ)dis-

tribution, and that (as suggested by Exercise 18.6 a) the parameter λ

is estimated by (ln 2)/m

=0.0024. Describe the appropriate bootstrap

simulation procedure with one thousand repetitions.

18.9  Consider the dataset from Exercises 15.1 and 17.6 consisting of mea-

sured chest circumferences of Scottish soldiers with average ¯x

=39.85 and

sample standard deviation s

=2.09. The histogram in Figure 17.11 suggests

modeling the data as the realization of a random sample X

,...,X

from

an N(µ, σ

) distribution. We estimate µ by the sample mean and we are inter-

ested in the probability that the sample mean deviates more than 1 from µ:



− µ| > 1



. Describe how one can use the bootstrap principle to approx-

imate this probability, i.e., describe the distribution of the bootstrap random

sample X

∗

,...,X

∗

and compute P



∗

− µ

∗

| > 1



. Note that one does

not need a simulation to approximate this latter probability.

18.10 Consider the software data, with average ¯x

= 656.8815, modeled as

a realization of a random sample X

,...,X

from a distribution func-

tion F . We estimate the expectation µ of F by the sample mean and we are

interested in the probability that the sample mean deviates more than ten

from µ:P



− µ| > 10



A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику - Как? и Почему? )

Подождите немного. Документ загружается.