A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику - Как? и Почему? )
Подождите немного. Документ загружается.

19.4 Unbiased estimators for expectation and variance 293
Then from the rules concerning variances of sums of independent random
variables we find that
Var
X
i
−
¯
X
n
=Var
⎛
⎝
n − 1
n
X
i
−
1
n
j=i
X
j
⎞
⎠
=
(n − 1)
2
n
2
Var(X
i
)+
1
n
2
j=i
Var(X
j
)
=
(n − 1)
2
n
2
+
n − 1
n
2
σ
2
=
n − 1
n
σ
2
.
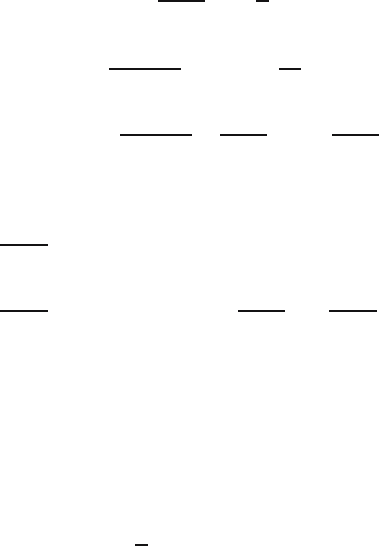
We conclude that
E
S
2
n
=
1
n − 1
n
i=1
E
(X
i
−
¯
X
n
)
2
=
1
n − 1
n
i=1
Var
X
i
−
¯
X
n
=
1
n − 1
·n ·
n − 1
n
σ
2
= σ
2
.
This explains why we divide by n −1 in the formula for S
2
n
; only in this case
S
2
n
is an unbiased estimator for the “true” variance σ
2
. If we would divide by
n instead of n −1, we would obtain an estimator with negative bias; it would
systematically produce too-small estimates for σ
2
.
Quick exercise 19.3 Consider the following estimator for σ
2
:
V
2
n
=
1
n
n
i=1
(X
i
−
¯
X
n
)
2
.
Compute the bias E
V
2
n
−σ
2
for this estimator, where you can keep compu-
tations simple by realizing that V
2
n
=(n − 1)S
2
n
/n.
Unbiasedness does not always carry over
We have seen that S
2
n
is an unbiased estimator for the “true” variance σ
2
.A
natural question is whether S
n
is again an unbiased estimator for σ.Thisisnot
the case. Since the function g(x)=x
2
is strictly convex, Jensen’s inequality
yields that
σ
2
=E
S
2
n
> (E [S
n
])
2
,
which implies that E[S
n
] <σ. Another example is the network arrivals, in
which
¯
X
n
is an unbiased estimator for µ,wherease
−
¯
X
n
is positively biased
with respect to e
−µ
. These examples illustrate a general fact: unbiasedness
does not always carry over, i.e., if T is an unbiased estimator for a parameter θ,
then g(T ) does not have to be an unbiased estimator for g(θ).

294 19 Unbiased estimators
However, there is one special case in which unbiasedness does carry over,
namely if g(T )=aT + b.Indeed,ifT is unbiased for θ:E[T ]=θ, then by the
change-of-units rule for expectations,
E[aT + b]=aE[T ]+b = aθ + b,
which means that aT + b is unbiased for aθ + b.
19.5 Solutions to the quick exercises
19.1 Write y for the number of x
i
equal to zero. Denote the probability of
zero by p
0
,sothatp
0
=e
−µ
. This means that µ = −ln(p
0
). Hence if we
estimate p
0
by the relative frequency y/n, we can estimate µ by −ln(y/n).
19.2 The function g(x)=−ln(x) is strictly convex, since g
(x)=1/x
2
> 0.
Hence by Jensen’s inequality
E[U]=E[−ln(S)] > −ln(E [S]).
Since we have seen that E[S]=p
0
=e
−µ
, it follows that E [U ] > −ln(E[S]) =
−ln(e
−µ
)=µ. This means that U has positive bias.
19.3 Using that E
S
2
n
= σ
2
, we find that
E
V
2
n
=E
n − 1
n
S
2
n
=
n − 1
n
E
S
2
n
=
n − 1
n
σ
2
.
We conclude that the bias of V
2
n
equals E
V
2
n
− σ
2
= −σ
2
/n < 0.
19.6 Exercises
19.1 Suppose our dataset is a realization of a random sample X
1
,X
2
,...,X
n
from a uniform distribution on the interval [−θ, θ], where θ is unknown.
a. Show that
T =
3
n
(X
2
1
+ X
2
2
+ ···+ X
2
n
)
is an unbiased estimator for θ
2
.
b. Is
√
T also an unbiased estimator for θ? If not, argue whether it has
positive or negative bias.
19.2 Suppose the random variables X
1
,X
2
,...,X
n
have the same expecta-
tion µ.

19.6 Exercises 295
a. Is S =
1
2
X
1
+
1
3
X
2
+
1
6
X
3
an unbiased estimator for µ?
b. Under what conditions on constants a
1
,a
2
,...,a
n
is
T = a
1
X
1
+ a
2
X
2
+ ···+ a
n
X
n
an unbiased estimator for µ?
19.3 Suppose the random variables X
1
,X
2
,...,X
n
have the same expec-
tation µ. For which constants a and b is
T = a(X
1
+ X
2
+ ···+ X
n
)+b
an unbiased estimator for µ?
19.4 Recall Exercise 17.5 about the number of cycles to pregnancy. Suppose
the dataset corresponding to the table in Exercise 17.5 a is modeled as a
realization of a random sample X
1
,X
2
,...,X
n
from a Geo(p) distribution,
where 0 <p<1 is unknown. Motivated by the law of large numbers, a
natural estimator for p is
T =1/
¯
X
n
.
a. Check that T is a biased estimator for p and find out whether it has
positive or negative bias.
b. In Exercise 17.5 we discussed the estimation of the probability that a
woman becomes pregnant within three or fewer cycles. One possible esti-
mator for this probability is the relative frequency of women that became
pregnant within three cycles
S =
number of X
i
≤ 3
n
.
Show that S is an unbiased estimator for this probability.
19.5 Suppose a dataset is modeled as a realization of a random sample
X
1
,X
2
,...,X
n
from an Exp(λ) distribution, where λ>0 is unknown. Let
µ denote the corresponding expectation and let M
n
denote the minimum of
X
1
,X
2
,...,X
n
. Recall from Exercise 8.18 that M
n
has an Exp(nλ) distribu-
tion. Find out for which constant c the estimator
T = cM
n
is an unbiased estimator for µ.
19.6 Consider the following dataset of lifetimes of ball bearings in hours.
6278 3113 5236 11584 12628 7725 8604 14266 6125 9350
3212 9003 3523 12888 9460 13431 17809 2812 11825 2398
Source: J.E. Angus. Goodness-of-fit tests for exponentiality based on a loss-
of-memory type functional equation. Journal of Statistical Planning and In-
ference, 6:241-251, 1982; example 5 on page 249.
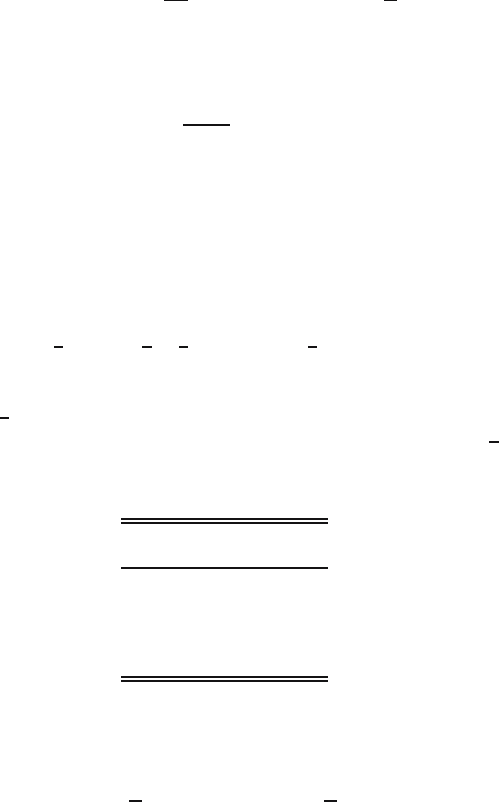
296 19 Unbiased estimators
One is interested in estimating the minimum lifetime of this type of ball bear-
ing. The dataset is modeled as a realization of a random sample X
1
,...,X
n
.
Each random variable X
i
is represented as
X
i
= δ + Y
i
,
where Y
i
has an Exp(λ) distribution and δ>0 is an unknown parameter that
is supposed to model the minimum lifetime. The objective is to construct an
unbiased estimator for δ.Itisknownthat
E[M
n
]=δ +
1
nλ
and E
¯
X
n
= δ +
1
λ
,
where M
n
= minimum of X
1
,X
2
,...,X
n
and
¯
X
n
=(X
1
+ X
2
+ ···+ X
n
)/n.
a. Check that
T =
n
n − 1
¯
X
n
− M
n
is an unbiased estimator for 1/λ.
b. Construct an unbiased estimator for δ.
c. Use the dataset to compute an estimate for the minimum lifetime δ.You
may use that the average lifetime of the data is 8563.5.
19.7 Leaves are divided into four different types: starchy-green, sugary-white,
starchy-white, and sugary-green. According to genetic theory, the types occur
with probabilities
1
4
(θ +2),
1
4
θ,
1
4
(1 − θ), and
1
4
(1 − θ), respectively, where
0 <θ<1. Suppose one has n leaves. Then the number of starchy-green
leaves is modeled by a random variable N
1
with a Bin (n, p
1
) distribution,
where p
1
=
1
4
(θ + 2), and the number of sugary-white leaves is modeled by
a random variable N
2
with a Bin (n, p
2
) distribution, where p
2
=
1
4
θ.The
following table lists the counts for the progeny of self-fertilized heterozygotes
among 3839 leaves.
Type Count
Starchy-green 1997
Sugary-white 32
Starchy-white 906
Sugary-green 904
Source: R.A. Fisher. Statistical methods for research workers.Hafner,New
York, 1958; Table 62 on page 299.
Consider the following two estimators for θ:
T
1
=
4
n
N
1
− 2andT
2
=
4
n
N
2
.

19.6 Exercises 297
a. Check that both T
1
and T
2
are unbiased estimators for θ.
b. Compute the value of both estimators for θ.
19.8 Recall the black cherry trees example from Exercise 17.9, modeled by
a linear regression model without intercept
Y
i
= βx
i
+ U
i
for i =1, 2,...,n,
where U
1
,U
2
,...,U
n
are independent random variables with E[U
i
]=0and
Var(U
i
)=σ
2
. We discussed three estimators for the parameter β:
B
1
=
1
n
Y
1
x
1
+ ···+
Y
n
x
n
,
B
2
=
Y
1
+ ···+ Y
n
x
1
+ ···+ x
n
,
B
3
=
x
1
Y
1
+ ···+ x
n
Y
n
x
2
1
+ ···+ x
2
n
.
Show that all three estimators are unbiased for β.
19.9 Consider the network example where the dataset is modeled as a real-
ization of a random sample X
1
,X
2
,...,X
n
from a Pois (µ) distribution. We
estimate the probability of zero arrivals e
−µ
by means of T =e
−
¯
X
n
.Check
that
E[T ]=e
−nµ(1−e
−1/n
)
.
Hint: write T =e
−Z/n
,whereZ = X
1
+ X
2
+ ···+ X
n
has a Pois (nµ)
distribution.

20
Efficiency and mean squared error
In the previous chapter we introduced the notion of unbiasedness as a de-
sirable property of an estimator. If several unbiased estimators for the same
parameter of interest exist, we need a criterion for comparison of these estima-
tors. A natural criterion is some measure of spread of the estimators around
the parameter of interest. For unbiased estimators we will use variance. For
arbitrary estimators we introduce the notion of mean squared error (MSE),
which combines variance and bias.
20.1 Estimating the number of German tanks
In this section we come back to the problem of estimating German war produc-
tion as discussed in Section 1.5. We consider serial numbers on tanks, recoded
to numbers running from 1 to some unknown largest number N . Given is a
subset of n numbers of this set. The objective is to estimate the total number
of tanks N on the basis of the observed serial numbers.
Denote the observed distinct serial numbers by x
1
,x
2
,...,x
n
. This dataset
can be modeled as a realization of random variables X
1
,X
2
,...,X
n
repre-
senting n draws without replacement from the numbers 1, 2,...,N with equal
probability. Note that in this example our dataset is not a realization of a
random sample, because the random variables X
1
,X
2
,...,X
n
are dependent.
We propose two unbiased estimators. The first one is based on the sample
mean
¯
X
n
=
X
1
+ X
2
+ ···+ X
n
n
,
and the second one is based on the sample maximum
M
n
=max{X
1
,X
2
,...,X
n
}.
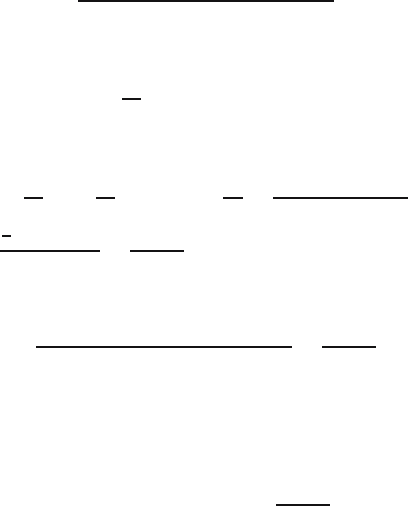
300 20 Efficiency and mean squared error
An estimator based on the sample mean
To construct an unbiased estimator for N basedonthesamplemean,westart
by computing the expectation of
¯
X
n
. The linearity-of-expectations rule also
applies to dependent random variables, so that
E
¯
X
n
=
E[X
1
]+E[X
2
]+···+E[X
n
]
n
.
In Section 9.3 we saw that the marginal distribution of each X
i
is the same:
P(X
i
= k)=
1
N
for k =1, 2,...,N.
Therefore the expectation of each X
i
is given by
E[X
i
]=1·
1
N
+2·
1
N
+ ···+ N ·
1
N
=
1+2+···+ N
N
=
1
2
N(N +1)
N
=
N +1
2
.
It follows that
E
¯
X
n
=
E[X
1
]+E[X
2
]+···+E[X
n
]
n
=
N +1
2
.
This directly implies that
T
1
=2
¯
X
n
− 1
is an unbiased estimator for N, since the change-of-units rule yields that
E[T
1
]=E
2
¯
X
n
− 1
=2E
¯
X
n
− 1=2·
N +1
2
− 1=N.
Quick exercise 20.1 Suppose we have observed tanks with (recoded) serial
numbers
61 19 56 24 16.
Compute the value of the estimator T
1
for the total number of tanks.
An estimator based on the sample maximum
To construct an unbiased estimator for N based on the maximum, we first
compute the expectation of M
n
. We start by computing the probability that
M
n
= k,wherek takes the values n,...,N. Similar to the combinatorics
used in Section 4.3 to derive the binomial distribution, the number of ways
to draw n numbers without replacement from 1, 2,...,N is
N
n
. Hence each
combination has probability 1/
N
n
.InordertohaveM
n
= k,wemusthave
one number equal to k and choose the other n−1 numbers out of the numbers
1, 2,...,k−1. There are
k−1
n−1
ways to do this. Hence for the possible values
k = n, n +1,...,N,
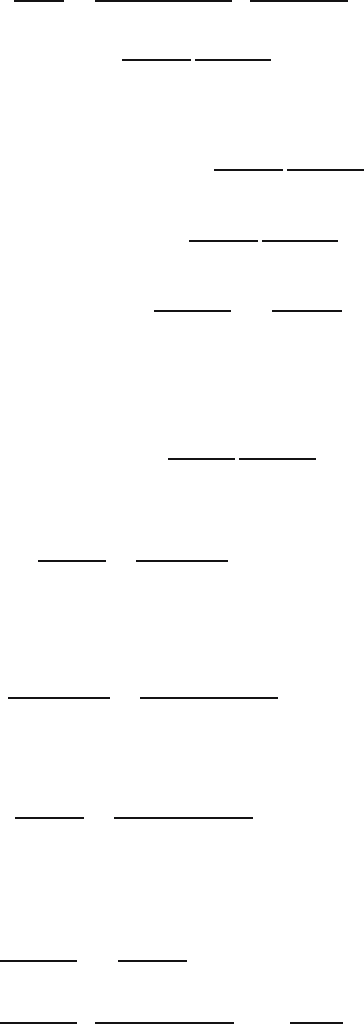
20.1 Estimating the number of German tanks 301
P(M
n
= k)=
k−1
n−1
N
n
=
(k − 1)!
(k − n)!(n − 1)!
·
(N −n)! n!
N!
= n ·
(k − 1)!
(k − n)!
(N − n)!
N!
.
Thus the expectation of M
n
is given by
E[M
n
]=
N
k=n
kP(M
n
= k)=
N
k=n
k · n ·
(k − 1)!
(k − n)!
(N − n)!
N!
=
N
k=n
n ·
k!
(k − n)!
(N − n)!
N!
= n ·
(N − n)!
N!
N
k=n
k!
(k − n)!
.
How to continue the computation of E [M
n
]? We use a trick: we start by
rearranging
1=
N
j=n
P(M
n
= j)=
N
j=n
n ·
(j − 1)!
(j − n)!
(N − n)!
N!
,
finding that
N
j=n
(j − 1)!
(j − n)!
=
N!
n (N − n)!
. (20.1)
This holds for any N and any n ≤ N. In particular we could replace N by
N +1andn by n +1:
N+1
j=n+1
(j − 1)!
(j − n − 1)!
=
(N +1)!
(n +1)(N − n)!
.
Changing the summation variable to k = j − 1, we obtain
N
k=n
k!
(k − n)!
=
(N +1)!
(n +1)(N − n)!
. (20.2)
This is exactly what we need to finish the computation of E [M
n
]. Substituting
(20.2) in what we obtained earlier, we find
E[M
n
]=n ·
(N − n)!
N!
N
k=n
k!
(k − n)!
= n ·
(N − n)!
N!
·
(N +1)!
(n +1)(N − n)!
= n ·
N +1
n +1
.
302 20 Efficiency and mean squared error
Quick exercise 20.2 Choosing n = N in this formula yields E [M
N
]=N.
Can you argue that this is the right answer without doing any computations?
With the formula for E [M
n
] we can derive immediately that
T
2
=
n +1
n
M
n
− 1
is an unbiased estimator for N, since by the change-of-units rule,
E[T
2
]=E
n +1
n
M
n
− 1
=
n +1
n
E[M
n
] − 1=
n +1
n
·
n(N +1)
n +1
− 1=N.
Quick exercise 20.3 Compute the value of estimator T
2
for the total number
of tanks on basis of the observed numbers from Quick exercise 20.1.
20.2 Variance of an estimator
In the previous section we saw that we can construct two completely different
estimators for the total number of tanks N that are both unbiased. The obvious
question is: which of the two is better? To answer this question, we investigate
how both estimators vary around the parameter of interest N. Although we
could in principle compute the distributions of T
1
and T
2
, we carry out a
small simulation study instead. Take N = 1000 and n = 10 fixed. We draw
10 numbers, without replacement, from 1, 2,...,1000 and compute the value
of the estimators T
1
and T
2
. We repeat this two thousand times, so that we
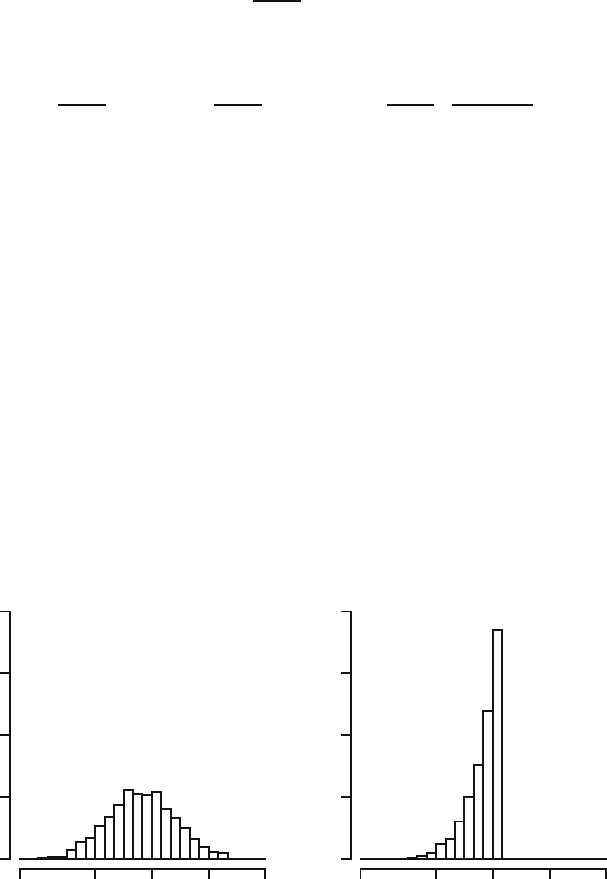
have 2000 values for both estimators. In Figure 20.1 we have displayed the
histogram of the 2000 values for T
1
on the left and the histogram of the 2000
values for T
2
on the right. From the histograms, which reflect the probability
300 700 N = 1000 1300 1600
0
0.002
0.004
0.006
0.008
300 700 N = 1000 1300 1600
0
0.002
0.004
0.006
0.008
Fig. 20.1. Histograms of two thousand values for T
1
(left) and T
2
(right).

20.2 Variance of an estimator 303
mass functions of both estimators, we see that the distributions of T
1
and
T
2
are of completely different types. As can be expected from the fact that
both estimators are unbiased, the values vary around the parameter of interest
N = 1000. The most important difference between the histograms is that the
variation in the values of T
2
is less than the variation in the values of T
1
.
This suggests that estimator T
2
estimates the total number of tanks more
efficiently than estimator T
1
, in the sense that it produces estimates that
are more concentrated around the parameter of interest N than estimates
produced by T
1
. Recall that the variance measures the spread of a random
variable. Hence the previous discussion motivates the use of the variance of
an estimator to evaluate its performance.
Efficiency. Let T
1
and T
2
be two unbiased estimators for the same
parameter θ. Then estimator T
2
is called more efficient than estima-
tor T
1
if Var(T
2
) < Var(T
1
), irrespective of the value of θ.
Let us compare T
1
and T
2
using this criterion. For T
1
we have
Var(T
1
)=Var
2
¯
X
n
− 1
=4Var
¯
X
n
.
Although the X
i
are not independent, it is true that all pairs (X
i
,X
j
)with
i = j have the same distribution (this follows in the same way in which
we showed on page 122 that all X
i
have the same distribution). With the
variance-of-the-sum rule for n random variables (see Exercise 10.17), we find
that
Var(X
1
+ ···+ X
n
)=nVar(X
1
)+n(n − 1)Cov(X
1
,X
2
) .
In Exercises 9.18 and 10.18, we computed that
Var(X
1
)=
1
12
(N − 1)(N +1), Cov(X
1
,X
2
)=−
1
12
(N +1).
We find therefore that
Var(T
1
) = 4Var
¯
X
n
=
4
n
2
Var(X
1
+ ···+ X
n
)
=
4
n
2
n ·
1
12
(N −1)(N +1)− n(n − 1) ·
1
12
(N +1)
=
1
3n
(N +1)[N − 1 − (n − 1)]
=
(N +1)(N − n)
3n
.
Obtaining the variance of T
2
is a little more work. One can compute the
variance of M
n
in a way that is very similar to the way we obtained E[M
n
].
The result is (see Remark 20.1 for details)
Var(M
n
)=
n(N +1)(N − n)
(n +2)(n +1)
2
.
