A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику

21.6 Exercises 325

b. Now suppose that the density of this normal distribution is given by

f

σ

(x)=

1

σ

√

2π

e

−

1

2

x

2

/σ

2

for −∞ <x<∞.

Determine the maximum likelihood estimate for σ.

21.6 Let x

1

,x

2

,...,x

n

be a dataset that is a realization of a random sample

from a distribution with probability density f

δ

(x)givenby

f

δ

(x)=



e

−(x−δ)

for x ≥ δ

0forx<δ.

a. Draw the likelihood L(δ).

b. Determine the maximum likelihood estimate for δ.

21.7  Suppose that x

1

,x

2

,...,x

n

is a dataset, which is a realization of a ran-

dom sample from a Rayleigh distribution, which is a continuous distribution

with probability density function given by

f

θ

(x)=

x

θ

2

e

−

1

2

x

2

/θ

2

for x ≥ 0.

In this case what is the maximum likelihood estimate for θ?

21.8  (Exercises 19.7 and 20.7 continued) A certain type of plant can be di-

vided into four types: starchy-green, starchy-white, sugary-green, and sugary-

white. The following table lists the counts of the various types among 3839

leaves.

Type Count

Starchy-green 1997

Sugary-white 32

Starchy-white 906

Sugary-green 904

Setting

X =

⎧

⎪

⎨

⎪

⎩

1 if the observed leave is of type starchy-green

2 if the observed leave is of type sugary-white

3 iftheobservedleaveisoftypestarchy-white

4 if the observed leave is of type sugary-green,

the probability mass function p of X is given by

a 123 4

p(a)

1

4

(2 + θ)

1

4

θ

1

4

(1 − θ)

1

4

(1 − θ)

326 21 Maximum likelihood

and p(a) = 0 for all other a.Here0<θ<1 is an unknown parameter,

which was estimated in Exercise 19.7. We want to ﬁnd a maximum likelihood

estimate of θ.

a. Use the data to ﬁnd the likelihood L(θ) and the loglikelihood (θ).

b. What is the maximum likelihood estimate of θ using the data from the

preceding table?

c. Suppose that we have the counts of n diﬀerent leaves: n

1

of type starchy-

green, n

2

of type sugary-white, n

3

of type starchy-white, and n

4

of type

sugary-green (so n = n

1

+ n

2

+ n

3

+ n

4

). Determine the general formula

for the maximum likelihood estimate of θ.

21.9  Let x

1

,x

2

,...,x

n

be a dataset that is a realization of a random sample

from a U(α, β) distribution (with α and β unknown, α<β). Determine the

maximum likelihood estimates for α and β.

21.10 Let x

1

,x

2

,...,x

n

be a dataset, which is a realization of a random

sample from a Par(α) distribution. What is the maximum likelihood estimate

for α?

21.11  In Exercise 4.13 we considered the situation where we have a box

containing an unknown number—say N—of identical bolts. In order to get an

idea of the size of N we introduced three random variables X, Y ,andZ.Here

we will use X and Y , and in the next exercise Z, to ﬁnd maximum likelihood

estimates of N .

a. Suppose that x

1

,x

2

,...,x

n

is a dataset, which is a realization of a random

sample from a Geo(1/N ) distribution. Determine the maximum likelihood

estimate for N.

b. Suppose that y

1

,y

2

,...,y

n

is a dataset, which is a realization of a random

sample from a discrete uniform distribution on 1, 2,...,N. Determine the

maximum likelihood estimate for N.

21.12 (Exercise 21.11 continued.) Suppose that m bolts in the box were

marked and then r bolts were selected from the box; Z is the number of

marked bolts in the sample. (Recall that it was shown in Exercise 4.13 c that

Z has a hypergeometric distribution, with parameters m, N,andr.) Suppose

that k bolts in the sample were marked. Show that the likelihood L(N )is

given by

L(N)=



m

k



N−m

r−k





N

r

 .

Next show that L(N)increasesforN<mr/kand decreases for N>mr/k,

and conclude that mr/k is the maximum likelihood estimate for N .

21.13 Often one can model the times that customers arrive at a shop rather

well by a Poisson process with (unknown) rate λ (customers/hour). On a

certain day, one of the attendants noticed that between noon and 12.45 p.m.

21.6 Exercises 327

two customers arrived, and another attendant noticed that on the same day

one customer arrived between 12.15 and 1 p.m. Use the observations of the

attendants to determine the maximum likelihood estimate of λ.

21.14 A very inexperienced archer shoots n times an arrow at a disc of (un-

known) radius θ. The disc is hit every time, but at completely random places.

Let r

1

,r

2

,...,r

n

be the distances of the various hits to the center of the disc.

Determine the maximum likelihood estimate for θ.

21.15 On January 28, 1986, the main fuel tank of the space shuttle Challenger

exploded shortly after takeoﬀ. Essential in this accident was the leakage of

some of the six O-rings of the Challenger. In Section 1.4 the probability of

failure of an O-ring is given by

p(t)=

e

a+b·t

1+e

a+b·t

,

where t is the temperature at launch in degrees Fahrenheit. In Table 21.2

the temperature t (in

◦

F, rounded to the nearest integer) and the number of

failures N for 23 missions are given, ordered according to increasing temper-

atures. (See also Figure 1.3, where these data are graphically depicted.) Give

the likelihood L(a, b) and the loglikelihood (a, b).

Table 21.2. Space shuttle failure data of pre-Challenger missions.

t 53 57 58 63 66 67 67 67

N 21110000

t 68 69 70 70 70 70 72 73

N 00001100

t 75 75 76 76 78 79 81

N 0200000

21.16 In the 18th century Georges-Louis Leclerc, Comte de Buﬀon (1707–

1788) found an amusing way to approximate the number π using probability

theory and statistics. Buﬀon had the following idea: take a needle and a large

sheet of paper, and draw horizontal lines that are a needle-length apart. Throw

the needle a number of times (say n times) on the sheet, and count how often it

hits one of the horizontal lines. Say this number is s

n

,thens

n

is the realization

of a Bin(n, p) distributed random variable S

n

.Herep is the probability that

the needle hits one of the horizontal lines. In Exercise 9.20 you found that

p =2/π. Show that

T =

2n

S

n

is the maximum likelihood estimator for π.

22

The method of least squares

The maximum likelihood principle provides a way to estimate parameters. The

applicability of the method is quite general but not universal. For example,

in the simple linear regression model, introduced in Section 17.4, we need to

know the distribution of the response variable in order to ﬁnd the maximum

likelihood estimates for the parameters involved. In this chapter we will see

how these parameters can be estimated using the method of least squares.

Furthermore, the relation between least squares and maximum likelihood will

be investigated in the case of normally distributed errors.

22.1 Least squares estimation and regression

Recall from Section 17.4 the simple linear regression model for a bivariate

dataset (x

1

,y

1

), (x

2

,y

2

),...,(x

n

,y

n

). In this model x

1

,x

2

,...,x

n

are non-

random and y

1

,y

2

,...,y

n

are realizations of random variables Y

1

,Y

2

,...,Y

n

satisfying

Y

i

= α + βx

i

+ U

i

for i =1, 2,...,n,

where U

1

,U

2

,...,U

n

are independent random variables with zero expectation

and variance σ

2

. How can one obtain estimates for the parameters α, β,andσ

2

in this model?

Note that we cannot ﬁnd maximum likelihood estimates for these parameters,

simply because we have no further knowledge about the distribution of the U

i

(and consequently of the Y

i

). We want to choose α and β in such a way that

we obtain a line that ﬁts the data best. A classical approach to do this is to

consider the sum of squared distances between the observed values y

i

and the

values α + βx

i

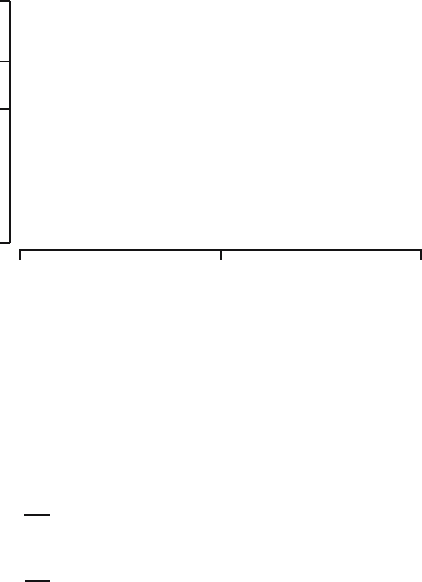
on the regression line y = α + βx. See Figure 22.1, where these

distances are indicated. The method of least squares prescribes to choose α

and β such that the sum of squares

S(α, β)=

n



i=1

(y

i

− α − βx

i

)

2

330 22 The method of least squares

x

i

y

i

α + βx

i



The regression

line y = αx = β

The point (x

i

,y

i

)



.

·

.

..................................

...................................

.

Fig. 22.1. The observed value y

i

corresponding to x

i

and the value α + βx

i

on the

regression line y = α + βx.

is minimal. The ith term in the sum is the squared distance in the vertical

direction from (x

i

,y

i

) to the line y = α + βx. To ﬁnd these so-called least

squares estimates, we diﬀerentiate S(α, β) with respect to α and β,andwe

set the derivatives equal to 0:

∂

∂α

S(α, β)=0 ⇔

n



i=1

(y

i

− α − βx

i

)=0

∂

∂β

S(α, β)=0 ⇔

n



i=1

(y

i

− α − βx

i

) x

i

=0.

This is equivalent to

nα + β

n



i=1

x

i

=

n



i=1

y

i

α

n



i=1

x

i

+ β

n



i=1

x

2

i

=

n



i=1

x

i

y

i

.

For example, for the timber data from Table 15.5 we would obtain

36 α + 1646.4 β = 52 901

1646.4 α + 81750.02 β = 2 790 525.

These are two equations with two unknowns α and β.Solvingforα and β

yields the solutions ˆα = −1160.5and

ˆ

β =57.51. In Figure 22.2 a scatterplot of

the timber dataset, together with the estimated regression line y = −1160.5+

57.51x,isdepicted.

Quick exercise 22.1 Suppose you are given a piece of Australian timber with

density 65. What would you choose as an estimate for the Janka hardness?

22.1 Least squares estimation and regression 331

20 30 40 50 60 70 80

Wood density

0

500

1000

1500

2000

2500

3000

3500

Hardness

.

·

Fig. 22.2. Scatterplot and estimated regression line for the timber data.

In general, writing



instead of



n

i=1

, we ﬁnd the following formulas for the

estimates ˆα (the intercept )and

ˆ

β (the slope):

ˆ

β =

n



x

i

y

i

− (



x

i

)(



y

i

)

n



x

2

i

− (



x

i

)

2

(22.1)

ˆα =¯y

n

−

ˆ

β¯x

n

. (22.2)

Since S(α, β) is an elliptic paraboloid (a “vase”), it follows that (ˆα,

ˆ

β)isthe

unique minimum of S(α, β) (except when all x

i

are equal).

Quick exercise 22.2 Check that the line y =ˆα +

ˆ

βx always passes through

the “center of gravity” (¯x

n

, ¯y

n

).

Least squares estimators are unbiased

We denote the least squares estimates by ˆα and

ˆ

β. It is quite common to also

denote the least squares estimators by ˆα and

ˆ

β:

ˆα =

¯

Y

n

−

ˆ

β¯x

n

,

ˆ

β =

n



x

i

Y

i

− (



x

i

)(



Y

i

)

n



x

2

i

− (



x

i

)

2

.

In Exercise 22.12 it is shown that

ˆ

β is an unbiased estimator for β.Usingthis

and the fact that E[Y

i

]=α + βx

i

(see page 258), we ﬁnd for ˆα:

E[ˆα]=E



¯

Y

n



− ¯x

n

E



ˆ

β



=

1

n



i=1

E[Y

i

] − ¯x

n

β

=

1

n



i=1

(α + βx

i

) − ¯x

n

β = α + β ¯x

n

− ¯x

n

β

= α.

We see that ˆα is an unbiased estimator for α.

332 22 The method of least squares

An unbiased estimator for σ

2

In the simple linear regression model the assumptions imply that the random

variables Y

i

are independent with variance σ

2

. Unfortunately, one cannot ap-

ply the usual estimator (1/(n − 1))



n

i=1



Y

i

−

¯

Y

i



2

for the variance of the

Y

i

(see Section 19.4), because diﬀerent Y

i

have diﬀerent expectations. What

would be a reasonable estimator for σ

2

? The following quick exercise suggests

a candidate.

Quick exercise 22.3 Let U

1

,U

2

,...,U

n

be independent random variables,

each with expected value zero and variance σ

2

. Show that

T =

1

n



i=1

U

2

i

is an unbiased estimator for σ

2

.

At ﬁrst sight one might be tempted to think that the unbiased estimator T

from this quick exercise is a useful tool to estimate σ

2

. Unfortunately, we only

observe the x

i

and Y

i

,nottheU

i

. However, from the fact that U

i

= Y

i

−α−βx

i

,

it seems reasonable to try

1

n



i=1

(Y

i

− ˆα −

ˆ

βx

i

)

2

(22.3)

as an estimator for σ

2

. Tedious calculations show that the expected value of

this random variable equals

n−2

n

σ

2

. But then we can easily turn it into an

unbiased estimator for σ

2

.

An unbiased estimator for σ

2

. In the simple linear regression

model the random variable

ˆσ

2

=

1

n − 2

n



i=1

(Y

i

− ˆα −

ˆ

βx

i

)

2

is an unbiased estimator for σ

2

.

22.2 Residuals

A way to explore whether the simple linear regression model is appropriate

to model a given bivariate dataset is to inspect a scatterplot of the so-called

residuals r

i

against the x

i

.Theith residual r

i

is deﬁned as the vertical distance

between the ith point and the estimated regression line:

r

i

= y

i

− ˆα −

ˆ

βx

i

,i=1, 2,...,n.

22.2 Residuals 333

When a linear model is appropriate, the scatterplot of the residuals r

i

against

the x

i

should show truly random ﬂuctuations around zero, in the sense that

it should not exhibit any trend or pattern. This seems to be the case in

Figure 22.3, which shows the residuals for the black cherry tree data from

Exercise 17.9.

02468

−0.15

−0.10

−0.05

0.00

0.05

0.10

0.15

Residual

·

Fig. 22.3. Scatterplot of r

i

versus x

i

for the black cherry tree data.

Quick exercise 22.4 Recall from Quick exercise 22.2 that (¯x

n

, ¯y

n

)isonthe

regression line y =ˆα +

ˆ

βx, i.e., that ¯y

n

=ˆα +

ˆ

β¯x

n

. Use this to show that



n

i=1

r

i

= 0, i.e., that the sum of the residuals is zero.

In Figure 22.4 we depicted r

i

versus x

i

for the timber dataset. In this case a

slight parabolic pattern can be observed. Figures 22.2 and 22.4 suggest that

20 30 40 50 60 70

−400

−200

0

200

400

600

800

Residual

·

Fig. 22.4. Scatterplot of r

i

versus x

i

for the timber data with the simple linear

regression model Y

i

= α + βx

i

+ U

i

.

334 22 The method of least squares

for the timber dataset a better model might be

Y

i

= α + βx

i

+ γx

2

i

+ U

i

for i =1, 2,...,n.

In this new model the residuals are

r

i

= y

i

− ˆα −

ˆ

βx

i

− ˆγx

2

i

,

where ˆα,

ˆ

β,andˆγ are the least squares estimates obtained by minimizing

n



i=1



y

i

− α − βx

i

− γx

2

i



2

.

In Figure 22.5 we depicted r

i

versus x

i

. The residuals display no trend or

pattern, except that they “fan out”—an example of a phenomenon called

heteroscedasticity.

20 30 40 50 60 70

−400

−200

0

200

400

600

800

Residual

·

Fig. 22.5. Scatterplot of r

i

versus x

i

for the timber data with the model Y

i

=

α + βx

i

+ γx

2

i

+ U

i

.

Heteroscedasticity

The assumption of equal variance of the U

i

(and therefore of the Y

i

) is called

homoscedasticity. In case the variance of Y

i

depends on the value of x

i

,we

speak of heteroscedasticity. For instance, heteroscedasticity occurs when Y

i

with a large expected value have a larger variance than those with small ex-

pected values. This produces a “fanning out” eﬀect, which can be observed

in Figure 22.5. This ﬁgure strongly suggests that the timber data are het-

eroscedastic. Possible ways out of this problem are a technique called weighted

least squares or the use of variance-stabilizing transformations.

22.3 Relation with maximum likelihood 335

22.3 Relation with maximum likelihood

To apply the method of least squares no assumption is needed about the type

of distribution of the U

i

. In case the type of distribution of the U

i

is known,

the maximum likelihood principle can be applied. Consider, for instance, the

classical situation where the U

i

are independent with an N(0,σ

2

) distribution.

What are the maximum likelihood estimates for α and β?

In this case the Y

i

are independent, and Y

i

has an N(α+βx

i

,σ

2

) distribution.

Under these assumptions and assuming that the linear model is appropriate

to model a given bivariate dataset, the r

i

should look like the realization of a

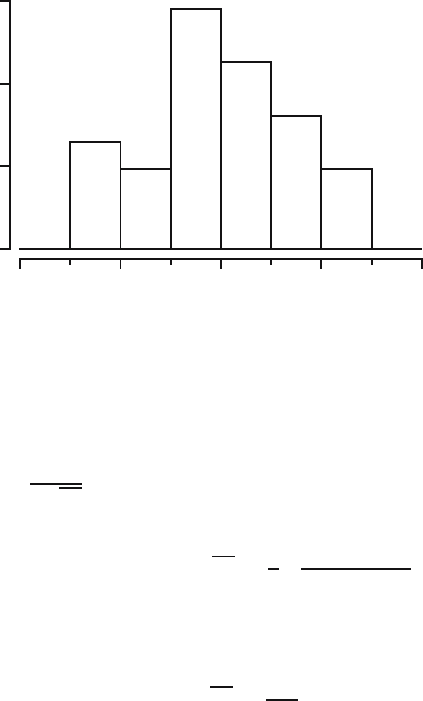
random sample from a normal distribution. As an example a histogram of the

residuals r

i

of the cherry tree data of Exercise 17.9 is depicted in Figure 22.6.

−0.2 −0.1 0.0 0.1 0.2

0

2

4

6

Fig. 22.6. Histogram of the residuals r

i

for the black cherry tree data.

The data do not exhibit strong evidence against the assumption of normality.

When Y

i

has an N(α + βx

i

,σ

2

) distribution, the probability density of Y

i

is

given by

f

i

(y)=

1

σ

√

2π

e

−(y−α−βx

i

)

2

/(2σ

2

)

for −∞<y<∞.

Since

ln (f

i

(y

i

)) = −ln(σ) − ln(

√

2π) −

1

2



y

i

− α − βx

i

σ



2

,

the loglikelihood is:

(α, β, σ)=ln(f

1

(y

1

)) + ···+ln(f

n

(y

n

))

= −n ln(σ) − n ln(

√

2π) −

1

2σ

2

n



i=1

(y

i

− α − βx

i

)

2

.

A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику - Как? и Почему? )

Подождите немного. Документ загружается.