A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику - Как? и Почему? )
Подождите немного. Документ загружается.


336 22 The method of least squares
Note that for any fixed σ>0, the loglikelihood (α, β, σ) attains its maximum
precisely when
n
i=1
(y
i
− α − βx
i
)
2
is minimal. Hence, in case the U
i
are
independent with an N(0,σ
2
) distribution, the maximum likelihood principle
and the least squares method yield the same estimators.
To find the maximum likelihood estimate of σ we differentiate (α, β, σ)with
respect to σ:
∂
∂σ
(α, β, σ)=−
n
σ
+
1
σ
3
n
i=1
(y
i
− α − βx
i
)
2
.
It follows (from the invariance principle on page 321) that the maximum
likelihood estimator of σ
2
is given by
1
n
n
i=1
(Y
i
− ˆα −
ˆ
βx
i
)
2
,
which is the estimator from (22.3).
22.4 Solutions to the quick exercises
22.1 We can use the estimated regression line y = −1160.5+57.51x to predict
the Janka hardness. For density x = 65 we find as a prediction for the Janka
hardness y = 2577.65.
22.2 Rewriting ˆα =¯y
n
−
ˆ
β, it follows that ¯y
n
=ˆα +
ˆ
β¯x
n
, which means that
(¯x
n
, ¯y
n
) is a point on the estimated regression line y =ˆα +
ˆ
βx.
22.3 We need to show that E[T ]=σ
2
.SinceE[U
i
]=0,Var(U
i
)=E
U
2
i
,
so that:
E[T ]=E
%
1
n
n
i=1
U
2
i
&
=
1
n
n
i=1
E
U
2
i
=
1
n
n
i=1
Var(U
i
)=σ
2
.
22.4 Since r
i
= y
i
− (ˆα +
ˆ
βx
i
)fori =1, 2,...,n, it follows that the sum of
the residuals equals
r
i
=
y
i
−
nˆα +
ˆ
β
x
i
= n¯y
n
−
nˆα + n
ˆ
β¯x
n
= n
¯y
n
− (ˆα +
ˆ
β¯x
n
)
=0,
because ¯y
n
=ˆα +
ˆ
β¯x
n
, according to Quick exercise 22.2.

22.5 Exercises 337
22.5 Exercises
22.1 Consider the following bivariate dataset:
(1, 2) (3, 1.8) (5, 1).
a. Determine the least squares estimates ˆα and
ˆ
β of the parameters of the
regression line y = α + βx.
b. Determine the residuals r
1
,r
2
,andr
3
and check that they add up to 0.
c. Draw in one figure the scatterplot of the data and the estimated regression
line y =ˆα +
ˆ
βx.
22.2 Adding one point may dramatically change the estimates of α and β.
Suppose one extra datapoint is added to the dataset of the previous exercise
and that we have as dataset:
(0, 0) (1, 2) (3, 1.8) (5, 1).
Determine the least squares estimate of
ˆ
β.Apointsuchas(0, 0), which dra-
matically changes the estimates for α and β, is called a leverage point.
22.3 Suppose we have the following bivariate dataset:
(1, 3.1) (1.7, 3.9) (2.1, 3.8) (2.5, 4.7) (2.7, 4.5).
a. Determine the least squares estimates ˆα and
ˆ
β of the parameters of the
regression line y = α + βx. You may use that
x
i
= 10,
y
i
= 20,
x
2
i
=21.84, and
x
i
y
i
=41.61.
b. Draw in one figure the scatterplot of the data and the estimated regression
line y =ˆα +
ˆ
βx.
22.4 We are given a bivariate dataset (x
1
,y
1
), (x
2
,y
2
),...,(x
100
,y
100
). For
this bivariate dataset it is known that
x
i
= 231.7,
x
2
i
= 2400.8,
y
i
=
321, and
x
i
y
i
= 5189. What are the least squares estimates ˆα and
ˆ
β of the
parameters of the regression line y = α + βx?
22.5 For the timber dataset it seems reasonable to leave out the intercept α
(“no hardness without density”). The model then becomes
Y
i
= βx
i
+ U
i
for i =1, 2,...,n.
Show that the least squares estimator
ˆ
β of β is now given by
ˆ
β =
n
i=1
x
i
Y
i
n
i=1
x
2
i
by minimizing the appropriate sum of squares.
338 22 The method of least squares
22.6 (Quick exercise 22.1 and Exercise 22.5 continued). Suppose we are
given a piece of Australian timber with density 65. What would you choose
as an estimate for the Janka hardness, based on the regression model with
no intercept? Recall that
x
i
y
i
= 2790525 and
x
2
i
= 81750.02 (see also
Section 22.1).
22.7 Consider the dataset
(x
1
,y
1
), (x
2
,y
2
),...,(x
n
,y
n
),
where x
1
,x
2
,...,x
n
are nonrandom and y
1
,y
2
,...,y
n
are realizations of ran-
dom variables Y
1
,Y
2
,...,Y
n
, satisfying
Y
i
=e
α+βx
i
+ U
i
for i =1, 2,...,n.
Here U
1
,U
2
,...,U
n
are independent random variables with zero expectation
and variance σ
2
. What are the least squares estimates for the parameters α
and β in this model?
22.8 Which simple regression model has the larger residual sum of squares
n
i=1
r
2
i
, the model with intercept or the one without?
22.9 For some datasets it seems reasonable to leave out the slope β.For
example, in the jury example from Section 6.3 it was assumed that the score
that juror i assigns when the performance deserves a score g is Y
i
= g + Z
i
,
where Z
i
is a random variable with values around zero. In general, when the
slope β is left out, the model becomes
Y
i
= α + U
i
for i =1, 2,...,n.
Show that
¯
Y
n
is the least squares estimator ˆα of α.
22.10 In the method of least squares we choose α and β in such a way
that the sum of squared residuals S(α, β) is minimal. Since the ith term in
this sum is the squared vertical distance from (x
i
,y
i
) to the regression line
y = α + βx, one might also wonder whether it is a good idea to replace this
squared distance simply by the distance. So, given a bivariate dataset
(x
1
,y
1
), (x
2
,y
2
),...,(x
n
,y
n
),
choose α and β in such a way that the sum
A(α, β)=
n
i=1
|y
i
− α − βx
i
|
is minimal. We will investigate this by a simple example. Consider the follow-
ing bivariate dataset:
(0, 2), (1, 2), (2, 0).
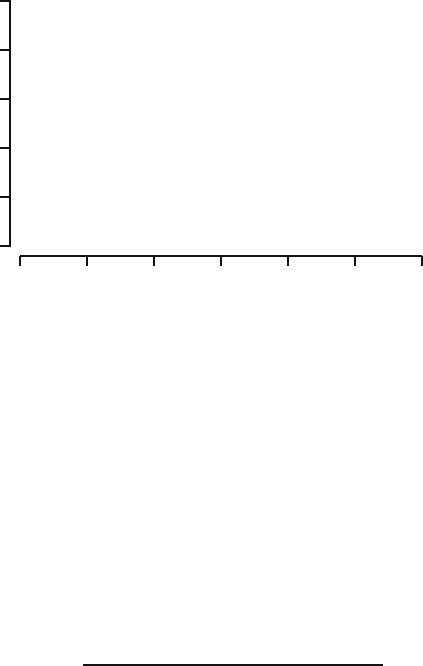
22.5 Exercises 339
a. Determine the least squares estimates ˆα and
ˆ
β, and draw in one figure
the scatterplot of the data and the estimated regression line y =ˆα +
ˆ
βx.
Finally, determine A(ˆα,
ˆ
β).
b. One might wonder whether ˆα and
ˆ
β also minimize A(α, β). To investigate
this, choose β = − 1 and find α’s for which A(α, −1) <A(ˆα,
ˆ
β). For which
α is A(α, −1) minimal?
c. Find α and β for which A(α, β) is minimal.
22.11 Consider the dataset (x
1
,y
1
), (x
2
,y
2
),...,(x
n
,y
n
), where the x
i
are
nonrandom and the y
i
are realizations of random variables Y
1
,Y
2
,...,Y
n
sat-
isfying
Y
i
= g(x
i
)+U
i
for i =1, 2,...,n,
where U
1
,U
2
,...,U
n
are independent random variables with zero expecta-
tion and variance σ
2
. Visual inspection of the scatterplot of our dataset in
20 30 40 50 60 70 80
0
500
1000
1500
2000
2500
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
Fig. 22.7. Scatterplot of y
i
versus x
i
.
Figure 22.7 suggests that we should model the Y
i
by
Y
i
= βx
i
+ γx
2
i
+ U
i
for i =1, 2,...,n.
a. Show that the least squares estimators
ˆ
β and ˆγ satisfy
β
x
2
i
+ γ
x
3
i
=
x
i
y
i
,
β
x
3
i
+ γ
x
4
i
=
x
2
i
y
i
.
b. Infer from a—for instance, by using linear algebra—that the estimators
ˆ
β and ˆγ are given by
ˆ
β =
(
x
i
Y
i
)(
x
4
i
) − (
x
3
i
)(
x
2
i
Y
i
)
(
x
2
i
)(
x
4
i
) − (
x
3
i
)
2
340 22 The method of least squares
and
ˆγ =
(
x
2
i
)(
x
2
i
Y
i
) − (
x
3
i
)(
x
i
Y
i
)
(
x
2
i
)(
x
4
i
) − (
x
3
i
)
2
.
22.12 The least square estimator
ˆ
β from (22.1) is an unbiased estimator
for β. You can show this in four steps.
a. First show that
E
ˆ
β
=
n
x
i
E[Y
i
] − (
x
i
)(
E[Y
i
])
n
x
2
i
− (
x
i
)
2
.
b. Next use that E [Y
i
]=α + βx
i
, to obtain that
E
ˆ
β
=
n
x
i
(α + βx
i
) − (
x
i
)[nα + β
x
i
]
n
x
2
i
− (
x
i
)
2
.
c. Simplify this last expression to find
E
ˆ
β
=
nα
x
i
+ nβ
x
2
i
− nα
x
i
− β(
x
i
)
2
n
x
2
i
− (
x
i
)
2
.
d. Finally, conclude that
ˆ
β is an unbiased estimator for β.

23
Confidence intervals for the mean
Sometimes, a range of plausible values for an unknown parameter is preferred
to a single estimate. We shall discuss how to turn data into what are called
confidence intervals and show that this can be done in such a manner that
definite statements can be made about how confident we are that the true pa-
rameter value is in the reported interval. This level of confidence is something
you can choose. We start this chapter with the general principle of confidence
intervals. We continue with confidence intervals for the mean, the common
way to refer to confidence intervals made for the expected value of the model
distribution. Depending on the situation, one of the four methods presented
will apply.
23.1 General principle
In previous chapters we have encountered sample statistics as estimators for
distribution features. This started somewhat informally in Chapter 17, where
it was claimed, for example, that the sample mean and the sample variance
are usually close to µ and σ
2
of the underlying distribution. Bias and MSE
of estimators, discussed in Chapters 19 and 20, are used to judge the quality
of estimators. If we have at our disposal an estimator T for an unknown
parameter θ, we use its realization t as our estimate for θ. For example, when
collecting data on the speed of light, as Michelson did (see Section 13.1), the
unknown speed of light would be the parameter θ, our estimator T could
be the sample mean, and Michelson’s data then yield an estimate t for θ of
299 852.4 km/sec. We call this number a point estimate: if we are required
to select one number, this is it. Had the measurements started a day earlier,
however, the whole experiment would in essence be the same, but the results
might have been different. Hence, we cannot say that the estimate equals the
speed of light but rather that it is close to the true speed of light. For example,
we could say something like: “we have great confidence that the true speed of

342 23 Confidence intervals for the mean
light is somewhere between . . . and . . . .” In addition to providing an interval
of plausible values for θ we would want to add a specific statement about how
confident we are that the true θ is among them.
In this chapter we shall present methods to make confidence statements about
unknown parameters, based on knowledge of the sampling distributions of cor-
responding estimators. To illustrate the main idea, suppose the estimator T
is unbiased for the speed of light θ. For the moment, also suppose that T
has standard deviation σ
T
= 100 km/sec (we shall drop this unrealistic as-
sumption shortly). Then, applying formula (13.1), which was derived from
Chebyshev’s inequality (see Section 13.2), we find
P(|T − θ| < 2σ
T
) ≥
3
4
. (23.1)
In words this reads: with probability at least 75%, the estimator T is within
2σ
T
= 200 of the true speed of light θ. We could rephrase this as
T ∈ (θ − 200,θ+ 200) with probability at least 75%.
However, if I am near the city of Paris, then the city of Paris is near me: the
statement “T is within 200 of θ”isthesameas“θ is within 200 of T ,” and
we could equally well rephrase (23.1) as
θ ∈ (T − 200,T+ 200) with probability at least 75%.
Note that of the last two equations the first is a statement about a random
variable T being in a fixed interval, whereas in the second equation the interval
is random and the statement is about the probability that the random interval
covers the fixed but unknown θ.Theinterval(T −200,T+ 200) is sometimes
called an interval estimator, and its realization is an interval estimate.
Evaluating T for the Michelson data we find as its realization t = 299 852.4,
and this yields the statement
θ ∈ (299 652.4, 300 052.4). (23.2)
Because we substituted the realization for the random variable, we cannot
claim that (23.2) holds with probability at least 75%: either the true speed of
light θ belongs to the interval or it does not; the statement we make is either
true or false, we just do not know which. However, because the procedure
guarantees a probability of at least 75% of getting a “right” statement, we
say:
θ ∈ (299 652.4, 300 052.4) with confidence at least 75%. (23.3)
The construction of this confidence interval only involved an unbiased estima-
tor and knowledge of its standard deviation. When more information on the
sampling distribution of the estimator is available, more refined statements
can be made, as we shall see shortly.

23.1 General principle 343
Quick exercise 23.1 Repeat the preceding derivation, starting from the
statement P(|T − θ| < 3σ
T
) ≥ 8/9 (check that this follows from Chebyshev’s
inequality). What is the resulting confidence interval for the speed of light,
and what is the corresponding confidence?
A general definition
Many confidence intervals are of the form
1
(t − c · σ
T
,t+ c · σ
T
)
we just encountered, where c is a number near 2 or 3. The corresponding
confidence is often much higher than in the preceding example. Because there
are many other ways confidence intervals can (or have to) be constructed, the
general definition looks a bit different.
Confidence intervals. Suppose a dataset x
1
,...,x
n
is given,
modeled as realization of random variables X
1
,...,X
n
.Letθ be the
parameter of interest, and γ a number between 0 and 1. If there exist
sample statistics L
n
= g(X
1
,...,X
n
)andU
n
= h(X
1
,...,X
n
)such
that
P(L
n
<θ<U
n
)=γ
for every value of θ,then
(l
n
,u
n
),
where l
n
= g(x
1
,...,x
n
)andu
n
= h(x
1
,...,x
n
), is called a 100γ%
confidence interval for θ.Thenumberγ is called the confidence level.
Sometimes sample statistics L
n
and U
n
as required in the definition do not
exist, but one can find L
n
and U
n
that satisfy
P(L
n
<θ<U
n
) ≥ γ.
The resulting confidence interval (l
n
,u
n
) is called a conservative 100γ% confi-
dence interval for θ: the actual confidence level might be higher. For example,
the interval in (23.2) is a conservative 75% confidence interval.
Quick exercise 23.2 Why is the interval in (23.2) a conservative 75% con-
fidence interval?
There is no way of knowing whether an individual confidence interval is cor-
rect, in the sense that it indeed does cover θ. The procedure guarantees that
each time we make a confidence interval we have probability γ of covering θ.
What this means in practice can easily be illustrated with an example, using
simulation:
1
Another form is, for example, (c
1
t, c
2
t).
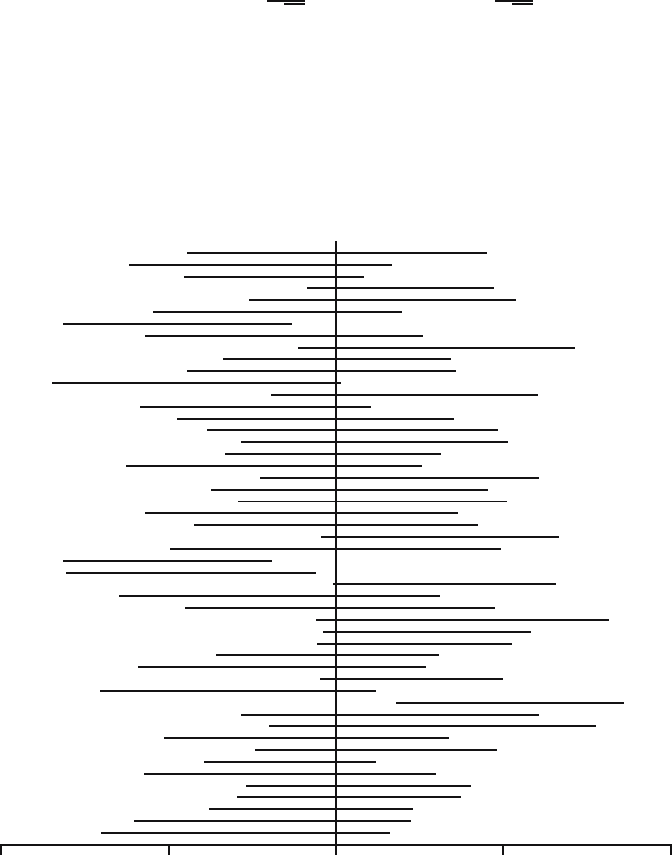
344 23 Confidence intervals for the mean
Generate x
1
,...,x
20
from an N(0, 1) distribution. Next, pretend that
it is known that the data are from a normal distribution but that both
µ and σ are unknown. Construct the 90% confidence interval for the
expectation µ using the method described in the next section, which
says to use (l
n
,u
n
)with
l
n
=¯x
20
− 1.729
s
20
√
20
u
n
=¯x
20
+1.729
s
20
√
20
,
where ¯x
20
and s
20
are the sample mean and standard deviation. Fi-
nally, check whether the “true µ,” in this case 0, is in the confidence
interval.
We repeated the whole procedure 50 times, making 50 confidence intervals
for µ. Each confidence interval is based on a fresh independently generated
set of data. The 50 intervals are plotted in Figure 23.1 as horizontal line
−1 1µ
Fig. 23.1. Fifty 90% confidence intervals for µ =0.
23.2 Normal data 345
segments, and at µ (0!) a vertical line is drawn. We count 46 “hits”: only four
intervals do not contain the true µ.
Quick exercise 23.3 Suppose you were to make 40 confidence intervals with
confidence level 95%. About how many of them should you expect to be
“wrong”? Should you be surprised if 10 of them are wrong?
In the remainder of this chapter we consider confidence intervals for the mean :
confidence intervals for the unknown expectation µ of the distribution from
which the sample originates. We start with the situation where it is known that
the data originate from a normal distribution, first with known variance, then
with unknown variance. Then we drop the normal assumption, first use the
bootstrap, and finally show how, for very large samples, confidence intervals
based on the central limit theorem are made.
23.2 Normal data
Suppose the data can be seen as the realization of a sample X
1
,...,X
n
from
an N (µ, σ
2
) distribution and µ is the (unknown) parameter of interest. If the
variance σ
2
is known, confidence intervals are easily derived. Before we do
this, some preparation has to be done.
Critical values
We shall need so-called critical values for the standard normal distribution.
The critical value z
p
of an N (0, 1) distribution is the number that has right
tail probability p. It is defined by
P(Z ≥ z
p
)=p,
where Z is an N(0, 1) random variable. For example, from Table B.1 we read
P(Z ≥ 1.96) = 0.025, so z
0.025
=1.96. In fact, z
p
is the (1 − p)th quantile of
the standard normal distribution:
Φ(z
p
)=P(Z ≤ z
p
)=1− p.
By the symmetry of the standard normal density, P(Z ≤−z
p
)=P(Z ≥ z
p
)=
p,soP(Z ≥−z
p
)=1− p and therefore
z
1−p
= −z
p
.
For example, z
0.975
= −z
0.025
= −1.96. All this is illustrated in Figure 23.2.
Quick exercise 23.4 Determine z
0.01
and z
0.95
from Table B.1.
